基于频带熵的滚动轴承故障诊断研究

刘 韬， 陈 进， 董广明

(上海交通大学 机械系统与振动国家重点实验室，上海 200240)

轴承是旋转设备的重要部件，其故障是造成旋转机械故障的主要原因之一。因此，对轴承的状态监测与故障诊断一直是机械设备故障诊断的研究热点[1]。

故障诊断的关键在于从原始信号中提取故障特征信号，基于振动信号分析方法已被广泛应用到轴承的故障诊断领域。但由于轴承信号的非平稳性，传统的时域和频域分析方法常受到限制。时频分析是一种比较有效的非平稳信号分析方法，它能建立信号能量在时间和频率上的分布[2]，并通过对时频分析的后续处理，为故障诊断提供依据。Antoni等[3]将时域的峭度指标与短时傅里叶变换(STFT)相结合，提出了一种基于谱峭度的轴承故障诊断方法。Qu等[4]将信息熵引入频谱分析，并将谱熵应用于的设备故障诊断。于德介等[5]将EMD方法与时频熵结合，并将其用于齿轮的故障诊断。

当滚动轴承发生故障时，其振动信号往往表现为一种幅值调制特性[6]，通过包络分析就可以得到轴承的故障特征频率，从而实现对轴承的故障诊断。由于在实际的故障诊断过程中，信号通常伴随着比较大的背景噪声，因此需选取信噪比较高或受其它干扰较小的频带来进行解包络。本文结合信息熵和振动信号的时频分布特点，提出了一种基于频带熵的包络解调方法，利用轴承共振频率处频带熵较小的特点，详细讨论了自适应滤波器相关参数的设计方法。最后通过实验验证了所提出方法在轴承故障进行诊断中的可行性与有效性。

1 理论基础

1.1 短时傅里叶变换

频带熵表征的是每个频率成分随时间的变化情况。为了计算频带熵，需要先得到信号的时频分布，本文采用的是STFT方法。假定已知时域信号x(t)，则STFT可以被定义为：

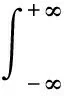
(1)

其中，ω(t-τ)是中心位于τ的窗函数，其宽度越小则时域分辨率越好，通常取汉宁窗；由于ejωt是δ函数，也可较好的保持频率分辨率。

1.2 幅值谱熵

频带熵定义了单一频率成分随时间变化的复杂度指标。而传统的幅值谱熵表达了信号频率的复杂度情况，假定信号x(t)的幅值谱是X(i),i=1,2,…,N，那么归一化后的幅值谱熵可以被定义为：

(2)

其中，Hs是信号的幅值谱熵。pi定义了第i个频率分量在全频段中的幅值比例，并且P={p1,p2,…,pN}只取决于信号幅值的分布。当信号能量集中在单一频率时，幅值谱熵最小；信号成分越复杂，即信号能量分布在众多频率下时，幅值谱熵就越大，因此Hs取值在[0,1]之间[7]。

1.3 频带熵

幅值谱熵定义了一段时间内信号频率成分的复杂度，但是却不能反映这段时间内，各个频率分量随时间的变化情况。因此，结合时频分析，提出了基于幅值谱熵的频带熵分析方法，其计算过程如下：

首先，对信号做时频变换，本文采用STFT实现。对原信号x(i),i=1,2,…,N，STFT后时频分布为：

(3)

其中，M是频率点数，C=N/L，L是窗函数沿时间轴移动的步长。

其次，第i个频率分量的幅值沿时间的变化可以被定义为Xfi=(ri,1，ri,2，…,ri,C)，则单个频率分量的频带熵可以由式(4)估计得到：

(4)

其中，F是频率分量Xfi沿时间轴的谱分布，其变化揭示了该频率分量沿时间轴的变化情况。

最后，通过计算每个频率分量的频带熵值，就可以得到全频带的各个频率分量的频带熵分布：

Hsf=(Hs1,Hs2,…,HsM)

(5)

如果频率分量Xfi随时间的变化平缓或是规律地存在于信号中，则该频率分量的频带熵值较小；如果在一段时间内有复杂的波动，则频带熵值则较大。该特性可以被用于旋转设备的故障诊断，例如在轴承故障诊断中用于寻找轴承的共振频率[8]，也就是频带熵值最小处的频率分量(H=min(Hsf))，从而为自适应滤波器的设计提供参考。在滤波器设计时，由于中心频率与计算频带熵的STFT窗长度有关，因此可以通过计算不同窗长度下的频带熵值，并取熵最小时的中心频率值f0和窗长度Nw来设计滤波器。

1.4 基于频带熵的包络谱分析

在得到轴承的各个频率分量的频带熵值后，首先利用频带熵方法设计滤波器，然后就可以对滤波后的信号利用包络解调方法获取轴承的故障特征频率，从而实现轴承的故障诊断，具体步骤如下：

首先是按照式(1)～式(5)计算不同窗长度下的频带熵值，其中窗长度Nw=2k,k=1,2,…,M。

其次是设计带通滤波器。选择频带熵值最小处对应的频率分量作为滤波器的中心频率f0，并利用STFT的窗长度Nw估计滤波器的带宽Δf。滤波器带宽可选Δf≈1.5fs/Nw，fs是信号的采样频率[9]。

最后，利用获得的滤波器参数设计带通滤波器。然后对滤波后的信号利用包络解调方法提取低频的轴承故障频率。本文使用基于Hilbert变换的包络解调方法[10]，信号x(t)的包络信号可以被定义为：

(6)

其中，h(t)是信号的Hilbert变换，它可以被视为是一个单位幅值全通滤波器，并且滤波后相移为±90°，相移仅与频率正负有关。构造信号E(t)的频谱就是原信号x(t)的包络谱。

2 仿真分析

首先我们利用滚动轴承仿真信号来详细讨论频带熵与滤波器的参数的关系，并确定设计方案。根据公式(7)可得到滚动轴承仿真信号。其中，Ai表示第i次冲击的幅值，B是系统衰减阻尼比，n(i)为噪声：

(7)

设置系统的采样频率fs为12 000 Hz，结构共振频率fn为3 000 Hz，故障频率fm为79 Hz，转频fr为28 Hz，阻尼比B为400。为了说明方法的适用性，添加信噪比为-5 dB的背景噪声。仿真的轴承故障信号如图1(a)所示。从图1(b)的直接包络谱可以看到，由于噪声的影响，并不能清晰的得到轴承的故障频率。图1(c)是信号的功率谱，虽然在3 000 Hz左右信号的共振频率处有较强的峰值，但是却不能得到轴承的特征频率。

图1 内圈故障仿真信号

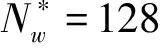
图3是轴承故障信号滤波后的时域波形图，以及包络谱。可以看到，滤波后的包络谱能够明显的识别出轴承的故障信号，其中，fr=28.13 Hz，fi=78.52 Hz，与仿真信号的转频和故障频率一致。

3 实验验证

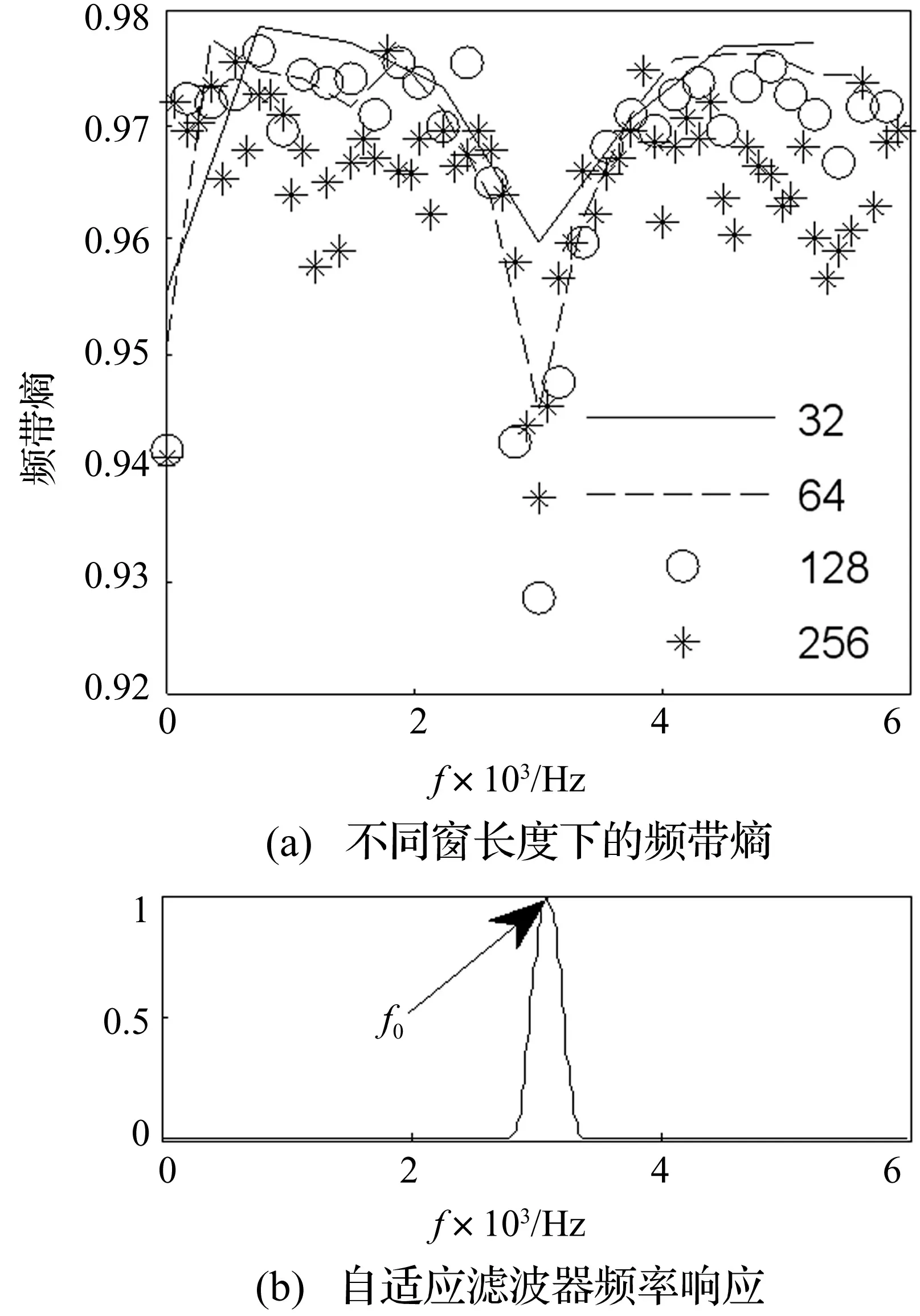
图2 信号的频带熵及滤波器频率响应

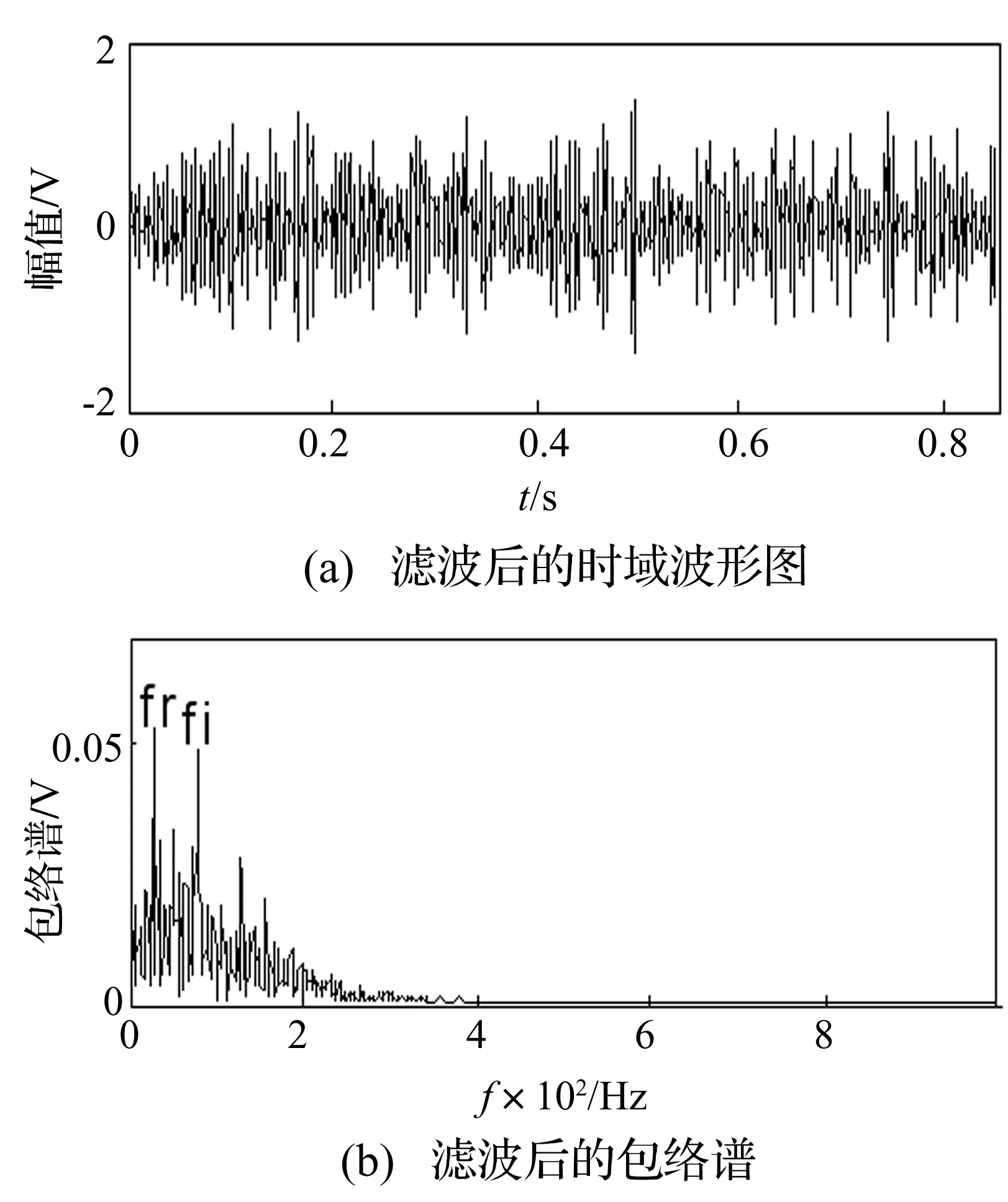
图3 滤波后的时域波形图和包络谱

为了验证频带熵方法在实际轴承故障诊断中的应用价值，设计了如下实验：实验装置如图4所示，试验轴承安装在转轴上，内圈随转轴被转子驱动设备驱动，转速是720 r/min，外圈被装夹装置固定，轴承振动信号被加速度传感器获取，然后通过NI 9234数据采集卡采集振动信号，采集程序使用NI LabVIEW编写。两个通道数据的采样频率都是25.6 kHz。实验一共采集了30组数据，每一组数据的时长是0.8 s。实验轴承的型号是GB6203深沟球轴承，并通过电火花在轴承外圈内表面加工得到了外圈点蚀故障。振动噪声主要是源于电机和转子驱动设备的振动，以及滚动体相对于滚道的相对滑动。由于加工的外圈点蚀故障程度较小，相对于实验时的背景噪声(包括实验环境，条件及测量系统的背景噪音)，其故障特征能量较弱，因此实验数据信噪比较低，轴承的特征频率也难以直接通过包络分析得到。

图4 实验设备安装图

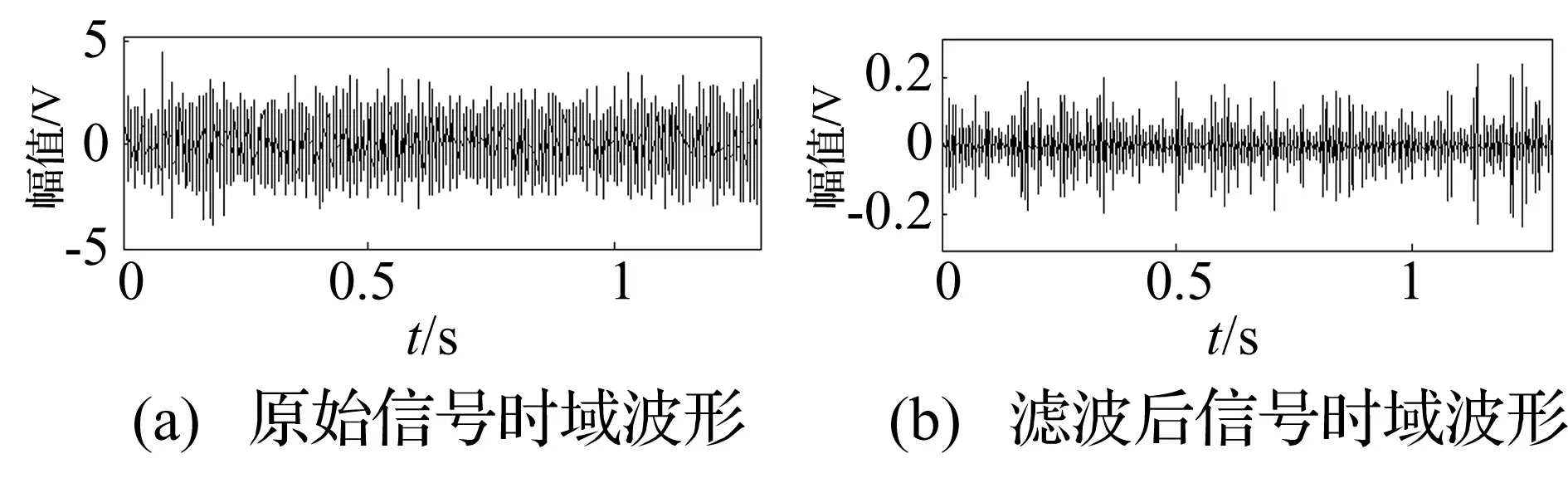
图5 滤波前和滤波后的时域波形图

图6 滤波前和滤波后的信号包络谱

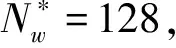
4 结 论

本文在时频分析和信息熵的基础上，提出了频带熵方法并将其用于滚动轴承的故障诊断。详细讨论了频带熵对单一频率成分随时间变化的表征能力。利用该特性实现了自适应带通滤波器最优参数设计，并分析了频带熵与滤波中心频率、窗长度和采样频率的关系。通过将该滤波方法与包络分析结合，实现了强背景噪声条件下对轴承故障特征频率的提取。最后通过仿真和实验验证了提出方法的可行性与有效性。

参 考 文 献

[1]Jardine A K S, Lin D,Banjevic D. A review on machinery diagnostics and prognostics implementing condition-based maintenance[J]. Mechanical Systems and Signal Processing, 2006,20(7)：1483-1510.

[2]Dong G M,Chen J, Noise resistant time frequency analysis and application in fault diagnosis of rolling element bearings [J]. Mechanical Systems and Signal Processing, 2012,33：212-236.

[3]Antoni J, Randall R B, The spectral kurtosis：Application to the vibratory surveillance and diagnostics of rotating machines [J]. Mechanical Systems and Signal Processing, 2006, 20(2)：308-331.

[4]Qu L S, Li L M, Lee J, Enhanced diagnostic certainty using information entropy theory [J]. Advanced Engineering Informatics, 2003, 17(3-4)：141-150.

[5]于德介，张 嵬，程军圣，等. 基于EMD的时频熵在齿轮故障诊断中的应用[J]. 振动与冲击，2005,24(5)：26-27.

YU De-jie, ZHANG Wei, CHENG Jun-sheng,et al. Application of time-frequency entropy to gear fault diagnosis on EMD [J]. Journal of Vibration and Shock, 2005, 24(5)：26-27.

[6]McFadden P D, Smith J D, Model for the vibration produced by a single point defect in a rolling element bearing [J]. Journal of Sound and Vibration, 1984, 96(1)：69-82.

[7]Pan Y N, Chen J, Li X L. Spectral entropy:A complementary index for rolling element bearing performance degradation assessment [J]. Journal of Mechanical Engineering System, 2009, 223(5)：1223-1231.

[8]Antoni J, Cyclic spectral analysis of rolling-element bearing signals：Facts and fictions [J]. Journal of Sound and Vibration, 2007, 304(3-5)：497-529.

[9]Sawalhi N, Randall R B, Endo H.The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis [J]. Mechanical Systems and Signal Processing, 2007, 21(6)：2616-2633.

[10]Ho D, Randal R B. Optimisation of bearing diagnostic techniques using simulated and actual bearing fault signals [J]. Mechanical Systems and Signal Processing, 2000,14(5)：763-788.