金属材料表面静摩擦学特性的预测研究
——实验佐证
田红亮, 刘芙蓉, 赵春华, 方子帆, 朱大林, 陈保家, 秦红玲, 张发军
(1. 三峡大学 机械与材料学院,湖北 宜昌 443002;2. 三峡大学 水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443002)
一个零件各处的截面特性(包括截面形状、大小及材质)可以是相同的,如等截面轴;各部分截面的特性也可能不同,如台阶轴。等截面轴的零件由一个元件组成。台阶轴零件由多个元件组成,各个元件的连接部位称为刚性结合面,两相邻元件在刚性结合面无相对位移。一台机器由众多零件组成,零件与零件之间的连接部位称为柔性结合面。
摩擦学的研究对于国民经济具有重要意义,摩擦导致的磨损是机械设备失效的主要原因,大约有80%的损坏零件是由于各种形式的磨损引起的。所以在机械结构中,研究和预测柔性结合面静摩擦学特性是非常重要的。传统的Coulomb摩擦第一定律[1-3]认为,摩擦力和法向载荷成正比,静摩擦系数和所施加的法向载荷无关,亦不依赖于切向载荷,只随接触材料的不同而变化。但是随着现代摩擦学的发展,发现Coulomb摩擦第一定律中摩擦力和法向载荷不成正比;静摩擦系数对于同种材料不变的结论不适合实际工程;静摩擦系数随着接触正压力的增大而增大等。
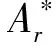
文献[1]改进分形几何理论,探究金属材料表面最大静摩擦力的来源机理,建立法向总载荷、最大静摩擦力、静摩擦系数的改进分形模型,经过数值模拟,预测静摩擦学特性,其结论和一些传统摩擦学观点迥然不同,分析产生不同的原因。但文献[1]给出的接触面积分别与分形维数及载荷的关系等,都还缺少足够的实验佐证。本文根据整个柔性结合面的结构函数,给出识别柔性结合面分形维数、分形粗糙度的理论及实验方法,对文献[1]静摩擦系数的理论解进行定量实验佐证。
1 采用修正分形理论的金属表面静摩擦模型
1.1 分形几何理论的修正
处处连续、统计学自仿射特性、点点不可微的Weierstrass-Mandelbrot函数为:
(1)
式中:G为分形粗糙度;D为分形维数;n1为最低频率的初始项,且γn1=1/L不同于文献[15]的γn1=11L(L为取样长度);γ为谱密度的尺度参数;x为表面的取样长度坐标。
应当指出式(1)截然不同于文献[15]的式(5)。
自然海岸线的特点是将小尺度下的粗糙度在所有方向上放大相同倍数后,其概率分布与大尺度下的一致,这种曲线具有统计自相似特性。但是,绝大多数实际曲线并不具有统计自相似特性,而是具有统计自仿射特性,即要使较小尺度下的概率分布与较大尺度下的一致,就必须在不同方向上放大不同的倍数,典型的例子是分子的布朗运动曲线。因此,要方便地计算统计自仿射曲线的分形维数D、分形粗糙度G,就必须采用特殊方法。
Mandelbrot发现海洋面岛屿的面积分布有幂函数规律:
(2)
式中:Nr为面积A大于面积a的岛屿之总数;F′为待定未知数;a为一个岛屿的面积。
应当指出式(2)不同于文献[15]的式(19)。
许多工程表面形貌的轮廓线都具有统计自仿射分形特性。若将粗糙表面(如金属加工表面)放大到适当尺寸,就会发现类似于地球表面的高山峡谷,用一理想平面水平切取该表面形成的接触点,也类似于海岸面的岛屿。因此,假设平面与粗糙表面接触时接触点面积的分布规律与海洋面岛屿面积的分布规律相同,即接触点的数目见式(2)。但工程表面形貌的轮廓线与岛屿的海洋线不同的是,前者接触点的轮廓曲线不是统计自相似曲线,而是统计自仿射曲线。
假设最大的微凸体接触点面积为aL,数量为1个,将此假设条件代入式(2)得:
(3)
(4)
将式(4)代入式(2)可得连续随机变量a的概率分布函数为:
(5)
连续随机变量a的概率分布密度为:
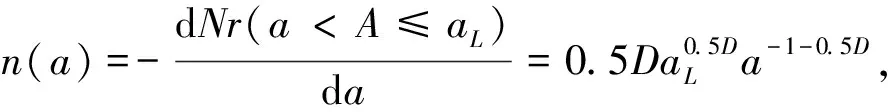
(6)
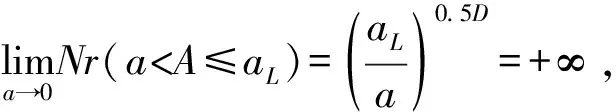
按照核心关系式(6)可得柔性结合面无量纲法向总载荷[1]为:
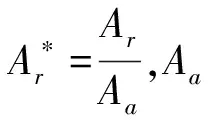
1.2 金属表面的静摩擦系数
在两接触体中存在组合法向和切向力,无文献记载应力场与实际接触面积的完全解。1983年Hamilton设想:两接触体承担法向弹性载荷Pe,由赫兹解得到的接触区域形状不受追加实用切向力Q的影响;假如比值Q/Pe<0.3,于是失效将首先发生在表面下,稍许远离当Q=0时赫兹解对应的失效点;一经当比值Q/Pe>0.3以后,失效点跃迁到表面,失效发生在接触边界的边远边缘上[4]。
现假如Q/Pe>0.3,接触边界边远边缘的表面应力场分别为:
(8)
σ2=0
(9)
(10)
式中:ν为较软材料的泊松比。
需要一提的是式(8)不同于文献[7]的式(2),式(10)不同于文献[11]的式(1)。
按照式(8)、(10)可得柔性结合面无量纲最大静摩擦力[1]为:
(11)
需要一提的是式(11)不同于文献[11]的式(22)、(23)。
根据式(7)暨式(11)可得柔性结合面的静摩擦系数为:
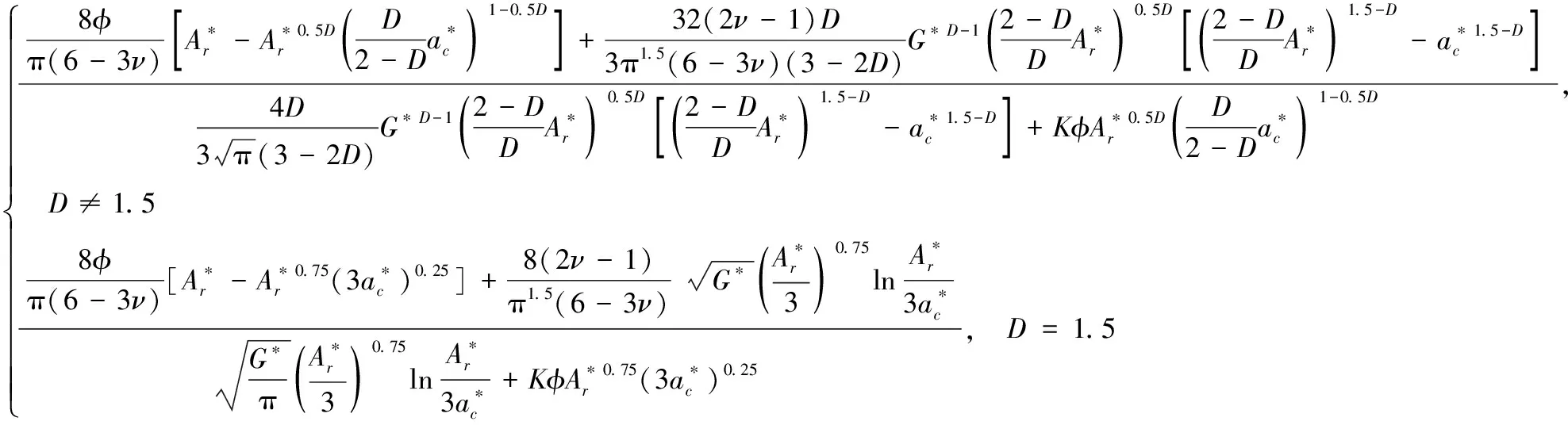
(12)
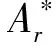
2 辨识两个分形参数的结构函数方法
功率信号式(1)的自相关函数[20]为:
(13)
将式(1)代入式(13)得:
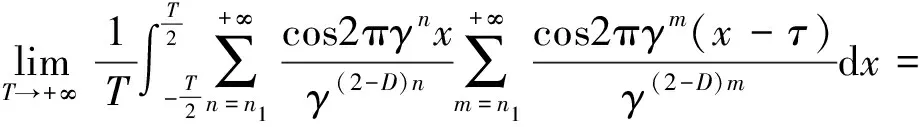
(14)
需要指出的是,从式(14)的倒数第二式可知:若m≠n时,各项都是零,则只剩下m=n时的一项。
象函数2πδ(ω-ω0)的傅里叶逆变换[20]为:
(15)
式中:ω为无阻尼自然角频率。
则象原函数eiω0t的傅里叶变换为:
(16)
式中:δ(ω)为Dirac delta脉冲偶函数,单位是ω的倒数,且:
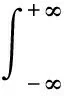
(17)
式中:c为非零实常数;y=|c|x为积分新变量。
因而有:
(18)
利用Euler公式,式(14)中通项象原函数cos2πγnτ的傅里叶变换[20]为:
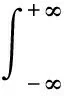
(19)
式中:f为无阻尼自然频率,不同于无阻尼自然角频率ω,ω=2πf。
将式(16)代入式(19)得:
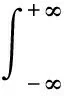
(20)
将式(18)代入式(20)得:
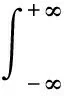
(21)
振幅频谱式(21)的图形见图1。考虑粗糙表面微观几何形貌的随机分布特点,如仅计及无阻尼自然频率f>0单边振幅频谱,将-γn相应的振幅0.5叠加在γn相应的振幅0.5上,合成可得总振幅为1。故可将式(21)近似改写成实际粗糙表面形貌的振幅频谱:
(22)
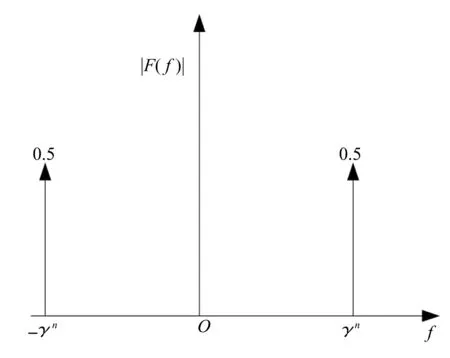
图1 式(14)中通项的振幅频谱
根据维纳-辛钦关系式[20]可得离散自相关函数式(14)的离散功率谱密度函数为:
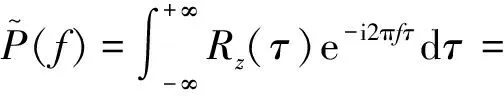
(23)
将式(22)代入式(23)得:
(24)
将离散功率谱密度函数式(24)转化为连续功率谱密度函数[21]:
(25)
式中:Δf为无阻尼自然频率的增量;Δn为无阻尼自然频率指数的增量;n(f)为无阻尼自然频率零点指数,且:
n(f)=logγf
(26)
将式(26)代入式(25)得:
(27)
需要注意,式(27)和文献[15]的式(6)、文献[22]的式(2)、文献[23]的式(2a)、文献[24]的式(10)均相异。
按照定积分的换元法得:
(28)
式中:x>0;β>0;z=xt为定积分新变量;Γ(β)为gamma函数。
由式(28)得:
(29)
随便查高等数学不定积分表得:
(30)
利用变量代换,下述定积分为:
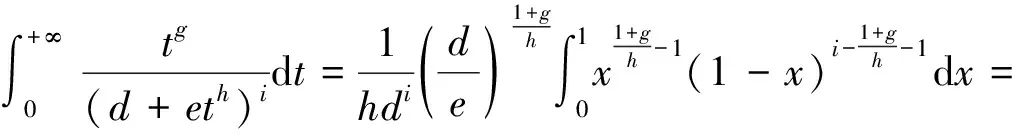
(31)
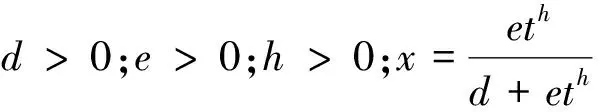
令d=e=i=1,h=2,由式(31)得:
(32)
用β-2代换式(32)中的g且使用余元公式得:

(33)
使用式(29)可将下列单重定积分化为二重定积分:
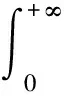
(34)
式中:β=5-2D∈(1,3)。
由式(28)可得t>0,将式(30)代入式(34)得:
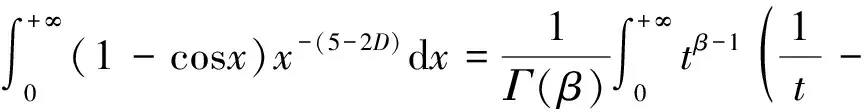
(35)
将式(33)代入式(35)得:
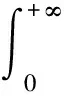
(36)
将式(34)中的注释β=5-2D代入式(36)得:
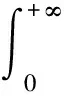
(37)
重点说明,式(37)亦皆相异于文献[23]的式(14)、文献[26]第215页的式(2)。
由Γ函数的递推公式及余元公式,式(37)可变形为:
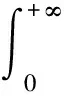
(38)
式(1)派生出函数z(x1)及z(x2)之间的结构函数为:
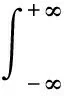
(39)
式中:〈 〉为无阻尼自然频率平均符号。
特别强调的是,式(39)亦全不同于文献[15]的式(8)、文献[27]的式(11)、文献[28]的式(2.3)。
根据式(27)可得双边连续功率谱密度函数为:
(40)
奇函数sin(x1-x2)f在对称区间(-∞,+∞)上对f的定积分是零,根据Euler公式,将式(40)代入式(39)得:
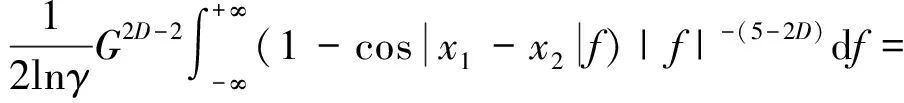
(41)
式中:x=|x1-x2|f为定积分新变量。
将式(38)代入式(41)得:
〈[z(x1)-z(x2)]2〉=
(42)
令x1=x,x2=x-τ(τ为尺度滞后),可得整体柔性结合面的结构函数为:
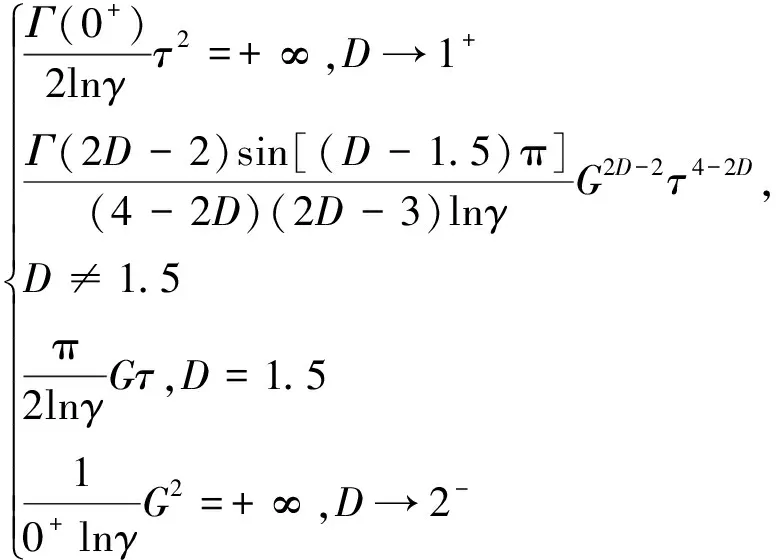
(43)
当量表面高度式(1)和两个粗糙表面1、2高度之间的关系为:
z(x)=z1(x)-z2(x)
(44)
式中:zj(x)为粗糙表面j的高度,j=1,2。
参考式(39)中“〈 〉”符号的运算规则,将式(44)代入式(43)得:
S(τ)=〈[z1(x)-z2(x)-z1(x-τ)+z2(x-τ)]2〉=〈[z1(x)-z1(x-τ)]2〉-2〈[z1(x)-z1(x-τ)][z2(x)-z2(x-τ)]〉+〈[z2(x)-z2(x-τ)]2〉
(45)
由于两粗糙表面在传统统计学上互不相关,则下列交叉乘积项为零:
〈[z1(x)-z1(x-τ)]×[z2(x)-z2(x-τ)]〉=0
(46)
仿照式(43),因此式(45)可变形为:
S(τ)=S1(τ)+S2(τ)
(47)
式中:Sj(τ)为粗糙表面j的结构函数,j=1,2。
令γ=γ1=γ2,不失去普遍性,将式(47)展开得:
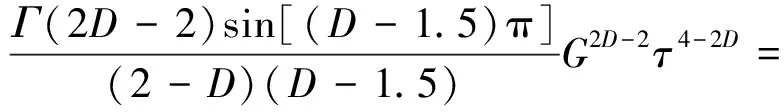
(48)
式中:γ为整体柔性结合面非整数相位随机参数;γj为表面j的相位随机参数,j=1,2;D为整体柔性结合面的分形维数;Dj为表面j的分形维数,j=1,2;G为整体柔性结合面的分形粗糙度;Gj为表面j的分形粗糙度,j=1,2。
文中大量涉及gamma函数,文献[29]仅提供gamma函数在闭区间1≤x≤2的以下近似解:
Γ(x)≈1-0.574 864 6(x-1)+0.951 236 3(x-1)2-0.699 858 8(x-1)3+0.424 554 9(x-1)4-0.101 067 8(x-1)5,1≤x≤2
(49)
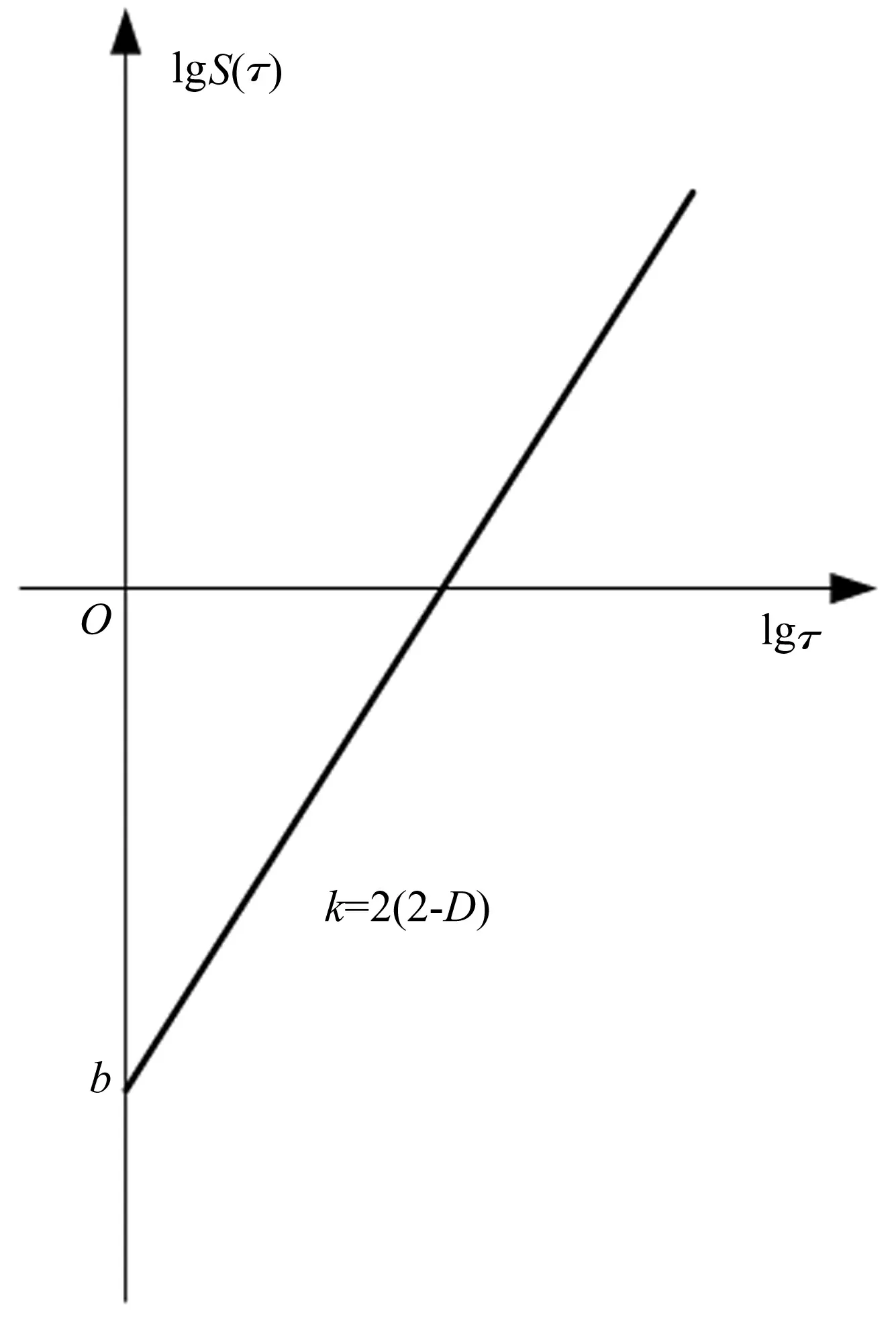
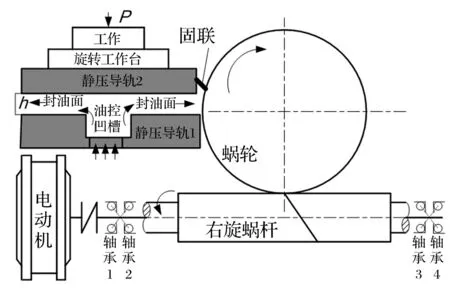
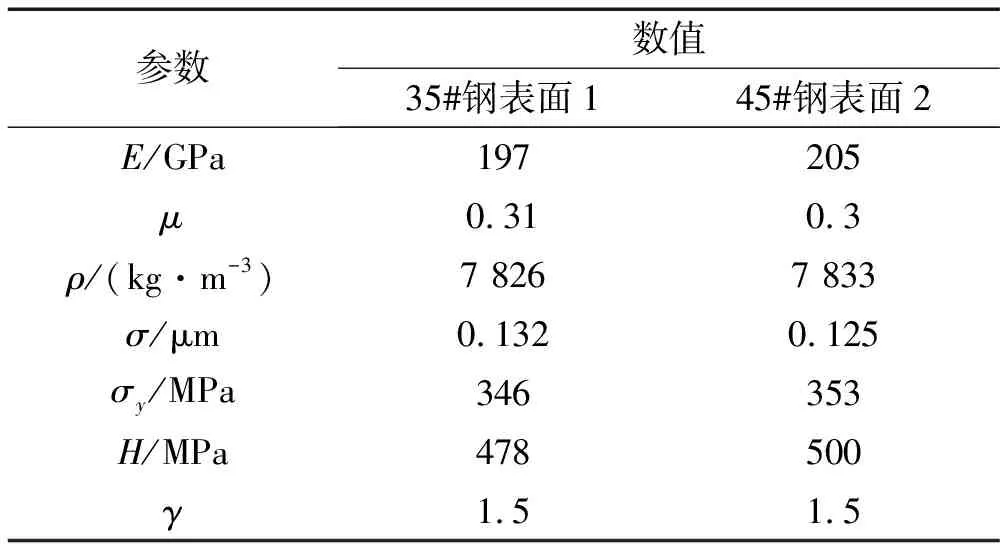
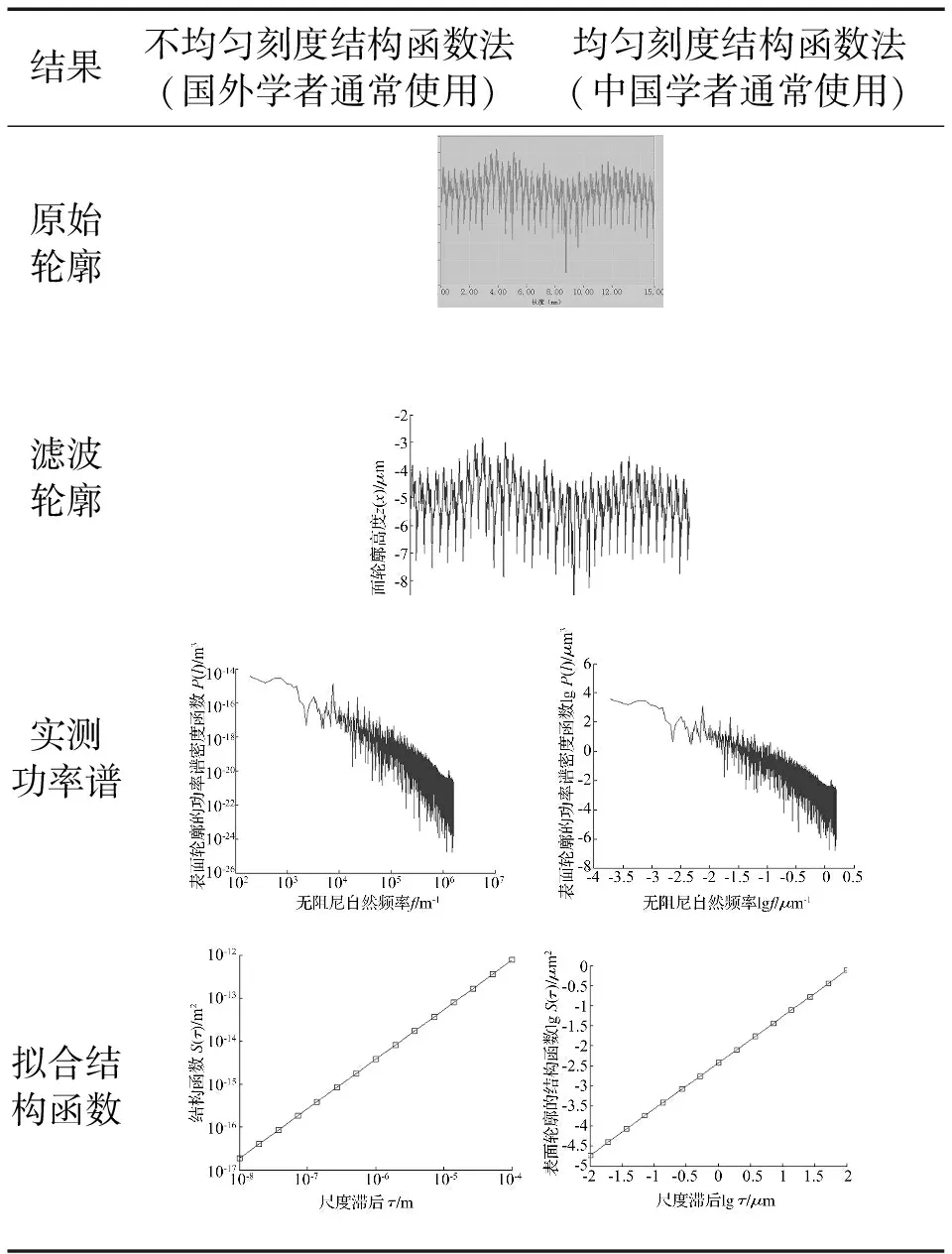
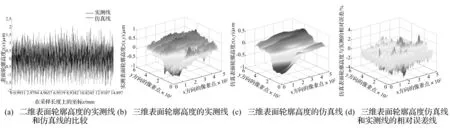
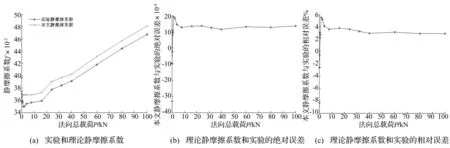
但式(49)不能解决0 x=0.01:0.1:2 004;% 2 004可取适当较大值 plot(x,gamma(x)) 文献[29]近似解与文中解的比较见图2,可见采用文中解可获取gamma函数。 图2 文献[29]解和文中解的比较 若G1=3.6×10-10m、G2=2.4×10-10m、γ=γ1=γ2=1.5时,粗糙表面1、2与整体柔性结合面的结构函数见图3。 图3 三种结构函数 此刻式(48)可简化为: (50) 为使关于自变量尺度滞后τ的恒等式(50)成立,可得要辨识整体柔性结合面的分形维数、分形粗糙度为: D=D1=D2 (51) (52) 图3(a)结果说明,在双对数坐标系下,整体柔性结合面的结构函数S(τ)和τ是线性关系,且和S1(τ)、S2(τ)均平行,整体柔性结合面在S(τ)轴上的纵截距都分别大于粗糙表面1在S1(τ)轴上的纵截距、粗糙表面2在S2(τ)轴上的纵截距,整体柔性结合面具有单重分形特性,整体柔性结合面的分形维数D和两粗糙表面的分形维数D1、D2相等(式(51)),整体柔性结合面的分形粗糙度G更大,即整体柔性结合面比互相接触两个粗糙表面更粗糙(式(52))。 图3(b)显示,在双对数坐标系下,整体柔性结合面的结构函数S(τ)和τ不再为线性关系,而表现为1条向上凹的曲线弧,且两粗糙表面的分形维数D1与D2偏离越悬殊,此曲线弧的弯曲程度越明显,曲线弧的第一段主要表示粗糙表面2的S2(τ)的分形性质,第二段主要表示粗糙表面1的S1(τ)的分形性质,说明整体柔性结合面具有双重分形性质,继而增加了求解非线性方程式(48)的难度。 严格站在高等数学的立场上,无条件能使关于自变量τ的方程式(48)恒成立。为求解此方程,首先按照两粗糙表面1、2的结构函数与式(47),得到整体柔性结合面的结构函数,该结构函数在双对数坐标系下虽不是1条直线,但利用最小二乘法可近似回归其为1条直线,然后可辩识整体柔性结合面的分形维数D、分形粗糙度G。 不失去普适性,根据式(43)可得一条直线方程: (53) 假定: k=2(2-D) (54) g=-lgG (55) 将式(54)、(55)代入式(53)得: (56) 再假定: (57) 将式(57)代入式(56)得: lgS(τ)=klgτ+b (58) 直线方程式(58)见图4。 图4 整体柔性结合面的常用对数结构函数 由式(54),D=2-0.5k依赖k。由式(57),g依赖b、D,因D依赖k,故g依赖b、k。由式(55),G=10-g依赖g,故G依赖b、k。 电动机在时间t秒钟内提供的额定功为: (59) 式中:TN为电动机额定转矩,N·m;n1为电动机实际转速,r/min。 电动机在时间t秒钟内提供的平均额定功率为: (60) 执行装置旋转工作台消耗的功率为: (61) 式中:T2为旋转工作台转矩,N·m;n2为旋转工作台转速,r/min;F为两静压导轨表面间最大静摩擦力[1],N;r为最大静摩擦力作用的当量半径,mm;f为两静压导轨表面间的静摩擦系数;P为加载重物的重量,即法向总载荷[1],N。 电动机的额定功率是相应于额定环境温度40 ℃时的允许输出功率,故当环境温度高于或低于40 ℃时,电动机允许输出的功率可适当减小或增加。根据式(60),增减后的允许输出功率为: (62) 式中:α为满载时的不变损耗(包括铁损耗、机械损耗与附加损耗)和可变损耗(铜损耗)的比值;θ为实际环境温度;θN为额定温升;ξ为电动机负载率。 在电动机低转速情况下,使旋转工作台刚刚开始运动,得到静摩擦系数。工作台旋转消耗的功率等于驱动电机的输出功率,根据传递过程中的机械损失,可以得到功率平衡关系: P2=ηP1 (63) 将式(61)、(62)代入式(63)得: (64) 式中:η为普通圆柱蜗杆传动的总效率,且: η=η1η2η3 (65) 式中:η1为啮合摩擦损耗效率;η2为轴承摩擦损耗效率;η3为溅油损耗效率,且: (66) 式中:γ为普通圆柱蜗杆分度圆柱上的导程角;φv为当量摩擦角。 按照式(64),如果获得电动机在线运行时的n1、ξ,则能得到不同法向总载荷P时的静摩擦系数。结合面接触模型是描述两粗糙表面相接触表面微凸体的接触特性,本文的理论部分[1]并没有分析液体与粗糙表面接触的接触特性。实验是液体静压导轨接触表面,两静压导轨通过油膜(通常油膜厚度为5、7、9、14 μm等)而相互分开,静压导轨的两金属表面在微观状态下是不直接接触的,是液体与金属粗糙表面接触(否则就不是静压导轨),若考虑液体、油膜等非直接接触特性而求解的摩擦系数是微观摩擦系数。为使实验与两金属粗糙表面相接触的理论较好地吻合,获得能应用于实际工程的整个结合面的宏观摩擦系数,一方面,在实验前,先将两个静压导轨1、静压导轨2从机床部件中相互分离,然后将两个静压导轨1、静压导轨2的结合表面在丙酮中通过超声波清洗50 min,最后在去离子水中冲洗后,用流动的氮气吹干,即让两个静压导轨成为两干接触表面,也即两个静压导轨在短时间内处于非正常工作状态,使用环境愈加恶劣;另一方面,在实验的过程中在满足工况的前提条件下,装配两个静压导轨1、静压导轨2时,尽可能使油膜厚度小,如取1 m,使静压导轨的两金属表面逼近接触。如上所述,实验方案见图5,h为公称油膜厚度。 图5 实验方案 在武汉重型机床集团有限公司YK31320型普通滚齿机上进行实验,见图6。实验时的面板数据见图7。 图6 YK31320型普通滚齿机 研磨方式加工两液体静压导轨接触表面。采用英国Micro Materials Ltd制造的NanoTest®600型纳米压痕仪测定粗糙表面薄膜的硬度H,为了减少基体对薄膜硬度测量的影响,选择压入深度为100nm,每个样品取5个点进行测量,取平均值。液体静压导轨的参数见表1。 表1 两液体静压导轨表面的参数 使用英国公司Charlotte Research Institute的Taylor-Hobson Form TalySurf 5-120型表面轮廓仪,放大倍率为×1 000,采样长度为15 mm,采样间距为1 m,采样段数为5,最小二乘滤波,离散化采样点数为15 000。测试环境温度为23.5 ℃,空气相对湿度为58%。 设采样长度T=15 mm;无阻尼自然频率间隔为Δf=1/T;采样表面轮廓高度的离散数据点数为l,取l=15 000;采样间隔为Δx,取Δx=1 μm;空间采样点数为Ns=T/Δx=15 000,将数据补齐为大于l且为2的整数幂次方的数,选择Ns=214>l;采样频率为fs=1/Δx;最高频率为fmax,取fmax=0.5fs;设定无阻尼自然频率变化范围为f=fmax(0∶0.5Ns-1)/Ns;对表面轮廓信号表达式(1)的z(x)进行补零的Fourier变换,把z(x)的尾部补零使z(x)的长度达到Ns,可得补零的Fourier变换Y=fft(z,Ns);按照Y获得功率谱密度函数P(f)=|Y|2/Ns,根据式(39)得到柔性结合面的结构函数S(τ),然后使用最小二乘法的一次多项式拟合实测数据(lgτ,lgS(τ)),可获取常用对数结构函数(图4)。 表2 整体柔性结合面研磨时的编程情况 图7 实验面板数据 整体柔性结合面研磨时的情形见表2,不均匀刻度结构函数方法应用的是国际单位,使用的符号是斜率k1、纵截距b1、分形粗糙度的指数g1、分形维数D1、分形粗糙度G1,国外研究人员习惯使用;均匀刻度结构函数方法以长度单位微米为出发点,应用的符号是斜率k2、纵截距b2、分形粗糙度的指数g2、分形维数D2、分形粗糙度G2,中国研究人员习惯使用。这二种方法辨识的五个参数分别为k1=0.993 4,b1=-8.165 2,D1=1.503 3,g1=8.697 5,G1=2.006 6×10-9m;k2=0.993 4,b2=-2.125 8,D2=1.503 3,g2=2.697 5,G2=2.006 6×10-9m。则整体柔性结合面的两个重要表征参数为D=1.503 3,G=2.006 6×10-9m。 将辨识的整体柔性结合面参数D、G代入式(1),可得二维表面轮廓高度的仿真线,二维表面轮廓高度的实测线、仿真线见图8(a)。二维表面轮廓高度的模拟函数式(1)可由下面三维表面轮廓高度的Ausloos-Berman函数简化而得: (67) 式中:x,y为粗糙表面轮廓的位移坐标;L为取样长度;M为曲面褶皱的重叠数;γ为大于1的常数,通常取γ=1.5;n为无阻尼自然频率序数;nmax为最高频率序数,nmax=int[ln(L/Ls)/lnγ],Ls为截止长度,通常近似为材料的原子间距离;φm,n为随机相位,取值范围为[0,2π]。 将辨识的整体柔性结合面参数D、G代入式(67),可得三维表面轮廓高度的仿真线,三维表面轮廓高度的实测线见图8(b)、仿真线见图8(c)、两者之间的相对误差见图8(d)。根据图8(d),仿真线和实测线之间的相对误差较小,说明辨识的整体柔性结合面参数实用有效。 图8 表面轮廓高度的实测线和仿真线的比较 图9 理论静摩擦系数和实验的比较 例如在加载重物的重量P=100 kN时,将表1中的数据与D=1.503 3,G=2.006 6×10-9m代入式(12)、(64),分别可得整体柔性结合面的理论静摩擦系数为f=0.480 51,实验静摩擦系数为f=0.466 93。 在加载不同质量的重物情况下,理论静摩擦系数和实验的比较见图9。观察图9(a),在狭窄的小载荷0~1.6 kN范围内,即电动机在低转速工况下,实验静摩擦系数随法向总载荷的增大而变小(由于使旋转工作台开始旋转,施加在旋转工作台上的切向总载荷愈来愈大),且实验静摩擦系数会呈现忽高忽低的突变波动情况(由于电动机的低转速迫使机床静压导轨的动态性能处于不稳定的爬行,强烈影响静压导轨的表面粗糙度,引起摩擦副的剧烈磨损);在宽广的中等载荷1.6~100 kN范围内,即电动机在近似稳定中等转速工况下,实验静摩擦系数随法向总载荷的增大而增大,且理论静摩擦系数比实验大(由于实际两静压导轨表面之间存在最小公称油膜厚度的流体膜,常使一个静压导轨处于似浮非浮状态)。根据图9(b),理论静摩擦系数和实验的绝对误差在-0.033 02~0.019 26之间。根据图9(c),理论静摩擦系数和实验的相对误差在-8.323%~5.512%之间。值得提醒:由于实际静摩擦系数的变化范围狭窄,所以给出绝对误差比提供相对误差更有说服力。 (1)给出关于粗糙表面微凸体接触点面积a的概率分布密度n(a)的推导过程。该概率分布密度适用于机械加工粗糙表面,不管磨削、铣削、车削表面都满足此概率分布密度的关系式。 (2)给出计算整体柔性结合面两个分形参数的结构函数方法。该结构函数方法可以从测量的实际数据入手,能求解特定整体柔性结合面分形维数、分形粗糙度的具体数字。本文严格区分无阻尼自然频率f和无阻尼自然角频率ω,ω=2πf,本文求解的是以f为自变量的功率谱密度函数和结构函数。文献[30]将f和ω都当作ω,不合理。对于以ω为自变量的功率谱密度函数和结构函数的修正计算是后续重点研究的内容。 (3)对文献[1]的理论计算和分析进行实验佐证。在一定加载重物的范围内,理论静摩擦系数和实验的绝对误差在-0.033 02~0.019 26之间,理论静摩擦系数和实验的相对误差在-8.323%~5.512%之间。 参 考 文 献 [1]田红亮,赵春华,方子帆,等. 金属材料表面静摩擦学特性的预测研究——理论模型[J]. 振动与冲击,2013,32(12):40-44,66. TIAN Hong-liang, ZHAO Chun-hua, FANG Zi-fan, et al. Predication investigation on static tribological performance of metallic material surfaces- theoretical model [J]. Journal of Vibration and Shock,2013,32(12):40-44,66. [2]赵 飞,逄显娟,杜三明,等. MoSx掺杂DLC薄膜的摩擦磨损行为Ⅰ:载荷的影响[J]. 摩擦学学报,2012,32(5):516-523. ZHAO Fei, PANG Xian-juan, DU San-ming, et al. Friction and wear behaviors of MoSx-doped DLC films Ⅰ:effect of normal load [J]. Tribology,2012,32(5):516-523. [3]赵 飞,逄显娟,杜三明,等. MoSx掺杂DLC薄膜的摩擦磨损行为Ⅱ:速度的影响[J]. 摩擦学学报,2012,32(5):524-530. ZHAO Fei, PANG Xian-juan, DU San-ming, et al. Friction and wear behaviors of MoSx-doped DLC films Ⅱ:effect of sliding speed [J]. Tribology,2012,32(5):524-530. [4]Chang W R, Etsion I, Bogy D B. Static friction coefficient model for metallic rough surfaces [J]. Transactions of the ASME Journal of Tribology,1988,110(1):57-63. [5]Greenwood J A, Williamson J B P. Contact of nominally flat surfaces [J]. Proceedings of the Royal Society of London:Series A Mathematical and Physical Sciences,1966,295(1442):300-319. [6]You J M, Chen T N. A static friction model for the contact of fractal surfaces [J]. Proceedings of the Institution of Mechanical Engineers, Part J:Journal of Engineering Tribology,2010,224(5):513-518. [7]尤晋闽,陈天宁. 结合面静摩擦系数的统计模型[J]. 振动与冲击,2010,29(12):26-29. YOU Jin-min, CHEN Tian-ning. Statistical model of static friction coefficient between joint surfaces [J]. Journal of Vibration and Shock,2010,29(12):26-29. [8]吕振林,刘晶歌,肖琪聃,等. Ti3AlC2陶瓷的制备及其摩擦磨损性能[J]. 硅酸盐学报,2012,40(4):503-506. LÜ Zhen-lin, LIU Jing-ge, XIAO Qi-dan, et al. Fabrication of Ti3AlC2by reactive sintering and its friction and wear behavior [J]. Journal of the Chinese Ceramic Society,2012,40(4):503-506. [9]盛选禹,雒建斌,温诗铸. 基于分形接触的静摩擦系数预测[J]. 中国机械工程,1998,9(7):16-18. SHENG Xuan-yu, LUO Jian-bin, WEN Shi-zhu. Static friction coefficient model based on fractal contact [J]. China Mechanical Engineering,1998,9(7):16-18. [10]Majumdar A,Bhushan B. Fractal model of elastic-plastic contact between rough surfaces [J]. Transactions of the ASME Journal of Tribology,1991,113(1):1-11. [11]Sui C F, Sheng X Y. Fractal transition model in predicting static friction coefficient [J]. Multidiscipline Modeling in Materials and Structures,2009,5(4):345-348. [12]田红亮,赵春华,朱大林,等. 弹塑性三维各向异性分形表面的接触分析[J]. 三峡大学学报(自然科学版),2012,34(1):69-73. TIAN Hong-liang, ZHAO Chun-hua, ZHU Da-lin, et al. Contact analysis of elastoplastic three-dimensional anisotropic fractal surfaces [J]. Journal of China Three Gorges University (Natural Sciences),2012,34(1):69-73. [13]田红亮,朱大林,秦红玲. 固定接触界面法向静弹性刚度的改进弹簧分形模型[J]. 三峡大学学报(自然科学版),2012,34(6):83-88. TIAN Hong-liang, ZHU Da-lin, QIN Hong-ling. Improved spring fractal model for normal static elastic stiffness of stationary contact interface [J]. Journal of China Three Gorges University (Natural Sciences),2012,34(6):83-88. [14]魏 龙,刘其和,张鹏高. 基于分形理论的滑动摩擦表面接触力学模型[J]. 机械工程学报,2012,48(17):106-113. WEI Long, LIU Qi-he, ZHANG Peng-gao. Sliding friction surface contact mechanics model based on fractal theory [J]. Journal of Mechanical Engineering, 2012,48(17):106-113. [15]贺 林,朱 均. 粗糙表面接触分形模型的提出与发展[J]. 摩擦学学报,1996,16(4):375-384. HE Lin, ZHU Jun. Fractal model for contact of rough surfaces [J]. Tribology,1996,16(4):375-384. [18]田红亮,刘芙蓉,朱大林. 4种NET欧拉-伯努利直梁的动力学特性[J]. 三峡大学学报(自然科学版),2013,35(4):85-93. TIAN Hong-liang,LIU Fu-rong, ZHU Da-lin. Dynamic properties of four NET Euler-Bernoulli straight beam [J]. Journal of China Three Gorges University (Natural Sciences),2013,35(4):85-93. [19]李彦青,殷德顺,吴 浩. 变分数阶微积分在描述材料力学性质演变方面的应用[J]. 三峡大学学报(自然科学版),2012,34(6):63-67,76. LI Yan-qing, YIN De-shun, WU Hao. Application of variable-order fractional calculus to description of evolution of mechanical properties of materials [J]. Journal of China Three Gorges University (Natural Sciences),2012,34(6):63-67,76. [20]卢文祥,杜润生. 机械工程测试·信息·信号分析[M]. 2版. 武昌:华中科技大学出版社,2004. [21]Berry M V, Lewis Z V. On the Weierstrass-Mandelbrot fractal function [J]. Proceedings of the Royal Society of London:Series A Mathematical and Physical Sciences, 1980,370(1743):459-484. [22]Bhushan B, Majumdar A. Elastic-plastic contact model for bifractal surfaces [J]. Wear,1992,153(1):53-64. [23]Ganti S, Bhushan B. Generalized fractal analysis and its applications to engineering surfaces [J]. Wear,1995,180(1-2):17-34. [24]Majumdar A, Tien C L. Fractal network model for contact conductance [J]. Transactions of the ASME Journal of Heat Transfer,1991,113(3):516-525. [25]《数学手册》编写组. 数学手册[M]. 北京:高等教育出版社,2008:590. [26]Wang S, Komvopoulos K. A fractal theory of the temperature distribution at elastic contacts of fast sliding surfaces [J]. Transactions of the ASME Journal of Tribology,1995,117(2):203-215. [27]Majumdar A, Bhushan B. Role of fractal geometry in roughness characterization and contact mechanics of surfaces [J]. Transactions of the ASME Journal of Tribology,1990,112(2):205-216. [28]Berry M V. Diffractals [J]. Journal of Physics A:Mathematical and General,1979,12(6):781-797. [29]郭建英,孙永全,王铭义,等. 基于计算机仿真的风电机组系统可靠性综合[J]. 机械工程学报,2012,48(2):2-8. GUO Jian-ying, SUN Yong-quan, WANG Ming-yi, et al. System reliability synthesis of wind turbine based on computer simulation [J]. Journal of Mechanical Engineering,2012,48(2):2-8. [30]田红亮,刘芙蓉,方子帆,等. 结合部静摩擦因数修正与定量实验验证[J]. 农业机械学报,2013,44(10):282-293. TIAN Hong-liang,LIU Fu-rong, FANG Zi-fan, et al. Correction of static friction coefficient for joint interface and quantitative test confirmation [J]. Transactions of the Chinese Society for Agricultural Machinery,2013,44(10):282-293.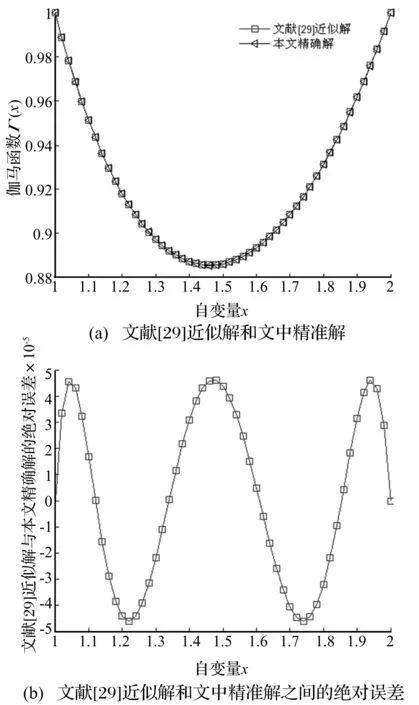
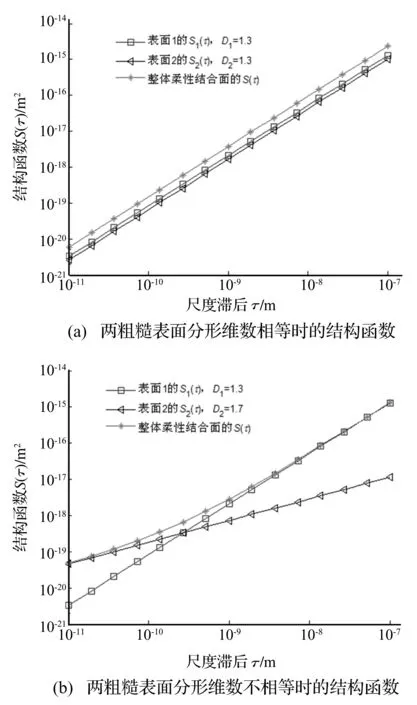
2.1 两粗糙表面分形维数相等
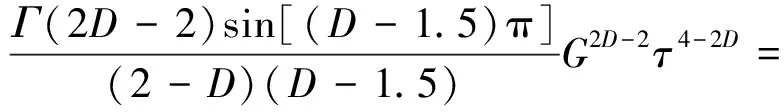
2.2 两粗糙表面分形维数不相等
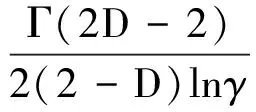
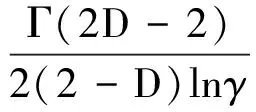
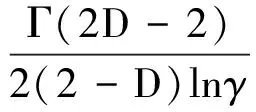
3 静摩擦系数理论解的实验佐证
3.1 实验方案
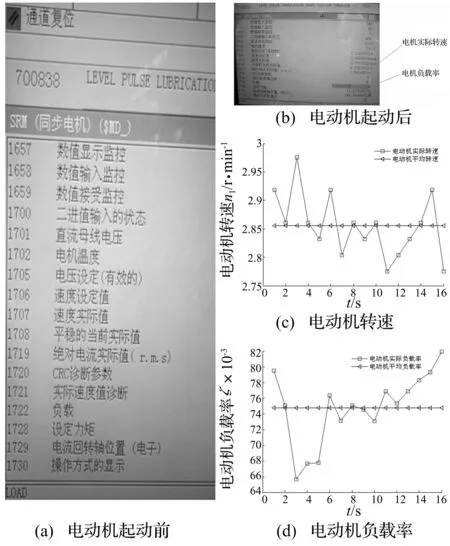
3.2 实验过程

3.3 分形参数实验辨识与静摩擦系数的求解
3.4 理论静摩擦系数和实验的误差
4 结 论

