基于Jacobi-Davidson算法的大规模模态分析并行计算研究

范宣华, 陈 璞, 吴瑞安, 肖世富

(1.中国工程物理研究院 总体工程研究所，四川 绵阳 621900； 2.北京大学 力学与工程科学系，北京 100871)

模态分析是工程结构动力学数值模拟过程中极其重要的环节之一，工程结构的日趋复杂以及精度可靠性要求的不断提高对数值模拟提出了新的挑战，往往要求结构有限元规模达到数百万甚至千万自由度以上。传统的商业分析软件如ANSYS、Nastran等在计算规模和效率等方面受到了很大限制，自主研究基于先进算法的并行模态分析程序显得尤为重要。

模态分析在数学上可以归结为大型稀疏矩阵特征值问题。对于该类问题的研究大多基于子空间投影技术，即借助一系列低维数的子空间，将一个大型稀疏矩阵A向这些子空间进行投影，将大型矩阵A的部分特征值问题转化为中小规模矩阵的特征值问题，利用中小规模矩阵的一些成熟算法求解其特征对，并形成对A矩阵部分特征对的一个近似[1-3]。根据子空间构造方式不同主要有两条思路，一是Krylov子空间类算法；二是Davidson类算法。

Krylov子空间类算法在大型稀疏矩阵特征值问题的研究过程中占据了重要地位，其中以Lanczos方法[4]最为著名。后来Lanczos方法发展成很多的变种形式，其中Sorensen等[5]提出的隐式重启动Arnoldi/Lanczos方法和Wu等[6]提出的thick-restart Lanczos方法最为著名，至今影响深远。然而对于模态分析，为求解最小特征值部分，需进行谱变换处理，由此导致每步子空间迭代过程中都要求解一个大型线性病态方程组，迭代求解难以收敛，大多采用直接法进行矩阵分解[1-3]。然而分解过程导致了内存的大量消耗，并在一定程度上破坏了原稀疏矩阵的结构特性，而且分解还带来了各并行进程间的通讯量剧增，不利于并行计算的扩展。

Davidson类算法属于非Krylov类子空间投影算法，它们和Krylov子空间投影算法都采用了瑞利-里兹过程，但是构造正交基的方式不同。实际上，Davidson类算法可以看成是Krylov子空间类算法的预处理版本[7]，即相当于在Krylov类算法每步子空间扩展时添加了一个预处理矩阵。该类算法中最值得关注的一种算法是J-D方法[8]，该方法通过在某一近似特征向量的正交补空间上求解“修正方程”扩展子空间向量，对修正方程的求解大多采用迭代法，即J-D算法通过内-外层迭代求解特征对，外层迭代扩展子空间，内存迭代求解修正方程。这样以来算法主要涉及矩阵-向量乘、向量积等运算，不但特征矩阵的稀疏结构得以保留，各并行进程间通讯量较Krylov子空间类算法也大大降低，非常有利于并行计算可扩展性能的提升。

本文的研究就是基于J-D算法，通过添加谱变换、预处理以及收缩和重启动技术将其改造成适合大规模模态分析的算法；并基于PANDA框架[9]和特征值求解包SLEPc[10]，对一简化飞行器有限元模型进行了大规模模态分析并行计算研究。

1 模态分析中的J-D算法设计

模态分析的数学本质就是求解如下广义矩阵特征值问题：

Kx=λMx

(1)

式中：K为刚度矩阵，M为质量矩阵。K和M可以通过对工程结构进行有限元离散和积分得到，二者都是大型稀疏、对称(半)正定矩阵。模态分析就是求解式(1)的多个低阶特征对。

标准的J-D算法[8]是通过迭代求解一个“修正方程”来扩张子空间，通过设定一个目标值τ来控制特征值收敛范围。对于大规模模态分析，需要围绕“修正方程”求解、收缩和重启动、谱变换等几个方面对算法进行优化或改进。

首先，对于广义Hermitian特征值问题，修正方程表达式变为[1]：

(2)

式中，*表示共轭转置，θk和uk分别是里兹值和里兹向量，t是需要求解的正交补向量，rk是迭代产生的留数向量rk=Kuk-θkMuk。采用M-正交技术，可以将式(1)缩减成Schur形式[1-3]：

KQk=ZkDk

(3)

式中，矩阵Dk是k×k阶对角阵，对角线元素为广义特征问题(1)的k个特征值；Qk是关于M正交的n×k阶矩阵，存放着k个相应的特征向量，Zk=MQk。通过式(3)可以将修正方程(2)转换成如下形式：

(4)

对于该修正方程的求解，需要采取预处理技术，假定P是K-θkM的一个预条件子，即满足P-1(K-θkM)≈I，则式(4)的预条件子可以取为：

(5)

施加预条件后，修正方程(4)变为：

(6)

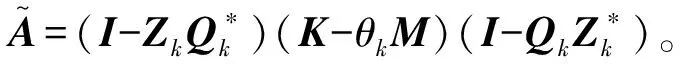
在采用J-D算法进行求解时，随着外层迭代子空间维数的增长，存储和计算量将会显著增加，不利于大规模模态分析。为此，需要限制外部子空间的最大维数，当子空间达到最大维数mmax时，重新迭代扩张子空间，即重启动。在重启动时，为充分利用上次子空间扩张的信息，通常取最靠近目标值τ的mmin个里兹值对应的里兹向量作为重启动初始迭代子空间。另一方面，随着迭代进行，部分特征对会趋向收敛，需要将相应的里兹向量从迭代子空间中“剔除”，以便于算法继续搜索下一个特征对。这时采用的是一种收缩策略，即将新的扩张子空间向量与已经收敛的特征向量做正交化处理。

图1 模态分析问题的J-D算法

综合以上分析，给出模态分析的J-D算法如图1所示。理论上，J-D算法当目标值设置τ高于最大特征值时，算法会收敛于最大特征值部分；当目标值τ低于最小特征值时，算法将收敛于最小特征值部分。而实际上，由于J-D算法的根基还是幂法和瑞利-里兹过程，里兹值总是趋向于最大特征值部分，虽然通过小的目标值设定和“修正方程”的反复修正会将最大特征值求解逐步转到最小特征部分，但收敛速度会非常慢甚至不收敛。为此，我们考虑在J-D算法中添加一个常用的Shift-Invert谱变换[12]:

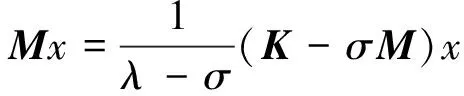
(7)

式中，σ为移位值，取值一般略低于最低阶特征值。这样以来，分别以矩阵M和K-σM代替原问题的K和M，以θ=1/(λ-σ)代替λ，将会得到θ的最大特征值部分，再反算得到最小的λ。若对应工程问题没有刚体模态，可以取σ=0。这样只需在J-D算法中将K和M调换即可，这时设置目标值τ略大于最低阶特征值的倒数，将会得到很好的收敛效果。

2 并行计算实现

最近10多年来，大批学者和工程师们基于各种大型稀疏矩阵特征值问题的算法，开发了很多的特征值并行求解软件包，这些软件包基本都是开源的，可以在因特网上进行下载。文献[13]对这些数值软件包进行了较为全面的概括。在这些软件包中， SLEPc软件包[10]得到了广泛的关注，SLEPc基于MPI并行通讯标准，已经集成了很多软件库和算法，并且具备与其他一些软件库的接口功能，用户可以在其基础上添加特征值解法器。2011年，SLEPc软件包的3.1版本已经对Davidson类算法进行了代码实现。

虽然目前关于大规模稀疏矩阵特征值并行计算问题的算法理论和代码开发非常多，但应用于具体工程问题的研究却非常少。究其原因，一个数值算法应用于实际工程，还需要很多其他学科知识和辅助技术手段，以大规模模态分析并行计算为例，需要力学、计算机、数学等多学科知识和丰富的工程数值计算能力。目前找到模态分析并行实践的见文献[14]，该文献采用AMG预处理技术，分别采用Lanzos方法、Davidson方法以及LOBPCG等方法实现了航母189万自由度有限元模型的模态分析并行计算，被认为是当时最具挑战性的工作。

对于模态分析并行计算的实现采用流程如下：

(1)通过商业有限元软件如MSC.Patran进行前处理建模，并根据不同单元类型、不同材料和边界约束等对有限元模型进行分组处理。然后将这些单元节点信息以MSC.Patran 的中性文件(neutral)形式进行输出。目前采用MSC.Patran可以在普通工作站上建立千万自由度以上的有限元模型。

(2)利用并行计算框架PANDA[9]生成质量矩阵M和刚度矩阵K。PANDA框架是由中国工程物理研究院开发的一个有限元并行框架，包含了与前处理商业软件的接口以及一些解法器接口。通过PANDA的接口功能，MSC.Patran中的有限元网格信息被转换成PANDA可以识别的网格信息，再结合PANDA集成的Metis[15]图剖分软件对有限元网格进行区域分解，利用不同子区域并行生成质量和刚度矩阵。

(3)通过PANDA框架调用特征值算法进行求解。将SLEPc及相关辅助软件包集成到PANDA框架中，并根据以上算法改进对SLEPc软件包的具体实现进行相应改进和添加，由PANDA框架调用改进后的J-D算法并行求解特征对。求解过程中各进程的并行通信由PANDA框架和SLEPc软件包通过MPI进行管理。

3 模态分析算例

通过一个具体工程算例对Jacobi-Davidson算法进行一个详细测评。采用的工程模型为一简化飞行器有限元模型，如图2所示。模型底部固定，采用八节点六面体单元，在MSC.Patran中分别建立了数十万至上千万自由度规模的测试算例，所有算例均求解前20阶模态频率。并行计算测试在某曙光5000A机群上进行，该机群由16个刀片节点构成，每个节点由双路四核Intel Xeon E5550 2.66 GHz处理器共享16 GB内存，各节点间通过千兆网连接。

3.1 J-D算法参数设置与结果对比

从图1中的Jacobi-Davidson算法可以看出，决定算法收敛速度的因素很多。为更合理选取各参数，首先对飞行器71万(n=710 526)自由度规模进行了一系列测试。

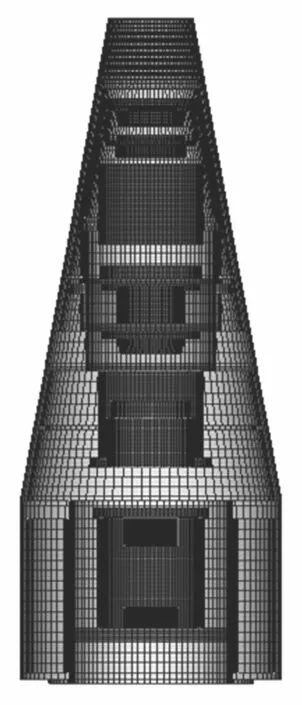
图2 飞行器有限元模型

对于目标值τ的选取，通过式(7)的谱变换，已经将最小特征值问题转换成了算法更容易收敛的最大特征值问题。故τ的选取只需要略大于最小特征值的倒数即可，对于本算例，最小特征值的倒数在10-7量级，故取τ=1e-6。需要注意的是，τ的取值不能小于最小特征值的倒数，否则会出现基频附近漏根的情形。对于外层迭代子空间的最大维数mmax，由于施加了重启动策略，一般选取求解特征值个数的两倍左右即可，本算例取mmax=41。更大的子空间维数会带来内存需求的快速增加。

修正方程的求解属于内层迭代，采用了Jacobi预处理和CG迭代解法。内层迭代如需要足够精确，则需要足够多的迭代步数，会严重影响算法的效率。故一般只采用一个近似迭代过程，主要控制迭代的步数，算法本身的精度通过外层迭代相对误差控制，一般取1e-4就足够了。内层迭代和外层迭代之间存在一个平衡关系，一般说来，内层迭代的增加会带来外层迭代的减少，但内层迭代占用的更多时间也会使得整个计算时间增多。表1给出了71万模型在16进程下内层迭代步数所致外层迭代步数及算法总时间的关系(重启动向量个数固定为8个)。从表中可以看出，内层迭代取30步左右达到最佳。需要说明的是，表1和后面表格中所指的计算时间均是调用J-D算法的运行时间，不包含并行区域分解和形成总体刚度、质量矩阵的时间(事实上，并行区域分解和形成总体刚度、质量矩阵的时间较J-D算法运行时间要少得多，基本可以忽略)。

当子空间维数达到最大维数时进行重启动，重启动向量的个数也会对收敛速度造成影响。重启动向量一般选取最接近目标值的几个里兹值对应的里兹向量作为初始向量空间，这些初始向量包含了大量上次子空间扩张的信息，其个数的选取也需要权衡，选的过少，则不能充分利用上次子空间扩张的信息，选的过多，则除继承了上次子空间扩张的有用信息外，会掺杂进来很多不需要的信息。表2给出了71万模型在16进程下重启动向量个数选取所致外层迭代步数及算法总计算时间的关系(内层迭代固定为30步)。在重启动向量取12个左右达到最佳。

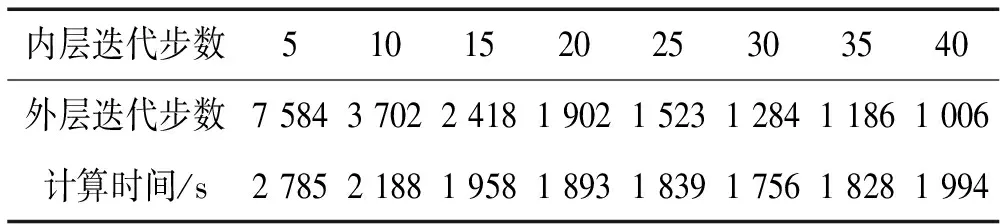
表1 内层迭代与外层迭代及计算时间的关系

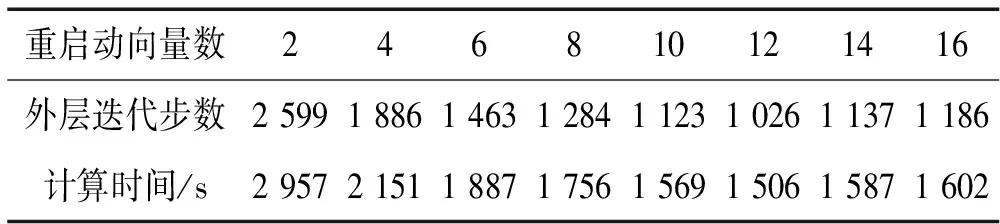
表2 重启动向量个数与外层迭代及计算时间的关系

通过以上测试和比较，可以基本确定J-D算法求解前20阶模态频率时的各控制参数，目标值τ取1e-6，子空间最大维数取41，内层迭代步数取30，重启动向量维数取12，外层迭代控制误差1e-4。

除J-D算法本身参数优化设置外，还就算法求解的正确性与Krylov子空间类算法中的隐式重启动Lanczos方法(IRLM)求解结果进行了对比，IRLM采用了Cholesky分解直接求解谱变换后的线性方程组，数值精度接近计算机浮点运算精度，通常被认为是“精确解”[1-2]。表3对比了两种方法前10阶的模态频率结果。从中可以看出，二者计算结果几乎完全一致，最大相对误差在0.3%以内。

表3 J-D算法与IRLM算法计算结果比较

3.2 大规模并行测试

在上节参数选取和算法正确性得以验证的前提下，通过该飞行器简化模型对J-D算法进行了并行可扩展性测试，主要包括计算规模和并行加速比。

计算规模方面，在128个进程下分别测试了飞行器有限元模型数十万到上千万自由度规模并行计算情况。图3给出了1 025万自由度规模前20阶模态频率计算过程中的迭代收敛历史，从中可以看出迭代误差随外层迭代的变化情况，当迭代误差低于1e-4，便得到一个特征对，算法继续迭代并寻找下一个特征对。在继续寻找下一个特征对的过程中，由于要不断更新求解“修正方程”寻找新的特征方向，计算误差在迭代过程中有所震荡，但经过多次修正后会在有限的迭代步内逐渐减小直至收敛(误差低于1e-4)。表4给出了不同规模下内存需求、外层迭代步数、计算时间及一阶固有频率的变化情况。从中可以看出，J-D算法的内存占用很小，并且随计算规模增大呈现线性增长趋势，这与Krylov子空间类算法相比是一个很大的优势，Krylov子空间类算法由于采用了直接法求解谱变换后的线性方程组，导致内存占用非常大(经测试IRLM方法在112万自由度规模所占用的内存便高达32 GB)，而且随规模增大，所需内存的增长也远超线性。随计算规模增大，外层迭代步数有所增加；1 025万自由度规模和71万自由度规模对应的一阶固有频率变化在8%以上，随着规模增大，一阶频率逐渐趋于稳定，从这点也可以看出大规模并行计算的必要性。

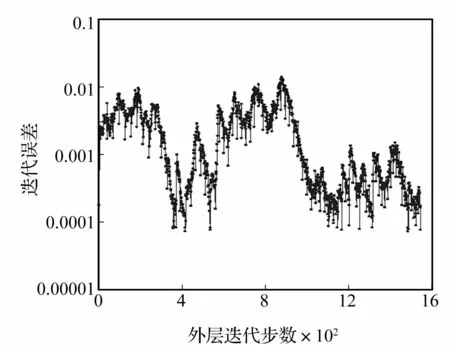
图3 1 025万自由度规模的迭代收敛历史

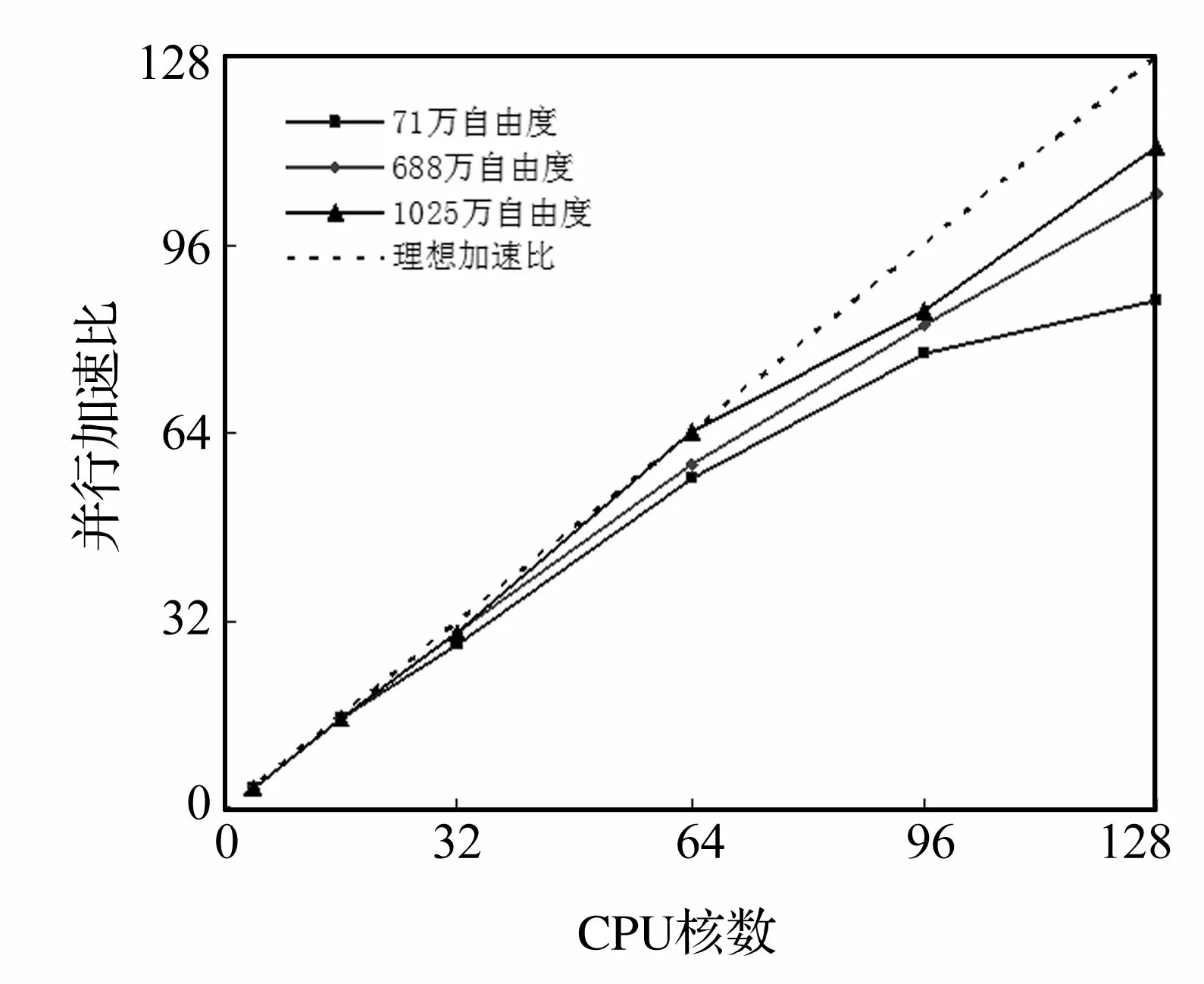
图4 三种不同规模模态分析的并行加速比曲线

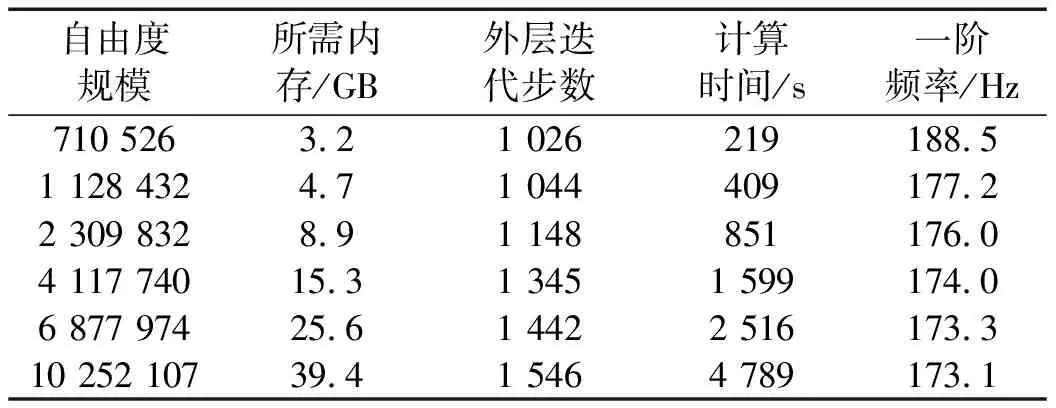
表4 128进程下不同自由度规模的并行计算结果统计

测试过程中发现各进程所占用内存基本一致，并行计算负载平衡良好。为进一步验证J-D算法的并行可扩展性，还就几种自由度规模进行了加速比测试。加速比是衡量并行计算程序性能和效率的基本评价方法，其定义如下：

Sp=Ts/Tp

(8)

式中，Sp为加速比，Ts为串行程序在并行计算机单处理器上的执行时间，Tp为相应并行程序在p个处理器执行所需的时间，Sp与p的比值即为并行效率。理想情况下，p个处理器上并行计算时间为串行计算时间的1/p，此时有Sp=p。但受到并行通信等因素的影响，在实际计算中Sp一般小于p，Sp越接近p，则说明并行程序性能越好，并行效率越高。图4给出了71万、688万和1 025万三种自由度规模在不同进程下测得的并行计算加速比曲线，经计算三种情形在128核时的并行效率分别为67.8%、81.9%和88.1%。从图4可以看出，三种规模在曙光5000A机群128个CPU核内的并行加速性能非常优异，三个加速比曲线接近线性加速，并且计算规模越大，曲线越靠近理想加速曲线，并行性能越好。究其原因，一方面J-D算法通过内-外层迭代求解特征值问题，避开了Krylov子空间类算法的矩阵分解运算，所涉及的运算主要是矩阵-向量积或向量之间的一些内积运算，不改变矩阵本身的结构特性，通信量相对较少；另一方面，随着计算规模的增大，各子区域边界自由度数相对子区域内部自由度数变少，从而各进程间的通讯计算量较分配到每个并行进程内部的计算量也相应变小，并行性能得以更好的提升。

4 结 论

本文针对大规模模态分析问题，对J-D算法开展了一系列适应性改进、程序实现和并行测试研究。通过这些研究可以发现：

(1)本文借助PANDA框架和特征值软件包所建立的并行计算体系完全可以满足大规模模态分析需求，对现有开源程序和数值计算软件包进行集成可以为大规模并行程序开发节省大量人力和物力。

(2)改进后的J-D算法能够很好地适应千万自由度以上规模的模态分析，具有内存占用少，并行可扩展性能优异等优点。通过选取不同的控制参数和施加谱变换技术，可以有效提高J-D算法外层迭代的收敛速度。

(3)本文在128核的并行机群上的测试结果表明，各种规模在最大CPU核数内均未出现计算拐点，即J-D算法可以继续向更多的CPU核数扩展，可以推断利用该算法并基于更高性能并行计算机上在10余分钟内解决千万自由度以上规模的模态分析问题是完全可能的。

参 考 文 献

[1]Bai Z, Demmel J, Dongarra J, et al. Templates for the solution of algebraic eigenvalue problems：A practical guide[M].SIAM, Philadelphia, 2000.

[2]Saad Y, Numerical methods for large eigenvalue problems[M].Halsted Press, Div. of John Wiley &Sons, Inc., New York, 1992.

[3]Watkins D S. The matrix eigenvalue problem：GR and Krylov Subspace Methods[M]. SIAM, Philadelphia, 2007.

[4]Lanczos C, An iteration method for the solution of the eigenvalue problem of linear differential and integral operators[J].Journal of Research of the National Bureau of Standards, 1950, 4(45):255-282.

[5]Calvetti D，Reichel L，Sorensen D C. An implicitly restarted lanczos method for large symmetric eigenvalue problems[J].ETNA, 1994,2:1-21.

[6]Wu K， Simon H. Thick-restart lanczos method for symmetric eigenvalue problems[R]. Report 41412, Lawrence Berkeley National Laboratory,1998

[7]Crouzeix M, Philippe B, Sadkane M. The davidson method[J].SIAM Journal on Scientific Computing,1994,15(1):62-76.

[8]Sleijpen G L G，Van der Vorst H A, A Jacobi-Davidson iteration method for linear eigenvalue problems[J]SIAM Journal on Matrix Analysis and Applications, 1996, 17(2):401-425.

[9]Shi G M，Wu R，Wang K Y. Discussion about the design for mesh data structure within the parallel framework[R].9th World Congress on Computational Mechanics and 4th Asian Pacific Congress on Computational Mechanics, Sydney, Australia, 2010.

[10]Hernandez V，Roman J E，Vidal V，et al. SLEPc：a scalable and flexible toolkit for the solution of eigenvalue problems[J].ACM Trans. Math. Softw, 2005, 31(3):351-362.

[11]Barrett R，Berry M，Chan T F，et al. Templates for the Solution of Linear Systems：building blocks for iterative methods[M].SIAM, Philadelphia, PA, USA, 1994.

[12]Meerbergen K， Spence A， Roose D. Shift-invert and cayley transforms for detection of rightmost eigenvalues of nonsymmetric matrices[J]BIT Numerical Mathematics, 1994, 34(3)：409-423.

[13]Hernandez V，Roman J E，Tomas A, et al. A survey of software for sparse eigenvalue problems. Tech. Rep[M]SLEPc Technical Report STR-6, Universidad Politecnica de Valencia, 2012.

[14]Arbenz P， Hetmaniuk U L，Lehoucq R B，et al. A comparison of eigensolvers for large-scale 3D modal analysis using AMG-preconditioned iterative methods, Internat[J]. Numerical Methods in Engineering，2005, 64(2)：204-236.

[15]Karypis G，Kumar V. Metis-a software package for partitioning unstructured graphs, partitioning meshes, and computing fill-reducing orderings of sparse matrices. version 4.0[R]Tech. Report, University of Minnesota, Minneapolis, 1998.