求解扩散方程的二级四阶隐式Runge-Kutta方法

开依沙尔·热合曼,努尔买买提·黑力力

(新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046)

求解扩散方程的二级四阶隐式Runge-Kutta方法

开依沙尔·热合曼,努尔买买提·黑力力

(新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046)

对空间变量应用中心差分格式和紧致差分格式离散,时间变量采用二级四阶Runge-Kutta方法,构造求解扩散方程的精度为O(τ4+h2)和O(τ4+h4)的两种绝对稳定的隐式差分格式,讨论稳定性,并将数值试验结果与Crank-Nicholson格式进行比较,数值结果表明该方法是求解扩散方程的有效数值计算方法之一.

扩散方程;紧致格式;二级四阶Runge-Kutta方法;两层隐格式;Crank-Nicolson格式

0 引言

考虑如下齐次边界条件的一维扩散方程:

(1)

扩散方程是一类描述物理量随时间的扩散和衰减规律的抛物型微分方程.自然环境、工程设备及生物机体中的许多物理现象,诸如气体的扩散、液体的渗透、热的传导以及半导体材料中杂质的扩散等都可用扩散方程来描述.由于物理问题本身的复杂性,其精确解往往不容易求得,研究其数值求解方法具有非常重要的理论意义和工程应用价值.

目前求解该问题的差分格式主要有显式格式、隐式格式、Crank-Nicolson格式[1-3]和其他一些格式[4-11].文献[4-5]中空间变量用中心差分格式离散化,时间变量分别用四阶经典R-K方法和修正梯形公式得到了精度分别为O(τ4+h2)和O(τ3+h2)的数值格式.文献[6-7]中空间变量用四阶紧致差分格式离散化,时间方向用Crank-Nicolson格式构造非齐次和齐次扩散方程的绝对稳定的差分格式,文献[8-9]中中空间变量用中心差分格式离散化,时间变量用修正Crank-Nicolson格式得到一维和二维热传导方程绝对稳定的显式差分格式.文献[10]中空间变量用中心差分格式离散化,时间方向用三次C1样条方法构造精度为O(τ4+h2)的绝对稳定的两层隐式格式.文献[11]在文献[10]的基础上对空间变量用四阶紧致差分格式离散化,对时间方向用三次C1样条方法构造热传导方程和对流扩散方程的精度为O(τ4+h4)的绝对稳定的两层隐式格式.

受上述文献的启发,对空间变量分别用中心差分格式和紧致差分格式离散化,时间变量应用二级四阶隐式Runge-Kutta方法构造扩散方程的精度分别为O(τ4+h2)和O(τ4+h4)的两种绝对稳定的隐式差分格式,并讨论其稳定性,数值值结果与Crank-Nicolson格式进行比较,验证了本文中方法的有效性.

本文由3部分组成,第一部分是扩散方程的二级四阶隐式Runge-Kutta方法的构造,第二部分讨论格式的稳定性,第三部分给出具体的数值算例,并将结果与Crank-Nicolson格式和准确值进行比较,最后给出文章的结论.

1 本文中格式的构造

1.1二级四阶隐式Runge-Kutta对常微分方程组

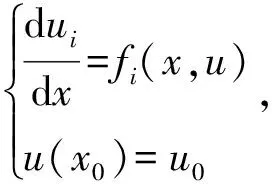
(2)

的二级四阶隐式Runge-Kutta格式为(3)式

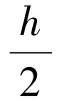
(3)

二级四阶隐式Runge-Kutta法是A-稳定的[3].

1.2两种差分格式的构造方程(1)式对x变量分别用中心差分和四阶紧致格式离散,对t变量保持不变,

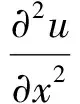
(4)

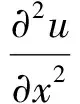
(5)

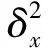
把(4～5)式代入方程(1)式将得到如下常微分方程组(6～7)式

(6)

(7)

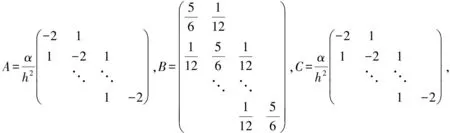
矩阵B严格对角占优阵,因此非奇异.

常微分方程组(6～7)式用二级四阶隐式Runge-Kutta格式(3)式得到本文中的格式(8～9)式

(8)

(9)

其中M=B-1C,格式(8)式为精度O(τ4+h2)格式,而(9)式为精度O(τ4+h4)格式.

下面讨论格式(8)和(9)的稳定性.

2 稳定性分析

证明格式(8～9)式的稳定性之前,先引入两个引理:

引理1[2]:若A是一个N阶三对角阵,

其中a,b,c是实数,bc>0,则A的特征值为

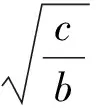
由引理1直接得出矩阵A的特征值为

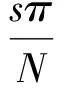
由此推出λA≤0.

引理2假设λi(i=1,2,…,N-1)为矩阵B-1C的特征值,xi(i=12,…,N-1)为其相应的特征值向量,则特征值λi为实数,且λi≤0.

引理2的证明下面观察B-1C的特征值:

由此推出λi≤0.

定理1本文中差分格式(8)式和(9)式是绝对稳定的.

定理1的证明分别记格式(8)式和(9)式的特征值为λ(8)和λ(9),则

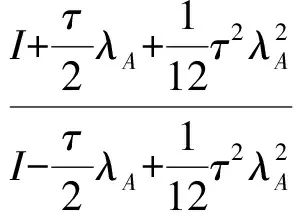
其中λA和λi为矩阵A和B-1C的特征值.

由引理1和引理2得知λA≤0,λi≤0所以λ(8)≤1,λ(9)≤1,由此推出迭代格式(8)式和(9)式的谱半径小于等于1,因此迭代格式(8)式和(9)式是绝对稳定的.

3 数值实验与结果分析

给出下面的常系数一维扩散方程初边值问题:

该方程的准确解为u(x,t)=sin(πx)e-π2t

表1给出了当h=0.1,τ=0.1,T=1时的Crank-Nicolson格式和格式(8)式和(9)式的绝对误差比较,最后一行给出了最大误差,从表1可以看出格式(8)式和(9)式误差比Crank-Nicolson格式小.

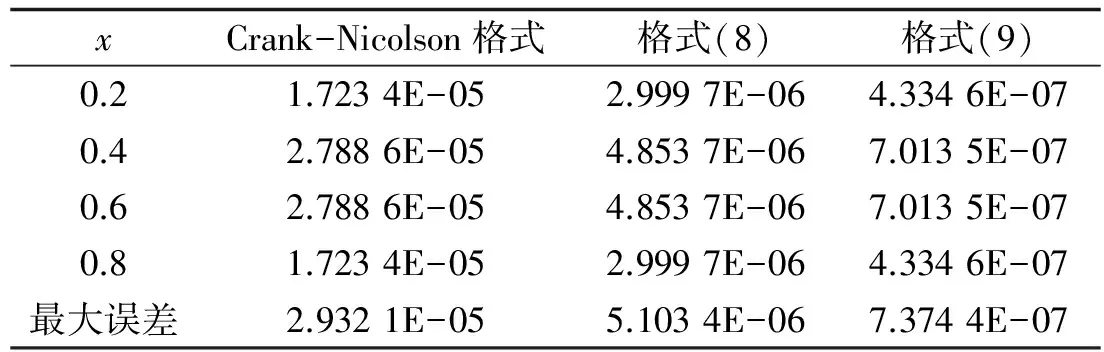
表1 h=0.1,τ=0.1,T=1时绝对误差比较

表2给出了空间步长取不同值时的Crank-Nicolson格式和格式(8)式、(9)式的最大误差和收敛阶比较,从表中可以看出Crank-Nicolson格式和格式(8)对空间变量二阶收敛,而格式(9)对空间变量四阶收敛.

表2 当τ=0.001,T=1时的不同空间步长的收敛阶的比较

表3给出了时间步长取不同值时Crank-Nicolson格式和格式(8)式、(9)式的最大误差和收敛阶比较,从表3可以看出格式(8)式、(9)式对时间变量四阶收敛.

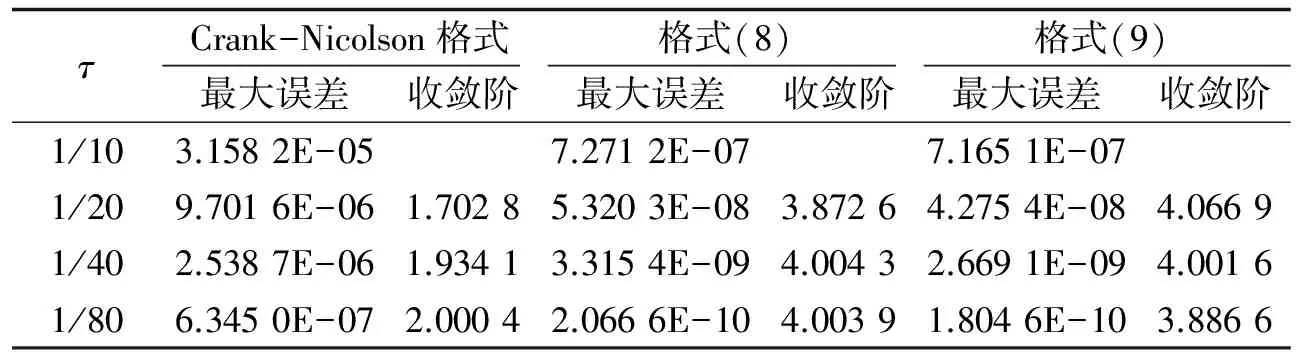
表3 当h=0.005,T=1时的不同空间步长的收敛阶的比较

图1给出了h=0.1,τ=0.1,T=1时Crank-Nicolson格式、格式(8)式、(9)式与准确解进行比较,从图1中可以看出本文中格式(8)式和(9)式比Crank-Nicolson格式更接近于准确解.

4 结论

对空间变量分别采用二阶中心差分格式和四阶紧致差分格式进行离散话,对时间变量采用二级四阶隐式Runge-Kutta公式,对扩散方程构造了截断误差分别为O(h2+τ4)和O(h4+τ4)的两种两层绝对稳定的隐式差分格式.试验结果表明理论上的截断误差和数值试验结果相符合.表1～3和图1的数值试验结果说明格式(8)式、(9)式与Crank-Nicolson格式相比,更接近于准确解.

图1 h=0.1,τ=0.1,T=1时的3种格式与准确解比较

[1] 陆金甫,关治.偏微分方程数值解法[M].2版.北京:清华大学出版社,2004.

[2] Smith G D. Numerical solution of partial differential equations(finite difference methods)[M]. Third edition. Oxford: Oxford University Press,1996.

[3] 李瑞霞,何志庆.微分方程数值方法[M].广州:华南理工大学出版社,2005:38-43.

[4] 开依沙尔·热合曼.一种一维扩散方程三阶精度的半离散隐式差分格式[J].甘肃联合大学学报,2009,23(1):33-36.

[5] 开依沙尔·热合曼.求解一维热传导方程的一种半离散差分格式[J].新疆师范大学学报,2007,26(3):142-46.

[6] 田振夫.非齐次热传导方程的高精度隐式格式[J].宁夏大学学报,1996,17(3):34-38.

[7] 葛永斌,田振夫.求解扩散方程的一种高精度隐式差分方法[J].上海理工大学学报,2005,27(2):107-111.

[8] 阿不都热西提·阿不都外力.修正局部Crank-Nicolson法对于二维热传导方程的应用[J].计算数学,1997,19(3):267-276.

[9] Abuduwali A, Sakakihara M, Niki H. A local Crank-Nicolson method for solving the heat equation[J]. Hiroshima Mathematical Journal,1994,24(1):1-13.

[10] Sallam S, Anwar M N, Abdel-Aziz M R. Unconditionally stableC1-cubic spline collocation method for solving parabolic equations[J]. International Journal of Computer Mathematics,2004,81(7):813-821.

[11] Mohebbi A, Dehghan M. High-order compact solution of the one-dimensional heat and advection-diffusion equations[J]. Applied Mathematical Modelling,2010,34(10):3071-3084.

(责任编辑 赵燕)

Twostagefourth-orderRunge-Kuttamethodforsolvingdiffusionequation

KAYSAR·Rahman, NURMAMAT·Helil

(School of Mathematics and System Sciences, Xinjiang University, Urumqi 830046, China)

We applieed central finite difference approximation of second order and compact finite difference approximation of fourth order for discrediting spatial derivatives, and used two stage fourth order Runge-Kutta method in time direction derived two unconditionally stable implicit schemes in which local truncation error wasO(τ4+h2) andO(τ4+h4), then discussed its stability. Numerical experiment was compared with Crank-Nicolson scheme. Numerical experiment results showed that it was an efficient method for solving diffusion equation.

diffusion equation; compact scheme; two stage fourth-order Runge-Kutta method; two-level implicit scheme; Crank-Nicolson method

2014-02-13

国家自然科学基金项目(11261057)和新疆维吾尔自治区教育厅高校科研计划重点项目(XJEDU2012I01)资助

开依沙尔·热合曼(1978-),男,副教授,E-mail:kaysar2001@sina.com;努尔买买提·黑力力,通信作者,副教授,E-mail:nurmamat@gmail.com

1000-2375(2014)05-0476-05

O241.8

A

10.3969/j.issn.1000-2375.2014.05.019