抗病毒药物治疗人类免疫缺陷病毒1型(HIV-1)的分数阶模型研究

崔周进,陈桂东

(1.江苏海事职业技术学院基础部,江苏 南京 211170; 2.解放军理工大学理学院数学教研中心,江苏 南京 211101)

0 引 言

在对传染病的诸多研究中，数学模型是检验理论和定量评估猜想与结论的实验工具.自20世纪80年代首例艾滋病病例被发现以来，很多学者在HIV动力学的建模上进行研究，绝大多数的数学模型基于整数阶微分方程.例如，文献[1]中建立了如下HIV动力学模型:

(1)

其中x和y分别表示t时刻未感染和已感染的CD4+T的数量，z表示t时刻血浆中病毒粒子的数目.系统中所有的系数均为非负数，s是CD4+T细胞的生成率，μ是人均死亡率，β是CD4+T细胞被病毒感染率，ε是被感染细胞的人均消失率，c为感染细胞与病毒的转化率，而γ是病毒粒子的死亡率.

近几十年来，由于在科学和工程众多领域中的广泛应用，分数阶微积分(也即任意实数或复数阶的微积分)受到人们越来越多的关注和重视.目前分数阶微积分已成为一个研究热点，并在多个领域得到了应用，如松弛、振荡、扩散和输运理论、生物组织、高分子材料的解链、混沌与湍流、随机游走、统计与随机过程、粘弹性力学及非牛顿流体力学等．这些领域的应用研究又反过来促进了分数阶微积分理论研究的进一步发展.随着分数阶微分方程的快速发展，很多研究者尝试用分数阶微分方程建模[2-4].研究表明，在传统的整数阶方程不能建模的现象中，分数阶方程为此提供了可能性.分数阶与整数阶模型最大的区别在于分数阶模型拥有记忆，而免疫反应的主要特征恰恰包含记忆.为此Arafa等[2]建立如下HIV感染与免疫系统相互作用的分数阶动力学模型：

(2)

其中Dα是α阶Caputo微分算子，0<α1,α2,α3<1.作者利用广义Taylor公式与同伦分析法，研究了系统(2)的简化模型的解.本文的主要目的是在前期研究的基础上，探讨分数阶系统(2)的平衡点的稳定性，并通过数值模拟验证理论分析的结果.

1 动力学分析

分数阶的导数有许多定义[5-6]，例如Riemann-Liouville定义、Gruunwald-Letnikow定义、Caputo定义、Miller-Ross定义等等.为了方便起见,首先给出本文中采用的Caputo微分算子.

定义1(Caputo定义的分数阶导数)

(3)

其中n=[α]+1，Γ为Gamma函数.

Caputo定义由于其Laplace变换公式和整数阶导数的Laplace变换公式具有相同的形式, 因而在控制理论中广泛采用.本文研究分数阶线性系统的稳定性, 采用Caputo分数阶导数定义是合适的.

在平衡点E1=(s/μ,0,0)处，系统(2)的Jacobian矩阵为

那么E1点处对应的特征方程为

在平衡点E2点处对应的特征方程为

λ3+a1λ2+a2λ+a3=0，

定理11)若D(P)>0，则E2局部渐近稳定当且仅当a1>0,a1a2>a3>0.

2)若D(P)<0，a1≥0,a2≥0,a3>0，0.5<αi<2/3，则E2局部渐近稳定.

3)若D(P)<0，a1>0,a2>0,a1a2=a3，0.5<αi<1，则E2局部渐近稳定.

4)若D(P)<0，a1<0,a2<0，αi>2/3，则E2不稳定.

2 数值模拟

图1 α1=0.55，α2=0.6，α3=0.65时的相位图

治疗药物会影响产生病毒颗粒的感染细胞的死亡率. 但是因为药物可能不是100%有效，因此只有部分受感染的细胞将恢复到未感染类.文献[2]给出模型(2)中典型的参数取值，取s=0.272，μ=0.001 36，ε=0.33，γ=2，β=0.000 27，c=50，带有如下初值条件x(0)=200,y(0)=0,z(0)=1，则平衡点E2=(48.89,0.6228,15.57)，a1=2.34，a2=0.012 96，a3=0.002 77，D(P)<0，a1>0，a2>0，a3>0.根据定理1可得，当0.5<αi<2/3时，平衡点E2局部渐近稳定.相位图被用来确定系统的动力学行为，借助于Adams-Bashforth-Moulton预估校正算法，利用Matlab软件可以得到模型(2)在不同阶导数下的相位图.图1是模型(2)中分数阶导数分别取成α1=0.55，α2=0.6，α3=0.65时的相位图；图2是模型(2)中分数阶导数取成α1=α2=α3=0.6时的相位图；图3是模型(2)中导数取为α1=α2=α3=1.0时的相位图，通过图形可以验证上述结论的正确性.

图2 α1=α2=α3=0.6时的相位图

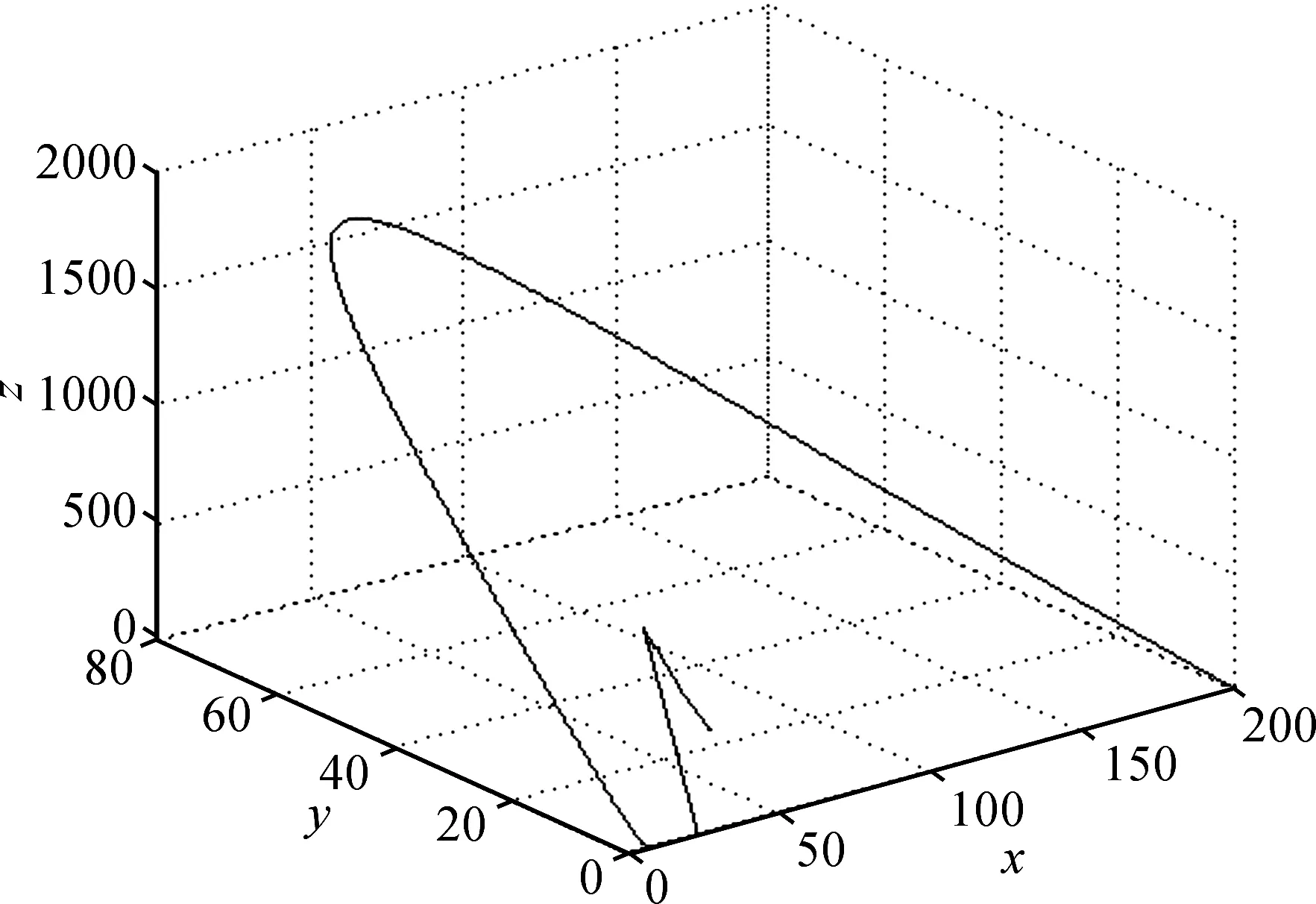
图3 α1=α2=α3=1.0时的相位图

3 总 结

传染病动力学是对传染病进行理论性定量研究的一种重要方法，是根据疾病的发生及在种群内的传播、发展规律，以及与之有关的社会等因素，建立能反映传染病动力学特性的数学模型.通过对模型动力学性态的定性、定量分析和数值模拟，来分析疾病的发展过程，揭示流行规律，预测变化趋势，分析疾病流行的原因和关键因素，寻求预防和控制的最优策略，为防治决策提供理论依据.在生物学中，研究人员发现，生物细胞膜具有分数阶的电子传导性，因而归类为分数阶模型；另外，需要特别强调的是分数阶微分算子与记忆有着重大关联，已经证实由分数阶微分方程建立的某些生物学模型比整数阶更有优势．随着分数阶微分方程的发展，分数阶模型更加向实际靠拢.本文中所利用的分数阶的Routh-Hurwitz准则，Adams-Bashforth-Moulton预估校正算法可以推广到类似的模型的研究中去.关于分数阶系统的动力学性质，例如分数阶传染病模型平衡点的存在性和稳定性，分数阶微分系统阶数如何影响模型的动力学性态，分数阶时滞传染病模型的最优控制问题，并给出分数阶动力系统控制的条件，这些都是下一步研究所关注的方向.

[1]Tuckwell H C, Wan F Y M. Nature of equilibria and effects of drug treatments in some simple viral population dynamical models[J]. IMA J Math Appl Med Biol,2000，17:311-327.

[2]Arafa A A M, Rida S Z, Khalil M. The effect of anti-viral drug treatment of human immunodeficiency virus type 1(HIV-1) described by a fractional order model[J]. Applied Mathematical Modelling,2013,37:2189-2196.

[3]Cui Z J, Mao Z S, Yang S J,etal. Approximate analytical solutions of fractional perturbed diffusion equation by reduced differential transform method and the homotopy perturbation method[J]. Mathematical Problems in Engineering,2013,Article ID 186934.

[4]Cui Z J, Yu P N, Zong W. Dynamical behaviors and chaos in a new fractional-order financial system: proceeding of the Fifth International Workshop on Chaos-fractals Theories and Applications[C].Dalian:5th IWCFTA,2012:109-113.

[5]Podlubny I. Fractional differential equations: vol.198 of Mathematics in Science and Engineering[M]. San Diego, Calif：Academic Press,1999.

[6]Hilfer R. Applications of fractional calculus in physics[M]. Singapore：World Scientific,2000.

[7]Ahmed E, E1-Sayed A M A, E1-Saka H A A. On some routh-hurwitz conditions for fractional order diferential equations and their applications in lorenz，rssler，Chua and Chen systems[J]. Physics Letters A,2006,358:1-4．

[8]Faieghi M R, Delavari H. Chaos in fractional-order Genesio-Tesi system and its synchronization[J]. Commun Nonlinear Sci Numer Simulat,2012,17(2):731-741．