时空某些基本特征的新探索与时空多样性

张一方

(云南大学 物理系，云南 昆明 650091)

0 引言

狭义相对论的时空，由运动决定.广义相对论的时空，由质量、引力决定.这是几何时空.福克就说：“物质的不同属性(广义质量等)决定相应不同时空的几何性质，几何性质又决定相应物质的运动”[1].

笔者在简述中外时空思想、牛顿的经典时空理论、法拉第的场和相对论的时空观后，由此引入相对-绝对时空理论.然后结合已知理论，主要讨论了时空观的某些新的发展前沿和可能的发展方向：空间及时间的对称性及其破缺，时空量子化，泛相对论和泛时空理论，量子纠缠态，时间箭头，分维、复数维时空及其高维时间等[2].

由相对论中可知：1)时间完全是时空统一的第4维，则可逆；并且可以对应各种领域中的熵减[3-9].2)时间如果不可逆，则时空统一的第4维应该有所不同，不可能仅是光锥.

首先应该发展时间的数学，即时间箭头的数学.对相对论是更准确的时间矢量几何：

(1)

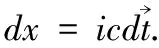
1 时空、四矢的对称性

表1 时空、四矢的对称性

四者纵统一为pi=hki=h/λi，Noether定理，对粒子是质量m、寿命τ对称[10,11]，及笔者提出的从狭义相对论和量子论必然得到的定量关系：能量和空间中同一地点的时间间隔成正比，和时间中同一瞬时的空间间隔成反比[10,12]：

E∝dt, E∝1/dt.

(2)

公式(2)分别在类时、类空区域，都是第4分量.应该研究广义相对论和量子力学中二者各相应的区域.引力场中，对同一瞬时能量

E=m0c2g00(dx0/ds)=m0c2g00(dx0/dl).

(3)

与dx0成正比，与dl成反比.动量无静止态，所以只在类空区域中，p、dl都是矢量分量，此时二者成正比.

2 力场中时钟的快慢和某些效应

爱因斯坦认为引力场中时钟变慢[13].Pauli称为引力场中时间膨胀(dilatation)[14].Rosser也认为引力场中时钟较慢[15].坦盖里尼得到引力场中钟慢[16]

ΔtA(1+gL/c2)=ΔtB

(4)

高度不同的时间不同，离地面越远钟越快.这是一种广义相对论效应，也是实验结果[17].它与笔者的结论一致，Δt变大，质增，尺缩，并且与能量成正比，与能量守恒有关.朗道提出引力场中时间是[18]

(5)

其中φ<0.斥力场中φ>0，所以虽然仍是g00，但斥力场中钟快.这联系于引力加速或减速，或都在引力场中即朝向(进入时加速)或离开引力场时减速，与方向有关.而斥力场中相反.类似在电磁场中可以是钟慢(对相反电荷)或钟快(对相同电荷)；对强弱相互作用分别是钟慢和钟快.

相同的变速系，导致引力场或斥力场；二者在相反的方向.势能都是减少.既等价于引力场，又等价于斥力场，则时间间隔是变大或变小值得研究.加速时势能(广义)变为动能，按照狭义相对论运动时间变慢(大)，设为正向；减速时动能(广义)变为势能，按照狭义相对论运动时间变快(小)，设为负向.但势能等价于引力场，引力时间的改变应该相反.

这联系于单摆、简谐振动是周期运动，运动时间也应该周期变化，但始终大于、等于0；引力时间可能周期相反.变化率不一定相同，则是二者的叠加；变化率相等则为常数.这又涉及双生子，加减速场，但总有运动，所以钟慢.

如果加速对应引力场，减速对应斥力场，则可能与曲率的正负相关.其中光速c变大或变小.加速时惯性(动)质量增大，按照等价原理引力质量也增大，a=H(引力场强).减速时惯性(动)质量减小，按照等价原理引力质量也减小.按照等价原理，任何非惯性系等价于引力场，所以应该是弯曲时空、非Euclid几何.电荷导致能量，又E=mc2，所以有相应的质量，如Δm=eφ/c2.

引力场中实验表明质增钟慢，二者成正比.引力场中势能减少，1)如果总能不变，则静能+动能与dt成正比时质增钟慢；dt与总能成正比，则钟相同.2)如果静能不变，则总能减小，dt与总能成正比则钟快.

(6)

既与dx0有关，又与dl有关.如果

(7)

则与时空间隔成正比、反比.

狭义相对论可以包括电磁场，其本身只有光子，时空一般不弯曲.但光子-光子相互作用时，时空应该也不是平直的.这样就必须修改狭义相对论.同时有电荷必有质量、引力场；而且大质量电荷吸引小质量电荷也不相对，以质量大者为主；而质量相同时，仅有两个荷电不同者完全相对；但是有多个时是多体问题，出现复杂性.在外场中加速度a=(e/m)H.

3 时空的相对-绝对性

惯性运动及其狭义相对论效应是完全相对的.但一进入非惯性系及等价的引力场就不相对了，就是相对于惯性系及真空(无引力场)是绝对的.时钟佯謬也说明绝对性.时空相对-绝对，则原理相对-绝对.有物质在广义相对论中就是相对-绝对原理.时空相对性，对应对称性；相应于类规范理论.

相对方面表现为纯数学的协变性，形式相同，及广义相对性原理.绝对性方面表现为差异性，在局部时空中有一个特别简单，同时相互之间是绝对的，导致对Euclid空间仅是局部扰动.相对-绝对原理取极限，无法判断差别，就是完全相对的相对性原理；其数学表述可以是秦元勋的最小质能时空参考系，即质心系在相对论下的推广.一个系统中质心所在点∑mivi/∑vi是绝对的，相对其静止的参考系就是最优越的，绝对不变的；即质心系相对优越.近似时就为2log10(m2/m1).这必须与发展广义相对论和量子论相结合.

Minkowski时空是平直的相对的；相应于狭义相对论不考虑引力场时具有精确的对称性、相对性.Riemann时空是弯曲的绝对的；相应于广义相对论必考虑引力场，质量大的弯曲性、引力场大，质量小的趋向质量大的，所以对称性(相对性)自发破缺；广义相对论仅仅具有近似对称性，如等价原理.此时单个质量产生绝对的绝对性，包括相对于背景辐射，等价原理的局域性；多个质量产生相对的绝对性，以质量大者为主.

只有相对于背景辐射的运动(对应于真空期待值，自发破缺对称性)才是绝对运动本身.但是两个或多个物体之间的运动却有相对的绝对性.不同地方的苹果都落地，但地球同时向不同地方的苹果运动却是荒谬的.

时空相对-绝对性，对应对称性自发破缺；相应于类Higgs场.在一定的边界、初始条件(对应极早期宇宙)下，Higgs场，sigma介子(相应于Dirac海)导致真空期待值不为0，且不相同，粒子等有不同质量，就有弯曲性不同的引力场，这相应于秦元勋方法.这不同于平直时空，而且对称性(相对性)自发破缺，具有绝对性.

二者结合就是相对-绝对时空[2].牛顿绝对性表现为同时性、时间等的绝对.时空的相对性表现在相对性原理，即运动的相对性和相对论中；绝对性表现为惯性系的可定义，惯性和非惯性运动的可区分.二者结合就有惯性系比非惯性系相对优越，对不同相对-绝对时空，运动-静止也是相对-绝对的.广义相对论中一定有相对-绝对性.福克就认为广义相对论中无相对性原理，但有协变性[1].在同一层级相对，在不同层级绝对；类似非标准分析.由数理逻辑应可以证明时空的相对-绝对性.20世纪60年代末以来有人放弃相对性原理，回到绝对空间；或改造和推广相对论体系的基本原理和概念.

规范理论能够描述自然界的所有基本力[19].Higgs (3K)场的特性：在真空中不为0(对应于真空背景3K)，其效应是提供一个特殊的参考系，它叠加于广义相对论对称性空间.这就具有绝对性.Heisenberg铁磁物质理论有完全的几何对称性，所有方向都相同.但物质磁化时有一个轴(如磁化方向)就不同.在外场中对称性破缺，如Zeeman效应或Stark效应，都是归为动力学.真空是完全对称的，相对的.但引入质量(相应于Higgs场)对称性破缺.一方面质量有相对大小就有绝对性；从大质量到小质量的方向，或大质量物体的引力场方向就对应于特殊轴.另一方面，无质量或质量可以忽略的真空背景(相应于3K)相对于有质量的空间也是优越的绝对系.这是结合最新的物理理论.P.W.Bridgman主张以绝对时间无操作意义代替其不存在的说法.现代宇宙学重新引进宇宙时间，其是优越的时间尺度，具有绝对的意义；并测出地球相对于“绝对空间”的绝对速度.

惯性运动基于绝对时空，也要求存在绝对时空.而惯性运动具有四个特点：相对的，近似的，也是方便的，有用的.时空也如此.爱因斯坦感到必须驱逐威胁其相对性的惯性系，把相对性原理贯彻到底，才能完全抛弃绝对时空，也就必然导致广义相对论.而广义相对论又必然肯定时空在某些方面的绝对性.牛顿力学，相对论，量子力学及一切物理学都区分惯性、非惯性系，所以也区分绝对、相对时空.只有承认不平权，有差别就必然有相对优越的相对-绝对时空.

超弦家Brain Greene提出：引力为0的虚拟太空就等效于绝对时空.他们提出用相互关系取代时空.对宇宙大爆炸，时空有起点.普适的宇宙时间可以存在于均匀的各向同性的宇宙背景中，如基于背景辐射的大爆炸起始时间.对大质量恒星，黑洞是终点.

4 量子时空，时空的多样性及时空对称性的破缺

量子力学时空及量子时空，由此联系于真空、粒子时空.量子论是时空与空间尺度、能量量子有关.进一步应与时间尺度、各种量子有关.这又联系于量子时空.最一般时空应与各种具体条件有关.

进一步发展分形及其推广的复维等时空.基于质能时空的关系dt=E/F=t2-t1，能量E=E0(mc2)+E'恒大于0，则t2>t1，时间不可逆.基于发展Dirac的负能态得到的最完备的对称结构，笔者提出负能量对应负物质，其主要特征是与所有正物质之间都是斥力[20-23].这样正负物质通常是两类拓扑分离的区域，是不可见的，因此负物质可以作为暗物质最简单的候选者.对暗物质最近提出的幻影(phantom)就是负物质.

对负物质、负能量t2-t1<0，时间反向不可逆.只要能量恒正或恒负，时间都不可逆.此时不可逆性是物质世界的本性.只要时间可正可负(如正负物质混合)时间就可逆.这对应于CPT定理.特别CT不守恒，正物质多于负物质，联系于T不可逆.如果正负物质相等，则时间可逆.世界湮灭为真空(场)，而真空(场)对应于时间可逆.质量可正可负[24]对应于dt、dl可正可负.质量等轴双曲线对应于狭义相对论，LT及GLT的等轴双曲线.

多时空体系[10]类似Anaximander的多种多样形式原始实体互相联系，互相转化；退化时统一.有不同的源，不同的守恒量，不同的场就有不同的时空体系.泛狭义相对论自动从完全相对的狭义相对性原理必然导致一个绝对速度ch必然恒定的原理[10,12].这是相对性与绝对性的统一.ch≡c说明世界的统一性，ch不一定是c则说明世界的多样性和多时空体系.ch的物质性联系于不同的物质背景；ch可以由光子推广到其他波和粒子.广义相对论从完全相对的广义相对性原理、协变原理导致绝对的时空弯曲，从绝对的mg=mi导致相对性的等价原理.广义相对性原理或广义协变性也包含绝对性，即其中的不变性，ds不变.物质决定时空，非Euclid几何，度规引力场的统一和绝对的场方程.

空间中的双缝多宇宙可以发展为时间中的双缝多宇宙

(8)

r=k1t1+k2t2,

(9)

k越大，t发生得越早.这与超光速意义相同.如果为双曲线，

(10)

结论相同，ch越大，t越小，但出现±和双解.由此可以预测事件前后的事，所以高维空间、时间可以联系于预测、超心理学、易经等.这是高维、分维时空结合多时空体系.

分维时空具有标度变换的不变性.但时间不再有平移不变性，空间无均匀性、旋转不变性，如此宇称、宙称、旋称不成立，相应的能量、动量、角动量不守恒.这又对应于PCT等变化，PEP破缺等基本问题.

藏密中提出“时间的层次性”，对应高维、分维时间及量子力学的不同叠加态.进一步即空间的层次性及时空层次性.对应多时空体系、多世界宇宙.它们之间就是虫洞及时空隧道.Simon Donaldson(1995-1996)利用Yang-Mills方程证明四维Euclid空间R4有无数微分结构与其标准结构不同.R4应推广为R3+C，即3实1虚的物理空间.这对应四元数、环、不可对易性及Markov过程、半群.

对人生与时空，第四维就是生命.超时空对应活动领域、生命价值.意识的时间、空间都具有特殊性.时空的多样性数学上相应于1956年J.W.Milner在7维球面上找到28种不同的微分结构和1982年以后S.Donaldson等证明4维Euclid空间可以有无穷多种微分结构.

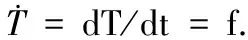
四维时空强调了时空的统一、一致性，但忽略了时空的不同性.时间是单向流动的.如此时空理论应该发展.在对称性中引入对称性破缺、时间方向性，群中引入半群.相应地，P、T等各种时空对称理论都应该有所不同.时空均匀对应能量-动量守恒；推广则为T、P破缺.空间各向同性对应角动量守恒；推广则有旋称破缺.时间的方向性对应熵增；相应的空间有方向就对应宇称P不守恒.Weisskopf已经提出应该重新区分时空[27].其实有相空间，却没有相时间.

时空等价互补原理联系于时空对称统一.如x=ct，则宇宙空间尺度反映宇宙时间尺度.狭义相对论是四维时空，时间和空间概念彼此密切联系.但时间有一维性、方向性等特性.两方面结合应该是一个三维存在的演化.

如果时空完全对称，则时间的一切性质可以推广到空间的一切性质，反之亦然.时间箭头→空间有方向性；空间全息→时间循环.假如不能推广则对称性破缺.因此时间类似空间推广为分维、复维等[25,26].时间、空间对称都有标度性.宇宙学中时间和空间是有区别的.局域的惯性参考系是一个相对优越的宇宙学参考系.

时间上的稳定对应于空间上的均匀；时间上的周期对应于空间上的周期.量子生物学Schrodinger方程导致时间节律、周期性.更一般量子力学、泛量子论[28-32]都导致时间周期性.输运、双曲方程及流体近似时导致空间周期性；

(11)

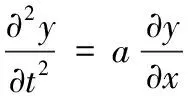
(12)

可导致时间周期性.而这是

(13)

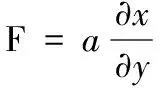
Whitrow等认为

(14)

(15)

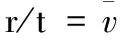
理论可以分为ds不变和ds可变两类.时间与时空维数发展，相对论及与时空相关的各种理论，如量子力学、量子场论、天文学、宇宙论等就应发展.特别是狭义相对论应用于具有分维的固液气体等时就应该有所不同.这可以结合’t Hooft量子化，粒子的砂-海绵分形模型(FSSM)[10]，相变等理论.

目前的理论确定宏观和微观并不是相对的.因为h是确定的，量子论也只对微观成立.但对统计力学，宏观和微观是相对的，分维的自相似性结构也是相对的.而且统计力学与量子场论对应，所以统计力学中二者相对，高能时统一，则量子场论高能时也已统一，宏观和微观二者也应统一.如果相对，则应有标度性，即宇宙量子论[28-31].这可以结合泛量子论.它也是发展到不同时空范围的“相对论”.

[1]B.A.福克著，周培源等译.时间、空间和引力的理论[M].北京：科学出版社，1965.

[2]张一方.时空观的某些新发展和相对-绝对时空理论[J].湖南城市学院学报.2008,17(2):41-47.

[3]张一方.孤立系统的内部机制和热力学第二定律局限性的新探索[C].熵、信息与交叉科学.喻传赞等编.昆明:云南大学出版社.1994. 53-60.

[4]Chang Yi-Fang. Possible decrease of entropy due to internal interactions in isolated systems[J]. Apeiron. 1997, 4(4):97-99.

[5]Chang Yi-Fang. Entropy, fluctuation magnified and internal interactions[J]. Entropy. 2005, 7(3): 190-198.

[6]Chang Yi-Fang. “Negative temperature” fallacy, sufficient-necessary condition on entropy decrease in isolated systems and some possible tests in physics, chemistry and biology[J]. International Review of Physics. 2012,6(6):469-476.

[7]Chang Yi-Fang. Chemical reactions and possible entropy decrease in isolated system[J]. International Journal of Modern Chemistry. 2013,4(3):126-136.

[8]Chang Yi-Fang. Possible entropy decrease in biology and some new research of biothermodynamics[J]. NeuroQuantology. 2013,11(2):189-196.

[9]Chang Yi-Fang. Grand unified theory applied to gravitational collapse, entropy decrease in astronomy, singularity and quantum fluctuation[J]. International Journal of Modern Applied Physics. 2013,3(1):8-25.

[10]张一方.粒子物理和相对论的新探索[M].昆明：云南科技出版社.1989.184-238. Chang Yi-Fang, Phys.Abst.,93(1990)No1371.

[11]Chang Yi-Fang. From emergence string to mass formulas of hadrons and symmetric lifetime formulas of hadrons[J].International Review of Physics. 2012,6(3):261-268.

[12]Chang Yi-Fang. Extension and complete structure of the special relativity included superluminal and nutrino-photon with mass[J].International Journal of Modern Theoretical Physics. 2013,2(2):53-73.

[13]A.爱因斯坦著，李灏译.相对论的意义[M].北京:科学出版社.1961.

[14]W.Pauli, Theory of Relativity[M]. New York: Pergamon Press. 1958.

[15]W.G.V.Rosser, An Introduction to the Theory of Relativity[M]. London: Butterworths. 1964.

[16]F.R.坦盖里尼著，朱培豫译.广义相对论导论[M].上海:上海科学技术出版社.1963.

[17]秦荣先,阎永康.广义相对论与引力理论实验检验[M].上海：上海科学技术文献出版社.1987.

[18]L.朗道,E.栗弗席兹著，任朗,袁炳南译.场论[M].北京:人民教育出版社.1959.

[19]G. ’t Hooft, Gauge theories of the forces between elementary particles[J]. Scie.Am. 1980, 242,(6):90-116.

[20]张一方.量子力学和相对论的结合、不相容及发展[J].云南大学学报. 2008,30(1):41-46.

[21]张一方.相对论与量子力学的关系及理论的发展[J].商丘师范学院学报. 2008,24(12):57-61.

[22]Chang Yi-Fang. Negative matter, dark matter and theoretical test[J]. International Review of Physics. 2011,5(6): 340-345.

[23]Chang Yi-Fang. Field equations of repulsive force between positive-negative matter, inflation cosmos and many worlds[J]. International Journal of Modern Theoretical Physics. 2013, 2(2):100-117.

[24]列.布里渊著，刘松林译.相对论的新观点[M].贵阳：贵州人民出版社.1987.

[25]张一方.数学,物理中分维的发展和分维时空理论[J].大自然探索.1991,10(2):49-54.

[26]Chang Yi-Fang. Fractal relativity, generalized Noether’s theorem and new research on space- time[J]. Galilean Electrodynamics. 2010,21(6):112-116.

[27]V.F.Weisskopf, Contemporary frontiers in physics[J]. Science. 1979,203(4377):240-244.

[28]张一方.Titius-Bode定则的发展,天体量子论和泛量子理论[J].云南大学学报.1993,15(4): 297-303.

[29]Chang Yi-Fang. Development of Titius-Bode law and the extensive quantum theory[J]. Physics Essays. 2002,15(2):133-137.

[30]张一方.泛量子理论的发展及其在生化和物理中的应用[J].吉首大学学报.2006.27(5): 34-38;48.

[31]Chang Yi-Fang. Quantized phenomena in astronomy and astronomic quantum theory[J]. International Journal of Sciences. 2013,2:58-73.