高斯定理在万有引力场中的推广及应用

谢谦，唐卫斌，刘俊

（商洛学院 电子信息与电气工程学院，陕西商洛 726000）

高斯定理是电磁学中的重要定理之一，其推导过程是从库伦定律[1]而来，在力学中，牛顿万有引力定律和库伦定律，形式上相似[2-4]，既然通过库伦定律可推导出电学中的高斯定理，那么类似的也可以从万有引力定律推导出力学中的高斯定理，通过高斯定理，可以简便解决引力场中的相关问题。

1 万有引力定律与库伦定律的比较

这两个定律形式上完全相同，如下：

其中r是场点到源点的位矢，因万有引力只能是引力，且质量只能取正值，故公式前是负号。

可见，只要把电荷电量换成质点质量，把k换成G，则两式形式上完全相同，只是电荷有正有负，库伦力有引力也有斥力，而质量只能取正值，作用力只能是引力。

2 力学中的高斯定理

在电磁学中通过库伦定律可推导出高斯定理[1]：

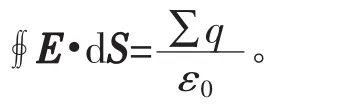
既然万有引力与库伦定律形式上相同，即两者都为平方反比定律，且引力场强度与电场强度定义相同，经对比可得力学中的高斯定理为：

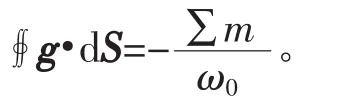
即引力场强度g对任意闭合面S的积分（引力场通量），等于这个闭合面所包围总质量的负值除以 ω0。

闭合面S的方向是其外法线方向。

下面对其从特殊到一般，分步来加以证明。

2.1 通过包围质点m的同心球面的引力场通量都等于

以质点m所在处为中心，任意半径r做一球面（图1），根据万有引力定律，在球面上各点引力场强度大小一样，，方向沿半径向内指向球心。在球面上，任取一面元dS，其外法线是沿半径方向向外的，即n和g夹角为 θ=π，所以通过的引力场通量为：

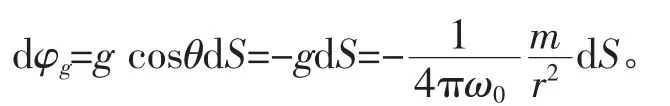
通过整个闭合球面的引力场通量为：

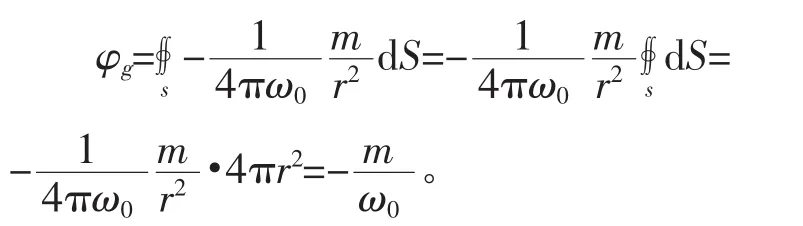
这一结果与球面半径无关，之所以会有这一结果，是和平方反比定律分不开的。

图1 包围质点m的同心球面

2.2 通过包围质点m的任意闭合面S的引力场通量都等于

在闭合面S内以点电和q所在处O为中心做一任意半径的球面S″，根据2.1可知，通过此球面的引力场通量为，由于引力场分布的球对称性，该通量均匀的分布在4π球面度的立体角内，因此在每个元立体角dΩ内的引力场通量是，如果把这个立体角的锥面延长，使它在闭合面S上截出一个面元，设dS到质点m的距离为r，dS的法线n与矢径r的夹角为θ，如图2，则通过dS的引力场通量为：

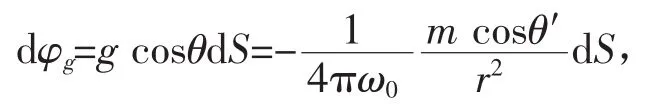
式中dScosθ′=dS′是dS在垂直于矢径方向的投影面积，所以

由此可见，通过面元dS的引力场通量和通过 S″上与 dS对应的面元dS″的引力场通量一样，所以通过整个闭合面S的引力场通量都必定和通过球面S″的引力场通量一样，等于。

2.3 通过不包围质点m的任意闭合面S的引力场通量都等于0

如果闭合面不包围质点，即质点位于闭合面外，如图3所示。

这时从m所在点看来，整个曲面S可分为图式的S1和S2两部分，其中S1部分对质点m所张的立体角Ω1取正值，S2部分对质点m所张的立体角Ω2取负值，由于两者的绝对值相等，所以通过整个闭合面S的g通量为：

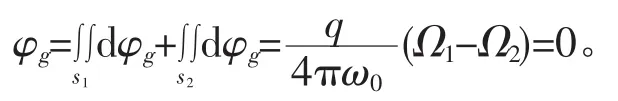
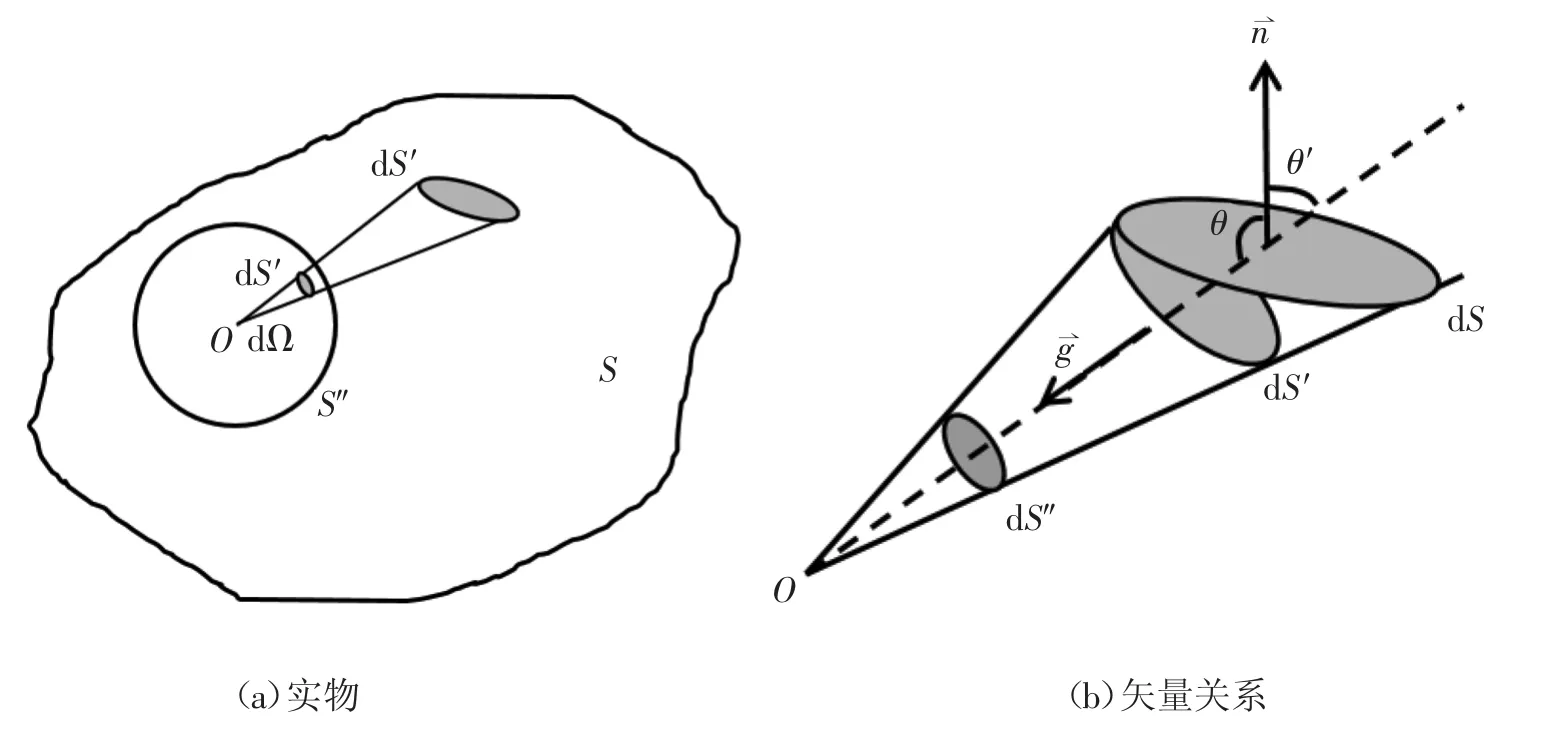
图2 包围质点m的任意闭合面

图3 闭合面不包围质点

2.4 多个质点的引力场通量，等于他们单独存在时的引力场通量的代数和

它们在闭合面S法线方向的投影gn=gn1+g2n+...，

（图略）

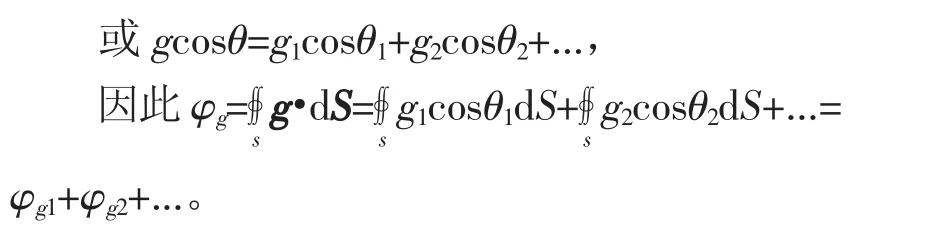
设有 m1、m2、…、mk个质点，其中 1→n 个被高斯面所包围，第n+1→k个在高斯面外，

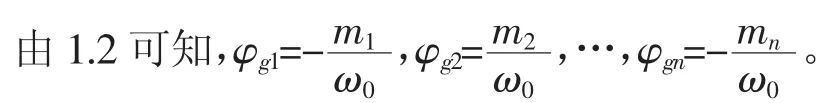
由1.3可知，S外部质点的通量φgn+1=φgn+2=…=φgk=0，

因此k个质点同时存在时，通过S的总通量：

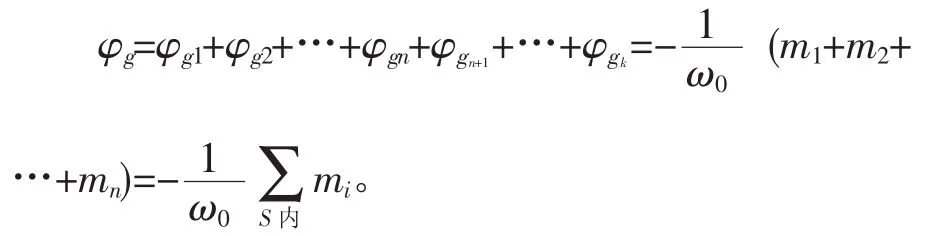
至此，引力场中的高斯定理证毕。

3 引力场中高斯定理的应用

对于质量具有某种对称性均匀分布的物体，用高斯定理可求其引力场强度。

3.1 与“填补法”相结合求解空腔内的引力场

在一密度为ρ半径为R的球形天体内有一半径为r（r＜R）的球形空腔（图4），证明该空腔内的引力场是均匀的。

图4 空腔球体内的高斯面及矢量

该问题涉及到一类典型问题的求解方法：填补法[5]。假设用与球体相同的密度为ρ的物质均匀填充该空腔，则构成了一个半径为R，密度为ρ的实体球体。根据引力场的独立作用原理，该半径为R的实体球在半径为r的实体球内的引力场等于半径为r的球O′与球O′以外部分在此产生的引力场强度之和。

球O′以外部分在O′内场强则为所求证，设为g，半径R的实体球在此的场强设为go，球O′在此的场强设为gO′，则：

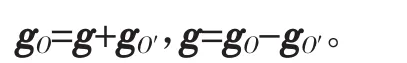
由于球O与球O′均为质量均匀的球体，故其产生的引力场强具有球对称性，即以各自球心为中心，任一半径为球面的高斯面上的场强大小相等，方向沿径向指向球心，对球O′内任一点P，分别以O、O′为中心，以OP、O′P为半径做一高斯面（图5），根据高斯定理，

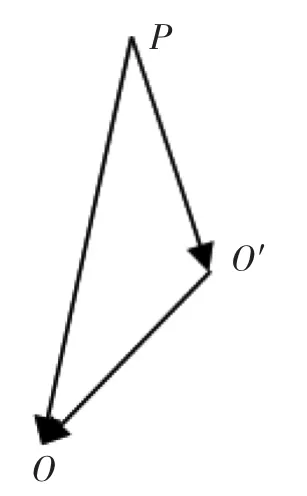
图5 矢量三角形关系图

3.2 地球内部隧道内质点的简谐运动问题

设想在地球表面的A、B两地之间开凿一长为L的直通遂道，在A处放置一质量为m的小球,小球在地球引力的作用下从静止开始在隧道内运动[6]。忽略一切摩擦阻力。试证明小球在隧道内做简谐振动，并由此求出小球的最大速度及从A运动到B所需的时间（图6）。

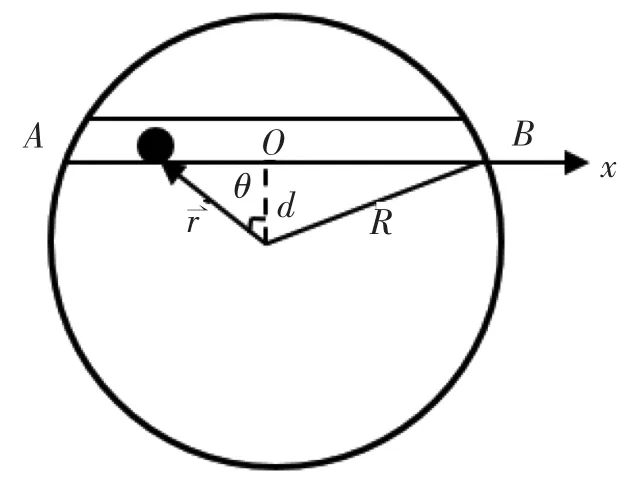
图6 地球隧道内质点的简谐振动

分析：如图6所示建立直角坐标系，根据引力场的高斯定理，小球所在位置x处的引力场强度为：

可见Fx与x成正比而方向相反，所以m是以O为平衡位置在隧道内做简谐振动。

下面求出其振动方程。

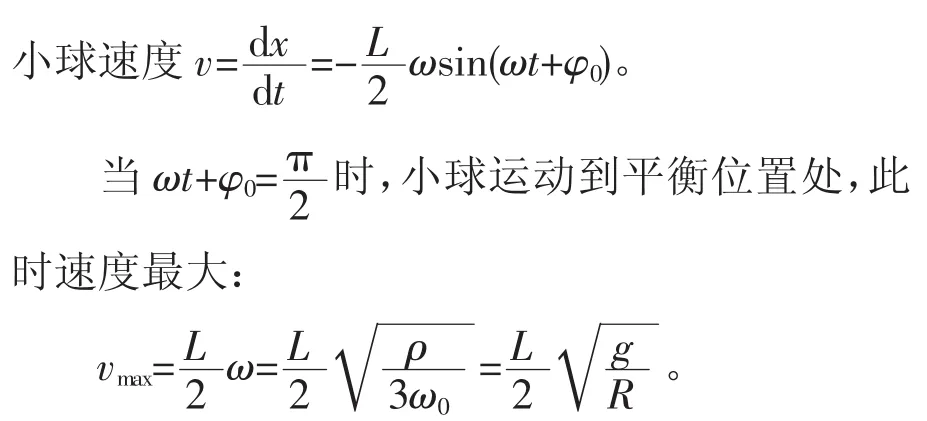
4 结语

通过对比万有引力定律与库仑定律，发现二者的相似性的规律，从而通过电学中的高斯定理，引申出引力场中的高斯定理，并加以证明其正确性。这有助于加深对引力场的理解，为引力场和静电场的某种联系提供了一种证据。这种引力场中的高斯定理为解决某些天体引力场提供了一种新的、简便的方法，在教学中有助于学生拓展思维，激发兴趣，从而提高学习能力[8]。