带固定参数的Monadic递归*
苏锦钿 余珊珊
(1.华南理工大学 计算机科学与工程学院,广东 广州 510640;2.广东药学院 医药信息工程学院,广东 广州 510006)
作为归纳数据类型[1]上最重要的一种计算模式,递归操作fold[2]在程序设计、推理、转换和优化等方面具有广泛的应用,并构成其他各种复杂的递归计算的基础,如原始递归、Course-of-Value 迭代、带参数的递归和累积递归等.但fold 一方面要求计算源中的元素必须具备相应的代数结构,无法包含额外的参数用于作为计算的输入;另一方面只适合于描述计算过程中所产生的确定性结果,无法包含其他各种计算副作用(如偏序、非确定性、异常、连续、交互式输入、交互式输出等).针对上述问题,Cockett 等最早在文献[3-4]中利用笛卡尔封闭范畴上的强函子提出了强范畴数据类型的概念,使得强归纳数据类型上的fold 可包含额外的参数,并将其作为函数式程序语言Charity 的基础.随后,Pardo[5-7]进一步对强归纳数据类型上带固定参数和累积参数的递归操作pfold 和afold 的范畴论性质及其计算律进行了分析.笔者在前期工作中也分析了强共归纳数据类型上带固定参数的共递归及其计算律[8-9],并将其扩展到hylomorhpism 中[10],同时还从双代数的角度探讨了归纳与共归纳数据类型、递归与共递归间的关系[11].上述研究都是针对强归纳或强共归纳数据类型上的纯函数,没有考虑计算过程中可能产生的副作用.
Fokkinga[12]结合monads 及集合范畴上的正则函子提出任意数据类型上的monadic 射和fold.Hu等[13]进一步将Fokkinga 的研究扩展到任意monads上.Meijer 等[14]则从函数式程序语言实现的角度探讨monadic fold 的应用.Pardo[15]也结合monads 给出包含计算副作用的monadic 共递归和hylomorphism的定义.在Pardo 和Meijer 的研究基础上,Ghani等[16]探讨了所有归纳数据类型上的build 结合子及其参数的归纳和monadic 构造.这些研究均没有考虑带参数且包含计算副作用的递归,也没有分析相应的范畴论性质及其代数计算律.
因此,文中在上述研究的基础上,结合范畴论中的monads 及伴随概念给出monadic 强归纳数据类型的定义及其monadic 强初始性的证明,并分析了其上带固定参数且包含计算副作用的递归操作的定义、性质及计算律,从而将Cockett 和Pardo 等对强归纳数据类型及Fokkinga、Hu 和Meijer 等对monadic 递归的研究融合在一起.
1 归纳数据类型和Monads
1.1 代数和归纳数据类型
下面首先给出代数的范畴论定义.
定义1 给定范畴C 和自函子F:C→C,F-代数定义为二元组(X,αX:FX→X),其中X 称为该F-代数的载体,αX称为该F-代数的基调.任意两个F-代数(X,αX)和(Y,αY)间的F-代数同态射f:(X,αX)→(Y,αY)是载体集上的射f:X→Y,且满足等式fαX=αYFf.
若代数函子F:C→C 存在初始代数,记为(μF,inF),则对于任意一个F-代数(X,αX),总存在从(μF,inF)到(X,αX)的唯一F-代数同态射foldF(αX):μF→X,即满足等式foldF(αX)inF=αXFinF.
操作foldF(αX)是由基调αX所确定的迭代射,在函数式程序语言中常称为fold[2]或catamorphism[17].
为保证代数函子总是存在相应的初始代数,文中只考虑以下的代数函子[15].
定义2 范畴C 上的代数函子F:C→C 是由以下的函子归纳构造而成:
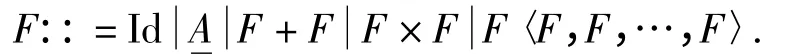
式中:Id 表示标识函子;A 表示A 上的常量函子;F +F 表示函子间的共积,F×F 表示函子间的积;F〈F,F,…,F〉(或记为F〈Fi〉)表示F:Cn→C 与其他代数函子F1,F2,…,Fn的组合,且F1,F2,…,Fn均具有相同的元数.
Vene 在文献[18]中证明了若F 为ω-共连续的(例如保持ω-共极限),则对应的F-初始代数存在.对于分配范畴[19](如集合范畴或完全偏序范畴)来说,定义2 中的代数函子都是ω-共连续函子,因此其初始代数总是存在.
下面如无特别说明,均假定范畴C 为分配范畴,并用F 或G 等大写字母表示定义2 中的代数函子.
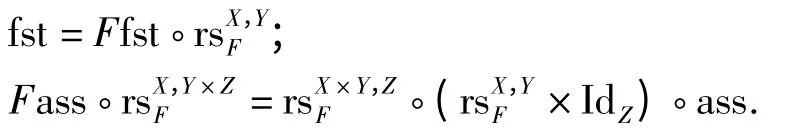
Kock 在文献[20]中证明了分配范畴C 上的定义2 中的代数函子都是强函子.
1.2 Monads
定义4 范畴C 上的monad 可表示一个Kleisli三元组(T,η,-*),其中T:为C 中对象间的映射,映射η 对于任意对象XC 有ηX:X→TX;提升函数-*对于任意射f:X→TY 有f*:TX→TY,且满足以下等式(即使得图1 中的所有图表满足交换条件):
(1)ηX*=IdTX;
(2)对于f:X→TY,有f*ηX=f;
(3)对于f:X→TY 和g:Y→TZ,有g*f*=(g*f)*.
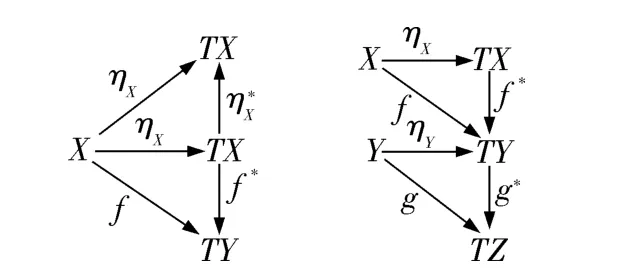
图1 Kleisli 三元组的图表交换Fig.1 Graph commutation of Kleisli triples
Monads 也可从范畴论的角度给出相应的定义.
定义5 范畴C 上的monad 定义为一个三元组(T,η,μ),其中T:C→C 为自函子,η:IdT 和μ:T2T 为自然转换,且满足等式μηT=μTη=Id 和μTμ=μμT.
称η 和μ 分别为该monad 的单位元和倍乘操作.容易验证(T,η,-*)和(T,η,μ)定义之间存在一一对应关系.为了便于讨论,文中有时候用monads的Kleisli 三元组定义,有时候用其范畴论定义.
例1 下面是部分典型的monads 结构.
(1)标识monad(Id,Id,Id):表示将一个类型映射到它本身.在计算意义上,标识monad 代表平凡的状态,即不进行任何动作并立即返回值.η 和μ 均为标识射.对于射f:X→X,f*也为标识射,将f 映射为自身;
(2)异常monad(Id +E,inl,[Id,inr]):表示计算可能成功并返回给定类型的输出值,也可能失败并返回类型为E 的输出值(E 为异常的集合).ηX=inl:X→X +E,μ=[Id,inr]:(X +E)+E→X +E;对于f:X→TY,f*=[f,inr]:X+E→X+E,使得f*(c)=c(cE)和f*(x)=f(x)(xX);若E 为1,则称其为部分monad(Id+1,inl,[Id,inr]);
(3)积monad(Id×S,〈IdX,e!X〉,Id×mr- ×Id):TX=X ×S 描述计算中包含了简单的输出处理或计算资源(如时间或空间),其中(S,e,m)为一个独异点,e:1→S 为单位元函数,m:S ×S→S 为S 上的二元函数.ηX=〈IdX,e!X〉:X→X ×S,μX=IdX×mr:(X×S)×S→X×S.对于f:X→Y×S 有f*=Id ×mrf×IdS,即f*(x,s)=〈fst(f(x)),m(snd(f(x)),s)〉(xX,sS).其中,!X:X→1 为任意元素对终结对象1 的射,r:(X×S)×S→X×(S×S)为交换元素位置的自然同构射.
类似地,还有许多其他的monads,如数组、状态、副作用、Input/Output、writer 和连续monad 等.
定义6 称范畴C 上的(T,η,-*)为强monad当且仅当T 为强函子,且同时满足以下等式:
(1)CA中的对象与C 中的对象相同;
(2)CA中任意两个对象X 和Y 之间的射为C中对象间形如f:X×A→Y 的射;
(3)CA中任意对象X 上的单位射为fst:X×A→X;
(4)CA中任意两个射f:X×A→Y 和g:Y×A→Z间的组合为gAf=g〈f,snd〉:X×A→Z.
若将C 看成是纯函数范畴,则CA就是描述了所有计算源中包含参数类型A 的计算范畴.
利用monad(T,η,-*)可将射f:X×A→Y 提升为fT=ηXf:X ×A→TY,从而描述了带固定参数A且产生副作用T 的计算.称形如f:X ×A→TY 的射为带固定参数的monadic 射.若(T,η,-*)为强monad,则fT可进一步提升为射f#=μYTf:TX ×A→TY,f#表示对fT的提升.
定义8 给定范畴CA及范畴C 上的一个强monad(T,η,-*),定义范畴CT为:
(1)CT中的对象与CA的对象相同;
(2)CT中的射为CA中射f:X ×A→TY 的提升fT=ηYf:X×A→TY;
(3)CT中任意对象X 上的单位射为CA中X 上单位射fst:X×A→X 的提升fstT:X×A→TX;
(4)CT中任意两个射f:X×A→TY 和g:Y×A→TZ 间的组合为gTf=g#〈f,snd〉=〈f,snd〉:X×A→TZ.
范畴CT描述了所有带参数A 且产生副作用的计算范畴,组合gTf 给出了计算结果及副作用在计算中的传递.显然,-T可看成从范畴CA到CT的一个函子,将范畴CA中的对象X 映射为自身XT=X,将范畴CA中的f:X ×A→Y 映射为对应的fT,将范畴CA中的射f:X×A→Y 和g:Y×A→Z 间的组合gAf 映射为范畴CT中的射(gAf)T=gTTfT.
Pardo 在文献[5]中定义了函子-^ :C→CA用于将C 中的f:X→Y 提升为f^=ffst:X×A→Y,将C 中射f:X→Y 和g:Y→Z 间的组合gf 提升为
定义9 给定范畴C 上的monad(T,η,-*)和自函子F:C→C,称自然转换 :FTTF 为F 对T 的分配律,当且仅当以下等式成立:
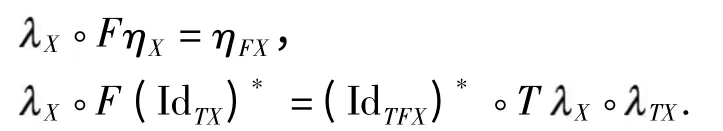
若分配律 存在,可定义函子F :CT→CT,将CT中的对象X 映射为X=FX,将f:X×A→TY 映射为f=XFf:FX ×A→TFY,将f:X ×A→TY 和g:Y×A→TZ 间的组合gTf 映射为F (gTf)=F gTF f:FX×A→TFZ.
2 Monadic 强归纳数据类型
为区别于一般的F-代数(X,αX:FX→X),将形如()的结构称为FA- 代数.任意两个FA-代数(X,φX)和(Y,φY)间的FA-代数同态射f:(X,φX)→(Y,φY)为射f:X ×A→Y,且满足f.若 射f:X→Y 满足fφX=φYFf ×IdA,则称f 为(X,φX)和(Y,φY)间的纯FA-代数同态射.由范畴C 上的所有FA-代数及其FA- 代数同态射可构成范畴Alg(FA).
类似地,将形如(X,φX:FX ×A→TX)的代数称为monadic FA-代数.给定强monad(T,η,-*)及分配律:FTTF,任意两个monadic FA-代数(X,φX)和(Y,φY)间的monadic FA-代数同态射为射f:X×A→TY,且满足f#〈φX,snd〉=φY#〈f,snd〉.若射f:X→Y 满足TfφX=φYFf×IdA,则称f 为(X,φX)和(Y,φY)间的纯monadic FA-代数同态射.由范畴C 上所有monadic FA-代数及其monadic FA-代数同态射可构成范畴AlgT(FA).
定义10 给定范畴Alg(FA)和AlgT(FA),定义函子L:Alg(FA)→AlgT(FA)为:
(1)L 将Alg(FA)中的FA-代数(X,φX)映射为AlgT(FA)中对应的L(X,φX)=(X,φ);
(2)L 将Alg(FA)中(X,φX)和(Y,φY)间的FA-代数同态射f:X×A→Y 映射为AlgT(FA)中(X,)和(Y,)间的monadic FA-代数同态射Lf=fT:X×A→TY;
(3)L 将Alg(FA)中任意对象X 上的单位射fst:X×A→X 映射为AlgT(FA)中对应的fstT:X×A→TX;
(4)L 将Alg(FA)中的FA代数同态射f:X×A→Y和g:X×Y→Z 间的组合gAf 映射为AlgT(FA)中对应的monadic FA-代数同态射组合L(gAf)=LgTLf.
由L 的定义可知L 保持单位射及射之间的组合关系.因此,L 确实为函子.
定义11 给定范畴Alg(FA)和AlgT(FA),定义函子V:AlgT(FA)→Alg(FA)为:
(1)V 将AlgT(FA)的monadic FA-代数(X,φX)映射为Alg(FA)中的FA- 代数V(X,φX)= (TX,X×IdA:FTX×A→TX);
(2)V 将AlgT(FA)的monadic FA-代数同态射f:X×A→TY 映射为Alg(FA)中的FA-代数同态射Vf=f#:TX×A→TY;
(3)V 将AlgT(FA)中任意对象X 上的单位射fstT:X×A→TX 映射为Alg(FA)中对应对象TX 上的单位射fst:TX×A→TX;
(4)V 将AlgT(FA)的monadic FA-代数同态射f:X×A →TY 和g:Y×A→TZ 间的组合gTf 映射为Alg(FA)中对应的FA-代数同态射组合V(gTf )=VgAVf.
命题1 L:Alg(FA)→AlgT(FA)和V:AlgT(FA)→Alg(FA)构成伴随关系且L 为左伴随,V 为右伴随.
证明 由L 和V 的定义可知存在自然转换ηX×fst:IdVL,使得对于Alg(FA)中任意的FA-代数同态射f:X×A→TY,AlgT(FA)中均存在对应的monadic FA-代数同态射g:X ×A→TY,并满足f=VgAηX×fst,如图2 所示.
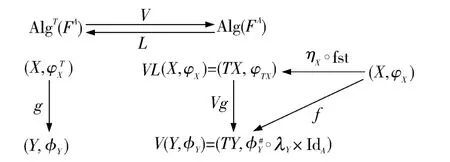
图2 函子L 和V 间的伴随关系Fig.2 Adjoint between the functors L and V
根据伴随关系的定义(见文献[21]中定义13.2.1)可知构成伴随关系,且L 为左伴随,V 为右伴随.证毕.
Pardo[5]证明了分配范畴上的强归纳数据类型具有强初始性,即(μF:FμF×A→μF)是范畴Alg(FA)中的初始代数.由于左伴随保持极限,因此L 将Alg(FA)中的FA-初始代数提升为AlgT(FA)中对应的monadic FA-初始代数,且保持其初始性.即(μF:FμF×A→TμF)是AlgT(FA)中的初始代数,且具有初始性.
定义12 称强函子F 的初始代数(μF,inF)为monadic 强初始的,当且仅当对于对象A,提升iFμF×A→TμF 是范畴AlgT(FA)中的一个初始对象.
即对于AlgT(FA)中的任意monadic FA-代数(X,φX),总是存在从(μF)到(X,φX)的唯一monadic FA-代数同态射f:μF ×A→TX,并称(μF,)是monadic 强初始的.
命题2 对于分配范畴上的代数函子F 及强monad(T,η,-*),若存在分配律:FTTF,则F-初始代数是monadic 强初始的.
证明 由命题1 可得.证毕.
由命题2 可给出monadic 强归纳数据类型的定义.
定义13 称一个归纳数据类型是monadic 强归纳类型当且仅当该归纳数据类型所对应的初始代数是monadic 强初始的.
3 带固定参数的Monadic 递归
定义14 给定强函子F:C→C、强monad(T,η,-*)和对象AC,对于任意一个monadic FA-代数(X,φX),带固定参数的monadic 递归pmfold,记为pmfoldF(φX):μF ×A→TX,是指满足以下等式的最小解:
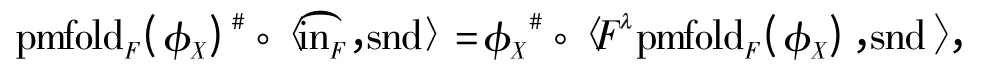
即使得图3 满足图表交换条件.

图3 pmfold 的定义Fig.3 Definition of pmfold
每一个pmfoldF(φX)可看成是在递归计算过程中计算源包含了参数类型为A 的元素,该参数的值在计算过程中保持不变,且所产生的计算副作用封装在T 中.
命题3 每一个fold 都可看成是计算过程中不使用参数且不产生任何计算副作用的pmfold.
证明 对于任意一个F-代数(X,αX),由定义14可知每一个foldF(αX):μF→X 相当于在计算过程中不使用参数A 且T 为标识monad 的pmfold,并满足:证毕.
命题4 文献[5]中的每一个pfold 都可看成是带固定参数但不产生任何计算副作用的pmfold.
证明 对于任意一个FA-代数(X,φX),由定义14 及文献[5]中pfold 的定义可知pfoldF(φX):μF×A→X 相当于T 为标识monad 的pmfold,并满足等式pfoldF(φX)T=pmfoldF(φTX).证毕.
命题5 文献[12]中的每一个monadic fold 都可看成是不使用任何参数的pmfold.
证明 对于任意一个monadic F-代数(X,αX:FX→TX),由定义14 及文献[12]中monadic fold 的定义可知每一个monadic fold([αX])T:μF→TX 相当于计算过程中不使用参数A 的pmfold,且满足等式证毕.由命题3- 5 可知pmfold 实际上给出fold、pfold[5]和monadic fold[12]的一种抽象描述.因此,它们的标识律、消去律和融合律等计算律在pmfold 中仍然成立.下面给出pmfold 上的部分典型计算律.
定律1(标识律) 每一个pmfold 满足等式:
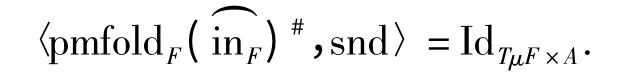
证明 由前面-^ 和-#的定义和定义14 容易验证为一个pmfold,且等于ηXfst.再由-#的定义可知IdTμF×A成立.证毕.
定律2(消去律) pmfold 满足:
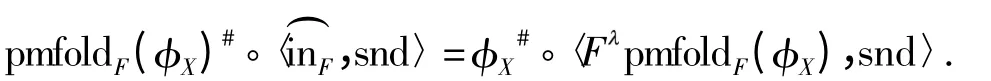
证明 由定义14 可得.证毕.
定律3(pmfold 与monadic FA-代数同态射融合律) pmfold 与monadic FA-代数同态射之间的组合仍是pmfold,即:f=pmfoldF(φX)∧g#〈φX,snd〉=〈F g,snd〉gTf=pmfoldF(φY).
证明 由前提可知图4 中的左右部分均满足图表交换条件.因此,整个图4 满足图表交换条件.

图4 pmfold 与monadic FA-代数同态射的融合律Fig.4 Fusion law for pmfold and monadic FA-algebraic homomorphism
类似地,可证明pmfold 与纯monadic FA-代数同态射之间的组合仍是一个pmfold.
定律4(pmfold 与纯monadic FA-代数同态射融合律) pmfold 与纯monadic FA-代数同态射之间的组合仍是pmfold:f=pmfoldF(φX)∧TgφY=φXFg×IdATgf=pmfoldF(φY).
定律5(pmfold-pmfold 融合律) 若存在自然转换子ρ:FG,将每个monadic GA-代数(X,φX)映射为对应的monadic FA-代数(X,φXρX×IdA),将每个monadic GA-代数同态射f:(X,φX)→(Y,φY)映射为对应的monadic FA- 代数同态射,则两个pmfold g= pmfoldG(φX)与f= pmfoldF(ρμG×IdA)间的组合仍是一个pmfold:
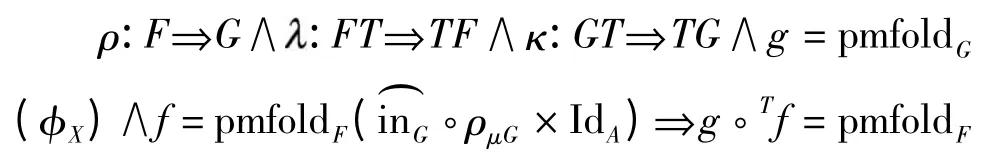
(φXρX×IdA),其中κ:GTTG 为函子G 对T 的分配律.
证明 由前提及函子和自然转换保持同态射的性质可知图5 中的左半部分以及右边的上下部分均满足图表交换条件,因此整个图5 满足图表交换条件.
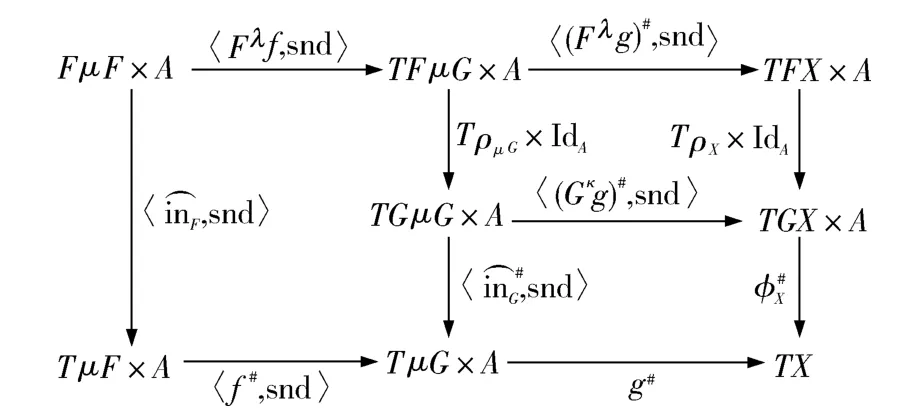
图5 pmfold 间的融合律Fig.5 Fusion law for pmfold
由于fold、pfold 和monadic fold 均可看成是pmfold 的一种特殊情况,因此pmfold 与它们间的组合仍是pmfold 操作.
利用上述各种融合律可以消去pmfold 在计算过程中所产生的中间数据,从而简化或优化程序的计算.
4 应用分析
4.1 归纳数据类型及fold 射
例2 程序语言中常用的树、数组和自然数等都是典型的归纳数据类型:
(1)设BTree(A)是以集合A 中的元素为标签的二元树,其上的构造子包括empty:1→X 和node:X ×A×X→X,即二元树BTree(A)可看成是代数函子RX=1 +X ×A ×X 所对应的初始代数(BTree(A),inR=[empty,node]).
(2)设[A]是所有包含集合A 中元素的有限数组的集合,其上的构造子包括:nil:1→[A]用于将数组初始化为空,cons:A×[A]→[A]用于将一个类型为A 的元素插入到给定的数组中,concat:[A]×[A]→[A]用于将两个数组串联成一个新的数组.显然,[A]就是程序语言中类型为A 的参数化数组,且为代数函子L=1 +A×X+X×X 的初始代数([A],inL=[nil,cons,concat]).
(3)自然数Nat 上的构造子包括:zero:1→Nat用于将自然数初始化为0,succ:Nat →Nat 为映射succk(0)asucck+1(0),用于对自然数加1,add:Nat×Nat→Nat 用于对两个自然数相加.则Nat 可看成是代数函子NX=1 +X+X×X 的初始代数(Nat,inN=[zero,succ,add]).
由归纳数据类型所对应的初始代数及其初始性可以给出许多fold 操作的定义.典型地,在函数式程序语言Haskell 中,数组类型[]上的各种折叠递归函数如fold、foldl 和foldr,以及针对非空数组的foldl1 和foldr1,都是基于[]的初始性和唯一性.
为了简单起见,一般直接将数组上的cons(a,l)表示为a:l,将concat(l,s)表示为l::s,将Nat 上的succ(p)表示为p+1,将add(p,q)表示为p+q.
4.2 pmfold 例子
下面以二元树上的遍历操作为例说明pmfold的应用.
例3 BTree(A)上的先序遍历操作traverse:BTree(A)×[A]→[A]×[A]定义为(其中b1,b2BTree(A),aA,l[A],s[A],且s 初始值为空数组[]):
(1)traverse(empty,l)=〈[],[]〉;
(2)traverse(node(b1,a,b2),l)=if isin(a,l)then
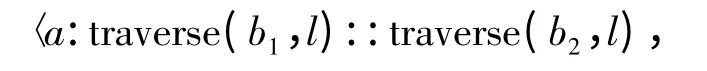
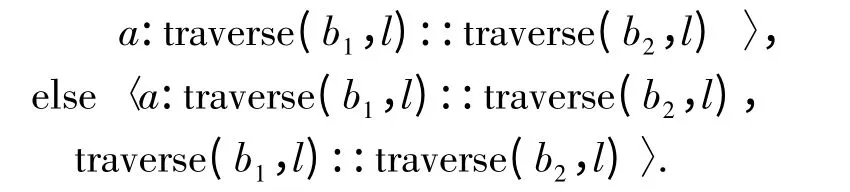
其中isin:A×[A]→1 +1 用于判断某个元素是否存在于给定的数组中,即isin(a,l)=if al then true else false.
显然,函数traverse 表示递归地对二元树中的所有节点进行先序遍历,并返回由这些节点所构成的数组;若节点存在于某个给定的数组中,则同时以数组的形式输出该节点.因此,traverse 可看成是增强了二元树上的先序遍历操作,允许在遍历的过程中添加某些约束条件(如根据某个给定的数组对树中的元素进行判断),并产生相应的输出和计算副作用.
根据定义14,traverse 是从monadic R[A]-代数A×BTree(A))×[A]→[A]×[A])到([A],φ[A]=[tnil,tconcat]:(1 +[A]×A ×[A])×[A]→[A]×[A])的pmfold 操作:pmfoldR(φ[A]):BTree(A)×[A]→[A]×[A],其中参数A 为数组[A],计算副作用封装在积monad(Id ×[A],η,-*)中,tnil(1,l)=〈[],[]〉,tconcat((b1,a,b2),l)=if isin(a,l)then〈a:b1::b2,a:b1::b2〉else〈a:b1::b2,b1::b2〉.
类似地,二元(或多元)树及图上的各种遍历(如中序或后序)操作都可扩展为相应的pmfold 操作.
例4 [A]上的函数filter:[A]×[A]→[A]×[A]定义为:
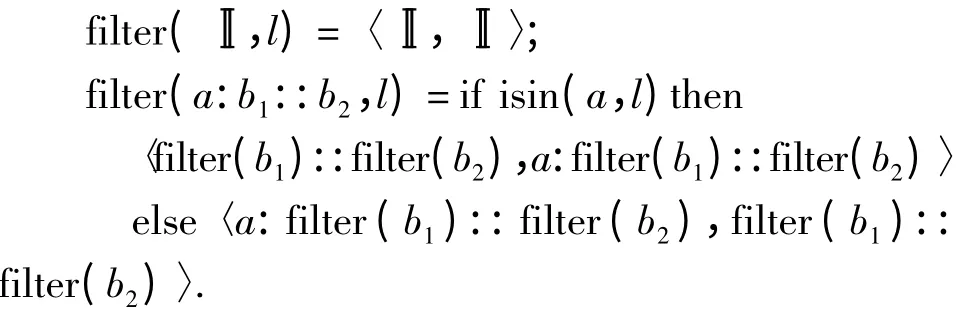
显然,filter 表示根据给定的数组参数对另一个数组中的元素进行过滤,并按原顺序返回剩余的元素,同时以数组的形式输出被过滤的元素.filter 可看成是从([A],φ[A]=[tnil,tconcat])到([A],φ[A]'=[fnil,fconcat])的monadic R[A]- 代数同态射,其中fnil([],l)=〈[],[]〉,fconcat(a:b1::b2,l)=if isin(a,l)then〈b1::b2,a:b1::b2〉else〈a:b1::b2,b1::b2〉.
用定律5 可将filter 和例3 中的traverse 函数融合在一起:ftree=filtertraverse:BTree(A)×[A]→[A]×[A],且ftree 定义为:
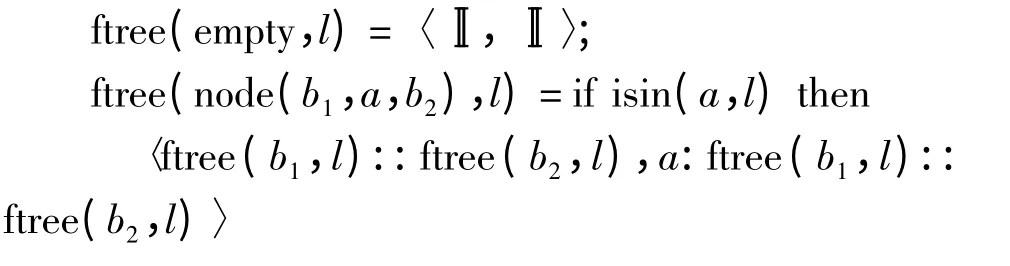
else〈a:ftree(b1,l)::ftree(b2,l),ftree(b1,l)::ftree(b2,l)〉.
函数ftree 表示对二元树进行先序遍历,且在遍历的过程中根据给定的数组对二元树中的元素进行过滤,并以数组的形式输出遍历结果和被过滤的元素.由定律5 可知ftree 为pmfold 操作ftree=pmfoldR(φ[A]').
5 结语
文中的主要贡献包括以下两点:
(1)证明了分配范畴上某些代数函子的初始代数在合适的条件上是monadic 强初始的,给出monadic 强归纳数据类型及其上带固定参数且包含计算副作用的递归操作pmfold 的定义;
(2)给出pmfold 上部分典型的范畴论性质及计算律,并分析了它与一般fold、pfold 和monadic fold之间的关系.
对带固定参数且包含计算副作用的递归操作的研究有助于进一步提高递归操作对复杂计算的描述能力,促进归纳数据类型在程序语言设计、转换及优化等方面的应用,并提高程序设计的模块性、隔离性和灵活性.
下一步将研究如何把文中工作扩展到包含累积参数的递归计算中,并探讨monads 对计算副作用的结构化描述以及comonads 对计算上下文的结构化描述间的有机结合.
[1]Greiner J.Programming with inductive and co-inductive types[R].Pittsburgh:Carnegie-Mellon University,1992:22-29.
[2]Gibbons J,Hutton G,Altenkirch T.When is a function a fold or an unfold?[J].Electronic Notes in Theoretical Computer Science,2001,44(1):146-160.
[3]Cockett J R B,Spencer D.Strong categorical datatypes I[C]∥Proceedings of International Meeting on Category Theory 1991.Ottawa:Canadian Mathematical Society,1991:141-169.
[4]Cockett J R B,Spencer D.Strong categorical datatypes II:a term logic for categorical programming[J].Theoretical Computer Science,1995,139(1):69-113.
[5]Pardo A.A calculational approach to strong datatypes[R].Oslo:Department of Informatics,University of Oslo,1997.
[6]Pardo A.Towards merging recursion and comonads[R].Utrecht:University of Utrecht,2000:50-68.
[7]Pardo A.Generic accumulations[C]∥Proceedings of IFIP TC2/WG2.1 Working Conference on Generic Programming.New York:ACM,2003:49-78.
[8]苏锦钿,余珊珊.广义共迭代及其计算律[J].华南理工大学学报:自然科学版,2012,40(9):62-68.Su Jin-dian,Yu Shan-shan.Generalised coiteration and its calculation laws[J].Journal of South China University of Technology:Natural Science Edition,2012,40(9):62-68.
[9]苏锦钿,余珊珊.带参数的共递归操作及其计算定律[J].计算机研究与发展,2013,50(12):2672-2690.Su Jin-dian,Yu Shan-shan.Corecursive operations with parameters and their computation laws[J].Journal of Computer Research and Development,2013,50(12):2672-2690.
[10]余珊珊,李师贤,苏锦钿.一种带参数的Hylomorphisms及其计算律[J].计算机研究与发展,2013,50(3):602-618.Yu Shan-shan,Li Shi-xian,Su Jin-dian.Hylomorphisms with parameters and its associated calculational laws[J].Journal of Computer Research and Development,2013,50(3):602-618.
[11]苏锦钿,余珊珊,抽象数据类型的双代数结构[J].华南理工大学学报:自然科学版,2011,39(12):44-50.Su Jin-dian,Yu Shan-shan.Bialgebraic structures for abstract data types[J].Journal of South China University of Technology:Natural Science Edition,2011,39(12):44-50.
[12]Fokkinga M M.Monadic maps and folds for arbitrary datatypes[R].Twente:University of Twente,1994.
[13]Hu Z,Iwasaki H.Promotional transformation of monadic programs[C]∥Proceedings of Fuji International Workshop on Functional and Logic Programming.Singapore:World Scientific,1995:196-210.
[14]Meijer E,Jeuring J.Merging monads and folds for functional programming[C]∥Proceedings of LNCS 925:Advanced Functional Programming.Berlin:Springer,1995:228-266.
[15]Pardo A.Monadic corecursion-definition,fusion laws,and applications[J].Electronic Notes in Theoretical Computer Science,1998,11(1):105-139.
[16]Ghani N,Johann P,Uustalu T,et al.Monadic augment and generalised short cut fusion [J].Journal of Functional Programming,2007,17(6):731-776.
[17]Meijer E,Fokkinga M,Paterson R.Functional programming with bananas,lenses,envelopes and barbed wire[C]∥Proceedings of Functional Programming Languages and Computer Architecture.Berlin:Springer,1991:215-240.
[18]Vene V.Categorical programming with inductive and coinductive types[D].Estonia:Institute of Computer Science,University of Tartu,2000:22-31.
[19]Walters R F C.Data types in distributive categories[J].Bulletion of the Australian Mathematical Society,1989,40(1):79-82.
[20]Kock A.Strong functors and monoidal monads[J].Archiv der Mathematik,1972,23(1):113-120.
[21]Barr M,Wells C.Category theory for computing science[M].2nd ed.Montréal:Centre De Recherches Mathematiques,1999.

