基于PLS和SVM的纸张抗张强度建模比较*

陶劲松 杨亚帆 李远华

(华南理工大学 制浆造纸工程国家重点实验室，广东 广州 510640)

造纸过程中，抗张强度不足会引发断纸、生产中断和大量能源的浪费，通常为了保持连续生产和抗张强度质量满足客户需求，抗张强度会超过标准生产，这又导致原料和能源损失严重.然而目前的抗张强度预测模型主要为机理模型，同时没有抗张强度的在线测量仪表，测量都需进行破坏性试验，所以造纸厂对其控制存在较大的滞后性、偏差性［1］.

现在的抗张强度模型可分为3 大类:Page 机理模型［2］及其改良模型［3-4］;Shear-lag 机理方程［5］及其改良模型［6］;线性回归及神经网络预测模型.Page模型、Shear-lag 模型及其改良模型中的大部分参数需要通过实验测得，预测精度较低，实用性不强.王宝玉［7］使用SPSS 软件建立的抗张指数多元线性回归方程及Navita 等［8］使用BP 神经网络建立的模型解决了模型预测精度低的问题，但模型使用的参数与生产中参数类型差距仍然较大，并没有解决实际应用中的问题.由于这些模型精度低和生产指导意义有限，现有的这3 类模型均未应用于在线预测.

偏最小二乘法(PLS)由Wold 等［9］在1983年首次提出，它是一种多因变量对多自变量的多元统计数据分析方法，能够将主成分分析、典型相关及多元线性回归分析有机地结合起来，尤其适用于变量多重相关性、小样本等情况下的多对多线性回归分析.而Vapnik［10］提出的支持向量机(SVM)训练过程遵循结构风险最小化原则，结构参数在训练过程中根据样本数据自动确定，无过拟合现象，它通过解一个线性约束的二次规划问题得到全局最优，不存在局部极小值问题，SVM 计算规范，易于实施.PLS 和SVM 均擅长处理多元相关变量的回归问题，且预测精度较高，实用性强.

由于生产变量数目众多，变量间存在一定的相关性，因此建模方法需要涵盖这两方面.文中采用PLS与SVM 这两种常用方法建模，通过比较并简化这两种方法的预测效果，选出生产中预测抗张强度的最佳模型，从而为在线预测纸张抗张强度创造前提条件.

1 模型的建立

1.1 建模方案

抗张强度作为大多数纸种共有的性能指标，对其进行建模研究具有更高的普适性.为更准确地在生产中预测纸张的抗张强度，应选择最佳抗张强度模型.文中将从某瓦楞纸厂采集数据，使用偏最小二乘法与支持向量机建模，并比较两者的精度，再通过筛选相关系数的方法进行模型简化和精度比较.

1.2 实验仪器及数据采集软件

使用iFIX 5.0 采集该厂DCS 系统数据，并将数据存放于Proficy Historian 中，查询采集浆料相对应的操作参数;采用Lorentzen ＆ Wettre 公司抗张强度测量仪测试纸张的抗张强度.

1.3 数据采集

以某瓦楞纸厂一条生产线为对象，采集该生产线生产信息，包括生产浆料性质、抄纸过程参数及成纸抗张强度.由于实际生产中DCS 采集标签有几百个，为了能够在模型中体现有效影响因素，而不受多余因素干扰，重点采集影响抗张强度的纤维自身强度性质、纤维间结合强度和纤维的排列分布相关的参数.通过流送成形、干燥施胶系统等从分布式控制系统(DCS 系统)以及质量控制系统(QCS 系统)中选择影响因素，并根据浆料性质测量相应的打浆度和定量，共选择30 个变量(见表1)构成数据库，选取某生产线2013-12-30—2014-01-13 的数据进行建模分析.

1.4 数据预处理

由于数据采集的时间为正常生产时间，纸张样本的生产时间与模型参数采集的时间一一对应，因此数据没有缺失和异常值;因所采集数据的量纲不同，需要对数据进行标准化处理.标准化处理能够消除各个变量在量纲上的差异对分析结果造成的影响，并可以提高分析算法的效率.数据标准化见式(1)和(2)，数据标准化后变量xj均值为0，方差为1.

其中，

式中，i (i=1，2，…，n)为样本个数，j (j=1，2，…，m)为变量个数.

表1 选取的参数Table 1 Selected parameters

1.5 偏最小二乘法建模

文中采用的是单因变量偏最小二乘法［11］，方法如下.

设自变量与因变量表达式为X=(x1，x2，…，xm)，Y=(y).标准化处理后，表达式变为矩阵E0=［e1e2… em］，F0=［f1］.

在E0中提取第一个成分t1，使t1=E0w1.其中t1为x1，x2，…，xm线性组合，w1为矩阵对应于E'0F0F'0E0矩阵最大特征值的特征向量.

建立因变量Y 关于t1的回归，使得

用残差矩阵E1和F1取代E0和F0，使用同样的方法求第二个成分t2.以此类推，求得剩下的成分t3，t4，…，tA，最终有

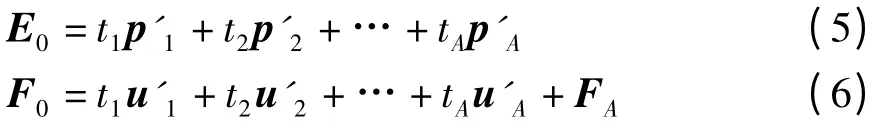
由于t1，t2，…，tA均可以表示成E1，E2，…，Em的线性组合，因此，式(6)可以还原成y*=F0k关于xj*=E0k的回归方程形式，即

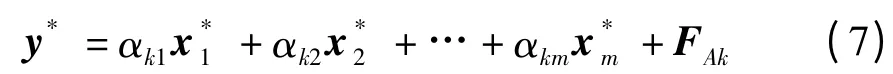
其中，k=1，2，…q，FAk是残差距阵FA的第k 列.

1.6 支持向量机建模

支持向量机可对线性或非线性问题进行回归.对于线性问题，SVM 采用线性回归函数［12］f( )x=wx + b(w 为估计权值向量，b 为偏置)拟合数据{xi，y}，i=1，2，…，n，xiRn，yR.若训练数据在ε精度下无误差地用线性函数拟合，即

此时，优化目标为

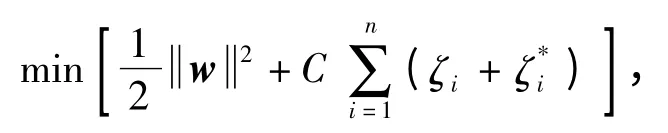
其中，C 为错误的损失函数，C＞0.对原问题使用拉格朗日乘数法求解后，其对偶问题为

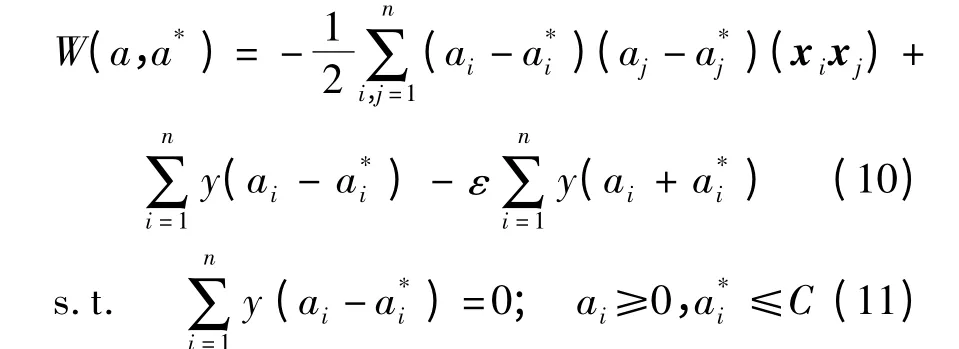
其中ai为进行拉格朗日乘数法运算时引入的乘子.

由最大化函数可知支持向量单因变量线性回归函数为

其中，ai和只有小部分不为0，其对应的样本为支持向量.

对于非线性问题，SVM 使用非线性转换将原问题映射到更高维空间中的线性问题进行求解.在高维特征空间中，将核函数K ( xi，xj)替换为线性问题的内积运算.此时，式(10)、(11)、(12)变为:

由最大化函数可知支持向量单因变量线性回归函数为

2 实验结果与讨论

2.1 PLS 模型成分的提取

从工厂获得的240 组数据随机分为180 组训练集和60 组测试集.为确定成分个数A，使用交叉有效性法则.

式中:yi为实际值;A(-i)为样本点i 在使用除样本i后剩余样本提取A 个成分建立的回归方程的拟合值(A-1)i为样本点i 在使用所有样本提取A -1 个成分建立的回归方程的拟合值.

交叉有效性测量成分th对单因变量偏最小二乘法模型精度的边际贡献有如下条件:

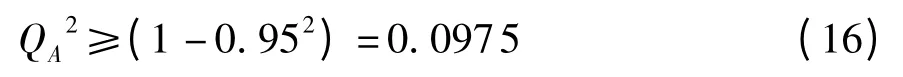
增加成分th，可以明显改善模型.

使用训练集进行建模，根据交叉有效性法则，当提取第3 个成分后QA2 ＜0.097 5，因此文中选择前两个组分t1、t2.

2.2 SVM 核函数的选择

使用SVM 建模时需要确定最佳的核函数［13］.常用SVM 的核函数有:线性核函数、多项式核函数、径向基核函数、Sigmoid 核函数.分别使用不同的核函数测试模型，采用均方根误差(RMSE)［14］来衡量模型预测值和实际值的误差，再引入预测值与测量值的皮尔逊相关常数r［15］来评价预测值与实际值的变化趋势，r 绝对值越接近1，表明预测值与实际值的变化趋势越一致，见式(17)、(18):

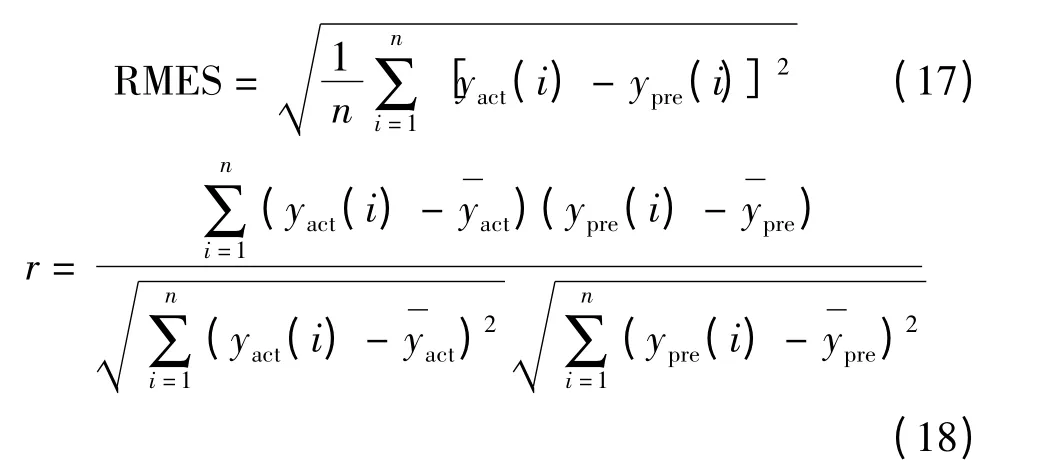
式中，yact、act分别为抗张强度实际值和实际值的平均值分别为抗张强度预测值和预测值的平均值.

选用不同的核函数分别对训练集通过SVM 建模，用模型对测试集进行预测，得到的数据见表2.

表2 SVM 不同核函数预测精度对比Table 2 SVM predicting accuracy comparison among different kernel type

由表2 可知，使用线性核函数的模型预测值与实际值的相关系数最高，且均方根误差最低，因此使用线性核函数进行建模效果最佳.

2.3 PLS 与SVM 精度对比

用训练集建立偏最小二乘回归与支持向量机模型后，使用测试集进行验证.采用均方根误差、皮尔逊相关系数进行精度分析.

经Matlab 偏最小二乘预测与支持向量机预测，可得其RMSE 分别为338 和307 N/m，皮尔逊相关系数分别为0.909 和0.918，由此可知，SVM 模型的均方根误差与最大相对误差更小，相关系数更大.由图1可以看出，训练集中，使用PLS 和SVM 模型的预测值与45°线接近程度较好，其中PLS 模型的预测值较SVM 模型的预测值而言更加分散.因此，SVM 模型的预测精度要高于PLS 模型.

2.4 模型的简化

在实际生产中，一些依据机理分析选取的操作参数由于生产设备可调控性限制与抗张强度的相关系数很低.这些参数对模型预测值的结果影响小并且可能对模型精度存在一定的干扰，此外，大量的模型参数会延长程序计算获得预测值的时间.因此，文中将使用筛选相关系数的方法对模型参数进行删减，以考察简化模型的应用性.

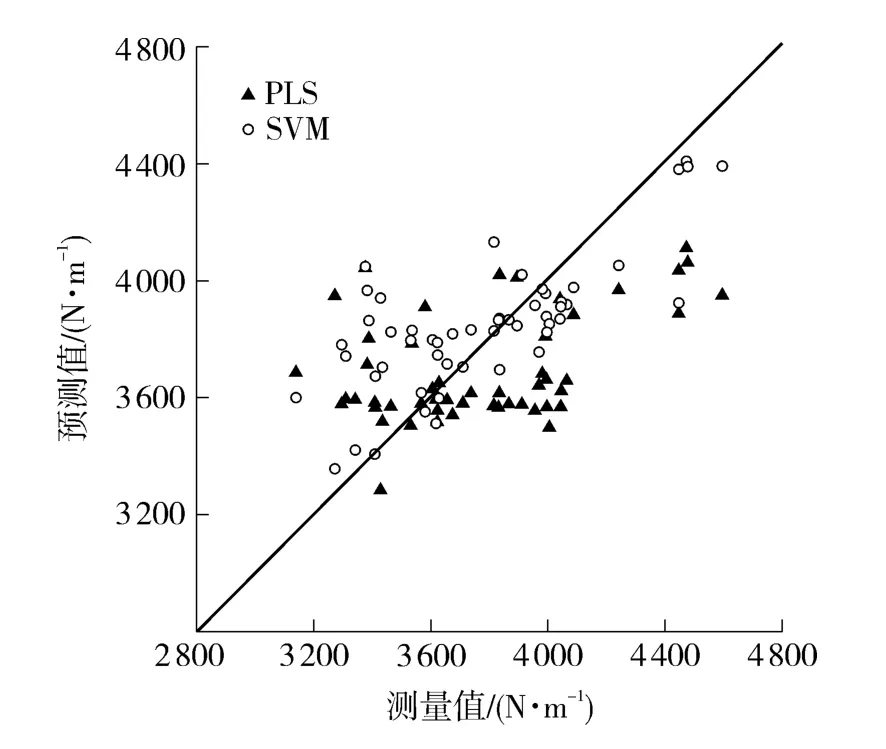
图1 SVM 模型与PLS 模型抗张强度的预测Fig.1 Tensile strength prediction based on SVM model and PLS model

使用Matlab 计算出所有模型参数与抗张强度的相关系数后，将其中与抗张强度弱相关［16］0.300)的参数剔除后得到的操作参数见表3，根据这些参数建立PLS 和SVM 简化模型，其对应所得的RMSE 分别为348 和321 N/m，皮尔逊相关系数分别为0.899 和0.909;预测值和测量值的对比如图2 所示.

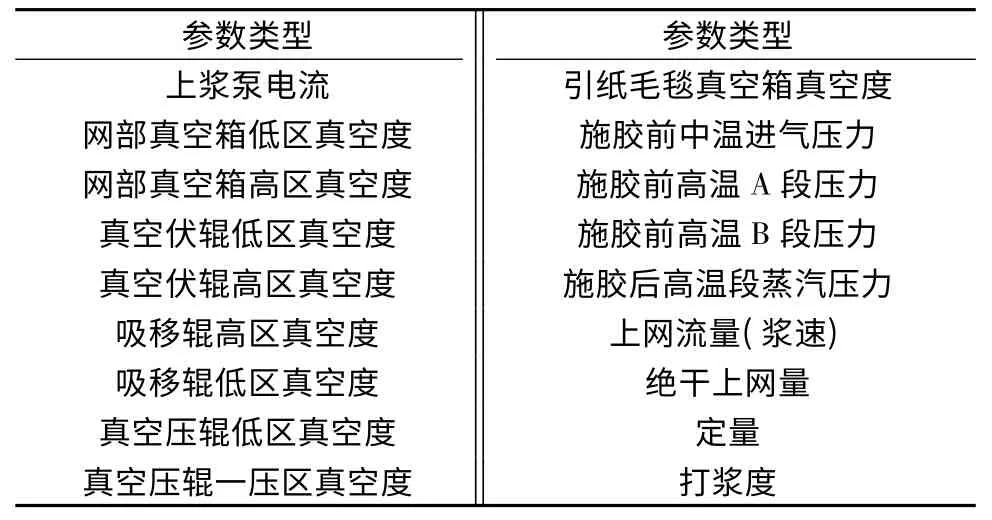
表3 简化后的模型参数Table 3 Reduced model parameters

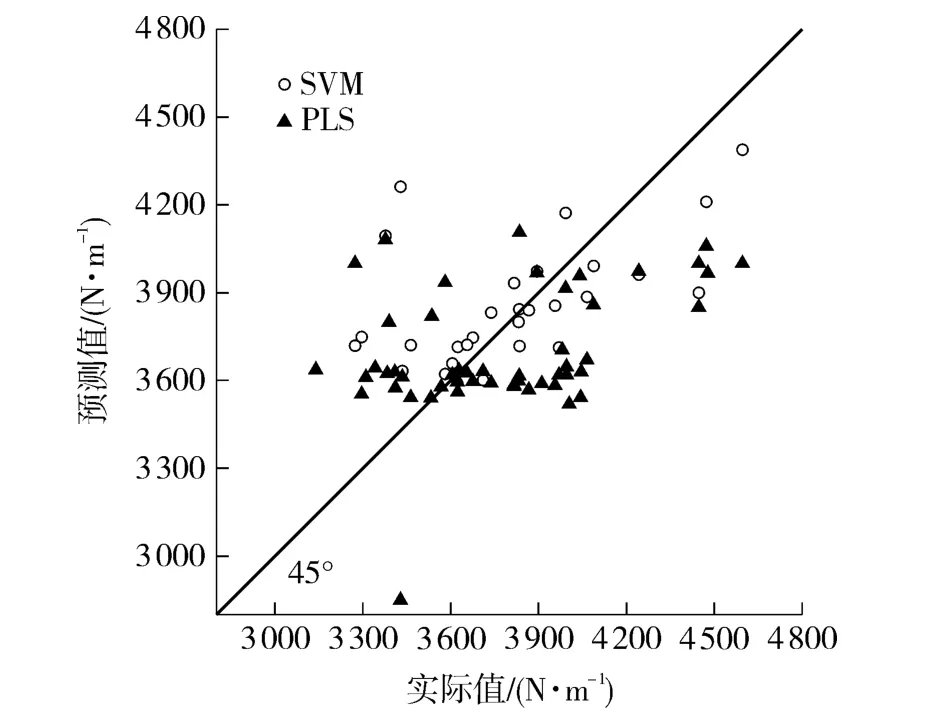
图2 SVM 简化模型与PLS 简化模型抗张强度的预测Fig.2 Tensile strength prediction based on simplified SVM model and simplified PLS model

综合上述分析可知，简化后的PLS 和SVM 模型RMSE 值较简化前分别下降了10 和14 N/m，两个模型的RMSE 降低幅度均在5%之内;两个简化模型的相关系数下降也均在0.01 以内.

2.5 纸张抗张强度最优模型

使用模型对生产现场进行指导时，往往有大量的数据需要处理.分别使用60 组数据通过SVM 模型以及简化SVM 模型进行预测，耗时分别为2.183和2.060 s.由此可知，简化后的SVM 模型平均耗时比原SVM 模型缩短了约5%，同时简化后模型精度变化不大，原SVM 模型精度为0.918，简化后的SVM模型为0.909，但简化模型参数由30 个减至18 个，减少了40%的参数对生产的指导效果较原模型而言有了较大的提升.综上所述，简化的SVM 模型更适用于现场预测.

3 结语

(1)偏最小二乘法和支持向量机模型的测试值与预测值的皮尔逊相关系数均达到0.9，表明这些模型均可以对纸张抗张强度建模.偏最小二乘法模型简化前后的RMSE 分别为338、348 N/m;支持向量机模型简化前后的RMSE 则分别为307、321 N/m.比较而言，SVM 简化模型更适合该厂纸张抗张强度的预测.

(2)模型简化后参数减少40%，简化的支持向量机模型预测用时最短，为2.060 s.由于所选取的因素均可在生产现场获取和调节，与现有的基于Page 原理、Shear-lag 原理及神经网络等建立的模型相比，对现场生产的指导性更高.在现场需要处理大量数据，简化的支持向量机模型预测速度最快，且精度较高，因此更适用于现场预测.

抗张强度的支持向量机法预测为有效控制产品质量提供了理论基础.使用支持向量机法在线预测抗张强度，可以降低以往调节方式的滞后性，从而达到在线控制的目的.但由于不同造纸厂的设备型号以及生产纸种、规格不同，文中所获得的模型的应用具有一定的针对性.为获得应用性更广且具有较高精度的纸张抗张强度模型，可尝试从不同纸厂获取样本进行建模.同时模型误差有待改良，造成模型误差的原因有:采集的样本数较少，采集数据存在时间差等.而且文中使用统计分析方法，对选取数据依赖性较强，对此问题的解决有待进一步研究.

［1］Scott W.Potential application of predictive tensile strength models in paper manufacture(Part Ⅱ):integration of a tensile strength model with a dynamic paper machine material balance simulation［C］∥TAPPI Papermakers Conference Proceedings.Atlanta:GA TAPPI Press，2001.

［2］Page D H.A theory for the tensile strength of paper［J］.TAPPI Journal，1969，52(4):674-679.

［3］Anson S J I'，Karademir A，Sampson W W.Specific contact area and the tensile strength of paper ［J］.Appita Journal，2006，59(4):297.

［4］陶劲松，刘焕彬，陈小泉，等.纸页水分含量对纤维相对结合面积和剪切抗张强度的影响［J］.造纸科学与技术，2007，26(2):1-5.Tao Jin-song，Liu Huan-bin，Chen Xiao-quan，et al.Effect of sheet moisture content on fiber relative bonded area and shear tensile strength［J］.Paper Science ＆ Technology，2007，26(2):1-5.

［5］De Ruyo A，Fellers C.Paper structure and properties［J］.Marcel Dekker，1986，24(6):67.

［6］Axelsson A.Fibre based models for predicting tensile strength of paper［D］.Finland:Luleå University of Technology，2009.

［7］王宝玉.木浆纤维表面化学特性与纸页强度关系的研究［D］.广州:华南理工大学轻工与食品学院，2011.

［8］Navita，Kumar Ra.Articficial neural network modeling for tensile strength of paper in paper manufacturing process international［J］.Information Technology and Knowledge Management，2011，4(2):409-412.

［9］Wold S，Ruhe A，Wold H，et al.The collinearity problem in linear regression.the partial least squares(PLS)approach to generalized inverses［J］.SIAM Journal on Scientific and Statistical Computing，1984，5(3):735-743.

［10］Vapnik V.The nature of statistical learning theory［M］.New York:Springer，2000.

［11］王惠文.偏最小二乘回归方法原理及其应用［M］.北京:国防工业出版社，2000:123-202.

［12］Smola A J，Schölkopf B.A tutorial on support vector regression［J］.Statistics and Computing，2004，14(3):199-222.

［13］王睿.关于支持向量机参数选择方法分析［J］.重庆师范大学学报:自然科学版，2007，24(2):36-38.Wang Rui.Method analyze about support vector machine's parameter［J］.Journal of Chongqing Normal University:Natural Science Edition，2007，24(2):36-38.

［14］Chai T，Draxler R R.Root mean square error(RMSE)or mean absolute error(MAE)?［J］.Geoscientific Model Development Discussions，2014，7(1):1525-1534.

［15］Adler J，Parmryd.Quantifying colocalization by correlation:the Pearson correlation coefficient is superior to the Mander's overlap coefficient［J］.Cytometry Part A，2010，77(8):733-742.

［16］Buda A，Jarynowski A.Life time of correlations and its applications［M］.Poland:Andrzej Buda Wydawnictwo NiezaleL'L'ne，2010.