基于时空特性的短时交通流预测模型*

邱敦国 兰时勇 杨红雨

(四川大学 计算机学院，四川 成都 610065)

随着汽车大量增加，城市交通拥堵问题日趋严重.为了缓解城市道路的交通拥堵现象，采用有效的方法对城市路网的交通流量进行合理分配变得非常重要，其中，对道路实施交通流控制与诱导是控制交通流合理分配的一个关键问题，其核心之一是实时、准确地进行短时交通流预测.

各国学者对短时交通流预测进行了长期深入的研究，提出了近百种预测方法.目前，大体可将这些预测方法分为两类:第1 类是以数理统计和微积分等传统数学和物理方法为基础的预测方法，包括时间序列预测［1］、历史均值预测［2］、卡尔曼滤波模型预测［3］等;第2 类是以现代科学技术和方法为主要研究基础而形成的预测模型，包括支持向量机［4］、神经网络［5］、混沌理论［6］等.第1 类预测方法的特点是对研究对象追求严格意义上的数学推导和明确的物理意义，而第2 类预测方法更重视对真实交通流现象的拟合效果.

由于交通流是一个具有一定规律的历史周期变化系统，每天不同时间段的交通流具有特定规律性，并以一天为单位进行周期变化，因而具有历史周期性;同时交通流又是受上下游交通流影响的空间相关性系统，当上游或下游交通流发生变化时，又会对当前时刻下一时段交通流形成影响，即各点的交通流不是独立的系统，而是相互关联、相互影响的系统，因而具有空间相关性.用第1 类方法对交通流进行预测时，根据道路的现有流量与历史交通流特征可以得到很好的预测效果，但是不能对上下游交通流的影响进行预测.当道路出现车祸、修路、交通管制等偶发因素时，预测的准确性降低.在第1 类预测方法方面，Lee 等［7］采用差分自回归移动平均模型(ARIMA)预测交通流，Williams 等［8］在ARIMA 模型的基础上考虑了交通流的周期性，采用季节性差分自回归移动平均模型(SARIMA)预测交通流，邱敦国等［9］针对交通流的双周期特性，在SARIMA 模型基础上，提出采用双周期季节性差分自回归移动平均模型(DSARIMA)预测交通流，在交通流偶发因素影响不是太大的情况下，均有不错的预测效果.第2类预测更多地根据现有交通状态及交通流上下游的关系等进行预测，对道路出现偶发因素引起的交通流波动有更好的预测效果，但对交通流的历史周期性考虑较少，总体预测结果波动较大.就第2 类预测方法来说，田晶、刘汉丽等［10-11］采用的前向(BP)神经网络预测方法和马君、林鑫、郭磷等［12-14］采用的径向基函数(RBF)神经网络预测方法，对短时交通流的预测都取得了不错的效果.国内外有部分学者尝试采用有效的方法将交通流的历史特性与空间相关性相结合，以兼顾二者的优势.常刚等［15］提出一种基于时空依赖性的区域路网短时交通流预测模型，将时空自回归差分移动平均模型(STARIMA)引入到城市区域路网的交通流预测之中，在时间序列模型基础上引入空间属性，通过一个空间权重矩阵来体现多路段交通流之间的空间拓扑关系;该模型在采用时间序列进行交通流预测时，同时考虑了交通流的空间属性，相比考虑交通流单一特性的模型，预测效果更好;但是，STARIMA 模型是在ARIMA 基础上引入空间特性，只是考虑了交通流序列的历史特性，没有考虑交通流序列的周期特性，因此，不能更真实地表达交通流的历史周期特性与空间相关特性，影响了其预测结果的准确性.

文中根据交通流的时空特性，提出一种既结合交通流的历史周期性，又结合交通流空间相关性的预测模型——SARIMA-RBF 模型，该模型融合了SARIMA模型在交通流历史周期性预测上的优势和RBF 神经网络模型在交通流空间相关性预测上的优势.

1 模型介绍

1.1 SARIMA-RBF 预测模型

SARIMA-RBF 预测模型综合了SARIMA 时间序列预测模型和RBF 神经网络模型，该模型首先采用SARIMA 模型预测下一时段的预测值，并将该预测值作为RBF 神经网络模型的一个输入值，同时将与该时间序列相关联的其他测试值作为RBF 神经网络的输入值，采用RBF 神经网络模型得出输出值，并将该输出值作为SARIMA-RBF 模型对下一时刻的预测值，该模型的结构如图1 所示，模型的输入层总数为M+1(M 为空间相关性影响因素总数)，隐含层结点数为N，输出层结点数为1，x1，x2，…，xM为其他影响因子.

图1 所示的SARIMA-RBF 模型的输出为

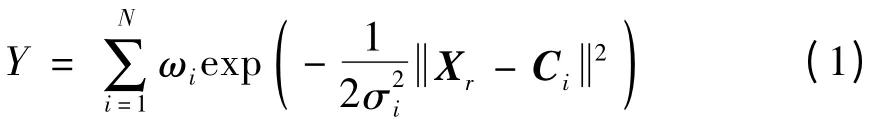
式中:Xr=，为第r 个输入样本;r=1，2，…，R，R 表示输入样本总数;Ci为网络第i个隐含层结点的中心;σi为网络第i 个隐含层结点径向基函数的宽度;ωi为隐含层到输出层的连接权值;为欧式范数;xs为SARIMA 预测值，SARIMA 预测模型为

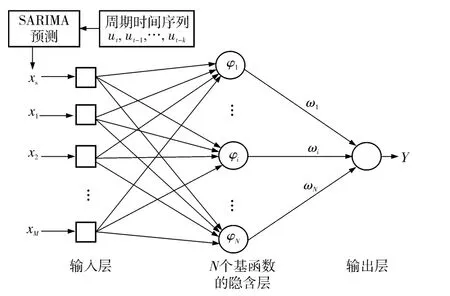
图1 SARIMA-RBF 网络结构Fig.1 SARIMA-RBF network structure

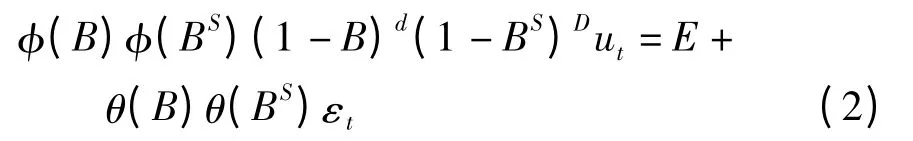
式中:ut为交通流时间序列;d 为差分的次数;S 和D分别为季节周期的长度和季节差分的次数;E 为常数;εt为模型残差项，服从均值为0 且方差为常数的正态分布;B 是后移算子;BS表示季节后移算子.平稳可逆模型的自回归系数多项式为

季节平稳可逆模型的自回归系数多项式为

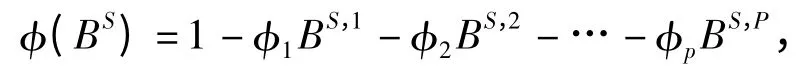
平稳可逆模型的移动平滑系数多项式为

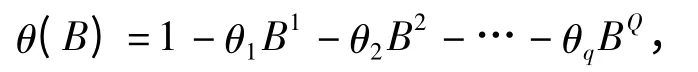
季节平稳可逆模型的移动平滑系数多项式为

式中，P 为模型中自回归模型(SAR)项的滞后阶数，Q 为模型中移动平均模型(SMA)项的滞后阶数.

1.2 SARIMA-RBF 模型求解

SARIMA-RBF 模型求解分两步完成，第1 步是用SARIMA 模型，根据当前点位的历史数据，预测该点下一时刻的预测值xs;第2 步是根据预测值xs，结合该点上下游关联的交通流数据x1，x2，…，xM采用RBF 模型进行预测.

1.2.1 SARIMA 预测算法的实现

SARIMA 模型预测考虑了交通流的周期特性，是一个非常复杂的过程，为了简化周期性计算的复杂性，文中根据交通流的实时特性和周期特性采用如下算法来进行交通流预测.

实时数据预测:采用当前要预测时间段的前L1段时间的交通流用ARIMA 模型来预测，预测结果记为

周期数据预测:采用当前预测时间段的前L2天同一时间段的交通流用ARIMA 模型来预测，预测结果记为

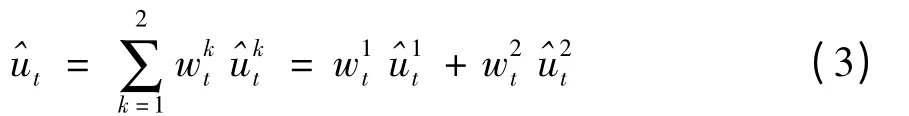
由于交通流是一个以“天”为单位的周期变换时间序列，每天同一时间点，交通流相近，但是也受大的交通趋势的影响，因此，越是离当前时间点近的日期，其同时段交通流相近度更大，所以文中在计算与时，不是按照传统的贝叶斯组合模型对每个数据采用相同的权重，而是对离预测点时间越近的数据设置更大的权重，具体计算如式(6)与(7)所示:

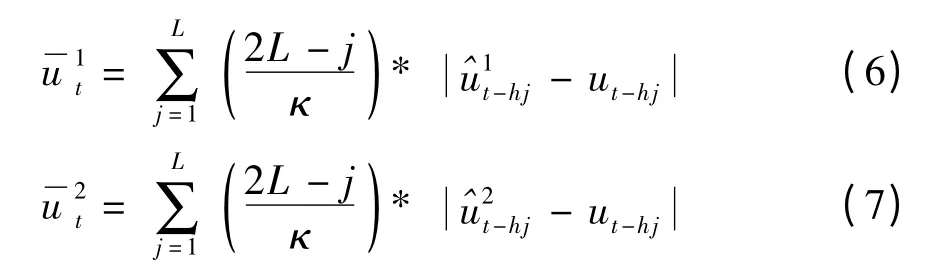
h 为每天所取的时间段数，文中采用5 min 作为交通流时间段，因此，h 的取值为288.ut为交通流实际值.表示当前时刻前L 天同一时段采用实时数据预测值与实际值之差的绝对值累加之和，表示当前时刻前L 天同一时段采用周期数据预测值与实际值之差的绝对值累加之和值越大，表示采用实时数据预测值与实际值差距更大，预测准确率更低，则在下一次的预测中，实时数据预测的权值就越小，值同理.

1.2.2 RBF 预测算法的实现

RBF 神经网络预测首先需要对RBF 网络进行学习，确定RBF 神经网络的隐层结点数N、中心值Ci、基宽度σi及网络隐含层与输出层的权值ωi，确定好以上参数后，即完成RBF 网络学习.

文中RBF 神经网络学习采用混合学习算法，分为两个阶段，具体如下.

(1)确定高斯函数的参数的初值

文中根据输入样本，采用改进的K-means 聚类算法确定数据的隐层结点数N、中心值Ci.

在K-means 聚类算法中，在进行样本分类时，采用欧氏距离作为判定两个样本之间的距离，如样本α=(αs，α1，α2，…，αM)和样本β=(βs，β1，β2，…，βM)的欧氏距离为

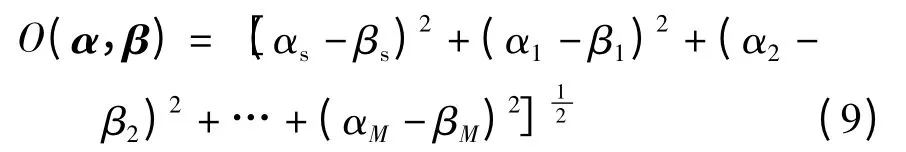
在文中的RBF 样本数据中，SARIMA 模型预测值分量αs相比其他分量α1，α2，…，αM应具有更大的权值，因此，为了突出αs分量的作用，将欧氏距离的计算公式修改为

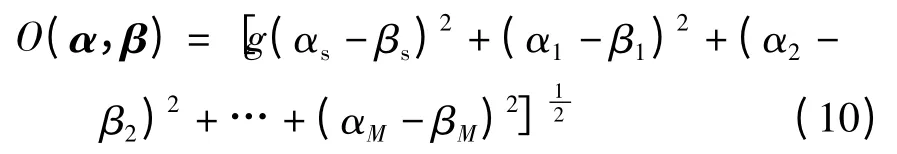
式中，在αs分项计算时，加入权重g(g≥1)，这样可更好地增加αs分项的权重，得到更好的分类效果.

采用改进的K-means 聚类算法确定好隐层节点数与中心值后，计算数据中心之间的最大距离omax，再由求得基宽度σi.

(2)求网络隐含层与输出层的权值

高斯函数的中心和方差确定后，采用有监督的最小二乘法求出网络隐含层与输出层的权值:

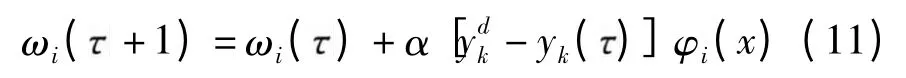
通过以上步骤完成RBF 学习后，即可用学习的RBF 进行预测，预测结果作为SARIMA-RBF 模型最终的交通流预测结果.

2 实验结果与分析

2.1 数据来源

本实验数据取自成都市三环路交通流量检测系统，该路段是全封闭无红绿灯控制的环形道路，交通流采用道路外侧整个断面的流量，车辆逆时针方向行驶，共选取了5 个检测点的检测数据，5 个点的分布如图2 所示，其中检测点FA为要预测交通流的点，并在该点上游6 km 处选择了检测点FB，上游4 km 处选择匝道入口流量检测点FC，在下游6 km处选择检测点FE，下游4km 处选择匝道出口流量检测点FD.由于车辆从检测点FB到检测点FA以及从检测点FA到检测点FE的平均耗时均在5 min 左右，因此所有检测点的交通流采用5min 作为一个时间段，共采集了60 天的交通流数据.

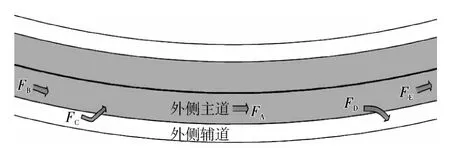
图2 检测点位置图Fig.2 Positions of test points

2.2 模型预测

本次实验分析选择两类情况进行对比，一类是交通流相较往常属于正常情况，一类是相较于往常属于异常情况，并同时采用SARIMA 模型、RBF 模型和SARIMA-RBF 模型进行预测和对比分析.

文中分析了点FA、FB、FC、FD、FE的60 天数据，发现FA点交通流与上下游交通流有极强的关联性.其中FA点下游FD点闸道出口处车流量较大，在早晚高峰期一旦出现车祸等其他现象就会造成拥堵，并同时影响到FA点的交通流量;FA点上游FB点的交通流量也直接影响到FA点下一时刻的交通流量.为预测FA点下一时刻的流量，首先根据FA点的历史流量，用SARIMA 模型预测其下一时刻的流量，然后根据FB、FC、FD、FE点的当前流量，结合作为RBF 模型的输入值，然后进行预测，得到FA点下一时刻的交通流量文中所有预测方法采用Matlab 编程实现，具体预测步骤如下:

(1)采用SARIMA 模型根据FA点的历史数据先预测FA点第30～60 天从8 点到20 点每天144个5 min 时段样本的交通流数据

(2)根据FB、FC、FD、FE点第30～58 天从8 点到20 点的数据，结合步骤(1)预测的点下一时段的交通流预测值作为RBF 的输入，得到FA点下一时段交通流预测结果，并用预测结果与实际结果之差的期望最小来调整RBF 模型的参数，完成对RBF 模型的训练.

(3)按步骤(1)预测出FA点第59 天和第60 天从8 点到20 点的144 个5 min 时段样本的交通流，然后根据FB、FC、FD、FE点第59 天和第60 天从8 点到20 点的数据，采用步骤(2)训练的神经网络模型，预测第59 天和第60 天从8 点到20 点的144 个5 min 时段样本的交通流

2.3 预测结果评价

为考察SARIMA-RBF 模型的准确性，文中采用单一SARIMA 模型和RBF 模型对FA点交通流预测作对比，并选取了3 个不同时段的预测数据作为对比:时段1 是第59 天早上8 点到10 点，共24 个样本;时段2 是第60 天早上8 点到10 点，共24 个样本;时段3 是60 天下午14 点到16 点，共24 个样本.其中，时段1 和2 是早高峰时段，交通流变化比较大，而时段3 是下午平峰时段，交通流比较平稳;时段1 与时段3 的交通流处于正常状态，与往天同时段的交通流变化不大，而时段2 的交通流处于异常状态，交通流与往日同时段的交通流分布有明显差异.

为评价模型预测性能的优劣，文中选用3 种衡量标准作为预测精度的统计量，从不同侧面反映了算法的预测精度.这3 个指标分别为平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方差(MSE):

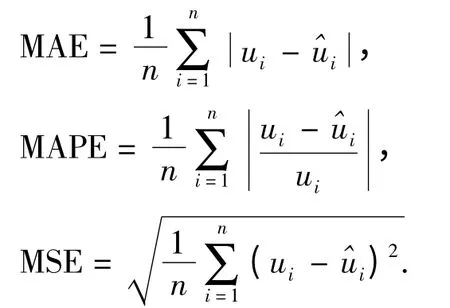
式中:ui为交通流真实值;^u为交通流预测值;n 为预测样本数，文中n 取值为24，通过预测3 个时段24 个样本的数据作为比较衡量标准.表1 示出了时段1、2、3 各24 个样本的预测比较结果.

对比时段1 和时段3 的3 种预测结果可知，RBF模型预测误差最大，SARIMA 模型次之，SARIMA-RBF模型最好，不过，SARIMA-RBF 模型的结果与SARIMA 模型相比变化不大.

由时段2 的预测结果可见，由于该时段交通流与往日同时段交通流出现异常，采用SARIMA 模型预测误差最大，RBF 模型次之，SARIMA-RBF 模型预测结果最好.

从表1 可以看出，SARIMA-RBF 模型预由于同时考虑了交通流的历史周期性和空间相关性，具有更好的预测效果，尤其是在交通流异常时段，预测效果更明显.

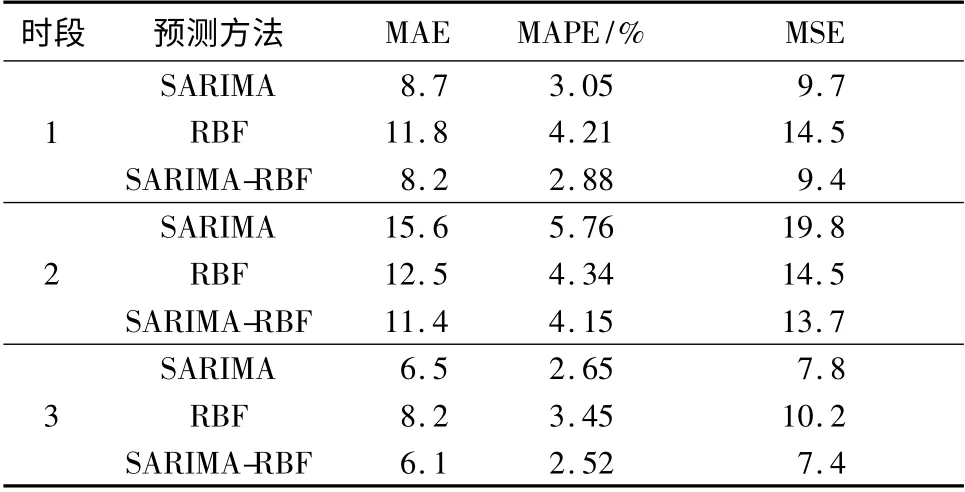
表1 3 个时段3 种模型的预测误差比较Table 1 Comparison among forecast results of three models in three periods of time

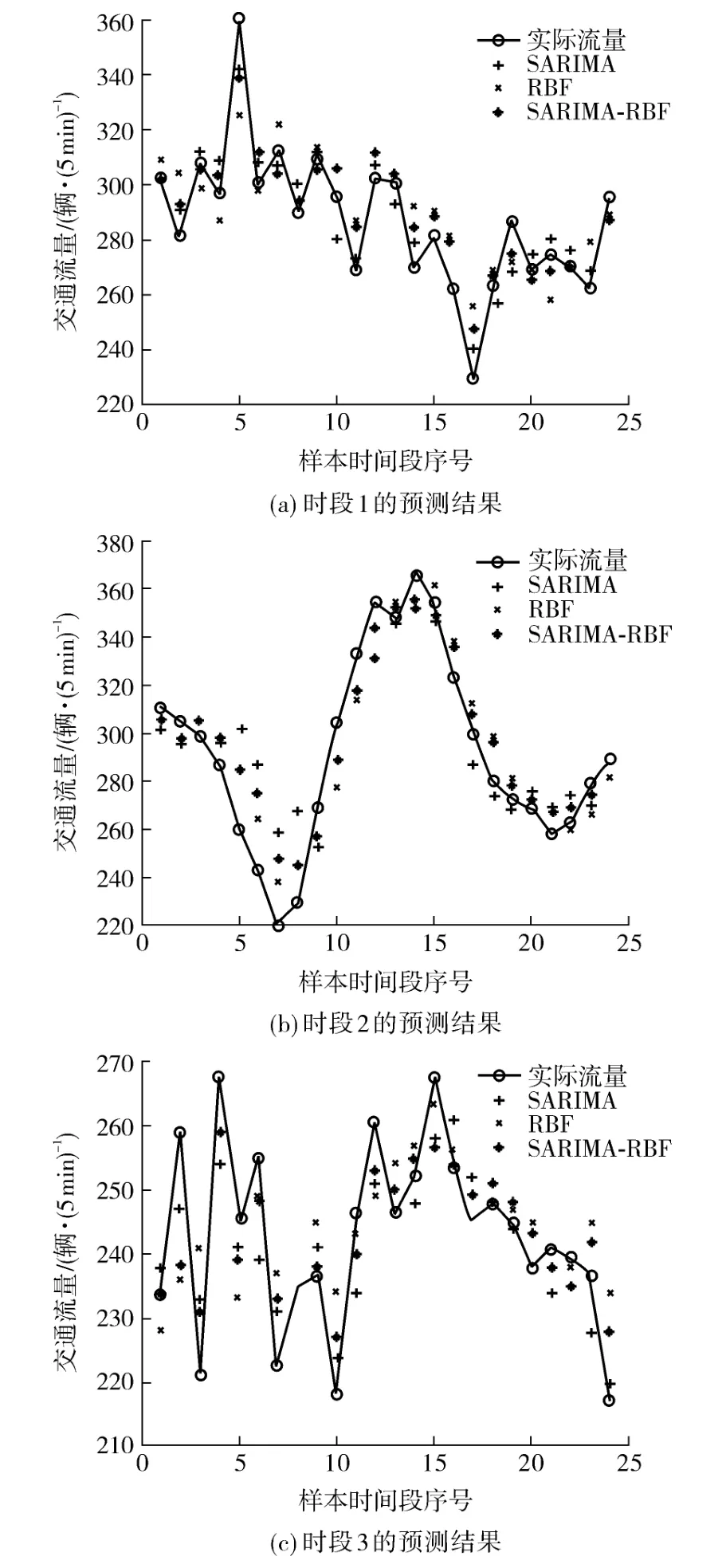
图3 3 种模型预测结果与真实数据对比Fig.3 Comparison of three models-based forecast results with real results

图3 示出了用3 种模型预测的交通流数据与真实交通流数据的对比结果，可以看到，SARIMA-RBF模型相比SARIMA 模型和RBF 模型在3 个预测时段中都有更好的预测效果.

3 结论

文中提出一种结合交通流的历史周期性和空间相关性的预测模型——SARIMA-RBF 预测模型.该模型针对交通流的历史周期性，采用SARIMA 模型进行预测，针对交通流的空间相关性，采用RBF 神经网络模型进行预测，并将SARIMA 模型预测值作为RBF 模型的输入值，采用RBF 神经网络模型得出输出值，并将该输出值作为SARIMA-RBF 模型对下一时刻的预测结果.实验结果证明，该模型相对于仅考虑交通流单一特性的预测模型具有更好的预测效果.由于文中的交通流预测模型仅在成都市三环路交通流预测数据中进行应用，下一步将针对其他更复杂的道路情况进行预测，以进一步改善模型的参数，使预测模型的适应性更好.

［1］Ahmaed M S，Cook A R.Analysis of freeway traffic timeseries data by using Box-Jenkins technique ［J］.Transportation Research Board，1979(722):1-9.

［2］Stephanedes V J，Michalopoulos P G，Plum R A.Improved estimation of traffic flow for real-time control［J］.Transportation Research Record，1981(795):28-39.

［3］Okutani I，Stephanedes Y J.Dynamic prediction of traffic volume through Kalman filtering theory［J］.Transportation Research Part B:Methodological，1984，18(1):1-11.

［4］Castro-Neto M，Jeong Y-S，Jeong M-K，et al.Online-SVR for short-term traffic flow prediction under typical and atypical traffic conditions［J］.Expert Systems with Applications，2009，36:6164-6173.

［5］Vlahogianni E I，Karlaftis M G，Golias J C.Optimized and meta-optimized neural networks for short-term traffic flow prediction:a genetic approach ［J］.Transportation Research Part C:Emerging Technologies，2005，13:211-234.

［6］Xue J N，Shi Z K.Short-time traffic flow prediction based on chaos time series theory［J］.Journal of Transportation Systems Engineering and Information Technology，2008，8(5):68-72.

［7］Lee S，Fambro D B.Application of subset autoregressive integrated moving average model for short-term freeway traffic volume forecasting ［J］.Transportation Research Record，1999，1678:179-188.

［8］Williams B M，ASCE1 M，Hoel L A，et al.Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process:theoretical basis and empirical results［J］.Journal of Transportation Engineering，2003，129(6):664-672.

［9］邱敦国，杨红雨.一种基于双周期时间序列的短时交通流预测算法［J］.四川大学学报:工程科学版，2013，45(5):64-68.Qiu Dun-guo，Yang Hong-yu.A short-term traffic flow forecast algorithm based on double seasonal time series［J］.Journal of Sichuan University:Engineering Science Edition，2013，45(5):64-68.

［10］田晶，杨玉珍，陈阳舟.短时交通流量两种预测方法的研究［J］.公路交通科技，2006，23(4):103-106.Tian Jing，Yang Yu-zhen，Chen Yang-zhou.Study on short-term traffic flow forecasting based on two different methods［J］.Journal of Highway and Transportation Research and Development，2006，23(4):103-106.

［11］刘汉丽，周成虎，朱阿兴，等.多子群遗传神经网络模型用于路口短时交通流量预测［J］.测绘学报，2009，38(4):363-368.Liu Han-li，Zhou Cheng-hu，Zhu A-xing，et al.Multipopulation genetic neural network model for short-term traffic flow prediction at intersections［J］.Acta Geodaeticaet Cartographica Sinica，2009，38(4):363-368.

［12］马君，刘小冬，孟颖.基于神经网络的城市交通流预测研究［J］.电子学报，2009，37(5):1092-1094.Ma Jun，Liu Xiao-dong，Meng Ying.Research of urban traffic flow forecasting based on neural network［J］.Acta Electronica Sinica，2009，37(5):1092-1094.

［13］林鑫，王晓晔，王卓，等.基于蚁群聚类算法的RBF 神经网络交通流预测［J］.河北工业大学学报，2010，39(3):42-45.Liu Xin，Wang Xiao-ye，Wang Zhuo，et al.Traffic flow forecasting based on ant colony clustering algorithm and RBF neural network［J］.Journal of Hebei University of Technology，2010，39(3):42-45.

［14］郭磷，方廷健，叶加圣.基于GGA 的RBF 神经网络及其在交通信息预测中的应用［J］.模式识别与人工智能，2006，19(6):831-835.Guo Lin，Fang Ting-jian，Ye Jia-sheng.Genetic gradient algorithm based RBF neural network and its applications to traffic information predietion［J］.Pattern Recognition and Artificial Intelligence，2006，19(6):831-835.

［15］常刚，张毅，姚丹亚.基于时空依赖性的区域路网短时交通流预测模型［J］.清华大学学报:自然科学版，2013，53(2):215-221.Chang Gang，Zhang Yi，Yao Dan-ya.Short-term traffic flow forecasting model for regional road network based on spatial-temporal dependency ［J］.Journal of Tsinghua University:Science and Technology，2013，53(2):215-221.