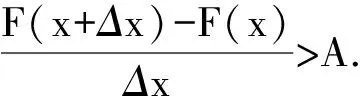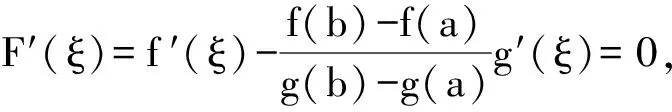柯西中值定理的新证明*

蒋叶聪， 张晓青， 江蓉华

(重庆师范大学 数学学院，重庆 401331)

1 预备知识

柯西中值定理是拉格朗日中值定理的推广，是数学分析中十分重要的内容，也是微分学的基本定理之一. 关于柯西中值定理的证明，一般是构造辅助函数，再利用罗尔定理得出结果[1]，也有学者利用其它方法来证明定理. 宋铁莎运用连续函数的介值定理、单调有界定理给出了柯西中值定理的一个证明[2].张玉忠应用连续函数的性质和闭区间套定理给出了柯西中值定理的又一证法[3].黄德丽用5种不同的方法证明了柯西中值定理[4]. 这些证明方法拓宽了柯西中值定理的证明思路，同时，探索如何利用新的方法证明柯西中值定理也十分有意义.

近年来，许多学者探索出了新的利用完备性定理的方法来证明柯西中值定理. 2005年，张彩霞对区间套定理给出一个推论，然后建立了4个引理并在此基础上通过构造区间套依次证明了罗尔中值定理、拉格朗日中值定理和柯西中值定理[5]. 2012年，张琳和郭三刚通过反证法给出了罗尔定理和拉格朗日中值定理的证明并利用拉格朗日中值定理证明了柯西中值定理[6]. 通过完备性定理证明柯西中值定理的方法有很多，但至今没有通过有限覆盖定理证明柯西中值定理的方法. 1991年，曲立学利用有限覆盖定理证明了拉格朗日中值定理[7]，基于文献[7]的思想，利用有限覆盖定理和达布定理[8]，通过构造新的辅助函数，并利用反证法，结合连续函数的性质，给出了柯西中值定理一种新的证明方法.

引理1[8]达布定理(导函数的介值定理) 设y=f(x)在(A，B)区间中可导，又设[a，b]包含于(A，B)，且f ′(a)

引理2[1](有限覆盖定理) 若开区间所成的区间集E覆盖一个闭区间[a，b]，则总可以从E中选出有限个开区间，使这有限个开区间覆盖[a，b].

2 定理的证明

柯西中值定理：若f(x)与g(x)在闭区间[a，b]上连续，在开区间(a，b)内可导，并且g′(x)≠0，则在(a，b)内至少存在一点ξ，使得

证明因为对任意x∈[a，b]，g(x′)≠0，故g(a)≠g(b).

下面证明存在x∈(a，b)，使得F′(x)=A.

若对任意的x∈(a，b)，F′(x)≠A，则有3种情况之一成立：(1) F′(x)>A；(2) F′(x)

由引理1可得：若 (3) 成立，则存在x0∈(x′，x″)⊂(a，b)，使得F′(x0)=A，矛盾.可知 (3) 不成立.

从而F(x1)-F(d)>A(x1-d)；F(y1)-F(x1)>A(y1-x1)；F(x2)-F(y1)>A(x2-y1)；…；F(b-ε)-F(xn)>A(b-ε-xn).等式左右两端相加可得F(b-ε)-F(d)>A(b-ε-d). 因为F(x)在b点连续，所以F(b)-F(d)≥A(b-d)，同理可得F(d)-F(c)>A(d-c)；F(c)-F(a)≥A(c-a)；故：F(b)-F(a)>A(b-a)=F(b)-F(a)，矛盾.

同理可证，若F′(x)

参考文献：

[1] 欧阳光中，朱学炎，金福临，等. 数学分析[M].北京：高等教育出版社，1987

[2] 宋铁莎. 柯西中值定理的一个证明[J]. 广西师范大学学报：自然科学版，1994，12(2)：30-32

[3] 张玉忠. Cauchy中值定理的又一证法[J]. 重庆工商大学学报：自然科学版，1994，11(3)：11-13

[4] 黄德丽. 用五种方法证明柯西中值定理[J]. 湖州师范学院学报，2003，25：27-31

[5] 张彩霞. 区间套定理在证明中值定理中的应用[J]. 哈尔滨商业大学学报：自然科学版，2005，21(6)：794-796

[6] 张琳，郭三刚. 微分中值定理及微分 Darboux 定理新证明方法[J]. 陕西理工学院学报：自然科学版，2012，28(2)：67-71

[7] 曲立学. 覆盖定理的若干简单应用[J]. 齐齐哈尔师范学报：自然科学版，1991，11(3)：1-4

[8] 刘三阳，于力，李广明. 数学分析选讲[M]. 北京：科学出版社，2007