紧李群上的卷积

李 智 龙

(四川大学 数学学院，成都 610064)

1 Harr测度[1]

设G是一个紧李群，C(G ；C) 表示G上所有复值连续函数(配备 ∞ 范数)，则存在唯一的 G×G 等变泛函 I ：C(G ；C) →C 满足 I |C=idC且 I 连续.

注1 以下为了方便，用C(G) 代替C(G；C).

引理1[2]L∞(G) ⊂ L2(G) ⊂ L1(G)，其中 Lp(G) 表示相对于G上的Harr测度 p 次Lebesgue可积函数空间(1≤p≤∞)，而且这些嵌入都是连续的.

2 紧李群上的卷积算子

定义1[2]设G是一个紧李群，φ∈C(G)，f∈L1(G)，则卷积φ*f 按如下方式定义

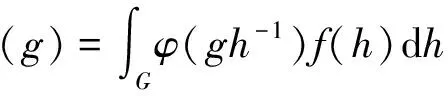
引理2[2]记Tφf=φ*f，则 Tφ是 L1(G) 上的有界算子，并且

‖Tφf‖∞≤‖φ‖∞‖f‖1

于是由引理 1，Tφ诱导了 L2(G) 上的一个有界算子.

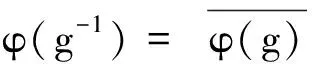
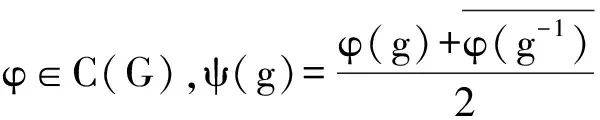
引理4[3]设 H 是一个可分Hilbert空间，A 是 H 上的紧自伴算子，则 H 可分解成A 的特征子空间的直和.

注3 Lp(G)是可分的 (1≤p<∞)，特别地，L2(G) 是可分Hilbert空间.

3 分解定理及例子

由上面的准备，立即得到下面的分解定理.

定理1 设G是一个紧李群，φ 是一个G上的复值连续函数，则

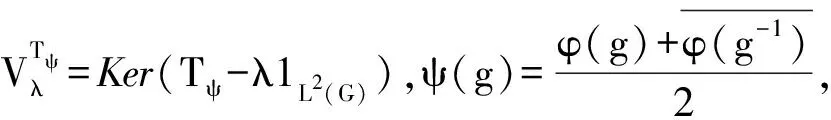
注4Peter-Weyl定理用矩阵函数给出了 L2(G) 的另一种分解方式，参见文献[2].

例1 取φ=ψ=1，则定理 1 给出的分解式为

⊕

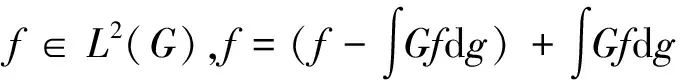
例2 设G = S1，则dθ/2π是G的Harr测度，令

⊕

这也是Peter-Weyl定理给出的分解.

参考文献：

[1] HSIANG W Y. Lectures on Lie Groups，Series on University Mathematics[M]. Singapore：World Scientific，2000

[2] BUMP D. Lie Groups [M]. USA：Springer-Verlag，2004

[3] BREZIS H. Functional Analysis，Soblev Spaces and Partial Differential Equations [M]. USA：Springer，2011