汽车防抱制动系统的分数阶PID控制算法研究*

钱兆刚， 田 丽， 周红艳， 王 勇

(安徽工程大学 电气工程学院，安徽 芜湖 241000)

在汽车行驶中需要制动，特别是紧急制动时，车轮突然抱死会发生汽车方向失控、侧滑、甩尾等危险情况，很容易发生交通事故。汽车防抱死制动系统(ABS)是一种主动安全技术，在制动时自动控制，防止车轮抱死，提高了车辆的制动安全性[1]。目前，ABS的控制策略主要有逻辑门限值控制、最优控制、模糊控制和滑模变结构控制等[2]。逻辑门限值控制没有充分的理论基础，需要大量的实车试验来设定阈值，工作量大。最优控制是控制理论学科上的一种控制方法，需要建立比较精确的数学模型，不然得到的控制效果很差。模糊控制是一种基于知识和经验的控制方法，一般情况下很难建立一个完善的控制规则。在此针对单轮制动模型采用分数阶PID控制，具有较强的控制稳定性和抗干扰能力。最后，设计分数阶PID控制器，嵌入到单轮模型的防抱死制动系统Matlab/Simulink框图中，给出了仿真结果。

1 ABS工作原理及模型建立

实际的汽车防抱死制动系统主要由3部分组成，即车轮轮速传感器、电子控制单元、制动压力调节器，如图1所示。汽车在行驶过程中制动时，制动压力调节器通过增压、保压、减压的调节，控制制动力的大小，防止车轮抱死，汽车的稳定性，转向操纵能力都得到改善，同时制动距离变短，轮胎的使用寿命变长。汽车制动时是利用地面与轮胎之间的摩擦力来减速的，而与摩擦力密切相关的附着系数又与滑移率存在如图2所示的关系。制动时轮速降低，从而就在车身速度与车轮速度之间产生一个差值，这样的现象称为滑移现象[1]。通常用滑移率来衡量制动时车轮的滑移程度，滑移率是指车轮的滑移速度(车轮的实际速度与周向速度之差)与实际速度之比，即

(1)

因此，防抱死制动系统的基本原理就是轮速传感器先采集车轮的速度，电子控制单元也就是ECU根据车轮速度估算出车速，在此基础上进行滑移率的计算，再通过对滑移率值的判断，给制动压力调节器发出调节指令，使得滑移率保持在所期望的值附近。在了解ABS的工作原理后，需对汽车的单轮模型、轮胎、制动系统和控制器进行仿真模型的建立。

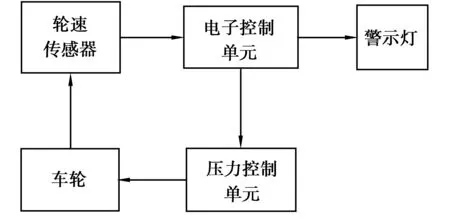
图1 典型ABS模块图

图2 滑移率-附着系数关系曲线

1.1 单轮车辆模型

本文采用简化的单轮模型[1，3]，受力分析如图3所示。

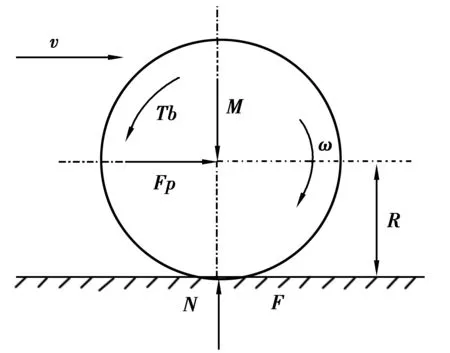
图3 单轮车辆受力分析

根据以上受力图分析可得：

车辆运动方程

(2)

车轮运动方程

(3)

车轮纵向摩擦力

F=μN

(4)

式(2)、式(3)、式(4)中：M为四分之一车体质量(kg)；v为车辆速度(m/s)；F为车轮摩擦力(N)；R不车轮转动惯量(kg·m2)；I为车轮滚动半径(m)；ω为车轮角速度，(rad/s)；μ为车轮与地面间附着系数；N为地面对车轮的作用力(N)。

1.2 轮胎模型

双线性轮胎模型计算公式为[1，4]

(5)

式(5)中：ST为最佳滑移率；S为车轮滑移率；μg为滑移率为100%时的附着系数；μh为峰值附着系数；μ为附着系数。

1.3 制动系统模型

(6)

为方便控制算法的实现，将制动器理解为理想原件。所以，制动器方程可表示为

Tb=kp·P

(7)

式(7)中：kp为制动器制动因数(N·m/kPa)；P为制动液压力(kPa)。

2 控制器设计

2.1 控制算法的选择

传统PID控制器大量应用于工业生产活动中的重要原因就是它的结构简单，容易实现，面对复杂的现场环境具有很强的鲁棒性。实际运行结果表明：众多工业对象在PID控制器控制下，现场的控制效果很好[4]。

分数阶微积分理论已经经过三百多年的发展，但鉴于早期各种条件的限制，其只局限于理论研究。随着计算机科学技术的发展，在材料的记忆、力学和电特性的描述、粘弹性阻尼、分形理论等一系列领域中，相继出现了分数阶微积分[5]。在控制工程中的应用也逐渐盛行起来，分数阶控制理论是对传统的整数阶控制理论的一种概括和补充。分数阶微积分放大了传统整数阶微积分的应用范围在于它的微分、积分的阶次是任意的实数，不是传统的整数。一般分数阶系统就由分数阶微分方程描述：

anDany(t)+…+a1Da1y(t)+a0Da0y(t)=bmDβmu(t)+…+b1Dβ1u(t)+b0Dβ0u(t)

(8)

其中：an>an-1>…>a1>a0≥0，βm>βm-1>…>β1>β0≥0为任意实数；ai(i=0，1，2，…，n)和bj(j=0，1，2，…，m)为任意常数。将设计的分数阶PID控制器就是分数阶微积分的理论与所熟知的PID控制器相结合的产物。

2.2 分数阶PID控制器

分数阶PIλDμ控制器的传递函数为

(9)

式(9)中：λ，μ分别表示积分阶次和微分阶次，λ，μ≥0；KP为比例增益；KI为积分系数；KD为微分系数；U(s)为控制器的输出；E(s)为控制器的误差输入[7]。分数阶PIλDμ控制器能够更灵活地控制受控对象的原因在于它比常规的PID又多了两个可整定的数值——积分阶次λ和微分阶次μ。在合理调节5个参数(KP，KI，λ，KD和μ)的情况下设计出的分数阶PIλDμ控制器，不管对于传统的整数阶系统还是目前的分数阶系统，均能取得优于传统PID控制器的控制效果。其实，所熟知的常规PID控制器就是分数阶PIλDμ控制器在λ=1和μ=1时的情况；并且当λ=1，μ=0时，就是控制器；当λ=0，μ=1时，就是PD控制器。

因为分数阶PID控制器的阶次是分数的，所以采用滤波算法中的Oustaloup算法，在Matlab/Simulink中框图化实现分数阶微积分运算。仿真中的分数阶微积分模块由一个Oustaloup滤波器和一个低通滤波器串联起来[5]，如图4所示。为方便在模型中研究各类控制器，选中Simulink中分数阶PID控制器的所有部分，右键点击CreateSubsystem，建立控制器的子模块。

图4 分数阶PID控制器

3 仿真及结果分析

3.1 仿真模型的建立

经过上面对汽车ABS系统各子模块模型的研究，将其组合在一起，在Matlab/Simulink中搭建单轮模型，所得结构框图见图5。

图5 单轮仿真模型

3.2 仿真结果分析

本文分别对汽车没有ABS，有ABS时采用的模糊控制器以及分数阶PID控制器3种情况进行Matlab/Simulink仿真，得到的各类曲线如图6、图7、图8所示。由图6可知，汽车在制动时，如果没有配备ABS系统，那么滑移率在很短的制动时间内就上升到1，也就意味着车轮快速抱死，这是非常危险的。同样从制动距离曲线看出，汽车从制动到完全停止，经过了很长一段距离，在前方有障碍物等情况下紧急制动时，交通事故的发生率将大大上升。而在汽车配备ABS系统情况下，各项指标将得到了很好地优化。图7和图8分别给出了汽车带ABS系统时，基于模糊控制器和分数阶PID控制器的滑移率和制动距离变化曲线。在这两种控制情况下，结果曲线显示，制动时汽车车轮不会抱死。但模糊控制时，滑移率始终在0.2上下波动，不能稳定在0.2，而分数阶PID控制时，除了开始时有点超调外，到车辆完全停止时，能基本稳定在0.2，没有波动，稳定性强。而在相同情况下，分数阶PID控制时，制动距离也相应减小不少。因此，设计的分数阶PID控制器，运用在汽车ABS中时的各项控制指标基本达到期望值。

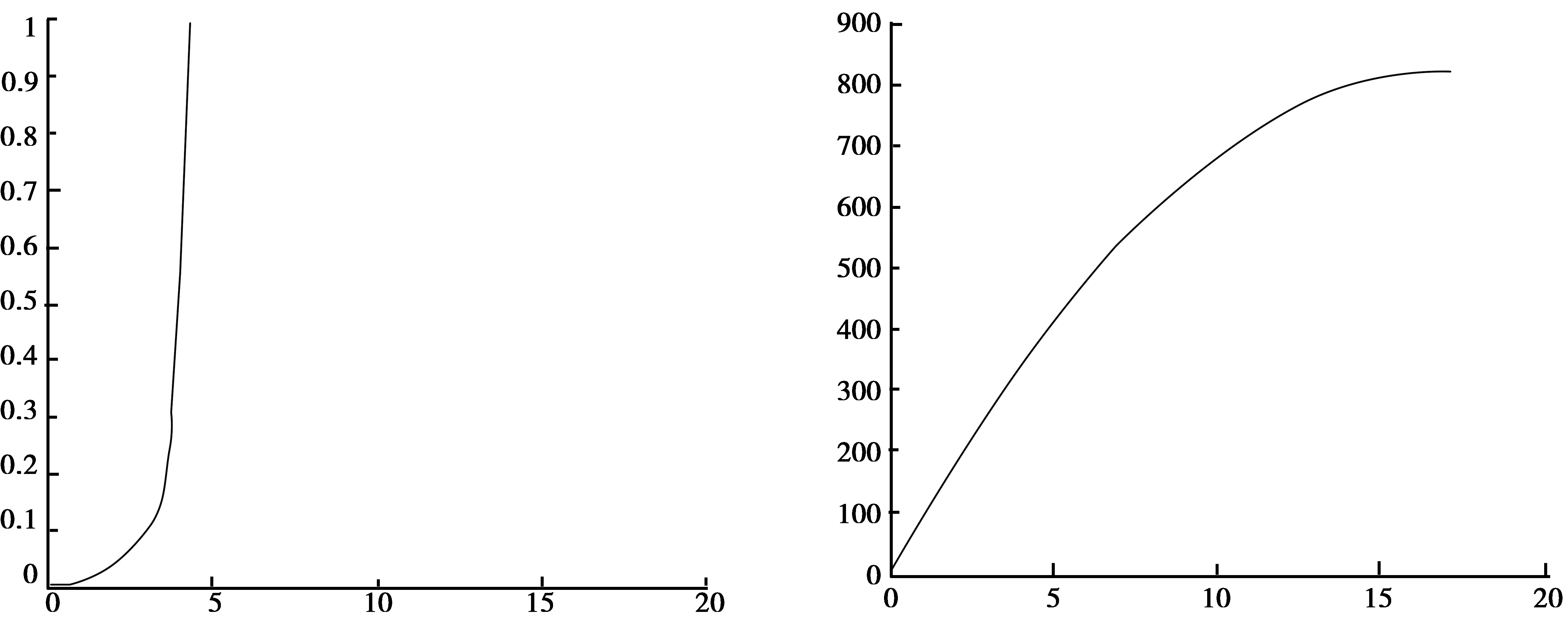
图6 无ABS情况下滑移率和制动距离曲线

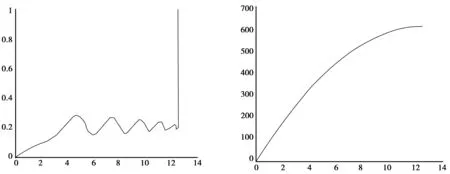
图7 ABS模糊控制器情况下滑移率和制动距离曲线

4 结 语

本文设计的基于分数阶PID控制的汽车ABS系统，能够使车轮的滑移率稳定的保持在正常情况下的0.2左右，且具有较快的响应速度和较好的稳定性，整体的控制效果优于传统的控制方法，因此，在以后的汽车ABS系统中可以考虑开发分数阶控制器。本文在使用Simulink建模时，进行了简化，这与实际系统之间存在一定差别；并且本文只是在单论模型上研究，不能反映出整车情形，因此在此基础上，建立更加精确的ABS半车模型或整车模型，以得到更反映实际情况的仿真结果。

参考文献：

[1] 程军.汽车防抱死制动系统的理论与实践[M].北京：北京理工大学出版社，1999

[2] 刘显贵，彭聪.防抱死制动系统滑模变结构控制研究[J].拖拉机与农用运输车，2009，36(1)：26-27，30

[3] 王铁，田立国，白雪峰.模糊PID控制在车辆制动过程中的应用[J].沈阳理工大学学报，2010，29(4)：17-21

[4] 张颖，袁朝辉.汽车防抱死系统的模糊PID控制算法研究[J].计算机仿真，2010，27(12)：312-315

[5] 罗佑新.新型分数阶PID控制器及其仿真研究[J].哈尔滨工业大学学报，2009，41(5)：215-217

[6] 袁幼成，周宗福，周辉.一类分数阶微分方程共振边值问题解的存在性[J].重庆工商大学学报：自然科学版，2012，29(3)：1-6

[7] 赵春娜，李英顺，陆涛.分数阶系统分析与设计[M].国防工业出版社，2011