关于不定方程 x3±64=67y2

董 小 倩

(西南大学 数学与统计学院，重庆 400715)

不定方程

x3±64=Dy2，x，y∈Z

(1)

(其中D为大于零的正整数)是一类基本而重要的不定方程，对它已有不少的研究工作.当D>2，D无平方因子且不能被3或6k+1的素数整除时，方程的解已经由文献[1]给出.但是当D为不含平方因子，并且能被3或6k+1的素数整除时，张攀[2]证明了当D=7，13，19，37，43时方程(1)的所有整数解.赵天[3]证明了不定方程x3+64=Dy2，当D=21时，则仅有整数解(x，y)=(-4，0)，(5，±3).牛芳芳[4]证明了不定方程x3-64=31y2仅有整数解(x，y)=(-4，0)，(20，±16)，(7，±3).而对于D=67时不定方程的解还未解决.此处在此基础上，利用同余式的性质和递归数列的方法，证明了该方程只有平凡解(x，y)=(∓4，0).

引理1[5]不定方程

x3+1=67y2，x，y∈Z

(2)

仅有整数解(x，y)=(-1，0).

定理1 不定方程

x3+64=67y2，x，y∈Z

(3)

仅有整数解(x，y)=(-4，0).

证明若x≡0(mod2)，则由式(3)有y≡0(mod4)，又由式(3)可知x≡0(mod4)，从而y≡0(mod8).设x=4x1，y=8y1，则式(3)化为x13+1=67y12，由引理1可知(x1，y1)=(-1，0)，故此时式(3)有解(x，y)=(-4，0).

当x≡1(mod2)时，式(3)化为(x+4)(x2-4x+16)=67y2，易知(x+4，x2-4x+16)=1或3，故式(3)有4种可能的分解：

情形1 x+4=67a2，x2-4x+16=b2，y=ab.

情形2 x+4=a2，x2-4x+16=67b2，y=ab.

情形3 x+4=3a2，x2-4x+16=201b2，y=3ab.

情形4 x+4=201a2，x2-4x+16=3b2，y=3ab.

以下分别讨论这4种情形所给式(3)的整数解.

情形1 由第二式得x=0，4，代入第一式都不成立，故该情形没有式(3)的整数解.

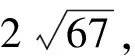
(4)

(5)

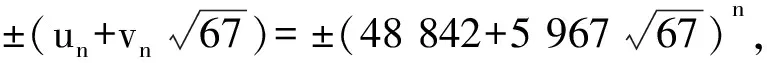
(6)

(7)

由式(6)得递推关系式xn+2=97 684xn+1-xn，x0=16，x1=1 581 050，故xn≡-1(mod17)，所以有xn+6≡5(mod17)，从而a2≡5(mod17)，而这不可能.

情形3和情形4 由于x≡1(mod2)，所以x2≡1(mod4)，代入第二式都有3b2≡1(mod4)，这不可能.故情形3和情形4都无解.

综合上述情形的讨论可得，不定方程x3+64=67y2，x，y∈Z，仅有整数解(x，y)=(-4，0).

引理2 不定方程

x3-1=67y2，x，y∈Z

(8)

仅有整数解(x，y)=(1，0).

定理2 不定方程

x3-64=67y2，x，y∈Z

(9)

仅有整数解(x，y)=(4，0).

证明若x≡0(mod2)，则由式(9)有y≡0(mod4)，又由式(9)可知x≡0(mod4)，从而y≡0(mod8).设x=4x1，y=8y1，则式(9)化为x13-1=67y12，由引理2可知(x1，y1)=(1，0)，故此时式(9)有解(x，y)=(4，0).

当x≡1(mod2)时，式(9)化为 (x-4)(x2+4x+16)=67y2，易知(x-4，x2+4x+16)=1或3，故式(9)有4种可能的分解：

情形1 x-4=67a2，x2+4x+16=b2，y=ab.

情形2 x-4=a2，x2+4x+16=67b2，y=ab.

情形3 x-4=3a2，x2+4x+16=201b2，y=3ab.

情形4 x-4=201a2，x2+4x+16=3b2，y=3ab.

以下分别讨论这4种情形所给式(9)的整数解.

情形1 由第二式得x=0，-4，都不满足x≡1(mod2)，故该情形没有式(9)的整数解.

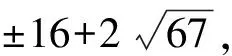
(10)

(11)

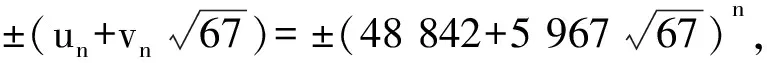
(12)

(13)

由式(12)得递推关系式xn+2=97 684xn+1-xn，x0=16，x1=1 581 050，故xn≡-1(mod17)，所以有xn-6≡10(mod17)，从而a2≡10(mod17)，而这不可能.

情形3和情形4 由于x≡1(mod2)，所以x2≡1(mod4)，代入第二式都有3b2≡1(mod4)，这不可能. 故情形3和情形4都无解.

综合上述情形的讨论可得，不定方程x3-64=67y2，x，y∈Z，仅有整数解(x，y)=(4，0).

参考文献：

[1] 张海燕，李复中.关于丢番图方程x3±64=Dy2[J].哈尔滨科学技术大学学报：自然科学版，1994，18(2)：107-109

[2] 张攀.关于不定方程x3±64=py2的研究[J].黑龙江大学学报：自然科学版，1992，19(2)：1-2

[3] 赵天.关于不定方程x3+64=21y2[J].重庆工商大学学报：自然科学版，2008，25(1)：09-10

[4] 牛芳芳.关于不定方程x3-64=31y2[J].重庆文理学院学报：自然科学版，2012，31(2)：32-33

[5] 王明军.关于丢番图方程x3+1=67y2[J].北华大学学报：自然科学版，2013，14(2)：150-151

[6] 杜先存，万飞，赵金娥.Pell方程ax2-by2=1的最小解[J].湖北民族学院学报：自然科学版，2012，30(1)：35-38