支架式教学：一个重要极限的抽象方法*

闻道君， 唐 艳， 陈义安

(重庆工商大学 数学与统计学院，重庆 400067)

1 支架式教学简介

在课堂教学方式的变革中，基于建构主义学习理论的支架式教学以培养学生自主学习能力的价值取向受到国内外广大教师和教科研工作者的青睐，成为课堂教学改革关注的热点。目前，国内对支架式教学的阐述大多从教育科学和课堂教学的宏观角度进行研究，很少从系统方法的角度对其进行微观思考，这使得支架式教学在具体学科中的教学实践相对滞后。从系统方法的视角看支架式教学，将支架式教学视作一个独立、有机运行的系统，需要先对该系统的本质及价值追求有一定的了解，然后才能在此基础上提出有效实施支架式教学的系统化策略。在支架式教学中，如何定位师生角色，创设合作式交流平台，开放教学情境以及协调教学要素对教学进行整体优化，并通过“教学支架”的适时建与撤实现学生思维自组织，最终建构自己的知识体系等系列问题，主要依赖于教育教学实践中教师的引导和支架功能，弱化教师的“知识输出”功能。支架式教学对教师传统的“传道、授业、解惑”功能提出了更高更具有挑战性的要求，不是对教师课堂教学作用的削弱，而是要求教师能高屋建瓴地驾驭课堂教学的方向。为了帮助学生建构属于自己的知识体系，教师不仅需要具备丰富的学科专业知识，更要具备将专业知识转化为面向学生的“教学知识”的能力。对高等教育而言，以培养具有创新能力的科技和应用型人才为己任，在“基础+专业”的培养模式下，如何优化各种教学资源促进“支架式教学”功能的实现就显得举足轻重。

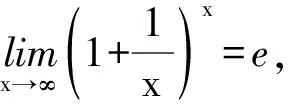
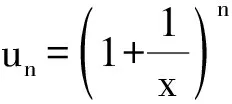
(1) 极限类型：1∞，说明该重要极限的类型以及可适用类型。

3 应用举例

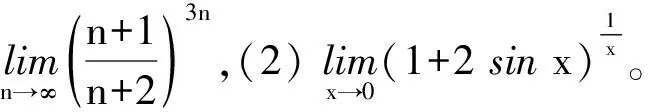
解(1) 由于极限类型为1∞，故先拆出常数1，然后在指数上构造无穷小量的倒数。

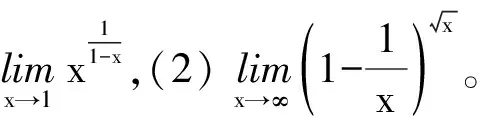
解(1) 由于极限类型为1∞，故先构造常数1(或换元)，然后在指数上构造无穷小量的倒数。

(或令t=1-x)

(2) 由于极限类型为1∞，故先按指数形式构造底数中的无穷小量，则

解(1) 由于极限类型为∞·0，故先转化为1∞，利用重要极限方法和函数的连续性，则

另外，如果利用等价无穷小量替换2x+3x2+4x3～2x(x→0)，求极限形式更为简洁。

(2) 由于极限类型为1∞，故先利用三角函数转化常数1，后在指数上构造无穷小量的倒数，则

参考文献：

[1] 龚德恩，范培华.微积分[M].北京：高等教育出版社，2008

[2] 李霄民，夏莉.微积分(上册)[M].北京：高等教育出版社，2010

[3] 陈文灯，袁一圃，俞元洪.高等数学复习指导[M].北京：北京理工大学出版社，1992

[4] 陈传璋，金福临，朱学炎，等.数学分析[M].2版.北京：高等教育出版社，1995

[5] 盛艳，张伟平.从系统方法的视角看支架式教学的实践[J].当代教育科学，2011(20)：38-40

[6] 盛艳，张伟平.新课改视野下的支架式教学：师生角色调适问题探讨[J].教学与管理，2012(8)：21-23

[7] 闻道君，龚黔芬.Simpson 不等式的改进及其应用[J].数学的实践与认识，2010，40(21)：159-162

[8] 闻道君，陈义安，唐艳.高等院校经管类专业的数学教学方法研究[J].重庆工商大学学报：自然科学版，2011，28(4)：413-416

[9] 李红婷.高师“数学教学论”课程建设的反思与重构[J].西南师范大学学报：自然科学版，2010，35(6)：196-200

[10] 江蓉，王守中.矩阵的秩在线性代数中的应用及其教学方法的探讨[J].西南师范大学学报：自然科学版，2012，37(8)：175-180