氢化锂热化效应机理研究

王立鹏，江新标，赵柱民，陈立新

(西北核技术研究所，陕西 西安 710024)

随着航天事业的飞速发展，空间核热推进和深空探测的持续能源供给已成为航天任务的重大课题。氢化锂(LiH)以其低密度、高熔点和相对较高的H原子份额等良好的热物性，被用于空间核热推进和动力装置的反应堆的最佳屏蔽材料和候选慢化剂材料[1]。然而，目前LiH热中子区的截面数据仍采用自由气体等简单模型的计算结果，导致在以LiH为慢化剂的反应堆临界计算中引起较大的系统误差，同时影响了该核装置的反应性温度系数等的计算结果，因此，需对LiH的热中子的核数据进行较详细的评价计算。热中子核反应堆中，能量低于4 eV的中子与散射核的热能相当，散射截面不单纯与中子能量变化有关，还与散射介质的温度及物理、化学性质有关，要精细研究LiH热中子散射截面数据就需仔细分析LiH的晶格参数等。本文对氢化锂热化效应机理进行研究。

1 LiH的慢化性能

轻元素具有较大的平均对数能降ξ，因此，常用慢化剂材料一般选用轻元素。此外，慢化剂还应具有较大的散射截面，为描述慢化剂材料对中子慢化的综合特性，引入该材料的慢化能力，慢化能力定义为ξΣs，Σs为宏观散射截面。另外，从中子损失的角度考虑，显然还要求慢化剂应具有较小的吸收截面，并引入慢化比，定义ξΣs/Σa为慢化比，其中，Σa为宏观吸收截面。性能良好的慢化剂不仅应具有较大的慢化能力，还应具有较大的慢化比。表1列出LiH与常用慢化剂材料的慢化性能[2]比较。ZrH2和LiH各元素均采用JENDL4.0库热中子的数据。可见，单纯就慢化性能而言，LiH慢化能力和慢化比均优于ZrH2，可作为慢化剂的候选材料。

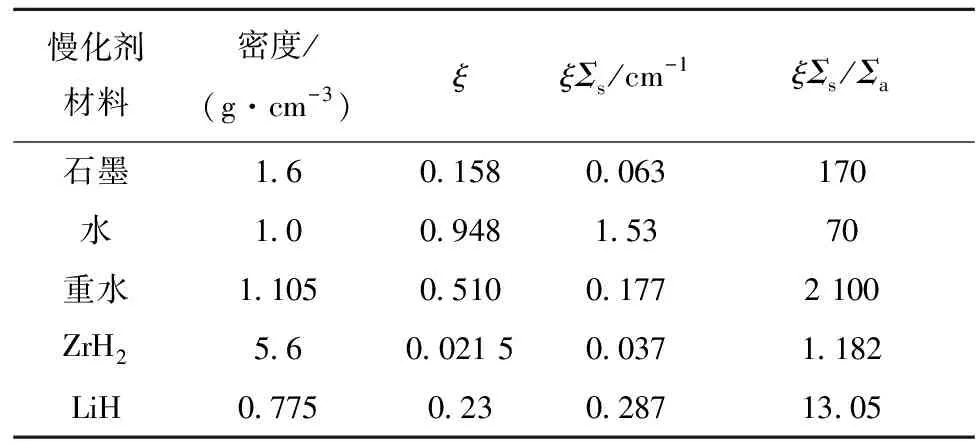
表1 LiH与常用慢化材料的慢化性能对比

2 声子谱制作

热中子的能量范围(1 eV以下)恰好是一般固体点阵振动的能量范围，因此考虑固体的热中子散射时，需考虑固体点阵振动的效应。研究单质固体点阵的振动多采用简谐近似，即假设固体中只存在一种原子，它们受到各向同性简谐力的作用。在简谐近似下的量子力学处理中，固体的元激发(振动)就是声子，因而，固体点阵振动对热中子散射的效应也就是声子效应[3]。金属氢化物中氢原子的三态振幅和单态振幅符号相反，散射几乎完全不相干(σ相干=1.8×10-24cm2，σ不相干=81.5×10-24cm2，σ为微观截面)，一般可当作全部是不相干散射来处理，即所谓不相干近似。

对于非单质组成的简单固体晶格，也可采用声子模型来处理。LiH晶格与NaCl相似，由Li+和H-结合而成，是一种典型的离子晶体，Li+构成一面心立方晶格，H-也构成相同的面心立方晶格，两个面心立方子晶格各自的原胞具有相同的基矢，由它们相套形成LiH复式晶格，结构如图1所示。国内外曾对ZrH2的声子谱进行过详细研究[4-6]，如LANL使用VASP+PHONON程序对材料的声子谱进行精细的晶格振动计算。本工作基于第一性原理方法，采用Materials Studio软件的CASTEP模块对LiH声子谱进行计算。第一性原理方法又称为从头算法，它将多原子体系当作由电子和原子核构成的多粒子体系，利用量子力学中的基本原理，在不引入任何实验参数的情况下对多原子体系进行处理。

图1 LiH基本晶格(a)和倒易空间(b)的结构

首先利用第一性原理方法计算程序CASTEP计算了LiH在基态时的能量与结构，交换关联函数使用Perdew等[7]提出的梯度密度修正近似(GGA)。赝势方法采用的是模守恒赝势，Li和H的截断能量选为800 eV，计算采用周期性超晶格方法，LiH立方相的Brillouin区积分在6×6×6的Monkhost-Pack格子中进行。计算的LiH声子谱及文献值[8]示于图2，声学项的贡献主要来自LiH中的Li，光学项主要来自H。计算的声子谱结果与红外测量的零阶声子展开得到光学项的横波和纵波频率(0.098 eV，0.13 eV)基本一致[9]，并在0.062～0.07 eV左右有一段声子项和光子项的能量缺口，声子谱为零。同时，本工作计算结果也与ZrH2中H和Zr的声子谱进行了对比，相较于ZrH2，LiH的声子项和光子项分隔的不太远，这主要是因为Li和H的原子质量相差不大，且出现两个特征光学项。

3 热中子散射截面计算

热中子散射截面的制作包括热散射律和热散射矩阵的计算。目前，国内外计算热散射律的软件有GASKET和NJOY/LEAPR，前者是较早期进行热中子散射律计算的工具，后者是前者的改进，且嵌入在通用截面处理程序NJOY的1个模块中。计算时采用各项同性简谐振动模型和高斯近似。非弹性散射和不相干弹性散射的表达式如下。

非弹性散射：

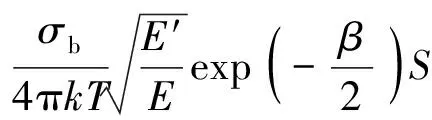
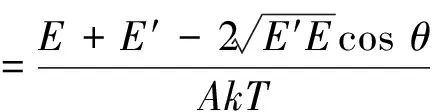
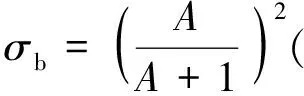
(1)

其中：α表征动量的变化；β表征能量的变化；σb为束缚态截面；σcoh为相干散射截面；σinc为不相干散射截面；Ω和Ω′为散射前后的立体角；E和E′为散射前后的能量；k为Boltzmann常数；T为温度；S(α，β)为热散射律；A为原子质量。

不相干弹性散射：

μ·

δ(μ)δ(E-E′)

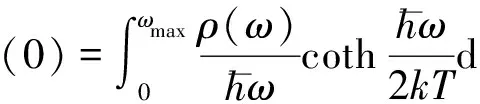
(2)

其中：μ为散射角余弦；δ(μ)为δ函数；γ(0)为Debye-Waller积分；ω为角频率；ρ为声子频谱。

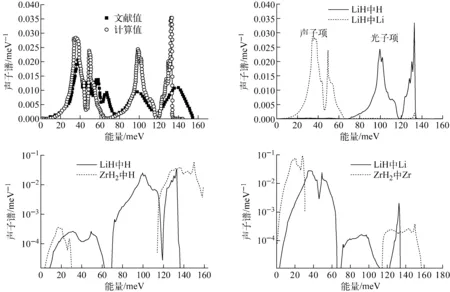
图2 LiH与ZrH2的声子谱

热散射律：

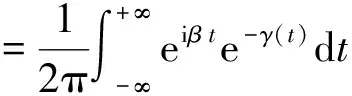
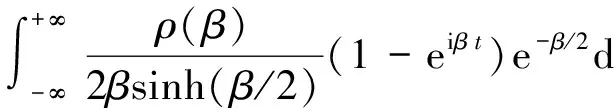
(3)

其中：t为时间特征量；ρ(β)为归一化后的声子谱。

已知ρ(β)，即可根据式(1)和(2)得到非弹性散射截面和不相干弹性散射截面。

可以表征不相干弹性散射截面的参数有两个，为Debye-Waller积分γ(0)和有效温度Teff：

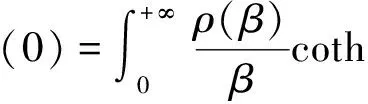
(4)

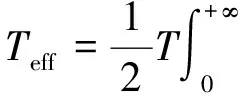
(5)

这两个参数均是温度的函数，它们与材料的热导率、比热容等物性参数密切相关，当温度高于Debye有效温度时，比热容随温度的变化很小。将GASKET或LEAPR得到的热散射律数据输入NJOY的THERMR模块，然后输出到特定格式的输出模块，如ACER模块，即可完成LiH热中子截面数据的制作和加工。

4 计算结果分析

4.1 散射截面数据比较

非弹性散射截面直接反映LiH的声子谱效应，图3示出300 K和800 K下LiH中H和Li的非弹性散射截面和ZrH2中H和Zr的非弹性散射截面。由图3可见，在低能区时，两者的H的非弹性散射截面类似，LiH中H比ZrH2中H的稍大，这主要是由于LiH中H在低能区的声子项比ZrH2中H的大，且LiH和ZrH2中的声子项比光子项小。随着温度的升高，H的非弹性散射截面变大，中子与LiH间的相互作用更易激发LiH的晶格态，中子从而获得LiH的声子能量。由图3a可看出，在大于0.1 eV之处，LiH和ZrH2中的H均表现出Einstein振子的特征，该位置即是H原子的结合能处，这一现象主要是因为H声子谱中的光学项的作用，由于LiH中H具有两个光学项，与声子项相隔不远，因此Einstein振子的特性没有ZrH2中H的明显。由图3b可见，因Zr原子质量比Li的大，非弹性散射中最大的能量损失较小，因此，在低能处(<0.01 eV)，即使ZrH2中Zr的声子项比LiH中Li的大，LiH中Li的非弹性散射截面还是比ZrH2中Zr的大。天然Zr中包含51.45%的90Zr、11.22%的91Zr、17.15%的92Zr、17.38%的94Zr和2.8%的96Zr，采用束缚核散射自由程模型[10]，得到的天然Zr的相干和不相干截面分别为6.44×10-24cm2和0.02×10-24cm2，其总和比7Li的0.619×10-24cm2和0.78×10-24cm2要大很多，而不相干散射截面最后要转化为自由核总散射截面，即自由气体模型模拟的截面。随着温度的升高，LiH中Li和ZrH2中Zr的非弹性散射截面差异变大，截面随着能量由大变小到由小变大的转折能量增大。

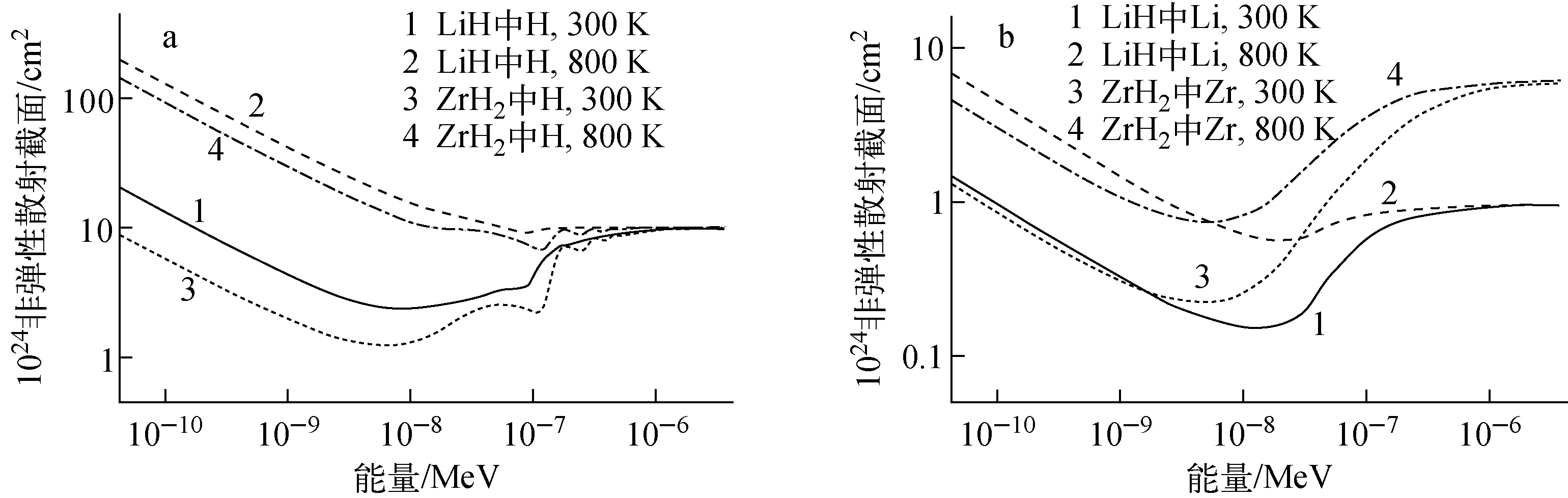
图3 LiH和ZrH2的非弹性散射截面

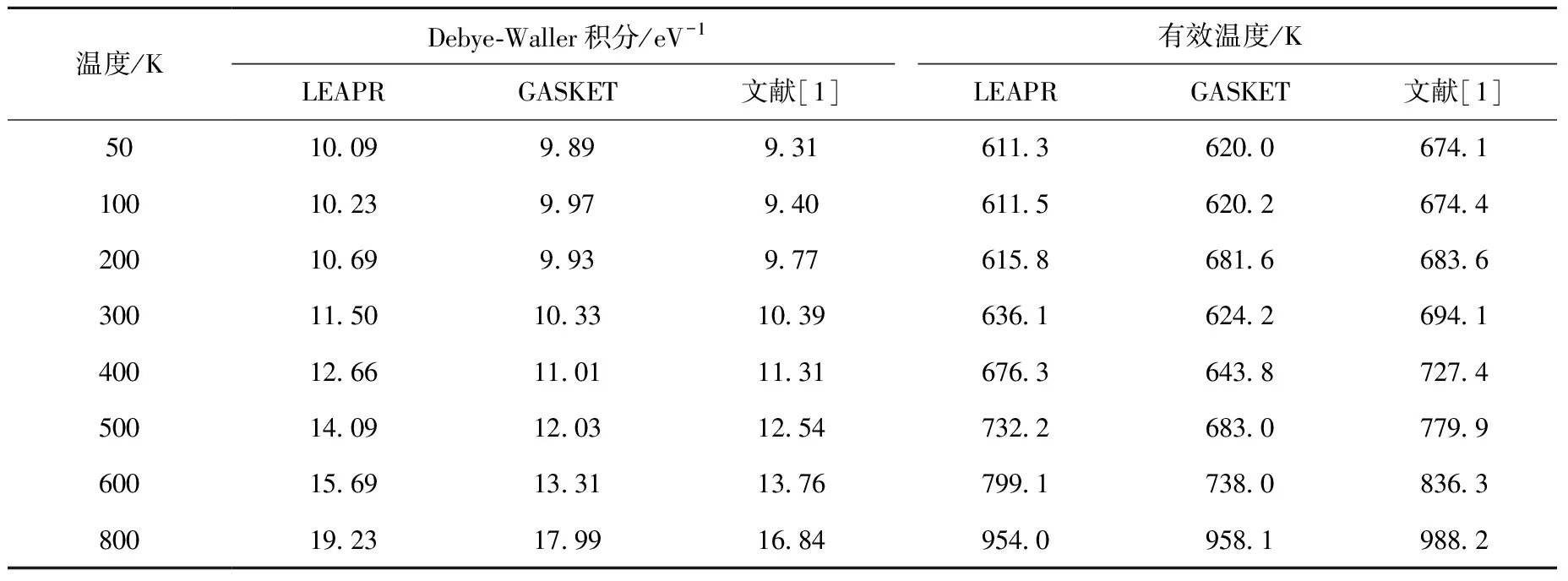
表2 LiH中H的Debye-Waller积分和有效温度与文献的对比

中子与LiH晶体发生碰撞时，除有非弹性散射外，还有弹性散射，将热散射律数据制作过程中产生的Debye-Waller积分和有效温度与文献值进行对比，结果列于表2。由表2可看出，Debye-Waller积分相较于有效温度的差异略小，这是因为LEAPR在GASKET程序的基础上采用了更高阶的声子谱展开，能够计算更大的能量转移和动量变化下的热中子散射律，考虑到早期ZrH2采用的是1/360权重的声子项，文献[1]认为LiH与ZrH2声学支权重之比几乎等于Li和Zr的原子质量之比，推导出LiH中H为1/28权重的声学项，进而采用GASKET得到热散射律。而本文是在密度泛函的理论下，采用第一性原理方法严格计算得到LiH中H的声子谱，使用LEAPR进行计算，且LEAPR在GASKET的基础上做了一些改进，得到的截面数据应更可靠。

4.2 次级中子能量分布

图4示出室温(300 K)下LiH非弹性散射的次级中子能谱分布。图4中，分别截取25.3、112、251和503 meV入射中子能量在全角度内的积分截面，得到相应的次级中子能谱，并对此进行抛物线修正，声子谱小于5 meV时服从Debyeω2分布。从图4可看出，抛物线修正主要减弱了入射中子能量处的最大峰值，使得截面更符合客观规律。中子与LiH发生非弹性散射时，由于LiH声子效应，次级中子可能获得或丢失1个或多个声子，从而伴随中子获得或损失能量。同时从图3可看出，随着温度的升高，靶核的激发态更易被激发，非弹性散射更易发生，中子更易获得能量，导致反应堆能谱变硬，影响中子产生率、中子泄漏率和中子吸收率等，该效应已在以ZrHx为慢化剂的TRIGA反应堆[6]和TOPAZ空间堆[11]中得到体现。

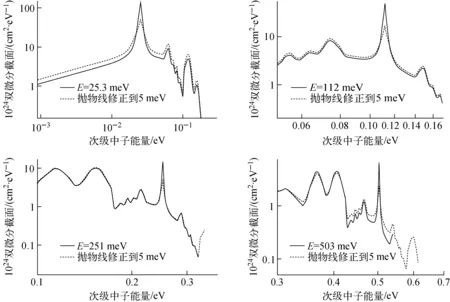
图4 不同入射中子能量下的次级中子能谱分布

5 结束语

本文研究了新型慢化剂材料LiH的热化效应，应用第一性原理方法计算LiH中H和Li的相关的晶格动力学参数，得到声子谱数据，以MCNP的ACE格式的热中子截面数据的制作为例，从LiH声子谱制作、热中子散射截面数据的制备入手，完成LiH热中子散射截面数据库的制备，分析次级中子能量的分布情况，为下一步以LiH为慢化剂的核热推进粒子球床堆的物理分析奠定基础。

参考文献：

[1] MUGHABGHAB S, SCHMIDT E, LUDEWIG H. Generation of neutronic thermal data in support of space nuclear propulsion[C]∥Tenth Symposium on Space Nuclear Power Systems. Albuquerque, New Mexico: [s. n.], 1993.

[2] 谢仲生，尹邦华. 核反应堆物理分析[M]. 4版. 北京：原子能出版社，2004：7.

[3] 贝尔G I，格拉斯S. 核反应堆理论[M]. 千里，译. 北京：原子能出版社，1979：226-240.

[4] MacFARLANE R E. New thermal neutron scattering files for ENDF/B-Ⅵ, Release 2, LA-12639-MS[R]. USA: LANL, 1994.

[5] MATTES M, KEINERT J. Thermal neutron scattering data for the moderator materials H2O, D2O and ZrHxin ENDF-6 format and as ACE library for MCNP(X) codes, INDC(NDS)-0470[R]. USA: [s. n.], 2005.

[6] 江新标，陈伟，陈达，等. 氢化锆中氢的散射律和散射矩阵研究[J]. 原子能科学技术，1999，33(2)：156-161.

JIANG Xinbiao, CHEN Wei, CHEN Da, et al. Study on the scattering law and scattering kernel of hydrogen in zirconium hydride[J] Atomic Energy Science and Technology, 1999, 33(2): 156-161(in Chinese).

[7] PERDEW J P, BURKE K, WANG Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system[J]. Phys Rev B, 1996, 54(23): 16 533-16 539.

[8] ZEMLIANOV M G, BROVMAN E G, CHERNOPLEKOV N A, et al. Inelastic scattering of neutrons[R]. Vienna: International Atomic Energy Agency, 1965.

[9] BEYSTER J R, BROWN J R, KOPPEL J U, et al. Integral neutron thermalization, GA-3542[R]. US: Atomic Energy Commission, 1962.

[10] SEARS V F. International tables for crystallography, Volume C: Mathematical, physical and chemical tables[M]. Dor-drecht/Boston/London: Kluwer Academic Publishers, 1992.

[11] 解家春，赵守智，贾宝山，等. TOPAZ-Ⅱ反应堆慢化剂温度效应分析[J]. 原子能科学技术，2011，45(1)：48-53.

XIE Jiachun, ZHAO Shouzhi, JIA Baoshan, et al. Analysis of moderator temperature effect for TOPAZ-Ⅱ reactor[J]. Atomic Energy Science and Technology, 2011, 45(1): 48-53(in Chinese).