平板形目标的量子雷达散射截面计算
林 云
(电磁散射重点实验室,上海 200438)
平板形目标的量子雷达散射截面计算
林 云
(电磁散射重点实验室,上海 200438)
介绍了一种可以用于平板形目标的基于解析光子波函数的量子雷达散射截面计算方法。与之前相关研究中提出的方法相比,该方法避免了在球面上对一个剧烈变化的积分核的数值积分。该方法数值效率比相关文献中给出的方法高,并且可以用于任意形状的理想导体平板的量子雷达散射截面的仿真。
量子雷达;雷达散射截面;光子波函数
0 引言
近年来,量子信息科学的分支量子通信和量子计算得到了长足的发展。处于量子纠缠态的微粒被用于保密通信;具有350个量子比特的量子计算机已被实现[1]。Shor算法和Grover算法等量子算法展现出比传统算法更高的效率[2,3]。这些量子信息科学的最新进展也为量子探测的发展奠定了基础。将纠缠态微粒使用在雷达系统中,从而实现一部雷达同时工作在多模式下的想法是量子雷达的最初概念[4]。量子雷达的概念提出至今不到十年时间,实现中还有很多问题需要研究。比如量子雷达的系统构成、其发射机和接收机的设计、信道描述和信号处理方法、散射截面分析方法等。其中,量子雷达散射截面的研究与其系统实现无关,而且是系统设计的重要输入参数,急需深入研究,但目前相关的研究较少。
2012年,美国ITT公司的Marco在文献[5,6]中给出了量子雷达散射截面的定义,并且从定义出发给出了一种可以实现的算法。采用该方法Marco给出了矩形理想导体平板的量子雷达散射截面的数值计算结果,但该方法由于需要在球面上计算一个剧烈变化的积分核的数值积分,计算效率较低,仅用于很小的系统量子雷达散射截面的模拟。
本文利用光子波函数和量子雷达散射截面的定义推导了量子散射截面的计算公式。相比于已有文献中给出的计算方法,本方法有更高的计算效率。通过量子雷达散射截面的数值算例,讨论了本算法的正确性和有效性。
1 理论及公式
与传统的雷达散射截面类似,量子雷达散射截面σQ可以定义为目标在量子化的电磁场照射下的散射场强度和入射场强度的比值,并用球面波扩散因子归一化[5]。



其中:
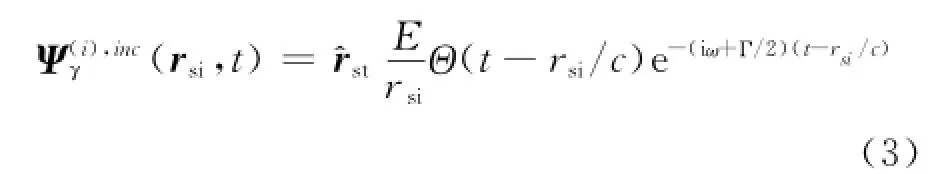
同理,利用光子波函数的定义,散射场强度可表示为
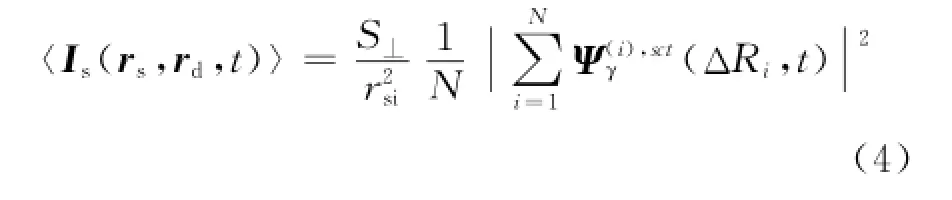
其中:

式中:S⊥为目标垂直于入射方向的表面积;为散射场光子波函数;ΔRi为目标与雷达之间的来回总路程;为目标指向雷达的单位矢量。
量子雷达散射截面σQ可表示为
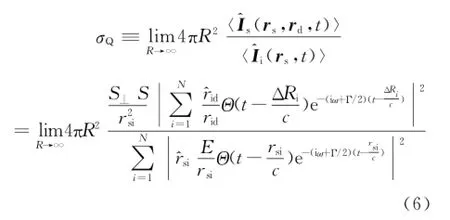
具体推导过程见参考文献[6]。对于量子雷达散射截面的计算,满足远场条件,可用远场条件rid≈rsi≈R对式(6)进一步简化,得

文献[5]中给出的量子雷达散射截面的计算式为

比较式(7)与式(8),可以发现式(8)中分母部分是一个剧烈变化的积分核在球面上的数值积分。该积分的计算需要非常多的积分点才能获得良好的精度,这意味着需要大量的计算时间。而采用式(7)则可以避免这个问题,从而加快计算的速度。而且文献[5]中仅仅给出了矩形平板的量子雷达散射截面的数值结果,而式(7)则可以适用于任意形状的平板结构的量子雷达散射截面的仿真。
2 数值算例
用几个数值算例来分析本文提出的算法的正确性和高效性。首先为了验证程序的正确性,用本文提出的算法计算了一个理想导体矩形平板的单站量子雷达散射截面。该矩形平板的尺寸长为4λ,宽为2.5λ,(λ为入射光子的波长,文中取1 m)。该矩形平板用100 000个微粒模拟,具体的设置如图1所示,该理想导体平板处于xoy平面,入射面为yoz平面,入射光子的传播方向与z轴的夹角为θ。

图1 理想导体平板的单站雷达散射截面示意图
采用文中给出的方法计算该理想导体平板的量子雷达散射截面,数值结果如图2所示。
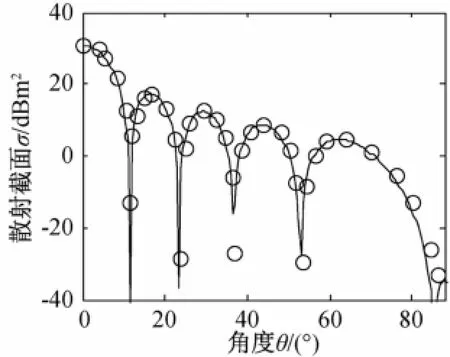
图2 矩形平板的单站量子雷达散射截面
由图2中可以看出采用本文给出的方法得到的计算结果(实线)和文献[6]中给出的结果(圆圈所示)吻合较好。在计算速度方面,这个算例是在一台配置了Intel 3.0 GHz CPU的台式微机上完成仿真的,计算总耗时仅5.6 s。而据文献[6]中的报道,在一台Intel 1.4 GHz CPU的电脑上仿真一个由单光子和10 000微粒构成的量子系统,耗时约4 h。由此可见,本算法大大加快了量子雷达散射截面的仿真速度,提升了对复杂量子系统仿真的能力。
由图3中可以看出,金属平板的量子雷达散射截面(实线)和传统雷达散射截面(十字所示)的趋势相似,但在副瓣位置出现较大的区别。

图3 单站量子雷达散射截面与量子雷达散射截面比较
本文给出的方法可以用于任意形状的理想金属平板的量子雷达散射截面的仿真。为验证这一点,将测试椭圆形理想导体平板的量子雷达散射截面。该椭圆平板的长半轴为20λ,短半轴为10λ。考虑单光子入射情形的单站量子雷达散射截面。仿真的结果如图4所示,传统雷达散射截面是通过物理光学方法获得的。
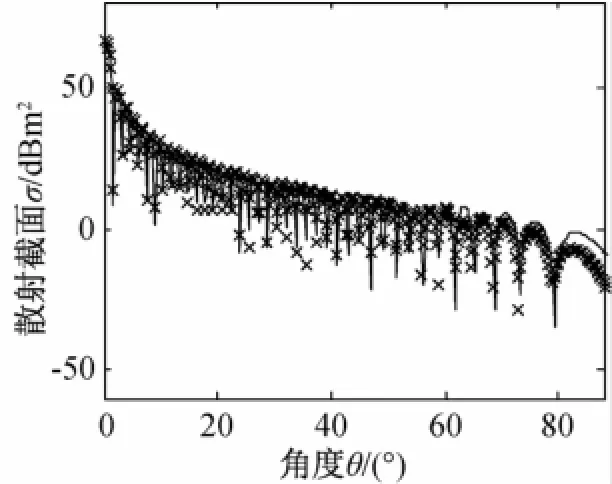
图4 椭圆形平板的雷达散射截面
3 结论
本文基于量子雷达散射截面和光子波函数的定义推导给出了一种可以快速有效计算量子雷达散射截面的方法。利用该算法成功求解了矩形及椭圆形理想金属平板的量子雷达散射截面,具有良好的数值精度和较高的计算速度。
[1]Peter W.Shor.Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quanturn Computer[C].Proceeding of the 35th Annual Symposium of Foundations of Computer Science,IEEE Computer Society Press,1994:124-134.
[2]L.Grover.Quantum Mechanics Helps in Searching for a Needle in a Haystack[J].Physics Review Letter,1997,79(23):325-328.
[3]E.H.Allen,M.Karageorgis.Radar Systems and Methods Using Entangled Quantum Particles[R]. US Patent 7375802,2008.
[4]Marco Lanzagorta.Quantum Radar[M].USA: Morgan&Claypool Publishers,2011.
[5]Marco Lanzagorta.Quantum Radar Cross Sections[J].Proceedings SPIE,Quantum Opics,2010, 7727.
[6]Yun Lin,Liangshuai Guo,Kun Cai.An Efficientalgorithm Fir the Caculation of Quantuam Radar Cross Section of Flat Objects[C].PIERS,PIERS Proceeding,2014: 39-43.
Calculation of Quantum Radar Scattering Cross Section of Flat Structures
LIN Yun
(Science and Technology on Electromagnetic Scattering Laboratory,Shanghai 200438,China)
This paper proposed an alternative way for simulation quantum radar scattering cross section of flat objects.The presented method is based on the analytical photon wave function.Compared with previous studies,the presented method avoids the evaluation of an integral of a rapid changing pattern on a spherical surface.Thus the proposed method is more computational efficient,and is able to simulate the quantum radar cross section of arbitrary shape flat structures.
quantum radar;radar scattering cross section;photon wave function
TN011
A
1671-0576(2014)04-0050-04
2014-08-13
林 云(1981―),男,博士,工程师,主要从事计算电磁学研究。
——2022 F1意大利大奖赛

