电磁波旋转器的散射特性及参数分析

庞旭东, 柳志娟, 朱伟华, 朱守正

(1.上海机电工程研究所,上海 201109;2.上海宇航系统工程研究所,上海 201109; 3.华东师范大学信息科学与技术学院,上海 200241)

电磁波旋转器的散射特性及参数分析

庞旭东1, 柳志娟2, 朱伟华1, 朱守正3

(1.上海机电工程研究所,上海 201109;2.上海宇航系统工程研究所,上海 201109; 3.华东师范大学信息科学与技术学院,上海 200241)

首先介绍了电磁波旋转器的理论基础并做简要验证；其次利用有限元法电磁仿真软件对90°旋转器的电磁散射性能进行了仿真验证与定量计算；然后对旋转器参数极值及分布范围随器件偏转角度的变化情况进行了详细分析；最后提出了旋转集中器和旋转扩展器两种复合器件模型。

变换电磁学；超材料；散射宽度；参数分析

0 引言

在变换电磁学中,利用坐标变换的方法［1］,可以根据需要设计特定介质,使得电磁波在这些介质中以期望的方式进行传播或散射,从而达到对电磁波的操控［2,3］。结合超材料(Metamaterial)技术,可以设计出多种新颖的器件。最早的应用是电磁隐身斗篷［4］,其后从隐身器件的研究中迅速发展了其它功能的变换电磁学器件,比如电磁波集中器［5-7］、电磁波扩展器等［8］,这些器件都是由径向坐标变换得到的。本文将讨论一种由角度变换得到的器件——电磁波旋转器［8-10］。

1 理论基础

电磁波旋转器是由角度坐标变换得到的变换电磁学器件［8-10］,图1中的器件模型选取了二维圆柱模型［5］,图中模型所选边界横坐标以x(m)表示,纵坐标以y(m)表示。内圆(r=a)是器件的内边界,外圆(r=b)是器件的外边界,从z分量表面的电场分布可知不同偏转角的电磁波旋转器散射特性的仿真结果。

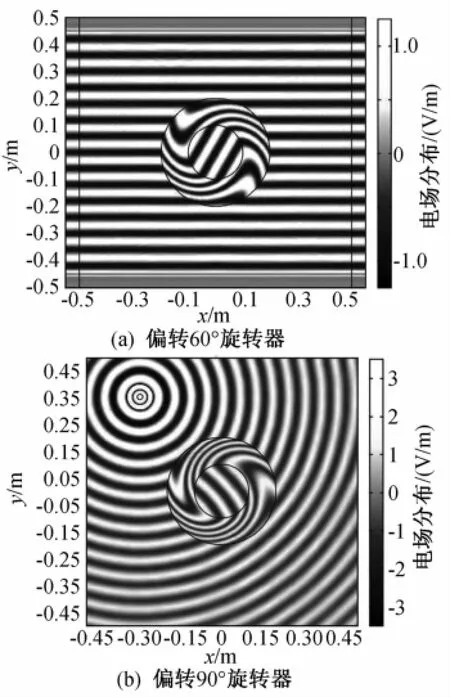
图1 不同偏转角的电磁波旋转器仿真图

在柱坐标系中,旋转器的坐标变换关系［9］:

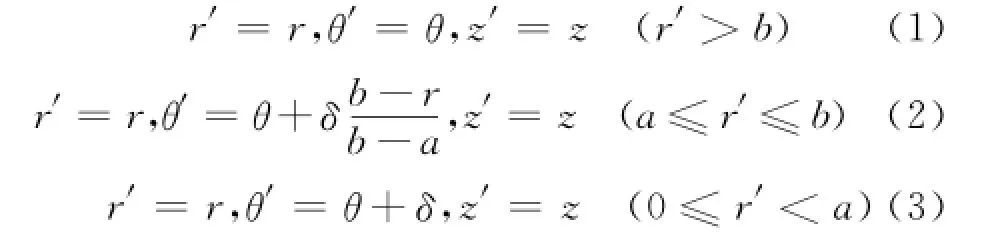
式中:δ为旋转器的偏转角度。外部空间的入射波经过旋转媒质a≤r′≤b的偏转后,在器件内部0≤r′≤a区域被逆时针旋转了δ角度。图1(a)是频率f=5 GHz的TE平面波入射时,偏转角δ =60°旋转器的仿真图;图1(b)是频率f=5 GHz距离d=0.461 m的柱面波入射时,偏转90°旋转器的仿真图。器件模型尺寸a=0.1 m,b=0.2 m,采用的仿真软件是Comsol Mutiphysics。

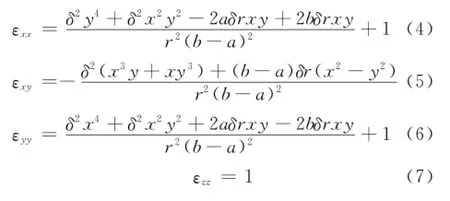
2 旋转器散射特性

由图1中可知,外部入射波经过旋转媒质偏转后,在器件内部区域被旋转了δ角。推论:对于放置于旋转器内部0≤r′≤a区域的内置物体,其散射模式将等效于此物体偏转δ角后的散射模式。

下面结合具体的仿真模型实例进行验证。图2是对内置PEC横板的90°电磁波旋转器电磁散射性能的仿真结果。设置参数:旋转器模型a= 0.1 m,b=0.2 m,δ=90°,内置PEC横板长0.16 m、宽0.01 m,频率f=5 GHz的TE平面波由上往下入射。图2(a)是将PEC平板横向放置于旋转器内部区域中心时,整体的散射效果;图2(b)是PEC平板纵向放置于中心位置时的散射效果;图2(c)是PEC平板横向放置于中心位置时的散射效果。

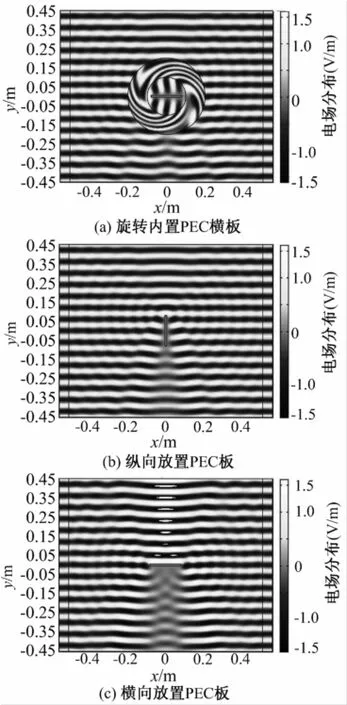
图2 对内置PEC横板的90°旋转器电磁散射性能的仿真

为便于定量比较,对图2三种情况中PEC平板的散射宽度值进行了计算［11］。由于用有限元法计算的结果是近场数据,需要运用Huygens原理将近场数据转化为远场数据,再计算散射宽度。计算公式是。图3(a)、图3(b)、图3(c)分别是图2(a)、图2(b)、图2(c)中PEC平板的散射宽度计算结果。图3的横坐标是方向角度;纵坐标是散射宽度值,统一采用(0～0.8)m的取值范围。从图2和图3可以发现:横向放置于旋转器内部的PEC平板散射模式基本等效于其纵向放置(旋转δ=90°)时的散射模式,且远小于横向放置时的散射模式,从而验证了前文的推论:对于旋转器内部的内置物体,其散射模式将等效于此物体偏转δ角后的散射模式。

上述散射模式的旋转变化也是幻觉电磁学的研究内容之一［12］。在军事领域,电磁波旋转器具有一定的干扰和迷惑作用,与其它变换电磁学器件配合使用具有进一步的应用价值。

3 旋转器的参数分析

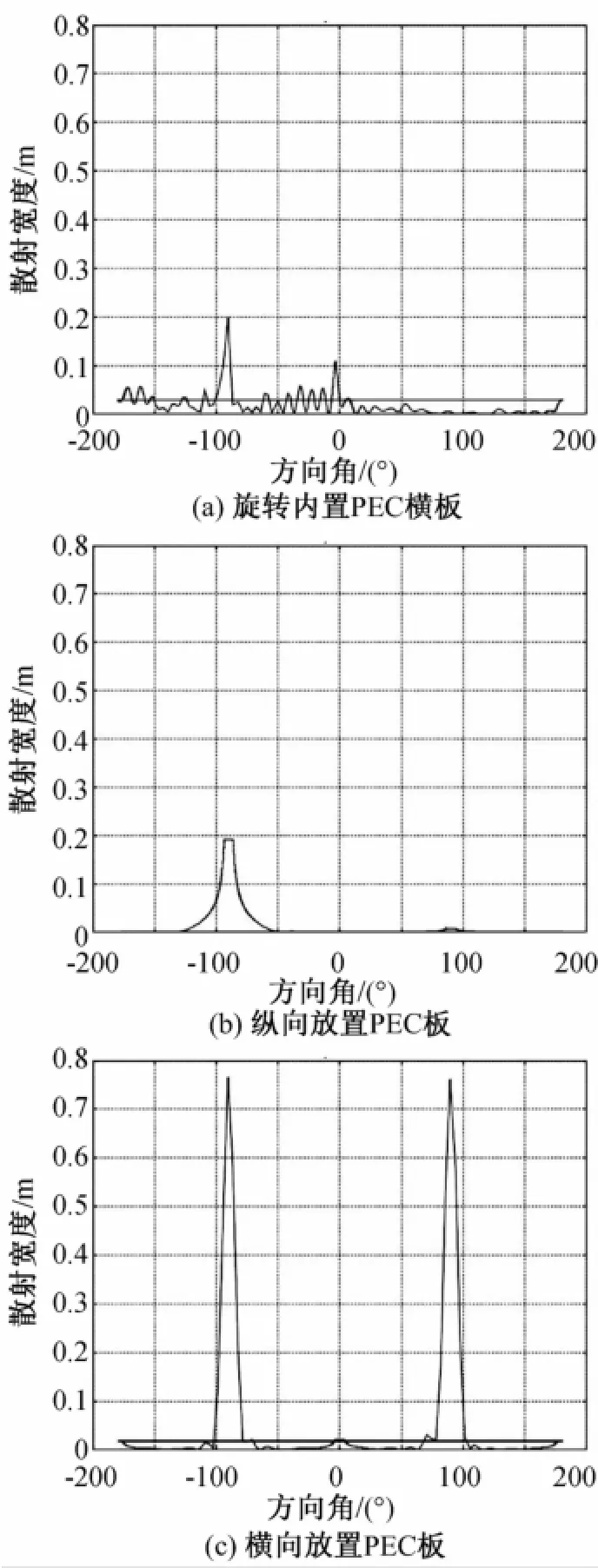
图3 对图2各情况下PEC平板散射宽度值的计算结果

下面分析电磁波旋转器材料参数极值随偏转角δ的变化情况,以及整体的分布规律。z方向材料参数保持1不变,为了具体表示x x、xy、yy方向参数分量极值与偏转角δ的定量关系,计算采集了多组数据,并绘制成散点曲线图。计算模型为图1中的旋转器模型,a=0.1 m,b=0.2 m, δ∈［0,360°］。

图4是x x、y y方向ε分量极值随δ变化的曲线,由于纵轴数值大小的差别,由图4(a)与图4 (b)表示。图4(a)中曲线表示εxxmax=εyymax,纵轴值分布较大,曲线随着偏转角的增加而上升;图4 (b)中曲线表示εxxmin=εyymin,纵轴值分布较小,曲线随偏转角的增加而下降。

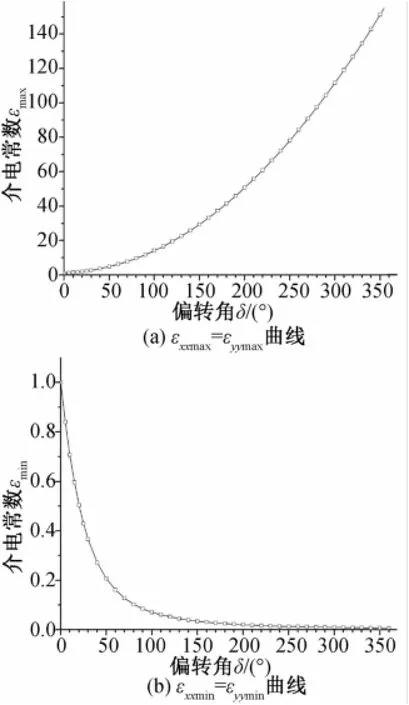
图4 xx、y y方向ε分量极值随δ变化的曲线

图5是x y方向ε分量极值随δ变化的曲线,图中虚线表示εxymax,实线表示εxymin。由于εxymax=―εxymin,所以虚线和实线曲线上下对称,其绝对值随δ增加而增大。

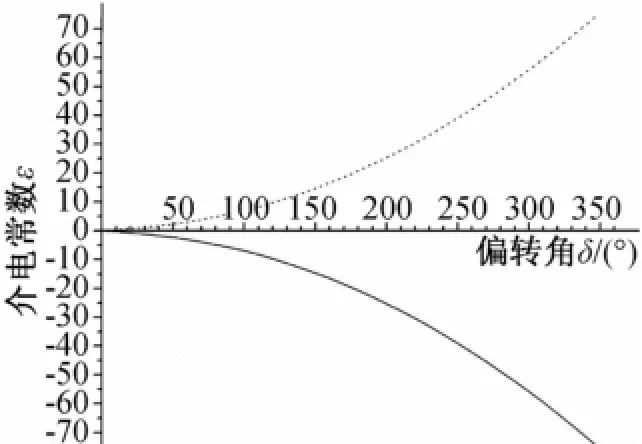
图5 xy方向ε分量极值随δ变化的曲线

在图6中,首先定义归一化参数分布范围: η=(εmax―εmin)/εmax×100%。这样xy方向的归一化参数分布范围就是200%。根据图4的数据,经过计算整理可以进一步得到x x和yy方向的归一化参数分布曲线,如图6所示。图中曲线随着δ的增加而迅速上升,表明随着旋转器偏转能力的提高,x x、yy方向所需材料参数的分布范围在不断增大,意味着材料实际实现的难度在不断增加。

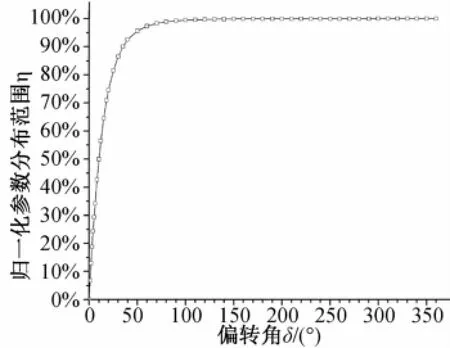
图6 xx、yy方向的归一化参数分布曲线

4 旋转器与其它器件的结合

可以将径向坐标变换(电磁波集中/扩展器)与角度坐标变换(电磁波旋转器)相结合,这样可以得到复合型变换电磁学器件。图7(a)与图7 (b)分别是90°旋转集中器与90°旋转扩展器的仿真示意图。通过径向/角度的复合变换,可以进一步得到多种新型的变换电磁学器件模型。

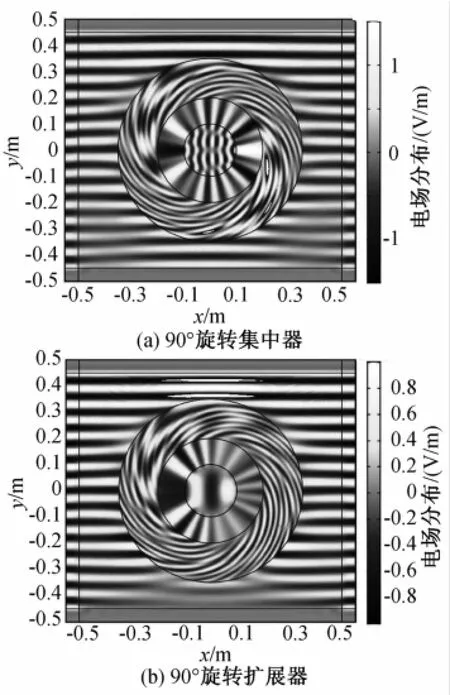
图7 旋转集中/扩展器仿真示意图

5 结论

本文在电磁波旋转器的理论基础上,通过对内置PEC横板的旋转器散射性能的研究验证了以下结论:对于旋转器内部的内置物体,其散射模式将等效于此物体偏转δ角后的散射模式;其次通过对旋转器的参数分析,发现随着器件偏转能力的提高,所需材料参数的分布范围在不断增大;最后提出了旋转集中器和旋转扩展器这两种新型复合器件模型,在军事领域具有进一步的干扰与迷惑作用。

［1］Leonhardt U.Optical Conformal Mapping［J］. Science,2006,312:1777-1780.

［2］Pendry J B,Schurig D,Smith D R.Controlling E-lectromagnetic Fields［J］.Science,2006,312: 1780-1782.

［3］Ting-hua Li,Jing-jing Yang,Ming Huang,etc. Arbitrary Control of the Electromagnetic Field in Two-dimensional Waveguide and Slit Using Metamaterials［J］.Appl Phys A,2011,105:509-515.

［4］Schurig D,Mock J J,Justice B J,etc.Metamaterial Electromagnetic Cloak at Microwave Frequencies［J］.Science,2006,314:977-980.

［5］Kuang Zhang,Qun Wu,Jia-hui Fu,etc.Cylindrical Electromagnetic Concentrator with Only Axial Constitutive Parameter Spatially Variant［J］.J. Opt.Soc.Am.B,2011,28(6):1573-1577.

［6］Li W,Guan J,Wang W.Homogeneous-materialsconstructed Electromagnetic Field Concentrators with Adjustable Concentration Ratio［J］.Journal of Physics D:Applied Physics,2011,44(12):125401.

［7］T.Li,M.Huang,J.Yang,etc.Three Dimensional Electromagnetic Concentrators with Homogeneous Material Parameters［J］.Progress In Electromagnetics Research M,2011,18:119-130.

［8］H.Chen,C.T.Chan,P.Shen.Transformation Optics and Metamaterials［J］.Nature Mater, 2010,9(5):387-396.

［9］Chen,Hua-yang C.T.Chan.Transformation Media that Rotate Electromagnetic Fields［J］.Applied Physics Letter,2007,90(24):241105.

［10］Luo Y.,Chen H.,Zhang J.,et al.Design and Analytical Full-wave Validation of the Invisibility Cloaks,Concentrators,and Field Rotators Created with a General Class of Transformations［J］. Physical Review B,2008,77:125127.

［11］Ralf Gente,Christian Jansen,Robert Geise,etc. Scaled Bistatic Radar Cross Section Measurements of Aircraft with a Fiber-Coupled THz Time-Domain Spectrometer［J］.IEEE Transactions on Terahertz Science and Technology,2012,99:1-8.

［12］Lai Y,Ng J,Chen H,et al.Illusion Optics:The Optical Transformation of an Object into Another Object［J］.Physical Review Lelters,2009,102 (25): 253902.

Scattering Characteristics and Parameter Analysis of Electromagnetic Wave Rotator

PANG Xu-dong1, LIU Zhi-juan2, ZHU Wei-hua1, ZHU Shou-zheng3
(1.Shanghai Institute of Electro-Mechanical Engineering,Shanghai 201109; 2.Aerospace System Engineering Shanghai,Shanghai 201109; 3.School of Information Science and Technology,East China Normal University,Shanghai 200241,China)

First the basic theory of electromagnetic wave rotator is introduced and a brief verification is given.Next numerical simulation and quantitative calculations are performed to demonstrate the scattering characteristics of the 90°rotator,and then the variation status of each parameter extremum and its distribution range with respect to the deflection angle of rotator is analyzed in detail.Finally two composite models of rotary concentrator and rotary expander are proposed.

transformation electromagnetics;metamaterial;scattering width;parameter analysis

TN011

A

1671-0576(2014)04-0029-04

2014-09-05

国家自然科学基金资助项目,编号61172032。

庞旭东(1984―),男,博士,工程师,主要从事超材料理论及应用、微波暗室性能分析及射频制导目标系统仿真技术研究。