一种小擦地角下空时相关的海杂波仿真模型
王佳宁, 许小剑
(北京航空航天大学,北京 100191)
一种小擦地角下空时相关的海杂波仿真模型
王佳宁, 许小剑
(北京航空航天大学,北京 100191)
提出一种距离和时间二维相关的复海杂波序列生成模型。该模型利用记忆非线性变换(MNLT)生成海杂波高分辨率距离像(HRRP),其满足空间-时间二维相关特性,且幅度服从Pareto分布;随后依据多普勒频率与HRRP幅度的近似线性关系,生成各个距离分辨单元中杂波序列的多普勒谱;最终利用交替投影(AP)算法反演出海杂波复散射信号的相位信息,从而得到符合特定统计特性和空间时间相关特性的二维复海杂波序列。仿真结果表明,本文提出的海杂波生成模型可有效生成幅度服从Pareto分布,距离和时间上相关,且各个距离单元内时间相关特性与相应单元内海杂波强度有关的海杂波序列。
空时相关;小擦地角;Pareto分布;多普勒谱;海杂波
0 引言
海杂波在海洋检测、海面目标检测与识别等方面具有重要影响[1-3]。高速有效地产生符合特定幅度分布和相关特性的海杂波序列,可为复杂海背景下目标回波特性的数据采集、特征提取等提供必要的技术支持,对相关武器装备在时变海背景下的仿真和评估具有重要意义。
海杂波的幅度分布模型主要是对海杂波的时间序列进行统计,得到其概率密度函数。当雷达分辨单元很高且擦地角较小时,海杂波回波信号中会出现“尖峰”现象[1,4],海杂波幅度的概率密度函数中长拖尾现象极其严重,常用的K分布等统计模型已无法较好描述这种具有尖峰特性的杂波。Pareto分布模型的概率密度函数具有长拖尾现象[5-6],可较好描述小擦地角下的海杂波,且其数学形式简单,近年来得到了较多关注。海杂波的空间相关特性一般由空间自相关函数描述,且与海面结构有关。时间上的相关性通常可由多普勒谱来描述。研究表明,不同距离单元内海杂波的多普勒特性不尽相同,且多普勒中心频率与海杂波的高分辨距离像(HRRP)呈近似线性关系[7-9]。
本文基于小擦地角下海杂波的空间和时间相关特性,提出了一种空时联合相关海杂波生成模型。该模型利用MNLT得到二维的Pareto分布随机矩阵,视其为各脉冲下海杂波HRRP构成的矩阵,并依据海杂波各个距离分辨单元中多普勒特性与HRRP的对应关系,生成各个距离分辨单元中的多普勒谱,最后利用AP算法计算对应的海杂波复散射信号的相位信息。最终输出的海杂波复散射信号幅度具有海尖峰,其功率谱与给定多普勒谱足够相似。
1 Pareto统计模型
Pareto分布模型为一种复合调制模型。对于服从Pareto分布的随机变量z,其概率密度函数为[5-6]
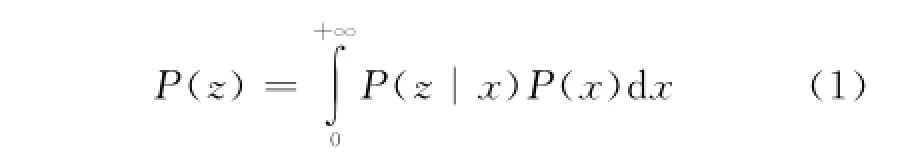
式中:x为海杂波的纹理分量,服从形状参数为a、尺寸参数为b的逆伽马分布,其概率密度函数为

海杂波的散斑分量服从负指数分析,并且受到纹理的调制作用,其概率密度函数为
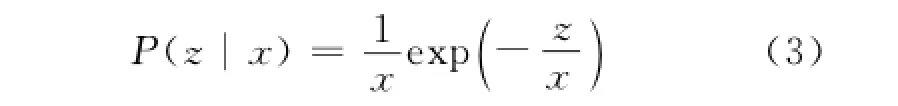
将式(2)和式(3)代入到式(1)中,得到Pareto分布的概率密度函数PDF为
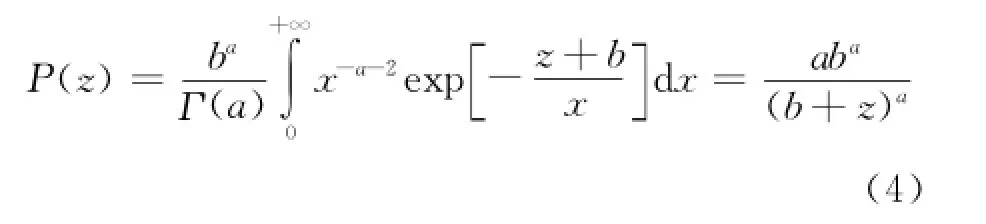
Pareto分布的概率累积密度函数CDF为

图1为文献[10]中,VV极化下海杂波实测数据,利用Weibull分布模型、对数正态分布模型、K分布模型和Pareto分布模型对其进行拟合得到的CDF。
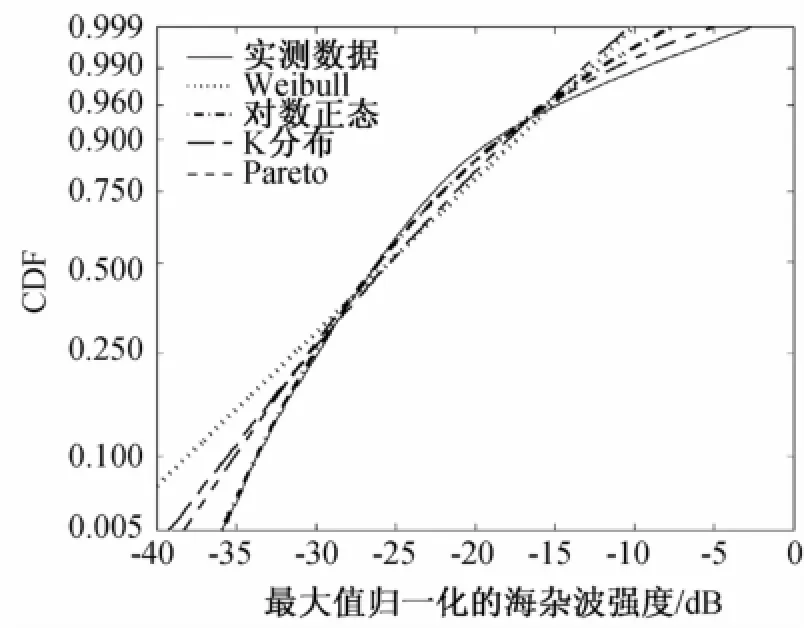
图1 测量数据及不同分布模型拟合下的海杂波CDF
由图1可见,Pareto分布能够较好地描述小擦地角下的海杂波统计分布特性。
2 小擦地角下海杂波的空时相关特性
(1)海杂波的空间相关特性
海杂波的空间相关特性由海杂波的调制过程和海表面轮廓之间的关联所产生。Watts等人认为:作为调制过程的海杂波的纹理分量在不同空间分辨单元之间是相关的,而海杂波的散斑分量从一个空间分辨单元到另一个空间分辨单元之间是完全不相关的[11]。
通常,海杂波幅度的空间相关函数Rs可用指数衰减函数来描述[11-12],表示为
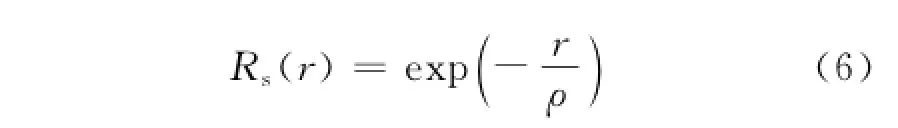
式中:ρ为海杂波相关距离的长度,可由经验公式获得

式中:U为海面上空的风速;g0为重力加速度常数;φ为风向与雷达视线之间的夹角。可见,海杂波随距离变化的空间相关特性由海面环境参数决定,风速越大时,海杂波的空间相关程度越强烈。在较短的时间间隔下,海面的环境参数可以视为是不变的。因而,雷达在较短观测时间下,接收到的不同脉冲中的海杂波序列的空间相关特性也是相同的。
(2)海杂波的时间相关特性
复海杂波时间序列的相关特性可由多普勒谱反映。近两年来,随着对海杂波相关特性研究的深入,学者发现不同距离单元内海杂波的多普勒谱不同,甚至会出现很大差异。Johnson等通过电磁计算得到了小擦地角下(0.46°~1.56°)海杂波的距离像和其在各个距离单元下的多普勒谱[7-8],并将各个距离单元下海杂波多普勒中心频率、海面距离像与海面高度起伏做了比较,发现各距离单元下多普勒中心频率构成的曲线、海面距离像、与海面高度起伏三者之间具有很高的相似度。Ritchie等对实测数据中小擦地角下海杂波的多普勒谱进行了分析[9],发现多普勒中心频率与杂波的强度近似呈线性关系。
本文利用高斯函数来描述海杂波多普勒谱,可表示为
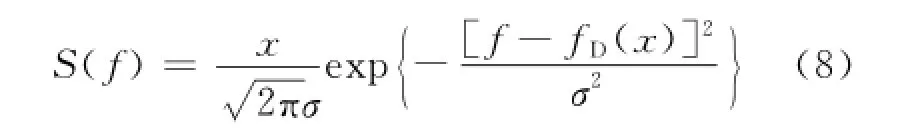
式中:fD(x)为多普勒谱的中心频移,与杂波散射强度x近似线性关系;σ为多普勒谱的谱宽,服从高斯分布。
(3)海杂波的空时相关特性
海杂波距离-时间域上的HRRP协方差矩阵可由其时间相关函数序列和距离相关函数序列的直积生成。HRRP的协方差矩阵为Rs,t,对于Rs,t中的任一元素Rs,t(m,n)有
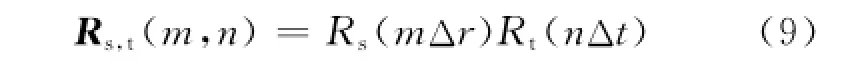
式中:Rs为海杂波HRRP在距离上的相关函数; Δr为海杂波HRRP序列中单个距离单元的长度;Rt为海杂波HRRP在时间上的相关函数,为单个距离单元内海杂波强度的时间相关函数的平均;Δt为雷达的脉冲重复间隔。
海杂波HRRP的距离相关函数Rs由式(6)给出,海杂波HRRP的时间相关函数Rt也可由指数衰减函数来描述为
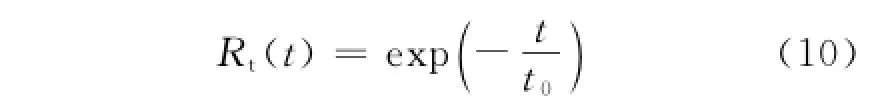
式中:t0为海杂波幅度的平均去相关时间。由IPIX雷达数据分析可知,海杂波纹理分量的相关时间较长,其幅度去相关时间主要由散斑分量决定。较低海况下,散斑分量的相关时间可以达到近百毫秒,而高海况下散斑分量的相关时间可能只有短短十几毫秒[12]。
3 Pareto分布的空时二维相关复海杂波序列生成
(1)空时二维相关海杂波序列的生成模型
依据小擦地角下海杂波的统计分布特性及空间和时间相关特性,本文提出一种时间-距离二维相关的复海杂波生成模型。图2给出该模型的流程图,具体实现步骤:
a)生成海杂波在相邻脉冲下的HRRP,其构成距离-时间域上的二维序列;
b)生成各距离单元中海杂波时间序列的多普勒谱;
c)反演具有给定HRRP和多普勒谱的海杂波的相位信息。
小擦地角下海杂波的幅度可以用Pareto分布模型来描述,对于具有高分辨率和短脉冲间隔的雷达,可以认为其接收到的海杂波在距离和时间上都是相关的。如此,海杂波在相邻脉冲下的HRRP可被认为是一个服从Pareto分布的,在距离-时间域上二维相关的随机序列。另一方面,由相关文献[7-9]给出的结果可知,小擦地角下海杂波在各个距离单元中的多普勒谱中心频率与对应距离单元内海杂波的能量有关,各个距离单元中的多普勒谱相差很大。在对距离-时间域上海杂波序列的多普勒建模时,需要分别考虑各个距离单元内海杂波序列的相关特性。
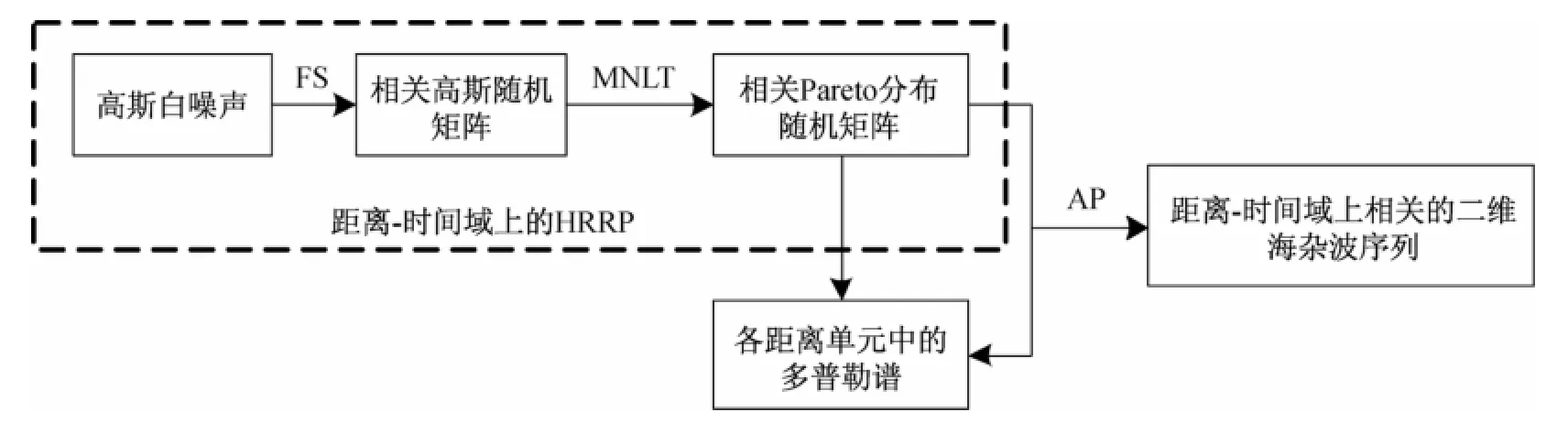
图2 时间-距离二维相关的非高斯复海杂波序列生成模型
(2)海杂波HRRP的生成
由于海杂波在距离-时间域上的HRRP可看作一个距离-时间二维相关并服从Pareto分布的序列,本文采用MNLT方法生成具有指定相关特性的Pareto分布随机序列,并将其视作海杂波在距离-时间域上的HRRP。
MNLT通过对服从标准正态分布的随机序列进行非线性变化,得到具有特定分布函数的非高斯分布随机序列。假设标准正态随机变量x经MNLT得到概率分布函数为Pd(η)的非高斯分布变量η,这两种分布模型需满足关系式[1]:

式中:erfc为余误差函数。
通过解式(11)这个积分方程,可以得到标准正态分布变量x与非高斯分布变量η之间的映射关系为
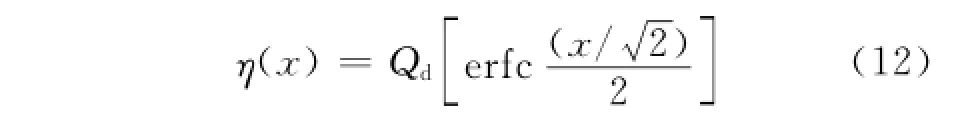
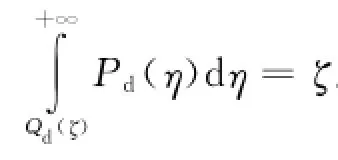

当高斯变量自相关函数为RG(t)时,由式(12)得到的非高斯变量具有相关特性:
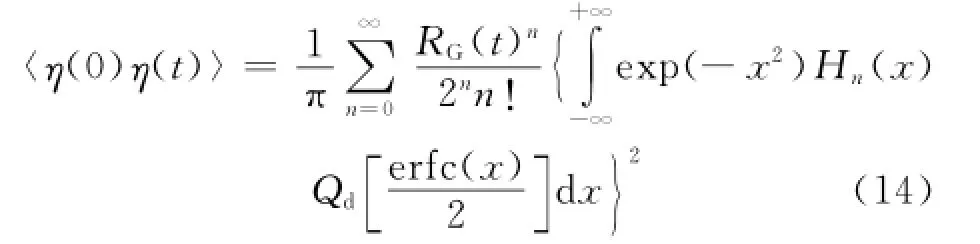
式中:Hn(x)为第n阶Hermite多项式[1]。由式(14)可见,只需通过控制输入高斯随机变量的相关特性,就可利用MNLT得到具有特定相关特性的非高斯分布变量。
图3为不同形状参数下,Pareto分布与复合高斯分布相关特性之间的映射关系。

图3 Pareto分布与高斯分布相关函数的映射关系
(3)相位信息的反演
设某距离分辨单元内的复海杂波时间序列为x(t)=a(t)exp[jθ(t)],其中a(t)为x(t)的幅度序列,θ(t)为x(t)的相位序列。同时,设复海杂波时间序列x(t)的多普勒谱为S0(f)。在已知海杂波幅度信息和多普勒谱后,对海杂波相位信息进行反演实际上是一个优化问题。这个优化问题在数学上可表述为

式中:X(f)为x(t)的频谱;H为所有功率谱为S0(f)的时间序列所构成的集合。
对于这种约束条件和目标函数处在不同域中的优化问题,可以采用AP算法求解[12]。当


4 仿真结果及分析
仿真参数设置:雷达中心频率为9.5 GHz,脉冲重复频率为2 k Hz;雷达发射波形带宽为50 MHz,距离分辨率为3 m;擦地角为6°,雷达视线与风向之间的夹角为30.2°;海面上空风速为7.8 m/s;海杂波幅度的相关距离为17.6 m,相关时间为20 ms。仿真中总共产生125个连续脉冲下的海杂波序列,每个脉冲下海杂波的HRRP中包含512个距离分辨单元,海杂波HRRP的幅度服从形状参数a=2.6,尺寸参数b=0.8的Pareto分布。其中,Pareto分布的参数由对SAXONFPN测量实验中相同条件下得到的实测数据拟合得到[15]。
图4(a)为仿真中得到的距离-时间域上,最大值归一化的海杂波HRRP,其中海杂波HRRP的单位为dB。图4(b)对比了海杂波HRRP幅度理论和仿真中的CDF。图5(a)为海杂波HRRP理论上的协方差矩阵,图5(b)为仿真中,经MNLT得到的距离-时间二维相关的海杂波序列的协方差矩阵。观察图4和图5可知,利用MNLT方法得到的海杂波HRRP其统计和相关特性均与理论结果吻合得很好。
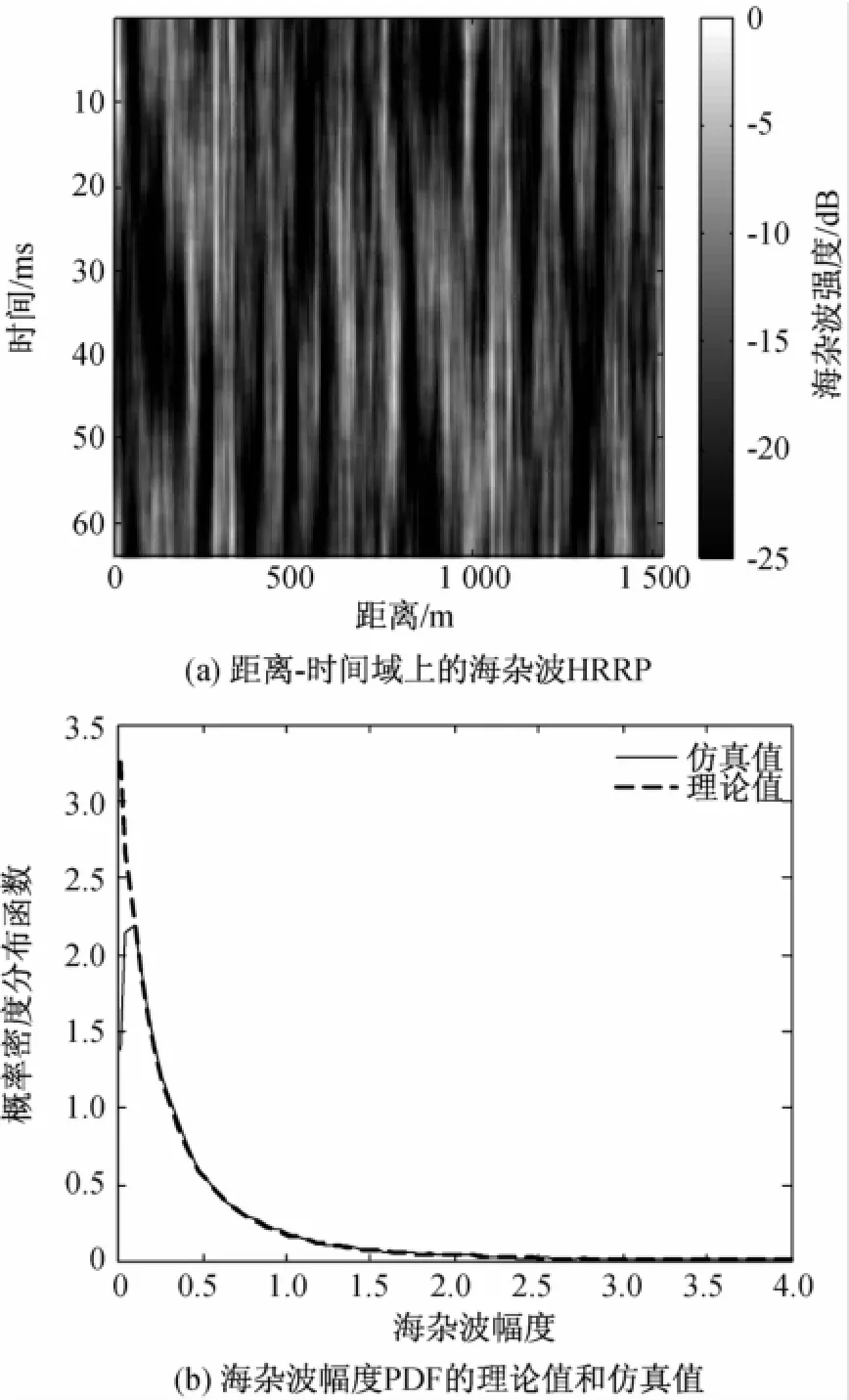
图4 仿真得到的海杂波HRRP及其幅度统计特性
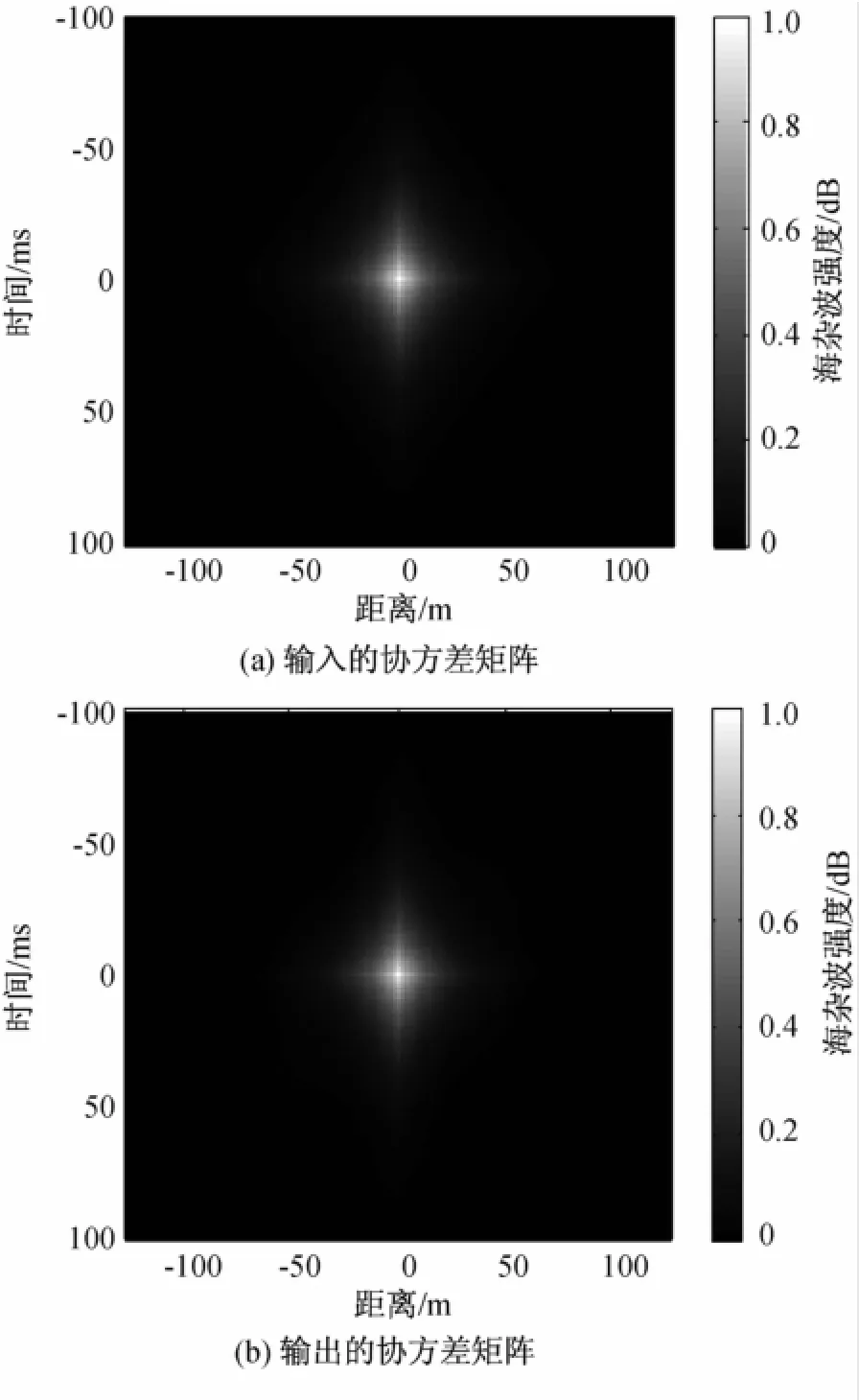
图5 时间空间相关的海杂波HRRP在距离-时间域上的协方差矩阵
获得海杂波在距离-时间域中的HRRP后,利用多普勒模型仿真生成海杂波在各个距离分辨单元中的多普勒谱。图6(a)给出了当海杂波HRRP如图4(a)所示时,理论上海杂波的距离-多普勒谱。图6(a)中截取多普勒频率范围为―500 Hz~500 Hz,多普勒中心频率的均值与相同条件下SAX-FPN测量实验中海杂波的多普勒中心频率相同[15],为52.54 Hz。图6(b)为利用AP算法反演相位信息后,最终得到的复海杂波序列的距离-多普勒谱。相位信息反演过程中,设定AP算法的输出门限为0.02,其平均迭代步数为36.58。仿真输出的海杂波距离-多普勒谱的中心频率均值为51.85 Hz,与期望的海杂波多普勒中心频率的均值相差不到1 Hz,十分接近。对比图6(a)和图6(b)可见,仿真输出的海杂波序列的距离-多普勒谱与期望得到的海杂波距离-多普勒谱的形状及多普勒峰值频率等主要特征十分相似,这表明在海杂波幅度信息确定时,AP方法能够准确反演海杂波的相位信息,从而得到具有特定幅度信息和相关特性的海杂波序列。图7为X波段、4~5级海况下实测海杂波数据的距离-多普勒谱[14]。将图7与图6(b)对比可见,本文仿真得到的距离-多普勒谱与实测数据十分类似,不同距离单元下海杂波多普勒谱的中心频率和谱宽均存在差异,表明了本文仿真结果的有效性。
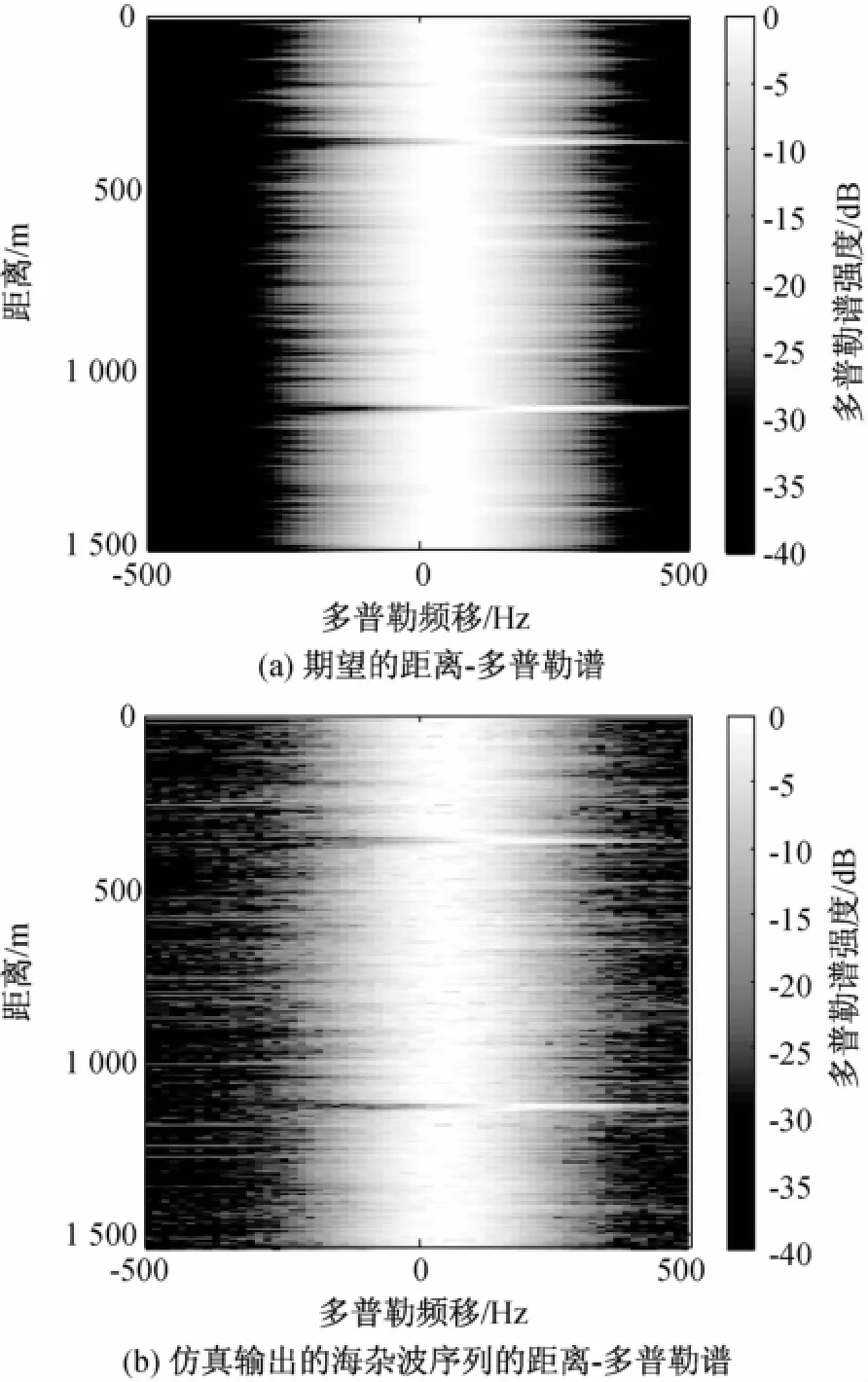
图6 海杂波序列的距离-多普勒谱的理论值和输出值

图7 实测海杂波序列的距离-多普勒谱
5 结论
基于小擦地角下海杂波的统计分布特性和距离时间相关特性,本文提出了一种空时二维相关的海杂波生成模型。该模型首先利用MNLT生成了二维Pareto分布随机矩阵,视其为由各脉冲下海杂波HRRP构成的矩阵;随后,依据海杂波各个距离分辨单元中多普勒特性与HRRP的对应关系,生成各个距离分辨单元中的多普勒谱;最终并利用交替投影(AP)算法反演出具有确定HRRP和多普勒谱的海杂波复散射信号的相位信息,从而得到具有给定统计特性和空间时间二维相关特性的复海杂波序列。仿真结果表明,该模型生成的海杂波在功率统计特性上服从Pareto分布,其概率密度分布函数具有海尖峰带来的长拖尾现象;在距离和时间上二维相关,不同距离单元内的时间相关特性各不相同,并与对应距离单元内的杂波幅度有关。
[1]K.D.Ward,R.J.A.Tough,S.Watts.Sea Clutter:Scattering,the K Distribution and Radar Performance[M].London:the Institution of Engineering and Technology,2006.
[2]K.D.Ward.Compound Representation of High Resolution Sea Clutter[J].Electronic Letters, 1981,17:561-565.
[3]许小剑,李晓飞,刁桂杰,等.时变海面雷达目标散射现象学模型[M].北京:国防工业出版社,2013.
[4]Y.Dong.Distribution of X-band High Resolution and High Grazing Angle Sea Clutter[R].DSTORR-0316,DSTO,2006.
[5]D.R.Thompson.The Pareto Distribution for Low Grazing Angle and High Resolution X-band Sea Clutter[C].IEEE Radar Conference,2010: 789-793.
[6]S.Bocquet.Simulation of Correlated Pareto Distributed Sea Clutter[C].IEEE Radar Conference, 2013:253-258.
[7]C.S.Chae,J.T.Johnson.A Study of Sea Surface Range-resolved Doppler Spectra Using Numerically Simulated Low-grazing-angle Backscatter Data[J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(6):3452-3460.
[8]J.T.Johnson,R.J.Berkholder,J.V.Toporkov,et al.A Numerical Study of Retrieval Sea Surface Height Profiles from Low-grazing Angle Radar Data[J].IEEE Transactions on Geoscience and Remote Sensing,2009,47(6):1641-1650.
[9]M.A.Rtchie,A.G.Stove,S.Watts,et al. Application of a New Sea Clutter Doppler Model[C].IEEE Radar Conference,2013:560-565.
[10]M.Farshchian,F.L.Posner.The Pareto Distribution for Low Grazing Angle and High Resolution X-band Sea Clutter[C].IEEE Radar Conference, 2010:789-793.
[11]S.Watts.Cell-averaging CFAR Gain in Spatially Correlated K-distribution[J].IEE Proceedings Radar Sonar and Navigation,1996,143(5):321-327.
[12]刘裕.海杂波特性分析与仿真[D].西安:西安电子科技大学,2011.
[13]L.K.Patton.On the Satisfaction of Modulus and Ambiguity Function Constraints in Radar Waveform Optimization of Detection[D].Wright State University,2009.
[14]S.Bocquet,L.Rosenberg,S.Watts.Simulation of Coherent Sea Clutter with Inverse Texture[C]. IEEE Radar Conference,2014.
[15]B.L.Gotwols,R.D.Chapman,D.R.Thompson.Doppler Spectra and Backscatter Cross Section over 45°~85°Incidence[C].NATO-RTO Symposium,2000.
A Model for Spatially and Temporally Correlated Low Grazing Angle Sea Clutter Simulation
WANG Jia-ning, XU Xiao-jian
(Beihang University,Beijing 100191,China)
This paper proposes a model for simulation of the temporally and spatially correlated low grazing angle sea clutter based on the statistical and correlated characteristics. Firstly,the memoryless nonlinear transform(MNLT)is adopted to directly simulate the Pareto distributed high resolution range profiles(HRRPs)of the temporally and spatially correlated sea clutter from coherent pulses.Secondly,by utilizing the approximately linear relationship between the Doppler central frequency and HRRP range Doppler spectrum of each range bin is modeled.Then,the alternating projection(AP)approach is used to retrieve phases of sea clutter with the desired Doppler spectrum and the given magnitudes.Simulation results show that the proposed model can generate the Pareto distributed temporally and spatially correlated sea clutter with desired spatial correlation function and range resolved Doppler spectra.
spatially and temporally correlated;small grazing angle;Pareto distribution; Doppler spectrum;sea clutter
TN011
A
1671-0576(2014)04-0007-07
2014-09-15
王佳宁(1988―),女,博士研究生,主要从事海面电磁散射特性计算、分析、海杂波建模等研究;许小剑(1963―),男,教授,博士,主要从事遥感特征建模、分析与处理、雷达成像与目标识别、智能化信息处理等研究。

