一种Gaussian-Hermite矩分块重构的抗几何攻击水印算法
贾晓琳,葛建超,綦艳丽,邵利平
(1.西安交通大学电子与信息工程学院, 710049, 西安; 2.陕西师范大学计算机科学学院, 710062, 西安)
一种Gaussian-Hermite矩分块重构的抗几何攻击水印算法
贾晓琳1,葛建超1,綦艳丽1,邵利平2
(1.西安交通大学电子与信息工程学院, 710049, 西安; 2.陕西师范大学计算机科学学院, 710062, 西安)
针对目前抗几何攻击水印算法易在大尺度几何攻击下失效的问题,提出了一种基于几何校正和分块重构的局部区域水印算法,从而提高水印的鲁棒性和提取精度。该算法利用图像不变质心进行几何形变参数的估计,对图像进行几何校正以实现载体的同步;根据几何攻击对图像视觉质量影响的分析,筛选可嵌入分块;利用高斯-埃尔米特矩良好的图像重构能力,修改特定矩集,实现水印嵌入,获得含水印图像。为验证算法的抗几何攻击能力,对含水印载体图像遭受旋转、缩放、平移和其他常规性攻击后的性能进行了实验测试。实验结果表明,所提算法可抵抗多种几何攻击及常规图像攻击,能提取出较高精度的水印信息,相对于其他算法,水印的鲁棒性虽然相差无几但在保持较高视觉不可见性的前提下,嵌入容量有了一定程度的提高。
数字水印;几何攻击;不变质心;高斯-埃尔米特矩
由于矩函数良好的图片特征表达能力,矩理论在模式识别、图像处理中的应用日益广泛。HU矩[1]因其简明的几何意义,最先被引入图像领域,然而由于不具备正交性,HU矩计算中的信息冗余不可避免。针对该问题,Teague等引入了正交矩的概念[2],首次将Zernike矩和Legendre矩应用于图像分析领域。基于此,文献[3]结合哈希算法和Zernike矩的旋转不变性,实现了算法对旋转攻击的鲁棒性;Kim等结合图像归一化与Zernike矩的旋转不变性,实现水印的抗几何攻击能力[4],并通过调整水印的嵌入强度保证含水印图像具有良好的视觉不可见性。
由于连续矩在应用于数字图像时须进行离散化,离散误差难以避免。Mukundan等首次采用基于离散正交函数的Tchebichef矩来对图像进行分析[5]。在此基础上,张力等利用原始图像的Tchebichef矩估计几何形变参数[6],在提取水印前进行相应逆变换,提高了算法的抗几何攻击能力和水印提取精度;Yap等利用Tchebichef矩的图像重构能力,以扩频方式构造水印[7],直接对矩的修改实现水印的嵌入,但该算法对几何攻击不具有鲁棒性。
Gaussian-Hermite矩(GH矩)[8]是Shen等提出的,已有学者将其应用于运动物体检测、虹膜以及指纹识别等领域,而在水印领域的研究还相当有限。GH矩尽管是连续矩,但其在图像重构方面的性能优越,对旋转和平移攻击也具有较强的稳定性。因此,本文将其应用于抗几何攻击水印算法的实现。
1 GH矩及其性质
文献[9]指出,GH矩是以GH多项式为基函数的矩集,给定一幅定义在ζ上的密度函数为f(x,y)的图像,其(p,q)阶高斯-埃米尔特矩定义为
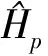
(1)
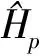
(2)
GH多项式在区间(-∞,+∞)上是连续正交的,应用于数字图像时,需首先进行离散化。假设数字图像的密度函数为I(i,j),定义在[0≤i,j≤K-1]区间上,图像坐标系的归一化表示为
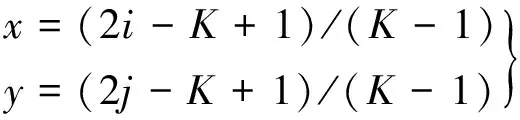
(3)
由此可将式(1)中的GH多项式转化成离散形式
(4)
此时图像的离散GH矩计算如下
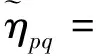
(5)
通过图像重构实验得知,GH矩重构图像的视觉质量基本可以满足水印的嵌入要求,可考虑通过修改GH矩来进行水印嵌入。
考虑到矩计算的相关性以及不同阶矩修改对图像重构质量的影响,应筛选那些矩值修改对其他矩影响较小,且不会造成图像严重降质的矩作为水印嵌入的模板。
当矩的修改数目较少时,重构图像计算所得的对应修改矩的幅度变化最为明显;当修改数目较多时,影响会相互累加,使得未修改矩的波动幅度变大。不同的修改策略会造成图像质量的巨大差异。
2 几何校正及可嵌入分块提取
2.1 基于不变质心的几何校正
所谓不变质心,指的是经历一系列图像处理,例如图像旋转、缩放、平移以及压缩、去噪等操作后仍保持原始图像中相对位置不变的像素点。
基于不变质心的几何校正就是在原始图像中提取多个不同半径下的不变质心,记录相关数据,提取攻击后图像对应半径的不变质心点,实现几何形变参数估计,并进行对应的逆变换以实现载体同步。
不变质心的提取步骤如下。在水印嵌入端有3个步骤。
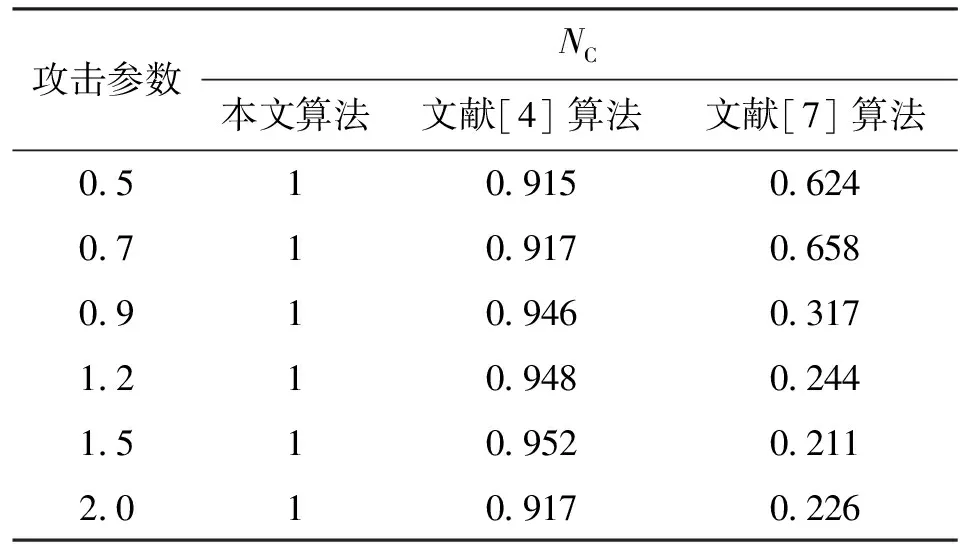
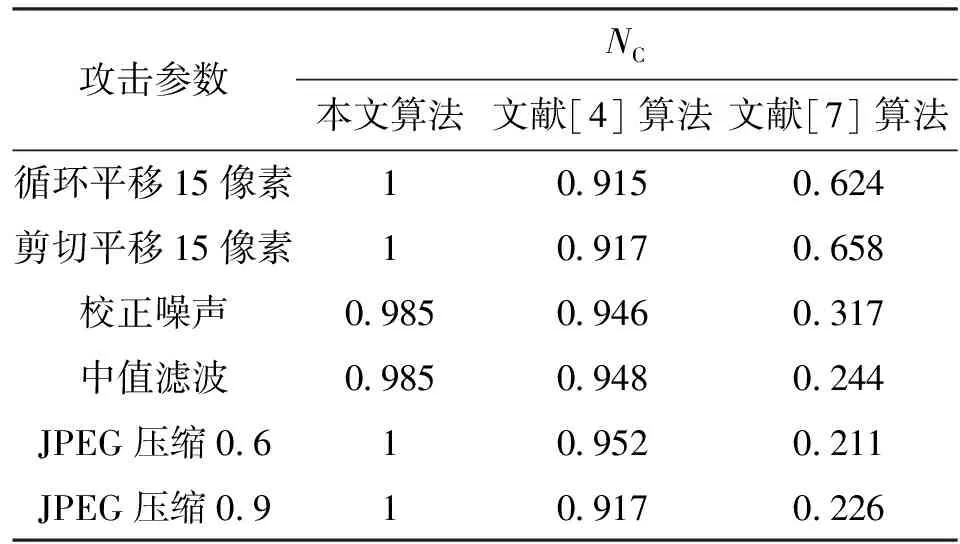
步骤1在原始图像(含水印图像,大小为M×M)中,以图像中心作为首个不变质心迭代初始点,选取迭代半径R(例如M/2),此时R应尽可能大。每次求取区域质心后,比较迭代半径R与该质心到图像边界的最小距离Rd,若R 步骤2取圆心C1、半径R1区域内的像素,填充背景像素生成2R1×2R1大小的新图像。 步骤3在新图像中,以C1为迭代初始点,半径为R=R1-ΔR,再次迭代提取两个不变质心,并记录各自的坐标及对应迭代半径。在提取过程中若出现3个不变质心位于同一直线上的情况,则继续缩小迭代半径求非线性相关的3个不变质心点。至此,获得3组记录数据(C1,R1)、(C2,R2)、(C3,R3)。 在水印提取端有3个步骤。 为提高参数估计的精度,可提取多个不变质心,从中筛选非线性相关且数值具有一定差距的不变质心组进行形变参数的估算。提取多个质心的过程与3个质心的提取过程相同。 (6) 式中:d=x1(y3-y2)+x2(y1-y3)+x3(y2-y1)。 几何形变参数估计可以按照以下方法获得。 (1)旋转角度α的估计伪代码为 (2)缩放参数a、b的估计为 (7) (3)平移攻击参数Δx=a13,Δy=a23。 最后,根据估算的形变参数可进行相应的逆变换来恢复原始图像。 2.2 可嵌入分块提取 从几何攻击对图像视觉影响的分析可知,图像顶点区域易在剪切类几何攻击下发生像素丢失,在水印嵌入前先提取图像的可嵌入分块,以最大程度地避免在几何形变的信息易损区域进行水印嵌入。以256×256的灰度cameraman图像为例,可嵌入分块的具体筛选方法如下。 步骤1对图像进行16×16分块,计算各分块中心到图心的距离,将距离大于L(此处取100)的分块标记为不可嵌入分块。 步骤2对原始图像以canny算子提取图像边缘信息并膨胀化处理,设定筛选阈值m(本文中取20),将剩余分块中包含m个以上边缘像素的分块标记为不可嵌入分块。 步骤3根据标记从原始图像中分离可嵌入分块和不可嵌入分块,获得两幅子图,记为I1、I2;设I1为可嵌入子图,对I1各分块执行水印嵌入,获得含水印图像后与I2叠加,即可获得完整的含水印图像。 图像顶点及边缘区域在几何攻击下容易发生信息损失,不适合作为嵌入模板,应避免在边缘区域进行水印嵌入。文献[10]中的部分操作是利用灰度图像的梯度信息进行边缘提取,获得图像的边缘信息,并采用线性函数对提取的边缘线进行膨胀化以获取连续的边缘线。 3.1 算法基本思路 在几何攻击和一般常规图像处理下,图像不变质心有良好的稳定性,利用形变前后对应点的位置变化可计算相应的形变参数,且具有一定的准确度。以此为基础,拟选取稳定的不变质心组进行几何形变参数估计并进行校正,实现算法的抗几何攻击能力。同时,根据GH矩在图像重构方面的优异表现,可通过修改矩集图像重构来实现水印的嵌入和提取。 3.2 算法具体实现 水印算法的具体实现包括水印的嵌入和提取两部分。设原始图像为M×N大小的灰度图像I(i,j),水印W(i)是长度为L1的二值序列。具体操作步骤如下。 (1)水印嵌入方法如下。 步骤1对图像I(i,j)进行低通滤波以提高算法对常规图像处理的鲁棒性。 步骤2提取图像的不变质心族,并记录相关数据(C1,R1/M)、(C2,R2/M)、(C3,R3/M),详细的提取方法参见2.1节。 步骤3对图像进行边缘提取及膨胀化处理,获取连续的边缘图像。 步骤4对边缘图像进行16×16分块操作,分离不可嵌入分块和可嵌入分块,获得可嵌入子图I1(i,j)和不可嵌入子图I2(i,j)。 步骤5计算I1(i,j)各分块的GH矩,选择并记录修改的矩集为key,根据水印信息对集合中的矩修改为 (8) 式中:τ为矩修改强度。 以上水印嵌入过程中使用的几何校正的必要信息、分块提取信息(L,m)、修改的矩集key、矩修改强度τ及图像I1(i,j),将作为水印提取的必要信息。 需要注意的是,在选取矩集时,应根据第1节GH矩的性质,选择修改矩的变化幅度较大,而对其余矩影响较小的矩集作为嵌入载体。记录可嵌入矩集,作为提取水印的必要数据。 (2)水印提取。水印提取端的检测图像为I′(i,j),图像大小记为M′×N′,水印提取方法如下。 步骤1首先对待提取水印的图像I′(i,j) 进行低通滤波处理。 (9) 3.3 实验结果与分析 在AMD速龙双核5000+台式机、主频2.81 GHz、内存4 GB、eclipse-SDK-3.2平台上进行验证性实验。实验中选择256×256的cameraman图像(见图1a)作为载体图像,随机产生一个64位的二值序列作为嵌入水印。为简单起见,本文只对各可嵌入分块的(2,0)阶矩进行嵌入。如实际使用过程中需嵌入多于64位的水印信息,可根据嵌入需要进一步筛选测试可嵌入矩。几何校正的提取数据采用[44,40,32],精度ε取0.0001,τ取为0.05,L=100,m=20,含水印图像如图1b所示,其峰值信噪比PSNR为42.24 dB。 图1 原始图像与含水印图像 为验证算法的抗几何攻击能力,本文对水印在包括旋转(剪切类和非剪切类)、缩放和平移(剪切类和循环类)的各类攻击下的性能进行了测试,并与Kim等提出的基于Zernike矩的水印算法[4]以及Yap等提出的基于Tchebichef矩的水印算法[7]进行比较,对各算法产生的水印图像的图像质量进行了对比分析。表1列出了本文算法与文献[4,7]算法受到两类旋转攻击后提取水印与原水印的NC。 由表1、表2可知,本文算法能够抵抗任意角度,甚至包括带剪切的旋转攻击,且水印提取精度较高,这主要是因为采用了几何参数估计校正以及易损区域规避策略。文献[4]算法利用Zernike矩本身的旋转不变性,实现了对旋转攻击的鲁棒性,但随着攻击角度的增加,水印的提取精度稍有降低。文献[7]算法不具有抗旋转攻击的能力。表3给出了缩放攻击下提取水印的NC对照情况。 表1 本文算法与文献[4,7]算法在非剪切旋转攻击后提取水印与原水印的相似度比较 表2 本文算法与文献[4,7]算法在剪切旋转攻击后提取水印与原水印的相似度比较 表3 本文算法与文献[4,7]算法在缩放攻击后提取水印与原水印的相似度比较 攻击参数NC本文算法文献[4]算法文献[7]算法0 510 9150 6240 710 9170 6580 910 9460 3171 210 9480 2441 510 9520 2112 010 9170 226 从表3中的NC对照情况可看出,由于采用了缩放参数估计,本文算法能够实现对应尺寸的逆变换,且保持较高的水印提取精度。由于缩放攻击下插值操作的发生频度高于旋转变换,像素整体变化程度较大,水印的提取精度略有降低。Kim等采用归一化处理,实现攻击前后尺寸归一,对缩放攻击有较好的鲁棒性。表4给出了平移及常规攻击下的对比情况。就图像质量而言,本文算法的PSNR为42.24 dB,文献[4]算法含水印图像的PSNR为48.06dB,而文献[7]算法PSNR为32.98 dB。 通过以上实验数据可以看出,在对含水印的载体图像进行旋转、缩放、平移和其他鲁棒性攻击后,本文算法仍能提取出较高精度的水印信息,相对于文献[4]算法,各项攻击下水印的鲁棒性虽然相差无几,但在保持较高视觉不可见性的前提下,嵌入容量有了一定程度的提高。虽然距离文献[7]算法嵌入容量仍有很大差距,但本文算法通过图像校正,实现了水印的抗几何攻击能力,并改善了图像的视觉质量,同时克服了多数算法不能抵抗剪切类攻击的缺点,且提取的水印始终能保持较高的精度。 表4 本文算法与文献[4,7]算法在其他攻击后提取水印与原水印的相似度比较 攻击参数NC本文算法文献[4]算法文献[7]算法循环平移15像素10 9150 624剪切平移15像素10 9170 658校正噪声0 9850 9460 317中值滤波0 9850 9480 244JPEG压缩0 610 9520 211JPEG压缩0 910 9170 226 算法利用不变质心的几何稳定性估计几何形变参数,对图像进行逆变换实现攻击前后的载体同步;引入边缘提取对图像易损区域进行分块标记,实现了最大程度地避免在信息损失区域嵌入水印;最后利用GH矩良好的重构性能,通过筛选和修改可嵌入分块的特定矩集进行水印嵌入,获得了含水印图像。实验结果表明,所提水印算法具有对几何攻击和常规攻击的鲁棒性,能保持较高的水印提取精度,并且能够抵抗一定尺度的剪切类几何攻击。 [1] HU Ming-Kuei.Visual pattern recognition by moment invariants [J].IRE Transactions on Information Theory, 1962, 8(2): 179-187. [2] TEAGUE M R.Image analysis via the general theory of moments [J].Optical Society of America, 1980, 70(8): 920-930. [3] SUN Rui, YAN Xiaoxing, ZENG Wenjun, et al.Geometric invariant robust image hashing via Zernike moment [J].International Journal of Wireless and Microwave Technologies, 2011, 1(5): 9-15. [4] KIM H S, LEE H K.Invariant image watermark using Zernike moments [J].IEEE Transactions on Circuits and Systems for Video Technology, 2003, 13(8): 766-775. [5] ALGHONIEMY M, TEWFIK A H.Geometric distortion correction through image normalization [C]∥Proceedings of the IEEE International Conference on Multimedia and Expo.Piscataway, NJ, USA: IEEE, 2000: 1291-1294. [6] 张力, 韦岗, 张基宏.Tchebichef 矩在图像数字水印技术中的应用 [J].通信学报, 2003, 24(9): 10-18. ZHANG Li, WEI Gang, ZHANG Jihong.Application of Tchebichef moment in image watermarking techniques[J].Journal of China Institute of Communications, 2003, 24(9): 10-18. [7] YAP P T, PARAMESRAN R.An image watermarking scheme based on orthogonal moments [C]∥Proceedings of the IEEE Region 10Annual International Conference.Piscataway, NJ, USA: IEEE, 2005: 1-4. [8] SHEN Jun.Orthogonal Gaussian-Hermite moments for image characterization [C]∥Proceedings of the Intelligent Robots and Computer Vision: XVI Algorithms, Techniques, Active Vision, and Materials Handling.Pittsburgh, PA, USA: SPIE, 1997: 875-894. [9] YANG Bo, DAI Mo.Image analysis by Gaussian-Hermite moments [J].Signal Processing, 2011, 91(10): 2290-2303. [10]JIA Xiaolin, QI Yanli, SHAO Liping, et al.A watermark algorithm based on SVD and image geometric correction [C]∥Proceedings of the IEEE International Conference on Systems and Informatics.Piscataway, NJ, USA: IEEE, 2012: 1861-1865. (编辑 武红江) Anti-GeometricDigitalWatermarkAlgorithmwithBlockReconstructionofGaussian-HermiteMoments JIA Xiaolin1,GE Jianchao1,QI Yanli1,SHAO Liping2 (1.School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2.School of Computer Science, Shaanxi Normal University, Xi’an 710062, China) A novel local watermarking algorithm with geometric correction and block reconstruction is proposed to deal with losing effectiveness in resisting large scale geometric attacks.The robustness and extraction precision of watermarking can be improved by this algorithm.Image invariant centroid is extracted to estimate geometric deformation parameters, and then the corresponding geometric correction is performed to achieve the carrier synchronization.The embeddable blocks are selected by analyzing the geometric attack influences to the image visual quality.Taking advantage of the excellent image reconstruction ability of Gaussian-Hermite moments, specially designated block moment collection is modified to embed watermarks.The experiments show that the proposed algorithm with good visual invisibility enables to resist various geometric attacks and common image processing impacts. digital watermarking; geometric attack; invariant centroid; Gaussian-Hermite moment 2013-10-17。 贾晓琳(1963—),女,讲师。 国家自然科学基金资助项目(61100239;60803088);陕西省科技新星资助项目(2011kjxx17);陕西省自然科学基金资助项目(2011JQ8009);教育部高等学校博士学科点专项科研基金资助项目(20100201110063)。 时间:2014-01-16 10.7652/xjtuxb201404004 TP393 :A :0253-987X(2014)04-0020-06 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140116.1658.004.html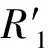
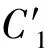
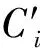
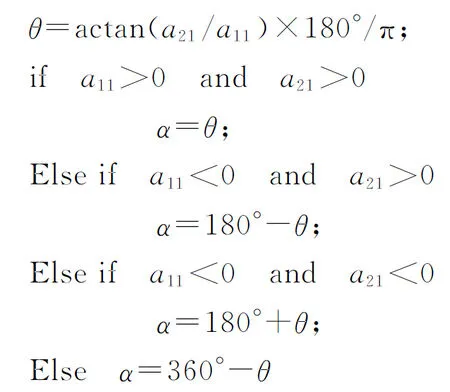
3 基于局部几何校正和图像分块重构的水印算法
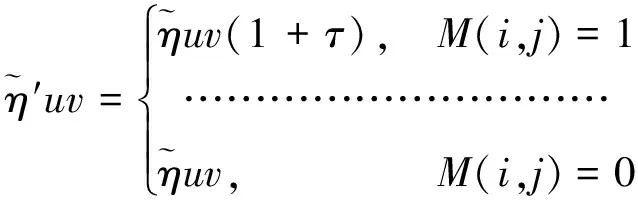
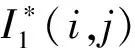
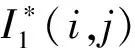
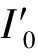
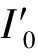
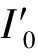
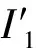



4 结 论

