多扩展目标的高斯混合概率假设密度滤波器

韩玉兰,朱洪艳,韩崇昭,王静

(1.西安交通大学电子与信息工程学院, 710049, 西安; 2.西安邮电大学电子工程学院, 710121, 西安)

多扩展目标的高斯混合概率假设密度滤波器

韩玉兰1,朱洪艳1,韩崇昭1,王静2

(1.西安交通大学电子与信息工程学院, 710049, 西安; 2.西安邮电大学电子工程学院, 710121, 西安)

针对多扩展目标跟踪中状态信息难以估计的问题,提出了一种可以估计扩展目标运动状态和形状信息的多扩展目标高斯混合概率假设密度(RHM-GMPHD)滤波器。首先利用描述凸星形扩展目标量测源分布的随机超曲面模型和传感器量测方程,建立扩展目标运动状态及形状信息与量测之间关系的伪量测函数;然后结合扩展目标状态预报信息,推导了扩展目标状态更新方程,递推地对扩展目标运动状态及形状信息进行估计跟踪。此外,还建立了Jaccard距离来度量RHM-GMPHD滤波器对目标形状的估计性能。与联合概率数据关联(JPDA)滤波器和GMPHD滤波器相比,RHM-GMPHD滤波器不仅可以估计凸星形扩展目标的形状信息,并能有效提高对目标数和运动状态的估计精度。仿真实验表明,RHM-GMPHD滤波器对质心估计的均方根误差分别约为JPDA和GMPHD滤波器的1/3和1/2,对目标数的估计接近真实值,对形状估计的Jaccard距离一般小于0.2。

扩展目标跟踪;高斯混合概率假设密度;随机超曲面模型;形状估计

扩展目标跟踪在近距离跟踪(如濒海监视、自主式武器、机器人技术)中非常重要[1]。另外,群目标跟踪在多目标编队、地面空中或海面目标群、人群或兽群跟踪等领域有巨大的应用价值。通常群内目标比较密集,对群目标内所有个体进行跟踪是不现实的也不必要[2],但可直接对群的整体进行跟踪。由于扩展目标和群目标跟踪的数学描述类似,许多文献将扩展目标与群目标放在一起进行研究[1,3-6],也有文献将群目标直接称为扩展目标[1,4-5]。

扩展目标和群目标跟踪在近十几年受到了国内外学者的广泛关注。文献[1,3]将目标形状参数用半正定随机矩阵描述,采用贝叶斯递推的方法,对单个扩展目标或群目标的运动状态和形状跟踪,这种方法被称为随机矩阵法。文献[4-5]提出采用随机超曲面模型来描述量测源在物体表面的分布,对单个扩展目标进行估计与跟踪。多扩展目标或群目标的跟踪方法有2类:一类是将单个扩展目标的跟踪方法与概率多假设跟踪(PMHT)相结合[6-7]实现多扩展目标的跟踪,由于其数据关联的计算量比点目标繁重得多,并且随着扩展目标个数及量测数急剧增加,因此应用范围受到限制;另一类是基于随机有限集,这类方法递推地传递目标状态的分布信息,不需要数据关联即可从目标状态分布中同时提取目标的个数和状态估计[8-10],但这类算法只对扩展目标运动状态进行估计,没有考虑形状。文献[11]将随机矩阵法[1]与扩展目标高斯混合概率假设密度滤波器[10]相结合,对扩展目标的运动状态和形状进行估计,但其将所有目标都近似为椭圆,形状估计误差较大,影响进一步决策的正确性。

针对扩展目标形状不规则时难于对形状估计的问题,本文提出了一种基于随机超曲面的扩展目标高斯混合概率假设密度(RHM-GMPHD)滤波器,可以在杂波和漏检测情况下跟踪任意凸星形目标的运动状态和形状。本文为了更新扩展目标的状态,建立了扩展目标的伪量测和量测似然函数,并在合理的假设和近似下,推导了扩展目标运动状态和形状参数的量测更新方程,建立了度量滤波器对不规则形状估计的性能指标。

1 问题描述

扩展目标状态由目标的运动状态参数和形状参数组成,k时刻的扩展目标状态集可表示为

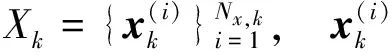
(1)

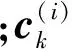
本文的研究基于下述假设。

假设1每个目标状态演化服从线性高斯运动模型,但各目标之间演化互不相关。第i个目标的状态演化模型可表示为

(2)

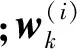
假设2量测方程亦服从线性高斯模型,目标产生的量测之间互不相关。

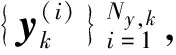
(3)

假设3测量集由源于目标的量测和杂波构成,杂波与目标产生的量测之间互不相关,目标产生的量测数和杂波量测数均服从泊松分布。

2 扩展目标高斯混合PHD滤波器

2.1 随机超曲面模型

随机超曲面模型是描述扩展目标量测源分布的模型[4],可描述如下。

(4)

图1 随机超曲面模型产生量测源示意图

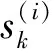
2.2 伪量测函数

集合E⊂RN中的任何一点到质心的线段记为g,若g上所有点仍属于此集合,则称集合E形成的形状为凸星形[5]。

下面的讨论局限在二维空间,高维空间很容易扩展。由式(4)的随机超曲面模型和径向函数[12]r(φ)对凸星形进行表示

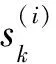
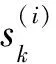
(5)

式中:η(φ)=[cos(φ),sin(φ)]T为角度φ的单位向量;径向函数r(φ)可由Fourier系数描述

(6)

对于固定角度φ,式(6)可用向量表示

r(φ)=r(φ)lk

(7)

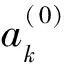
由式(3)和式(5)可得量测方程

(8)

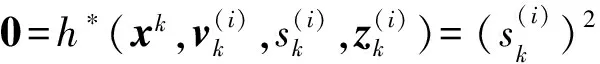
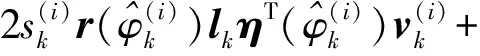
(9)

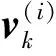
2.3RHM-GMPHD滤波器的递推

RHM-GMPHD滤波器基于以下假设[13]:

假设4预测目标数服从Poisson分布;

假设5生存概率和检测概率与目标状态无关;

假设6目标的新生和衍生强度为高斯混合。

对于多扩展目标跟踪,其预测方程与标准高斯混合PHD[13]的预测方程相同,因此这里只介绍量测更新方程。

扩展目标PHD的后验强度为PHD的预测强度υk|k-1(x|Z)与量测伪似然函数LZk的乘积[8]

υk|k(x|Z)=LZk(x)υk|k-1(x|Z)

(10)

PHD的预测强度具有如下高斯混合形式

(11)

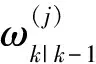
LZk(x)=1-(1-e-γ(x))pD(x)+

(12)

式中:ζ|→Zk表示划分ζ将量测集Zk分割为非零胞;ωζ为划分ζ的权值;dW为胞W的非零权值系数;pD(·)为检测概率;γ(·)为扩展目标产生量测个数的均值;φz(·)=fL(z|·)为量测z的似然函数;λk为单位空间的杂波数;ck(·)为杂波分布函数。

将式(11)、(12)代入式(10)得

(13)

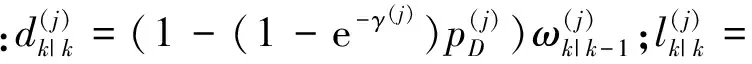
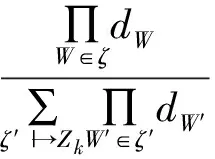
(14)

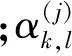
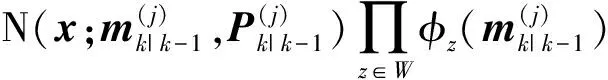
(15)

式中:fL(zk,l|xk) 为量测zk,l的似然函数。

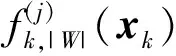
(16)

3 扩展目标形状估计的性能指标

本文借鉴了Jaccard系数[14]的思想,建立了几何形状间的Jaccard距离,将其作为对扩展目标形状估计的性能指标。本文定义几何形状X与Y之间的Jaccard距离为

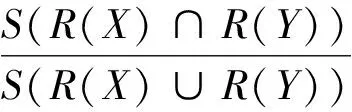
(17)

式中:R(X)、R(Y)表示由几何形状X、Y所形成的区域;S(·)表示区域的面积;DJac的取值范围为[0,1]。Jaccard距离体现了2个几何形状的大小、位置、方向共同作用下的差异。本文首先将估计形状的质心移到实际质心位置,再采用Jaccard距离对形状的估计性能进行度量。

可以证明,Jaccard距离符合度量的条件。

(1)正定性:DJac(X,Y)≥0,当且仅当X=Y时等号成立。

(2)对称性:DJac(X,Y)=DJac(Y,X)。

(3)三角不等式

DJac(X,Z)≤DJac(X,Y)+DJac(Y,Z)

(18)

显然条件(1)、(2)成立,下面对条件(3)进行证明。

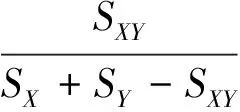
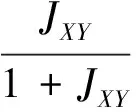
(19)

由几何形状的并交关系,下列不等式成立

SY-SYZ-SXY+SXZ≥0

(20)

SX≥SXY;SZ≥SYZ

(21)

将式(19)的关系应用到式(20),可得

(22)

将式(19)应用到式(21),可得

SX≥JXYSY;SZ≥JYZSY

(23)

由式(17)可知,当JXY≤JXZ或JYZ≤JXZ时,DXY≥DXZ或DYZ≥DXZ成立,因此式(18)成立。

当JXY≥JXZ且JYZ≥JXZ时,由式(23)得

(24)

(25)

由式(22)、(24)、(25)整理得

1+JXZ≥JXY+JYZ

(26)

再由式(17),可证式(18)成立。

4 仿真结果

4.1 仿真场景设置

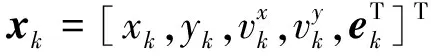
扩展目标的生存概率和检测概率均为0.99。杂波量测数目服从均值为10的泊松分布,在监测区域均匀分布。每个目标在每一时刻产生量测的个数服从均值为20的泊松分布。设置新生强度为

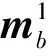
(27)

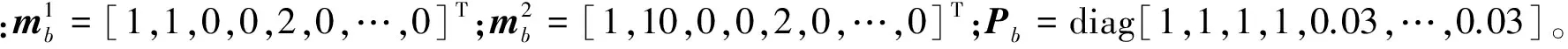
设置衍生强度为

υβ(x)=0.05N(x;ξ,Pβ)

(28)

式中:Pβ=diag[1,…,1];ξ为衍生出新目标的本体目标的状态向量。目标的主轴方向与运动方向一致。

4.2 凸星形扩展目标的跟踪

采用RHM-GMPHD、JPDA和GMPHD滤波器对形状如图2所示的3个凸星形扩展目标进行跟踪,目标航迹如图3所示。目标1、2的生存周期为1～30s,大约16s时两目标相交,目标3的生存周期为21～30s。形状参数先验函数设置为均值[2,0,…,0]T、方差为diag[0.03,…,0.03]的高斯函数。为得到JPDA、GMPHD和RHM-GMPHD滤波器在质心位置、数目及形状方面的估计性能,本文进行了100次Monte Carlo仿真实验,结果如图4～6所示。

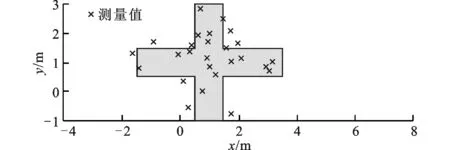
图2 凸星形扩展目标的形状

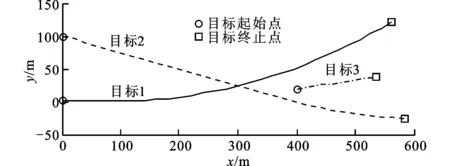
图3 目标运动轨迹

图4给出了本文RHM-GMPHD滤波器、针对多点目标的JPDA滤波器,以及针对点目标的GMPHD滤波器的位置均方根误差曲线。由图4可以看出,RHM-GMPHD滤波器在质心估计方面的跟踪性能,明显优于将扩展目标当做点目标的JPDA和GMPHD滤波器。由于JPDA滤波器不能自适应地估计目标数,因此在估计过程中设置目标数已知,图5给出了RHM-GMPHD和GMPHD滤波器的目标估计数。由于GMPHD将扩展目标当做点目标,因此目标数估计出现严重偏差,而RHM-GMPHD滤波器只有在两目标的距离较近时出现一些偏差。

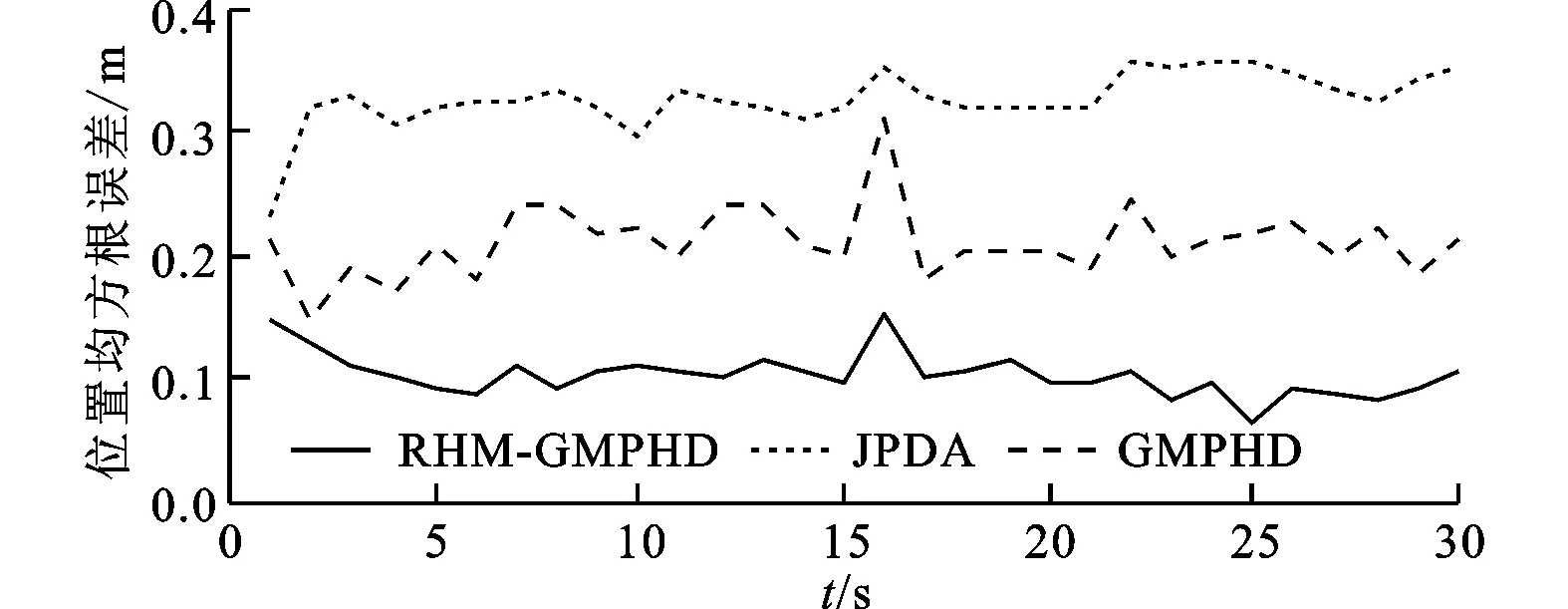
图4 位置均方根误差

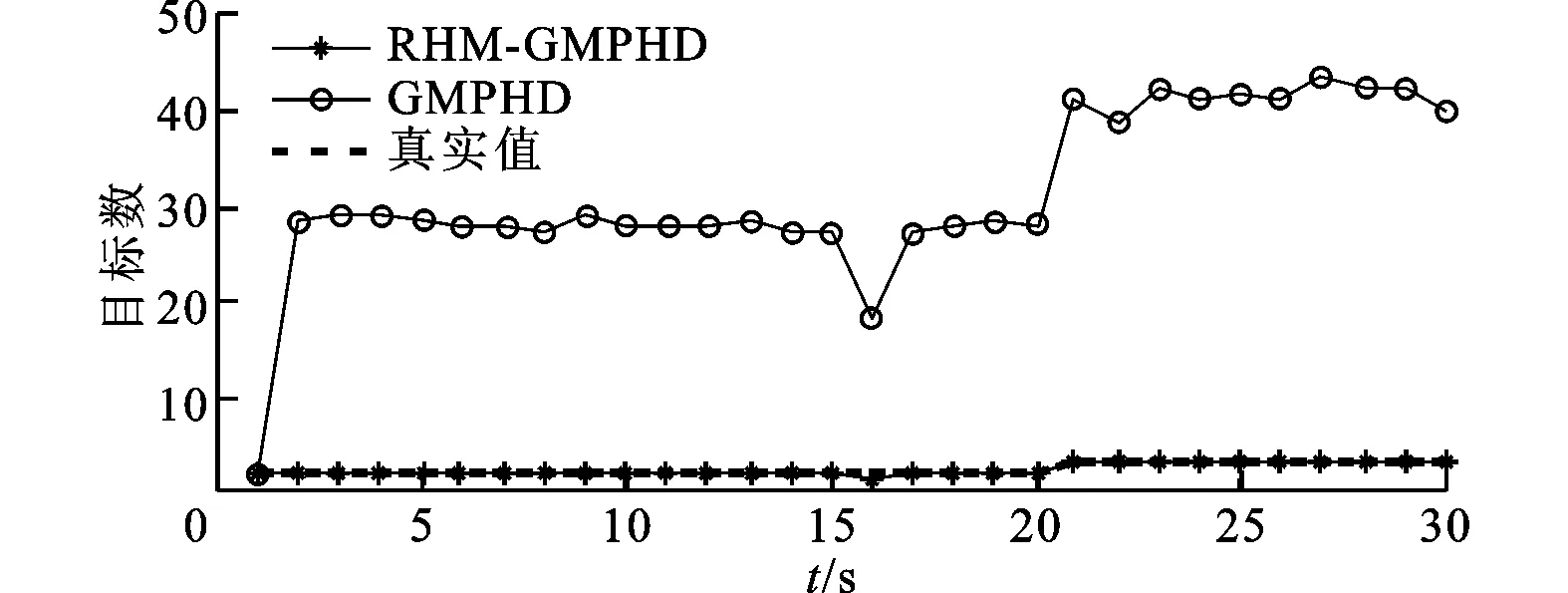
图5 真实与估计目标数

RHM-GMPHD滤波器对形状估计的Jaccard距离如图6所示,可知RHM-GMPHD滤波器对扩展目标形状也能较好地跟踪估计。在目标相交时,由于无法区分两目标量测信息而造成对形状估计的偏差增大,因此Jaccard距离会有所增加。当出现新生目标时,初始形状估计的误差也有所增加。

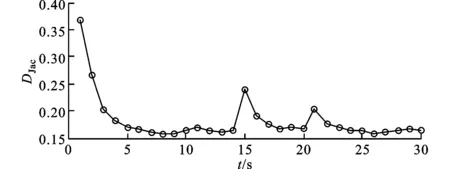
图6 真实形状与估计形状间的Jaccard 距离

4.3 凸星形群目标的跟踪

为了能够较好地评估RHM-GMPHD滤波器在跟踪形状发生动态变化的群时的性能,故不考虑新生目标。对2个群目标进行跟踪,群目标航迹与图3扩展目标1、2的航迹相同。群目标是由38个点目标组成的队列(群目标1的初始位置如图7所示),产生的量测服从均值为20的泊松分布。群目标的形状随时间发生变化,1～10s群目标形状不发生变化;10～20s各目标由质心向外扩散,目标尺寸增大;20～30s各目标向质心靠拢,形状尺寸减小。为得到JPDA、GMPHD和RHM-GMPHD滤波器在质心位置、数目及形状方面的估计性能,本文进行了100次Monte Carlo仿真实验,结果如图8～10所示。

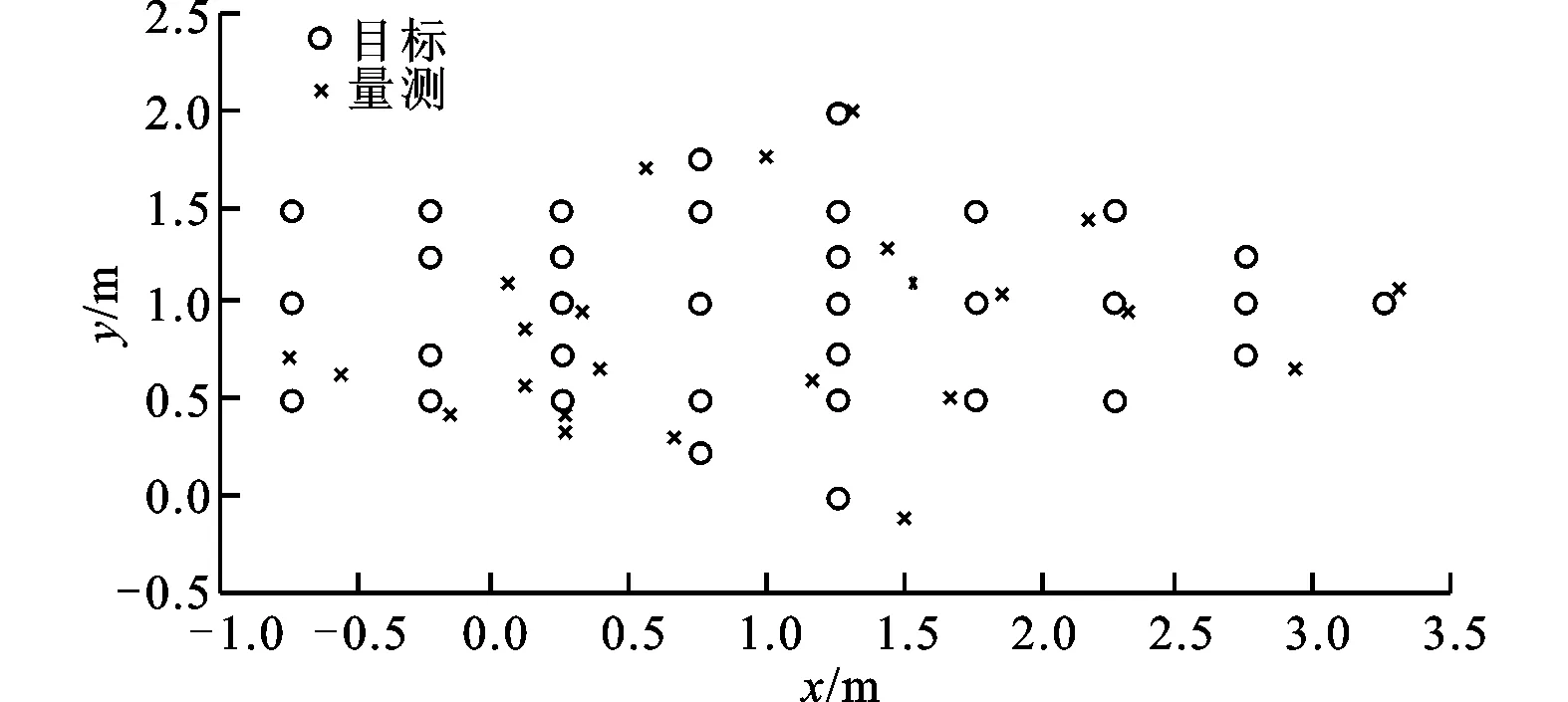
图7 群目标1的初始位置及量测

图8 位置均方根误差

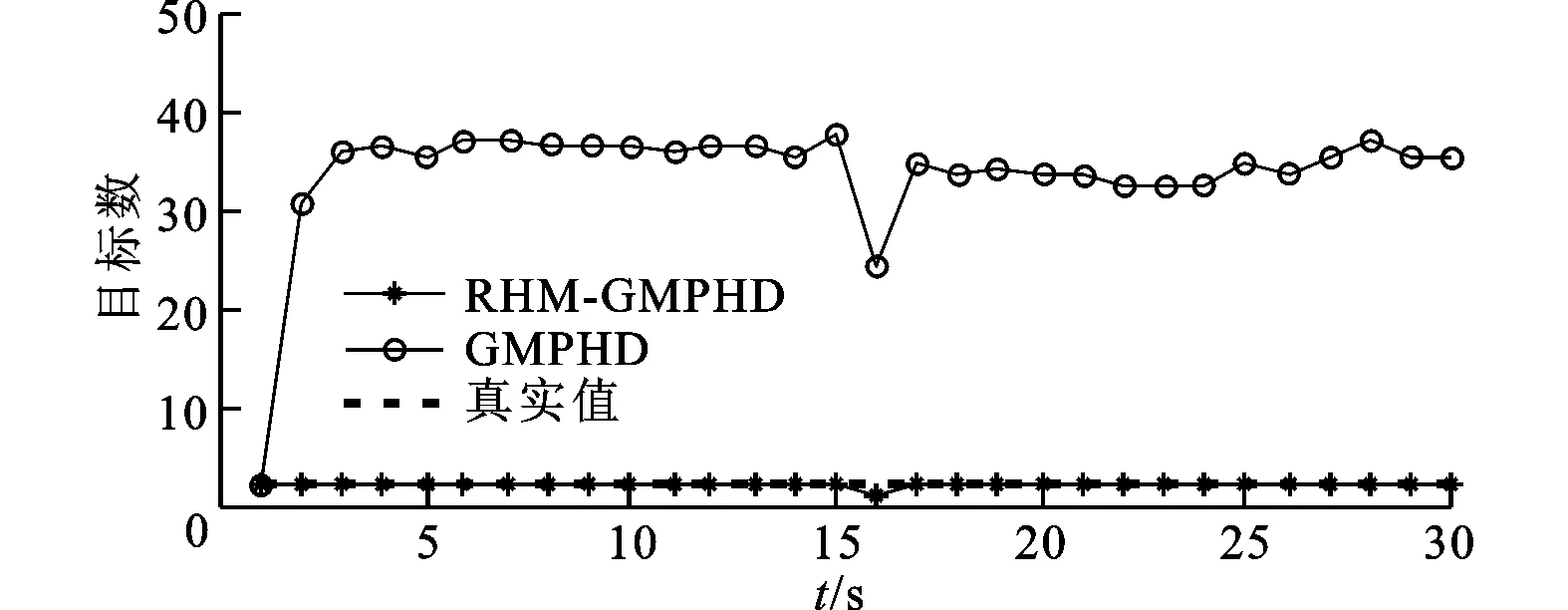
图9 真实与估计目标数

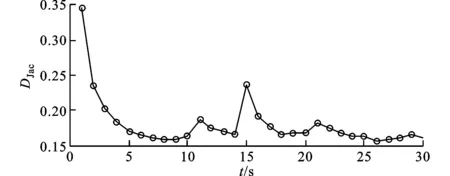
图10 真实形状与估计形状间的Jaccard距离

由图8～10可知,当群目标形状尺寸发生变化时,RHM-GMPHD滤波器也能较好地跟踪其质心位置和形状。在2个群目标合为一个群时,会造成质心位置估计的误差增大,但形状尺寸变化对估计性能影响不大,而形状尺寸的变化对JPDA和GMPHD滤波器的质心估计性能产生了较大的影响。由图9可得,RHM-GMPHD滤波器的目标估计数接近真实值,远远优于GMPHD滤波器。

图10中,将连接群目标边界上的点形成的曲线,视为群目标的实际形状。

5 结 论

本文提出的多扩展目标滤波器RHM-GMPHD,可以在杂波和漏检测下对任何凸星形扩展目标和群目标的运动状态和形状进行估计跟踪。推导了RHM-GMPHD滤波器的递推方程,讨论了多扩展目标滤波器对形状的性能评估,定义了几何形状间的Jaccard距离。仿真结果表明,即使目标转弯或事先指定的尺度因子的概率分布与实际不符,RHM-GMPHD滤波器也可以较好地跟踪多个凸星形扩展目标的位置和形状,并且能较好地跟踪形状动态变化的群目标的质心位置和形状。

[1] KOCH J W.Bayesian approach to extended object and cluster tracking using random matrices [J].IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042-1059.

[2] 连峰, 韩崇昭, 刘伟峰, 等.基于 SMC-PHDF 的部分可分辨的群目标跟踪算法 [J].自动化学报, 2010, 36(5): 731-741.

LIAN Feng, HAN Chongzhao, LIU Weifeng, et al.Tracking partly resolvable group targets using SMC-PHDF [J].Acta Automatica Sinica, 2010, 36(5): 731-741.

[3] FELDMANN M, FRANKEN D, KOCH J W.Tracking of extended objects and group targets using random matrices [J].IEEE Transactions on Signal Processing, 2011, 59(4): 1409-1420.

[4] BAUM M, HANEBECK U D.Random hypersurface models for extended object tracking [C]∥ Proceedings of International Symposium on Signal Processing and Information Technology.Piscataway, NJ, USA: IEEE, 2009: 178-183.

[5] BAUM M, HANEBECK U D.Shape tracking of extended objects and group targets with star-convex RHMs [C]∥ Proceedings of the International Conference on Information Fusion.Piscataway, NJ, USA: IEEE, 2011: 338-345.

[6] BAUM M, NOACK B, HANEBECK U D.Mixture random hypersurface models for tracking multiple extended objects [C]∥Proceedings of the IEEE Conference on Decision and Control.Piscataway, NJ, USA: IEEE, 2011: 3166-3171.

[7] WIENEKE W, KOCH J W.Probabilistic tracking of multiple extended targets using random matrices [C]∥Proceedings of Signal and Data Processing of Small Targets.Orlando, Florida, USA: SPIE, 2010: 419-430.

[8] MAHLER R.PHD filters for nonstandard targets: I Extended targets [C]∥Proceedings of the International Conference on Information Fusion.Piscataway, NJ, USA: IEEE, 2009: 915-921.

[9] ORGUNER U, LUNDQUIST C, GRANSTROM K.Extended target tracking with a cardinalized probability hypothesis density filter [C]∥Proceedings of the 14th International Conference on Information Fusion.Piscataway, NJ, USA: IEEE, 2011: 1-8.

[10]GRANSTROM K, LUNDQUIST C, ORGUNER U.Extended target tracking using a Gaussian mixture PHD filter [J].IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3268-3286.

[11]GRANSTROM K, ORGUNER U.A PHD filter for tracking multiple extended targets using random matrices [J].IEEE Transactions on Signal Processing, 2012, 60(11): 5657-5671.

[12]ZHANG D S, LU G J.Study and evaluation of different Fourier methods for image retrieval [J].Image and Vision Computing, 2005, 23(1): 33-49.

[13]VO B N, MA W K.The Gaussian mixture probability hypothesis density filter [J].IEEE Transactions on Signal Processing, 2006, 54(11): 4091-4104.

[14]潘磊, 雷钰丽, 王崇骏, 等.基于权重的Jaccard相似度度量的实体识别方法 [J].北京交通大学学报, 2009, 33(6): 141-145.

PAN Lei, LEI Yuli, WANG Chongjun, et al.Method on entity identification using similarity measure based on weight of Jaccard [J].Journal of Beijing Jiaotong University, 2009, 33(6): 141-145.

(编辑 刘杨)

Gaussian-MixtureProbabilityHypothesisDensityFilterforMultipleExtendedTargets

HAN Yulan1,ZHU Hongyan1,HAN Chongzhao1,WANG Jing2

(1.School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2.School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

A multiple extended-target Gaussian-mixture probability hypothesis density (RHM-GMPHD) filter, which provides the kinematic state and the extension state of extended targets, is proposed to address the difficultly estimated extension state.The pseudo-measurement likelihood function describing the relationship between kinematic state and extension state of extended target and measurements is constructed via the random hypersurface model(RHM) for convex-star extended target and sensor measurement function.Then the predicted state is considered, the update of extend target filter is derived to recursively estimate the kinematic state and extension state for extended targets.Moreover, the Jaccard distance is presented to evaluate the performance of the estimate extension state.Compared with the joint probabilistic data association(JPDA) and GMPHD filter, RHM-GMPHD provides the extension state and enhances the precision of the estimate number and the estimate kinematic state.Simulations indicate that the root-mean-square error of centroid from RHM-GMPHD gets 1/3of that from JPDA or 1/2 of that from GMPHD.The estimation number of extended targets approaches the true value, and Jaccard distance gets usually less than 0.2.

extended target tracking; Gaussian-mixture probability hypothesis density; random hypersurface model; estimate of the extension state

2013-09-27。

韩玉兰(1982—),女,博士生;朱洪艳(通信作者),女,副教授。

国家自然科学基金资助项目(61203220,61221063,61074176);国家“973计划”资助项目(2013CB329405)。

时间:2014-01-15

10.7652/xjtuxb201404017

TN274

:A

:0253-987X(2014)04-0095-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140115.1446.004.html