列车通信网络设计问题中的双层规划模型

田寅,贾利民,董宏辉,李海舰

(北京交通大学轨道交通控制与安全国家重点实验室, 100044, 北京)

列车通信网络设计问题中的双层规划模型

田寅,贾利民,董宏辉,李海舰

(北京交通大学轨道交通控制与安全国家重点实验室, 100044, 北京)

列车通信网络的物理拓扑结构和逻辑拓扑结构优化问题关系到列车控制系统及安全监测系统的性能和经济效益。对列车通信网络的设计问题进行建模,通过双层规划的思想,将列车通信网络的可靠性、建造费用与通信效率纳入统一的决策过程,从而建立科学的列车通信网络最优性能模型。上层规划以最低建造成本为目标,约束条件为网络可靠性;下层规划以最大通信效率为目标,约束条件为建造费用和网络物理拓扑。最后利用一种基于遗传算法和Floyd算法的混合求解过程对列车通信网络综合规划模型进行求解,得到满足网络稳定性要求下的最小费用设计方案及该方案下的最优效率通信方式。通过对实例结果的分析表明,文中提出的模型是切实有效的。

列车通信网络;双层规划;遗传算法;可靠性

随着网络通信技术的发展,越来越多的新型通信网络结构被提出,用于替代列车上原有的列车控制网络(TCN)。列车通信网络的拓扑结构将直接影响网络的性能,如果其结构设计不当,将会导致网络的可靠性下降,时延增加,从而进一步影响整体网络的性能。

目前,有大量优化网络拓扑结构设计的方法,其中大多数仅覆盖网络设计问题中的一部分,例如网络中的某些组成设备[1],或者某些特性[2],而没有系统化地对网络整体需求进行探讨。一些方法探讨了可靠性约束下的网络拓扑设计[3],以求建立一条稳定性最大的网络。一些方法探讨了如何根据费用约束及应用环境需求确定网络的物理拓扑结构,以获得最大可靠性[4],但是这些方法未考虑网络在时延方面的需求。一些文献探讨了网络中减小时延的方法[5-6],这些方法大多是在物理拓扑已知的网络中,通过对通讯协议或者某些设备的替换,来实现网络实时性的优化。此外,还有一些文献尝试探讨了如何对网络的物理拓扑和逻辑拓扑同时进行优化[7],但是没有提出一种较为通用的系统优化模型。一般而言,现有文献将这种同时考虑物理拓扑和逻辑拓扑的网络设计过程看作是一种多目标优化方法[8],但是这种思想导致算法求解变得异常复杂,并且不能确保获得最优解。

本文借助双层规划的思想[9]来实现在费用约束下,同时满足通信网络可靠性和实时性最优的设计过程。将列车通信网络的物理拓扑规划看作一个离散网络规划问题,将逻辑拓扑规划看作一个最短时延规划问题,本文基于这两个问题建立双层规划模型,并提出一种求解方法。

1 离散列车通信网络双层规划模型

1.1 用于求解离散网络规划问题的双层规划模型

列车控制系统的核心是列车通信网络,最重要的两个指标是可靠性和时延。由于受物理结构的限制,传统列车通信网络的可靠性和实时性存在一些缺陷。首先,传统列车通信网络内所有的节点串联在一起,整个网络呈线性链接,因此只要其中一条链路损坏,整个网络都将无法工作。另外,网络内部所传输的数据位于线状链路两端时会变得异常拥挤,从而使时延增大。

由于以太网技术已经被引入到列车通信网络设计中,本文尝试打破传统的节点间连接方式,通过有效地规划节点间的链路,实现网络可靠性和时延的最优化。受时延限制的列车通信网络拓扑规划问题可以表示为如下的双层规划模型

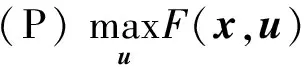
(1)

s.t.G(x,u)≤0

(2)

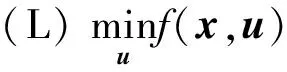
(3)

s.t.g(x,u)≤0

(4)

上述双层规划模型包含两个子模型,(P)为上层问题,也就是网络物理拓扑规划问题;(L)是下层问题,也就是网络逻辑拓扑规划问题;F和u是物理拓扑规划问题的目标函数和决策向量;G是(P)问题的决策向量的约束条件;f和x是逻辑拓扑规划问题的目标函数和决策向量;g是(L)问题的决策向量的约束条件。

1.2 物理拓扑优化问题

传统意义上,在研究通信网络的可靠性问题时,假定节点和链路的可靠性是随机而且相互独立的,但是这些可靠性都已知并且固定。由于列车通信网络上所有信息都是双向传输,因此可用无向图来描述列车通信网络。假设G=(N,L,A)是一个没有平行链路的网络,并且网络中没有孤立点存在,则费用约束的网络可靠性优化问题(即上层物理拓扑优化)可以用如下模型来表示

(5)

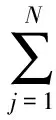
(6)

P(lj)=F1(c(lj))

(7)

P(ni)=F2(c(ni))

(8)

式中:R(x)是整个网络的可靠性;P(lj)是链路lj的可靠性;P(ni)是节点ni的可靠性;Ω是网络所有可用状态的集合;C(x)是整个系统的最大可使用费用;c(lj)是每单位距离链路j的费用;dj是链路j的长度;c(ni)是节点i的费用;L是链路个数;N是节点个数;F1是链路可靠性与链路单价之间的函数关系;F2是节点可靠性与节点成本之间的函数关系。在任意时间段,G中都只有部分链路能够工作,此时G的状态是有向图(N,L,A)的子图(N,L′),其中L′是正常工作链路的集合。如果lj∈L′,那么uj=1,否则uj=0。

在上层的物理拓扑优化问题中,网络设计者的目标是通过改变连接方式来获得最大的网络可靠性。约束条件(6)保证了网络的建设总费用不会超过规定的最大费用,约束条件(7)和(8)描述了网络设备的可靠性与费用之间的函数关系。

1.3 逻辑拓扑优化

逻辑拓扑优化的目标是使传输时延最短。同传统列车通信网络中传输的控制指令大小相比,以太网能承载的数据量非常巨大,因此假设网络带宽足够大,不会影响数据的实时性。这样,数据流的逻辑拓扑优化问题实际上是一个在网络物理拓扑限定下的最小时延问题。列车通信网络的逻辑拓扑优化问题(即下层逻辑拓扑优化)可以表述为

(9)

s.t.Φ∈Ω

(10)

c(lj)=f1(t(lj))

(11)

c(nj)=f2(t(nj))

(12)

式中:T(x)是系统的总时延;t(lj)是链路lj上的延时;t(ni)是节点ni的延时;数据从节点向另一任意节点传输时,通过的传输路径是G的一个子集,记做(N′,L″);f1是链路时延与链路单价之间的函数关系;f2是节点时延与节点成本之间的函数关系。

在这个模型中,网络的设计者希望信息按照设定的方式传输,因此网络的下层规划实际上是在物理拓扑一定的情况下,对逻辑拓扑进行优化的过程。约束条件(10)保证了逻辑链路的选择是在已知的物理拓扑下完成的,约束条件(11)和(12)描述了网络设备的时延与费用之间的函数关系。

2 列车通信网络双层规划模型求解

一般情况下,双层规划的优化问题是很难求解的[10]。对通信网络可靠性、时延及成本的优化问题是一个NP-C问题,因此遗传算法是一种合适的求解方法,近年来已经被大量地用于非线性问题的优化中。大量的文献研究表明,遗传算法可以有效地解决网络性能优化的问题[11]。

在通常情况下,某种设备的可靠性与费用成正比,时延与费用成反比。因此,模型下层L1中的费用约束条件可以通过特定的费用转移至上层约束中,以便于模型的求解。

根据列车通信网络双层规划模型的特点,本文采用模块化的设计思想,提出一种基于遗传算法与Floyd算法的求解过程,算法步骤如下。

步骤1设定初始参数,包括节点数目、节点间距离、最大费用、节点单价、节点可靠性、链路单价和链路可靠性。

步骤2根据初始参数,生成初始基因并利用遗传算法对节点间的物理连接方式进行规划,并在最大费用约束条件下,生成最优解。

步骤3判断物理拓扑结构是否符合实际要求,如果符合,进入步骤4。否则,将该结果记录进不合适解数据库后进入步骤2,重新寻找除去不合适解外的最优解。

步骤4将最优解的基因转化成表征物理拓扑结构的邻接矩阵,并传递给逻辑拓扑规划模块。进行逻辑拓扑规划,寻找网络中任意两个节点间的时延最小的通信方式,生成节点间逻辑拓扑规划表。

步骤5判断逻辑拓扑是否符合要求,如果符合要求,结束全部算法。否则,将该结果记录进不合适解数据库并判断原因,如果是逻辑拓扑规划导致,则重新进行步骤4,否则进行步骤2。

2.1 求解逻辑拓扑优化问题的遗传算法

2.1.1 编码方式 在双层规划过程中,非常关键的一个步骤是如何有效地将信息在两层优化中传递,其中有效的基因编码方式又是十分重要的一部分。基因编码的第一步是确定基因的长度。对于一个有Nd个节点的列车通信网络,其包含的链路数Nl与节点数Nd之间的关系为

(13)

因此,为了表征整体网络的可靠性,本文提到的算法中所用的基因应该有0.5(Nd+1)Nd+Nd位,开始的|0.5(Nd+1)Nd|位表征链路的可靠性,接下来的|Nd|位表征节点的可靠性。

对于不同的节点及链路,用不同的整数代表其可靠性,例如数字1代表可靠性最好的设备,数字2代表可靠性次之的设备等等。如果有N种不同可靠性的设备,那基因中每一个位的取值范围是[0,N],其中0代表链路不存在。

与传统的用遗传算法求解网络可靠性的研究不同,本文所提方法除了得出最优解外,还需要将网络结构传递至下层的逻辑拓扑规划,因此基因的编码必须要能体现出被传递网络的结构特征。通常利用网络的伴随矩阵来表征网络结构,因此基因的结构也从伴随矩阵中演变而来。图1显示了网络的伴随矩阵a与基因g的关系。

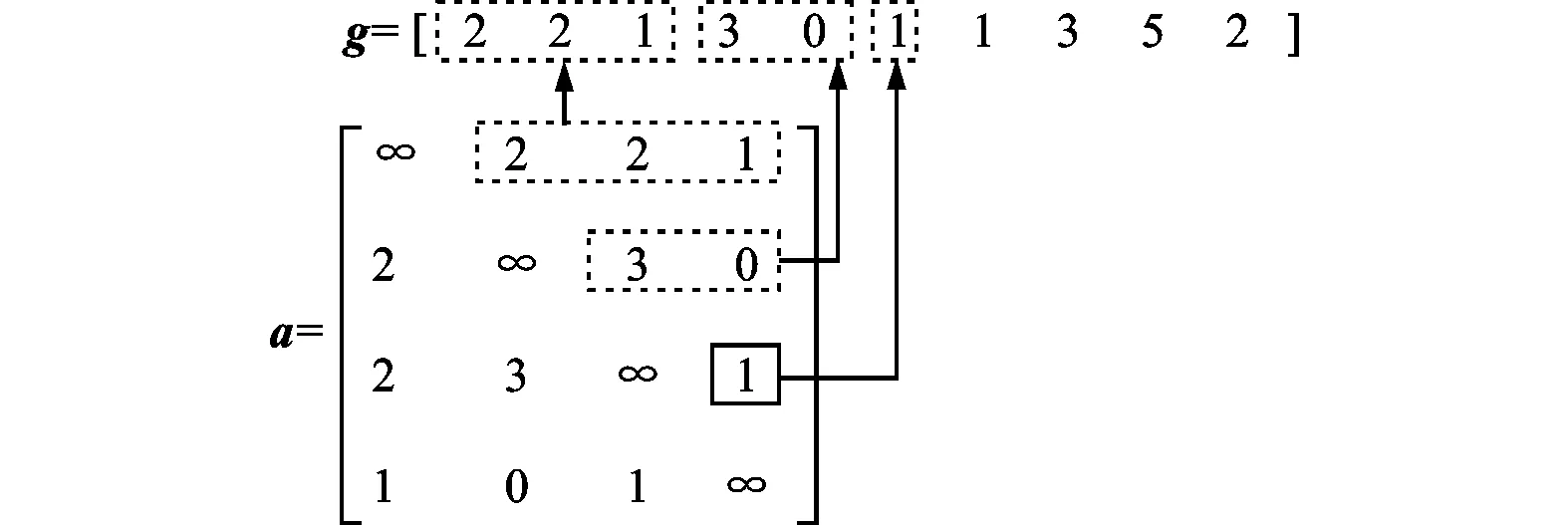
图1 基因与伴随矩阵的关系

2.1.2 适应度函数 优化的目标是寻找费用约束条件下最可靠的物理拓扑结构,因此适应度函数必须包含费用和可靠性两个因素。由于处于最优边界上的解往往是一个可行解和一个不可行解的后代,因此在设置适应度函数时,不能单纯地将不可行解剔除。合理的解决方案是设置一种有效的惩罚函数,用以降低不可行解在种群中的比重。根据实际实验发现,采用如下适应度函数具有较好的运算效率

(14)

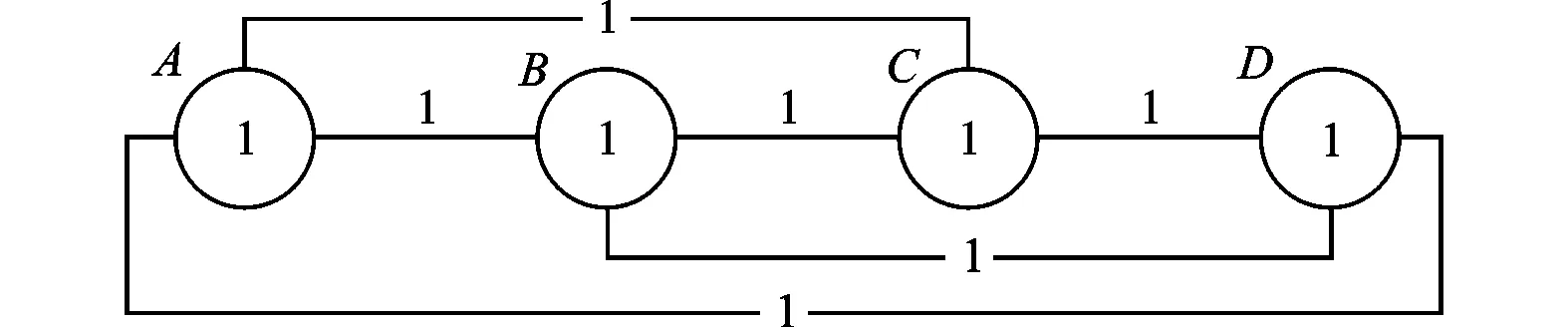
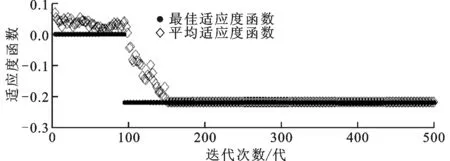
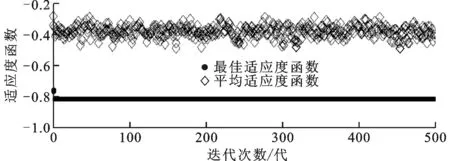
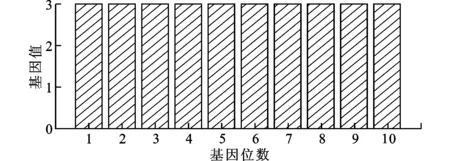
式中:C是系统允许的最大费用;count(r(g))≠0表示g的可达矩阵r(g)中0的个数,该限制条件保证了列车通信网络中不会存在孤立节点;R(x)是系统可靠性;c(x)是系统实际费用;λ是惩罚因子,根据实际情况设定,λ

2.1.3 基因操作 种群数量、选择方法、交叉及变异操作、停止条件等参数决定了遗传算法的效率。通过大量的实验,选择出最适合本文中算法的遗传算法参数。种群数量为400,同时限制种群中每个基因的取值范围为1到N的整数。采用随机均匀的基因筛选方法,使用交叉概率为0.8的单点交叉方法,使用突变率为0.03的均匀突变,终止条件为遗传500代。

2.2 求解逻辑拓扑优化问题的算法

首先假设列车通信网络中各节点间的最小通信时延仅与节点间的最短路径有关,并且最短路径与链路长度无关,也就是网络中一条信息传递的时间只与其经过的节点数有关。下面说明该假设的合理性。

众所周知,通信网络的时延为

T=Ttd+Tpd+Tqd

(15)

式中:Ttd是发送时延;Tpd是传输时延;Tqd是排队时延。但是,对于列车通信网络来说,最大链路长度不会超过200m,因此网络中的传输时延可忽略不计。发送时延与排队时延都是由转发产生的,所以在对网络通信时延进行最优化时,只考虑信息传递过程中经过了多少次转发,也即经过了多少个节点。

由于优化目标是寻找列车通信网络系统内每一个节点与其他节点通信时的最短路径,这属于一种全局最短路问题,因此可采用Floyd算法。该算法已经大量地应用于网络最短路问题的求解过程中。对本文所提方法而言,运用Floyd算法关键是将上层物理规划中获得的最优基因转换成求解Floyd算法所需要的伴随矩阵。本文方法是利用3.1节中基因g与伴随矩阵a的关系,重新将基因转化成伴随矩阵。

3 数值算例

通过两个算例验证了本文所提算法的准确性和有效性,并给出实际问题的解决案例。

3.1 算例1

假设有3种不同可靠性及费用的链路及节点,如表1、表2所示。

表1 链路可靠性与费用关系对照表

表2 节点可靠性与费用关系对照表

另假设网络中有4个节点成线性排列,相邻节点间隔40m。经计算可知,要实现这样一个系统,其最小费用是6960,结构如图2a所示,此时的网络可靠性最小,为0.22。最大费用是18 000,结构如图2b所示,此时的网络可靠性最大,为0.81。

(a)4个节点时费用最低的解

(b)4个节点时费用最高的解

下面用本文设计的算法,分别将费用约束设定为6960及18 000,惩罚因子λ=0.1,观察运行得到的结果是否符合实际情况。算法运行完成后的结果如图3、图4所示。由图3可见,费用约束为6960时,在100代左右出现最优解,最优解约为0.2202。由图4可见,费用约束为18 000时,约在第10代出现最优解,最优解约为0.814 7。可知,利用本文提出的列车通信网络双层规划算法,上层物理拓扑规划及下层逻辑拓扑规划都能够产生符合要求的解。

(a)费用为6960时的迭代结果

(b)费用为6960时的基因

(a)费用为18 000时的迭代结果

(b)费用为18 000时的基因

3.2 算例2

假设现在有一个6节车厢编组的列车,每节车厢中有一个节点需要与其他车厢中的节点连接。该6节编组列车原型为广州地铁2号线上运行的车辆,每节车长26m。考虑布线方式,假设要连接相邻两个节点,需要50m的电缆。链路及节点的费用和可靠性仍然参考表1和表2。分别求解最大建造费用为17 000及25 000时,最稳定网络结构及最短时延通信方式。考虑信号衰减问题,系统中的最大链路长度必须小于或等于150m。

利用本文所述方法,得到列车中节点连接方式的最优解物理连接方式如图5所示,图中从左至右依次为A-F节点。C(x)=17 000时,最佳逻辑链路为A-B;A-C;A-C-D;A-C-E;A-C-E-F;B-C;B-D;B-D-E;B-D-F;C-D;C-E;C-E-F;D-E;D-F;E-F。C(x)=25 000时,最佳逻辑链路为A-B;A-C;A-D;A-D-E;A-D-F;B-C;B-D;B-D-E;B-D-F;C-D;C-D-E;C-F;D-E;D-F;E-F。

(a)C(x)=17 000

(b)C(x)=25 000

对比两个不同限制的优化条件可以发现:随着费用的增加,列车通信网络系统的可靠性增加;由于链路数目的增加,网络系统的时延也在降低。可以发现,在费用有限时,应该尽可能地增加链路数目,形成冗余连接,而不是选用高可靠性的设备。

4 结 论

本文提出了列车通信网络优化问题的普适描述,以及一种能够在费用约束下得到列车通信网络可靠性及时延同时最优的设计方法。通过双层规划的思想,本文将列车通信网络设计问题分成位于上层的物理拓扑规划问题及位于下层的逻辑拓扑规划问题,完整地实现了列车通信网络的优化过程。

本文提出列车通信网络双层规划模型的求解方法。通过改进的遗传算法,本文设计了合理的基因表示方法,结合遗传算法与Floyd算法,有效地将物理拓扑优化结果传递至下层优化过程中。

本文所提方法能够有效地寻找到费用、可靠性及时延三者的平衡点,并且由于采用了模块化的设计,该方法便于更换约束条件,以适用于不同目的和特定约束的列车通信网络优化问题。

通过实例分析可知,本文所提方法是合理的,并且能够解决相应的实际问题,但该方法没有考虑链路在通过车厢时的可靠性变化问题,这个问题可作为逻辑拓扑设计问题中的一个附加条件。虽然这一问题并不会改变本文算法中费用、可靠性及实时性的关系,但是会影响实际施工过程中对设备的选择,这将是未来的一个研究方向。

[1] MORENO J C, LALOYA E, NAVARRO J.A link-layer slave device design of the MVB-TCN bus [J].IEEE Transactions on Vehicular Technology, 2007, 56(6): 3457-3468.

[2] 邢震, 贾步超, 穆建成, 等.基于交换式以太网的TCN设计与实时性能分析 [J].铁路计算机应用, 2013, 22(6): 51-56.

XING Zhen, JIA Buchao, MU Jiancheng, et al.Design and real-time performance analysis on switched ethernet based train communication network [J].Railway Computer Application, 2013, 22(6): 51-56.

[3] SZLACHCIC E.Fault tolerant topological design for computer networks [C]∥Proceedings of the 2006IEEE International Conference on Dependability of Computer Systems.Piscataway, NJ, USA: IEEE, 2006: 150-159.

[4] SHAO Fangming, SHEN Xuemin, HO Pinhan.Reliability optimization of distributed access networks with constrained total cost [J].IEEE Transactions on Reliability, 2005, 54(3): 421-430.

[5] UNZUETA H, JIMENEZ J, MARTIN J L, et al.An emulator to develop the Wire Train Bus protocol stack [C]∥Proceedings of the 32nd Annual Conference on IEEE Industrial Electronics Society.Piscataway, NJ, USA: IEEE, 2006: 3721-3726.

[6] 赵洪华, 陈鸣.利用往返时延抖动的网络拓扑推断算法 [J].西安交通大学学报, 2009, 10(2): 28-32.

ZHAO Honghua, CHEN Ming.A topology inference algorithm using round delay variation [J].Journal of Xi’an Jiaotong University, 2009, 10(2): 28-32.

[7] FENCL T, BURGET P, BILEK J.Network topology design [J].Control Engineering Practice, 2011, 19(11): 1287-1296.

[8] WANG Chenshu, CHANG Chingter.Integrated genetic algorithm and goal programming for network topology design problem with multiple objectives and multiple criteria [J].IEEE/ACM Transactions on Networking, 2008, 16(3): 680-690.

[9] CHEN Yongrong.Model and algorithm for discrete network equilibrium design problem [C]∥Proceedings of the 2nd International Conference on Uncertainty Reasoning and Knowledge Engineering.Piscataway, NJ, USA: IEEE, 2012: 166-169.

[10]VICENT L N, CALAMAI P H.Bilevel and multilevel programming: a bibliography review [J].Journal of Global Optimization, 1994, 5(3): 291-306.

[11]KUMAR A, PATHAK R M, GUPTA Y P.Genetic-algorithm-based reliability optimization for computer network expansion [J].IEEE Transactions on Reliability, 1995, 44(1): 63-72.

[本刊相关文献链接]

郑豪,张兴军,王恩东,等.一种采用驱动隔离的宿主机可靠性方法.2013,47(10):7-12.[doi:10.7652/xjtuxb201310002]

王兆杰,高峰,翟桥柱,等.高耗能企业关口平衡问题的双目标规划模型.2013,47(8):26-32.[doi:10.7652/xjtuxb201308005]

汪志伟,曹建福,郑辑光.一种面向分簇无线传感器网络的多信道跨层协议.2013,47(6):61-67.[doi:10.7652/xjtuxb 201306011]

李硕,王学望,康锐.面向完整性要求的航空电子全双工交换式以太网可靠性评价参数研究.2013,47(3):126-131.[doi:10.7652/xjtuxb201303023]

伍文,孟相如,马志强,等.模块化动态博弈的网络可生存性态势跟踪方法.2012,46(12):18-23.[doi:10.7652/xjtuxb 201212004]

宋婧,丛犁,葛建华,等.双层网络中一种协作博弈的动态资源分配方法.2012,46(10):89-94.[doi:10.7652/xjtuxb2012 10016]

覃庆努,魏学业,韩磊,等.电子系统的Markov模型和云可靠性评价方法.2012,46(8):87-93.[doi:10.7652/xjtuxb 201208016]

杨柳静,秦涛,王晨旭.应用交互式网络流模型的高速网络异常行为检测与控制.2012,46(6):58-65.[doi:10.7652/xjtuxb201206011]

侯重远,江汉红,芮万智,等.工业网络流量异常检测的概率主成分分析法.2012,46(2):70-75.[doi:10.7652/xjtuxb 201202012]

刘逵,刘三阳,冯海林.双信道无线传感器网络移动代理路由算法.2012,46(2):113-118.[doi:10.7652/xjtuxb201202019]

张文健,田茂,何浩,等.分层网络下行中断概率的闭式表达.2011,45(12):59-63.[doi:10.7652/xjtuxb201112011]

鄢民强,杨波,王展.不完全覆盖的模糊多状态系统可靠性计算方法.2011,45(10):109-114.[doi:10.7652/xjtuxb201110020]

张莹,殷勤业,穆鹏程.利用均匀线阵实现高移动性通信系统中的多普勒补偿.2011,45(8):73-77.[doi:10.7652/xjtuxb 201108013]

池信泽,周颢,赵保华.面向前向纠错的无线Mesh网多播差错控制协议.2011,45(8):30-36.[doi:10.7652/xjtuxb2011 08006]

李黎,管晓宏,赵千川,等.网络生存适应性的多目标评估.2010,44(10):1-7.[doi:10.7652/xjtuxb201010001]

(编辑 武红江)

BilevelProgrammingModelofTrainCommunicationNetworkDesign

TIAN Yin,JIA Limin,DONG Honghui,LI Haijian

(State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong Unversity, Beijing 100044, China)

Train communication network physical topology and logical topology optimization usually drive the performances and economic benefits of the train control system and safety monitoring system.A model for designing train communication network is established.Following the essence of bi-level programming, the reliability, construction cost and communication efficiency are taken into account in decision-making process to suggest a scientific optimal performance model for designing train communication network.At the upper level, lowering construction cost is taken as the objective and constrained by network reliability.At the lower level, the maximum communication efficiency is taken as the objective and constrained by construction cost and physical topology.A hybrid method based on both genetic algorithm and Floyd algorithm is used to obtain an approach with higher reliability and lowest cost , and an example verifies the effectiveness of this model.

train communication network; bi-level programming; genetic algorithm; reliability

2013-09-20。

田寅(1986—),男,博士生;贾利民(通信作者),男,教授。

国家高技术研究发展计划资助项目(2011AA110505);北京市科技新星计划资助项目(Z1211106002512027)。

时间:2014-01-16

10.7652/xjtuxb201404023

U283.2

:A

:0253-987X(2014)04-0133-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140116.1601.002.html