红外地球敏感器修正的卫星姿态角动量反馈控制

苏威,洪涛,徐川,郝培杰

(1.宇航动力学国家重点实验室, 710043, 西安; 2.西安卫星测控中心, 710043, 西安)

红外地球敏感器修正的卫星姿态角动量反馈控制

苏威1,2,洪涛2,徐川2,郝培杰2

(1.宇航动力学国家重点实验室, 710043, 西安; 2.西安卫星测控中心, 710043, 西安)

针对角速度陀螺故障的低轨三轴稳定卫星因角速度测量数据缺失而导致卫星姿态失控的问题,提出了一种红外地球敏感器修正的角动量反馈控制方法。该方法利用动量轮转速与卫星角速度之间的数值变化关系,以红外地球敏感器实测弦宽为基准,建立角动量反馈控制的最小二乘修正模型,并通过蒙特卡洛方法迭代出角动量反馈控制的最优系数,从而由卫星控制器件中反演出连续的卫星角速度信息,最终实现陀螺故障情况下的卫星三轴稳定姿态控制。仿真结果表明:所提方法能够准确建立动量轮角动量与卫星角速度之间的对应关系,使得卫星姿态控制的稳定性较好;从系统重组的角度为卫星的故障处理提供了新途径,且有效延长了卫星的使用寿命。

角动量反馈;姿态控制;最小二乘方法

卫星的角速度信息对于低轨三轴稳定卫星的姿态控制极为重要,其数据大多直接来源于角速度陀螺[1]。随着卫星的长期在轨运行,高速旋转的陀螺会因故障而失效[2],使得卫星实施姿态调整的角速度依据缺失,这种情况下卫星的角速度信息需要通过新的途径重新获取。作为姿态控制执行器件的动量轮,其隐含着卫星的角速度信息[3],具有角速度陀螺测速功能。然而,在卫星的实际在轨运行中,卫星角速度与动量轮的准确数值关系很难直接得到,原因是:角动量测量存在误差[4],卫星长期在轨运行导致星体转动惯量变化[5],卫星挠性特性存在不确定性[6],这些问题使得角动量反馈控制实施困难。为此,本文从系统重组[7]的角度提出了一种新的角动量反馈控制方法,其利用红外地球敏感器的实测数据,对卫星角速度和动量轮的数值关系进行修正,进而在卫星角速度陀螺发生故障[8]的条件下实施姿态控制,使得卫星姿态处于相对稳定的状态。

1 红外地球敏感器实测数据修正下卫星姿态角动量反馈控制

1.1 角动量反馈控制修正模型

在小运动假设下,稳定运行模式的卫星姿态动力学方程为[9]

(1)

式中:Φ为姿态角;I为卫星绕滚动、俯仰和偏航3个本体坐标轴的转动惯量;T为控制力矩;ω为挠性模态频率;pi为刚体与挠性模态运动的耦合系数;qi为挠性模态坐标,i=1,2,…n,n为模态个数。

在稳态模式下,卫星姿态控制的主要执行器件为动量轮。动量轮相对于其转轴的转动惯量记为Iω,相对于星体的转速为ωM,则动量轮自旋角动量Hω=IωωM。根据动量矩定理导出

(2)

由式(1)、(2)得

(3)

式中:C为整星存储的角动量常数。

令角动量的变化量ΔH=Hω-C,由式(3)得

(4)

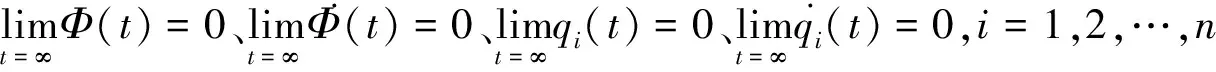
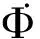
(5)

式中:kp、ki、kd分别为比例、积分、微分回路的控制系数,由姿态控制系统的收敛特性决定。

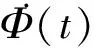
(6)

式中:k1、k2、k3分别为待定的角动量反馈修正系数。

将式(6)代入式(5)得

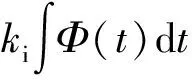
(7)

式(7)即为修正的角动量反馈控制力矩模型。可以看出,适当选择k1、k2、k3,在非连续角速度测量下可以维持原姿控系统的稳定性和收敛性。

1.2 基于最小二乘的角动量反馈修正系数

由式(6)积分得

(8)

Φ(t)设为滚动角或俯仰角,通过红外地球敏感器直接测量地心角,可以计算得到Φ(t)[10],ΔH(t)则为实测角动量在滚动和俯仰方向的变化量。

以某卫星为例,该卫星中搭载了2个共面安装的圆锥扫描式红外地球敏感器,2个红外地球敏感器的扫描圆锥对称轴与地垂线在同一平面内。在以星体质心为中心的天球面上,标称状态大圆弧的中点即为地中。

当2个红外地球敏感器处于标称状态时,地心角η1、η2等于标称地心角η*,而η*由红外地球敏感器的安装角决定。当滚动角为φ、俯仰角为0时,2个红外地球敏感器测得的地心角分别为

η1=η*-φ;η2=η*+φ

(9)

滚动角φ=0.5(η2-η1)

(10)

当俯仰角为θ、滚动角为0时,2个红外地球敏感器测得的地心角满足

η1=η2>η*

(11)

偏航角ψ=arccos(cosη1/cosη*)

(12)

当俯仰角和滚动角均不为0时,2个红外地球敏感器测得的地心角满足

η1+η2>2η*,η1≠η2

(13)

偏航角、滚动角分别为

ψ=arcsin(sinη2sinA)

(14)

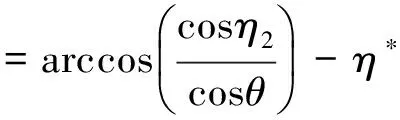
(15)

(16)

当姿态角为滚动角时,Φ为φ;当姿态角为俯仰角时,Φ为θ。由此得到Φ与实测地心角η1、η2之间的函数关系f(η1,η2),因此式(8)可表示为

(17)

实际遥测中,实测弦宽和角动量均为离散采样值,由于角动量的采样频率远大于弦宽的采样频率,因此式(17)可以改写为

f(η1(ti),η2(ti))-f(η1(tj),η2(tj))=

k3(ti+mΔt))ΔH(ti+mΔt)Δt

(18)

式中:ti、tj分别为连续的2次地心角采样时刻;Δt为角动量的采样间隔;m为0～M的整数,M=tj-ti/Δt。令

k3(ti+mΔt))ΔH(ti+mΔt)Δt

Ci为由角动量实测数据得到的ti、tj时刻滚动或俯仰角度差计算值。令

Oi=f(η1(ti),η2(ti))-f(η1(tj),η2(tj))

Oi为由实测红外地球敏感器弦宽换算得到的ti、tj时刻滚动和俯仰角度差值。

基于最小二乘算法的角动量反馈系数修正模型如下

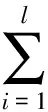
(19)

式中:ε为误差;l为实测数据的观测次数。

对于式(19),利用Monte Carlo方法[11],可以计算得到角动量反馈修正系数。通过式(19)建立优化函数

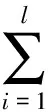
(20)

定义模函数

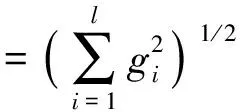
(21)

选取初值k1、k2、k3,代入式(21)计算G0=‖G‖;再选取正数b,在区间[-b,b]上随机产生均匀分布的一系列三维数组(k1,k2,k3)。对于每一个三维数组(k1,k2,k3),计算(k1+r,k2+r,k3+r)的模函数G1,直到|G1|<|G0|为止,此时令k1=k1+r,k2=k2+r,k3=k3+r。若连续产生了m个随机数(m的大小取决于计算机的运算能力)仍不能满足|G1|<|G0|,则将b减半后重复上述运算,直到|G0|<ε(ε为预先设定的阈值)为止,此时的k1、k2、k3即为所求的角动量反馈系数。将该k1、k2、k3代入式(7),即可得到卫星的控制力矩。

2 卫星实际在轨应用效果验证

以某卫星为例,卫星中共安装了6个饱和值为30N·m·s的动量轮h1～h6,安装结构如图1所示,图中X为滚动轴,Y为俯仰轴,Z为偏航轴。卫星整星转动惯量约为[3500,4 200,6000] kg·m2,且处于偏置动量控制模式。

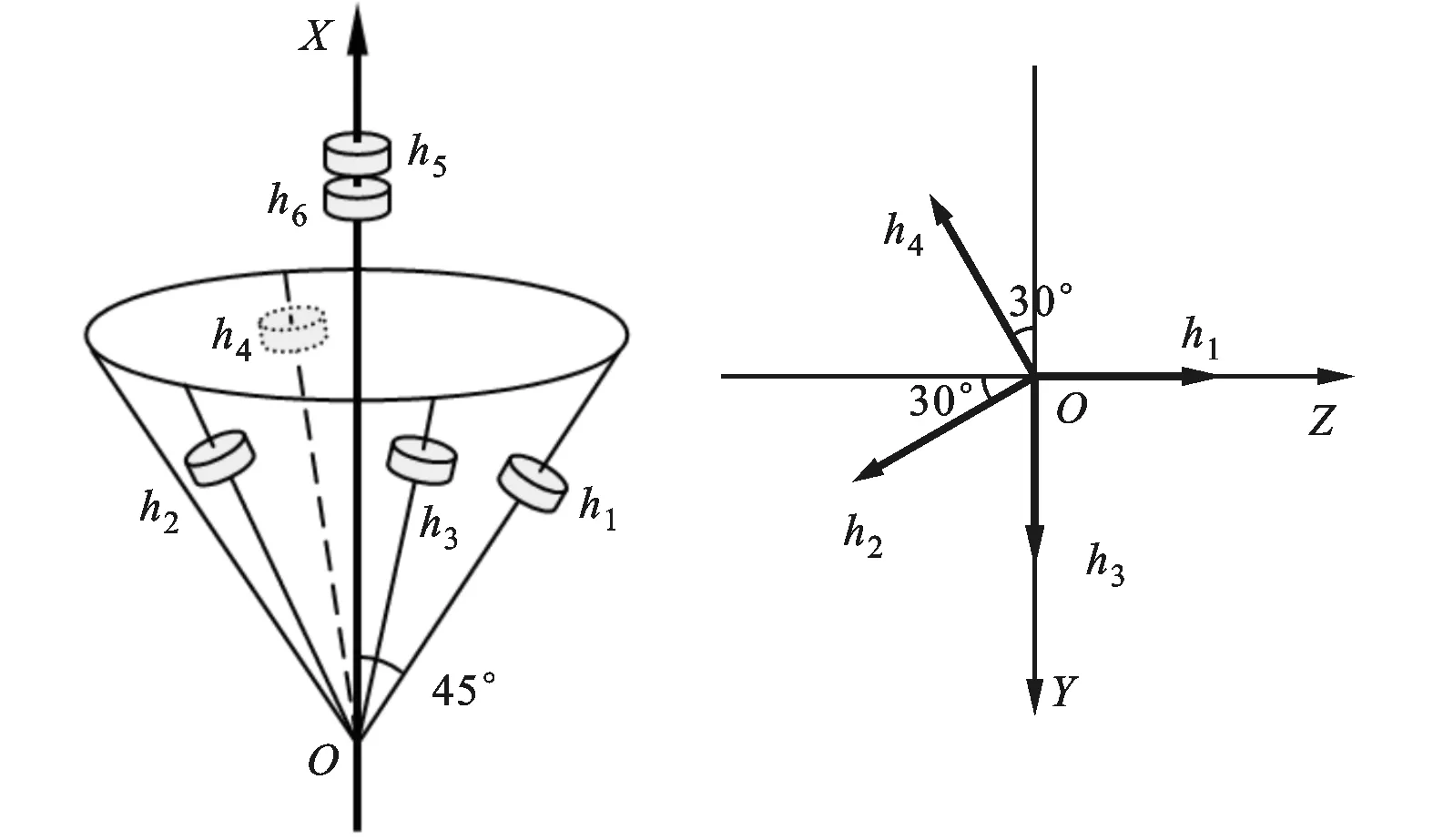
图1 某卫星动量轮安装结构

引入角动量反馈控制后,在50ks内的姿态控制结果如图2～4所示。

图2 角动量控制的动量轮角动量变化

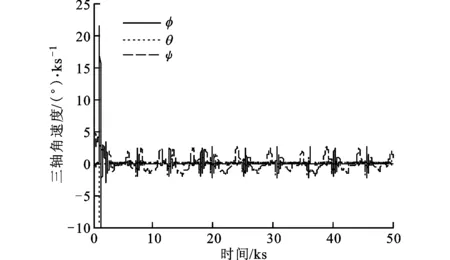
图3 角动量控制的三轴姿态角速度曲线

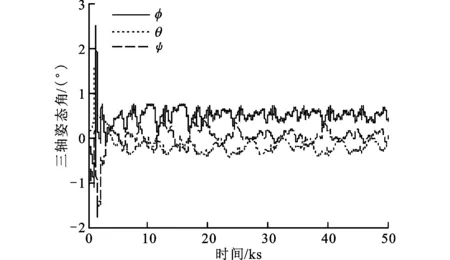
图4 角动量控制的三轴恣态角曲线

对比图2和图3可以看出,动量轮角动量随卫星三轴姿态角速度的变化而实时变化,且变化趋势基本相同,说明本文提出的控制方法通过最小二乘算法和Monte Carlo方法迭代出的角动量反馈系数,可以准确建立动量轮角动量与卫星三轴姿态角速度之间的对应关系。从图3还可以看出,三轴姿态角速度逐渐收敛,最终稳定在0.003(°)/s以内,卫星姿态得到了有效控制。图4表明,姿态控制误差在1.5°以内,系统的稳定性较好。

3 结 论

随着卫星长期在轨运行,高速旋转的角速度陀螺往往容易出现不可恢复的硬件故障,此类故障很难通过陀螺本身进行维修和恢复。本文提出的角动量反馈控制方法从系统重组的角度为该类故障处理提供了新途径,也具有应用和推广价值。尤其在卫星多组冗余陀螺仅剩最后一组可用时,将最后一组正常工作的陀螺通过断电进行保护,在变轨或异常处理期间开启使用,而在其他日常工作期间,通过本文提出的角动量反馈控制来稳定卫星姿态,可有效延长卫星的使用寿命。

[1] 钱山, 李鹏奎, 张士峰, 等.基于改进陀螺漂移模型的卫星姿态确定算法 [J].宇航学报, 2009, 30(2): 585-589.

QIAN Shan, LI Pengkui, ZHANG Shifeng, et al.Satellite attitude estimation based on improved model of the gyro random drift [J].Journal of Astronautics, 2009, 30(2): 585-589.

[2] 张森, 石军, 王九龙.卫星在轨失效统计分析 [J].航天器工程, 2010, 19(4): 41-46.

ZHANG Sen, SHI Jun, WANG Jiulong.Satellite on-board failure statistics and analysis [J].Spacecraft Engineering, 2010, 19(4): 41-46.

[3] 张洪华, 吴宏鑫, 陈义庆.挠性卫星姿态的角动量反馈控制 [J].宇航学报, 2002, 23(3): 8-12.

ZHANG Honghua, WU Hongxin, CHEN Yiqing.Angular momentum feedback control for flexible spacecraft [J].Journal of Astronautics, 2002, 23(3): 8-12.

[4] 赵阳, 张大伟, 田浩.冗余飞轮姿控系统控制分配与重构研究 [J].空间控制技术与应用, 2010, 36(1): 1-6.

ZHAO Yang, ZHANG Dawei, TIAN Hao.Control allocation and reconfiguration of redundant wheels for spacecraft attitude control system [J].Aerospace Control and Application, 2010, 36(1): 1-6.

[5] 党朝辉, 项军华.超低轨卫星气动参数及转动惯量在轨实时辨识 [J].上海航天, 2012, 29(5): 20-24.

DANG Zhaohui, XIANG Junhua.Real-time identification of pneumatic parameters and inertia moment for ultra-low orbit satellite [J].Aerospace Shanghai, 2012, 29(5): 20-24.

[6] 刘军, 韩潮.挠性航天器大角度机动的振动抑制控制 [J].系统仿真学报, 2008, 20(7): 1880-1883.

LIU Jun, HAN Chao.Vibration suppression control of flexible spacecraft during large angle attitude maneuver [J].Journal of System Simulation, 2008, 20(7): 1880-1883.

[7] 陈雪芹, 张迎春, 耿云海, 等.基于控制有效性因子的卫星姿态控制系统在轨重构容错控制 [J].宇航学报, 2007, 28(1): 94-98.

CHEN Xueqin, ZHANG Yingchun, CENG Yunhai, et al.Satellite attitude control system on-orbit reconfigurable fault-tolerant control based on the control effectiveness factor [J].Journal of Astronautics, 2007, 28(1): 94-98.

[8] ZHANG J R, RACHID A, ZHANG Y.Attitude control for part actuator failure of agile small satellite [J].Acta Mechanica Sinica, 2008, 24(3): 463-468.

[9] 宗红, 张洪华, 徐福祥.受扰挠性卫星角动量反馈控制 [J].航天控制, 2009, 27(6): 42-45.

ZONG Hong, ZHANG Honghua, XU Fuxiang.Angular momentum feedback control for disturbed flexible satellites [J].Aerospace Control, 2009, 27(6): 42-45.

[10]李明群, 魏春岭, 袁军.红外地球敏感器测量值修正算法及其应用研究 [J].空间控制技术与应用, 2008, 34(5): 26-30.

LI Mingqun, WEI Chunling, YUAN Jun.Correction algorithm and its application to measurement of a scanning infrared sensor [J].Aerospace Control and Application, 2008, 34(5): 26-30.

[11]曹成军, 别朝红, 王锡凡.蒙特卡洛法全周期抽样的研究 [J].西安交通大学学报, 2002, 36(4): 344-348.

CAO Chenjun, BIE Zhaohong, WANG Xifan.Studies on complete sampling for Monte Carlo simulation [J].Journal of Xi’an Jiaotong University, 2008, 34(5): 344-348.

(编辑 苗凌)

AngularMomentumFeedbackControlofSatelliteAttitudewithInfraredEarthSensorCorrection

SU Wei1,2,HONG Tao2,XU Chuan2,HAO Peijie2

(1.State Key Laboratory of Astronautic Dynamics, Xi’an 710043, China; 2.China Xi’an Satellite Control Center, Xi’an 710043, China)

An angular momentum feedback control strategy with infrared earth sensor correction is proposed to solve losing control for low earth orbit satellite attitude due to the lost angular velocity measurement for the fault of angular velocity gyroscope.According to the relation between the changing angular velocity and that of momentum wheel on satellite, the least squares correction model of angular momentum feedback control is established based on chord length of infrared earth sensor and the optimal control coefficients are sought out by Monte Carlo algorithm.Then the angular velocity can be obtained from satellite control devices, and the information of satellite with angular velocity gyroscope fault is continuously recovered to realize three-axis-stabilized attitude control finally.It provides a new way for satellite fault treatment in terms of control system recombination to prolong the service life of satellite.

angular momentum feedback; attitude control; least squares estimation method

2013-08-16。

苏威(1979—),男,工程师;洪涛(通信作者),男,高级工程师。

国家自然科学基金资助项目(61179010)。

时间:2014-02-21

10.7652/xjtuxb201404020

TN95

:A

:0253-987X(2014)04-0115-04

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140221.115.001.html