隔膜压缩机二指数母线膜腔型面设计及实验验证

李霁阳,赵晓华,贾晓晗,彭学院

(1.西安交通大学能源与动力工程学院, 710049, 西安; 2.北京京城压缩机有限公司, 100061, 北京)

隔膜压缩机二指数母线膜腔型面设计及实验验证

李霁阳1,赵晓华2,贾晓晗1,彭学院1

(1.西安交通大学能源与动力工程学院, 710049, 西安; 2.北京京城压缩机有限公司, 100061, 北京)

针对广泛使用的单指数母线膜腔型面进行了优化计算,分析了该型面的特点和不足,同时以增大膜腔容积、降低膜片应力为目标,提出了二指数母线膜腔型面。该二指数母线膜腔型面下的膜片径向应力峰值在膜片半径的中间及边缘处,这样可以避开与膜片中心区域附加应力叠加,使得膜片中心区域油侧和气侧面上的径向应力相同且均处于一个较低的水平。对比研究结果表明:在相同膜腔半径、相同膜片材料及膜片内应力均达到许用应力条件下,二指数母线膜腔容积相比单指数增大6.6%;在相同膜腔半径、相同膜腔容积及相同膜片材料情况下,二指数母线膜腔下膜片最大径向应力相比单指数降低10.0%,膜片中心区域最大径向应力降低11.8%。

隔膜压缩机;膜腔型面;薄板大挠度理论;应力

隔膜压缩机是一种完全无泄漏的容积式压缩机,特别适用于压缩稀有、贵重、易燃、有毒、腐蚀性气体和其他纯洁度要求极高的气体。由于隔膜式压缩机的特殊结构,其排气压力范围很广,可以从0.1～300MPa[1],因此隔膜式压缩机作为压缩机体系中的一个十分重要的品种,已被广泛用于食品、医药、化工、石油、原子、国防等许多部门[2-3]。

隔膜压缩机的膜腔型面决定了压缩机的流量以及膜片的疲劳寿命。王迪生等提出采用双函数构造膜腔型面,使得膜片应力分布均匀性得到提高[4],但膜腔容积并未得到较大增长;班立兵利用数值迭代法对膜片贴合膜腔型面的变形过程进行了求解[5],并给出了基于传统膜腔型面的设计优化措施;吴波等利用Matlab优化工具箱对影响隔膜压缩机膜腔型面设计的主要参数进行了优化处理,并利用有限元方法求解了膜片内的应力分布[6-7],但并未对膜片破裂的原因进行详细讨论。此外,针对膜片寿命问题,Altukhov等认为排气阀孔的尺寸和放液压差是影响膜片寿命的重要因素[8];Kalshnikov等讨论了不同运行工况对膜片寿命的影响,并以此提出了粗略计算膜片寿命的方法[9];Ivanov提出了一种预估隔膜压缩机膜片可靠性的模型[10]。然而,以上研究多基于单指数母线型面[4],在此型面下膜片中心处是应力峰值区域,而型面中心区域的排气阀口也同时会对膜片产生附加应力,因此膜片中心处会呈现一种峰值应力和附加应力叠加的状态。为了防止膜片中心处应力过大,必须降低膜腔的最大挠度,所以这种型面下的膜腔容积较低。本文提出一种二指数母线膜腔型面,使得膜片的应力峰值从中心处向外转移,避开了与附加应力的叠加,因此膜腔容积有了显著提高。

1 膜腔型面设计理论

1.1 膜片变形理论

隔膜压缩机的基本结构如图1所示。当活塞达到上止点时,膜片下侧液压油压力达到最大值,膜片紧贴膜腔型面;随着活塞下行,膜片跟随液压油向下运动,膜腔容积增大,气体压力降低,开始进气;随着活塞运动至下止点,膜片与下支板部分贴合,进气结束;接着活塞开始上行并通过液压油推动膜片压缩气体;排气完成后膜片被液压油推动紧贴膜腔型面,完成一个工作循环。

隔膜压缩机在工作过程中膜片产生圆周对称变形,变形和应力都只是半径r的函数,并且由于隔膜压缩机在排气结束时液压油会推动膜片紧贴膜腔型面,使得膜片的应力达到最大值,因此本文研究的膜片应力均为膜片与膜腔型面紧密贴合时的应力。膜片的应力由拉伸应力和弯曲应力叠加得到,如图2所示。

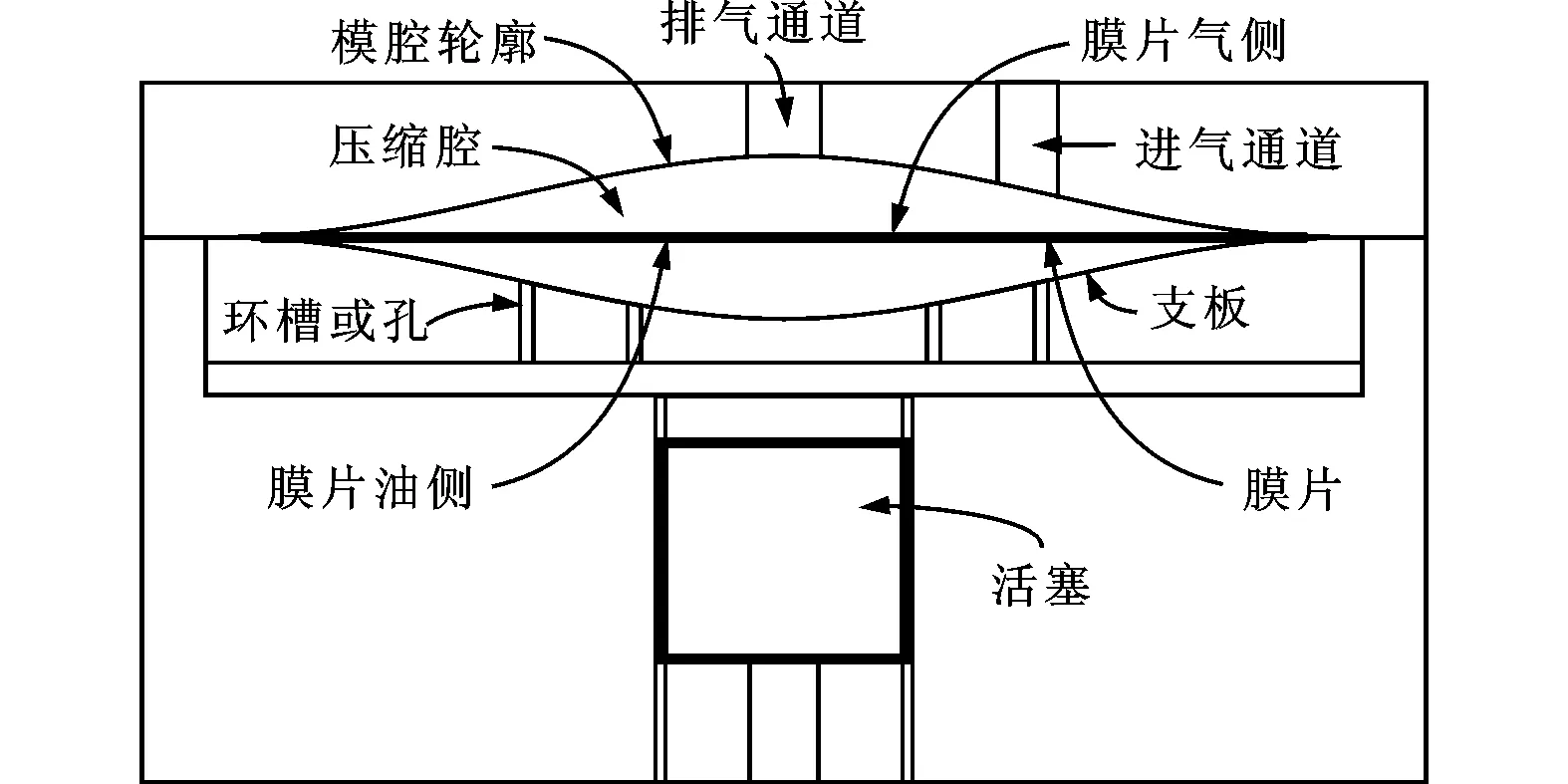
图1 隔膜压缩机结构

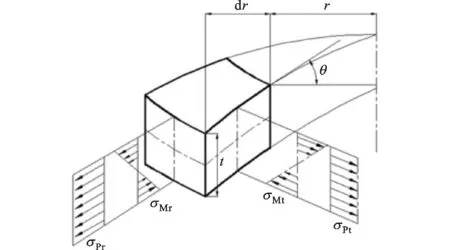
σPr为径向拉伸应力;σPt为周向拉伸应力;σMr为径向弯曲应力;σMt为周向弯曲应力;θ为膜腔型面的偏转角

4种应力可由下式求得[11]

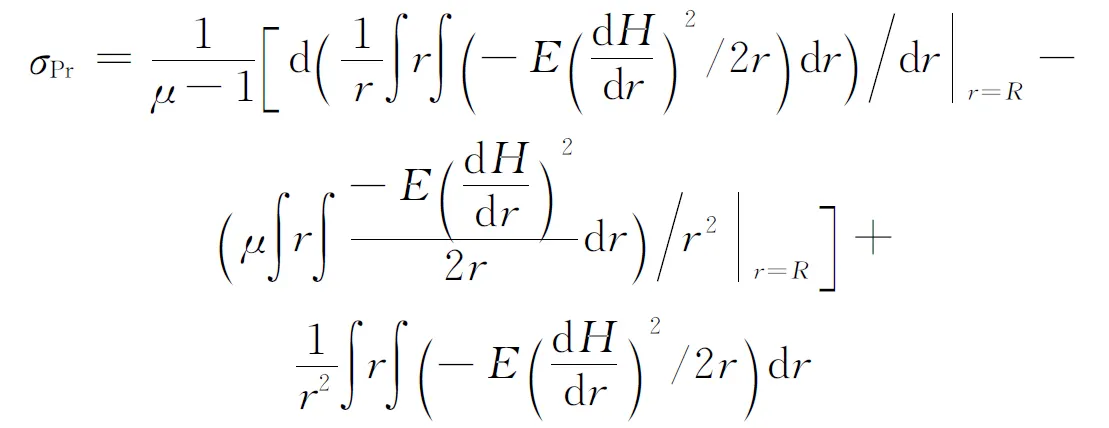
(1)

(2)

(3)

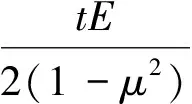
(4)

式中:t为膜片厚度;E为杨氏模量;μ为泊松比;H为膜片挠度,由膜腔型面确定。

如图2所示,弯曲应力在厚度方向的最大值在膜片的两侧,而拉伸应力在厚度方向上均布,因此膜片的应力极值位于膜片两侧。膜片气侧径向应力σGr、周向应力σGt、膜片油测径向应力σOr、周向应力σOt分别可以由下式计算

σGr=σPr-σMr;σOr=σPr+σMr

(5)

σGt=σPt-σMt;σOt=σPt+σMt

(6)

1.2 膜腔设计依据

隔膜压缩机膜腔型面为了防止膜片应力集中,必须满足以下几何条件[4]

(7)

式中:θ为膜腔型面的偏转角。

同时,膜腔型面还应该满足一定的应力条件。在使用单指数母线膜腔型面情况下,膜片的破裂位置普遍存在于3个位置,即膜片边缘位置、膜片中心位置以及支板最外圈环槽位置[12-13]。第1个破裂位置是在膜片径向应力最大处,而且裂纹成周向分布,即与径向应力垂直;第2个破裂位置为膜片径向应力峰值处,且承受排气阀孔引起的附加应力;第3个破裂位置是由于支板环槽的附加应力导致的,与膜腔型面几乎无关,故这里不做考虑。从前2处破裂位置可以看出,膜片内径向应力过大是导致膜片破裂的主要原因。马斯柯列夫也指出:径向应力应当作为膜片设计的决定因素,对于特定的膜片材料,当膜片紧贴膜腔型面时,膜片的径向应力σr不应超过许用径向应力[σa][2]。同时,考虑到膜腔中间的排气阀孔会对膜片产生附加应力,因此膜片中心区域的许用径向应力[σc]应低于膜片整体的许用应力[σa]。吸气阀对膜腔设计的影响一般不予考虑,这主要是因为在膜片向膜腔型面贴合的过程中,吸气阀处余隙容积内的气体来不及向膜腔中间流动从而导致吸气阀余隙容积内压力升高,与附加油压相平衡,进而避免了膜片在此处产生过大的附加应力,所以失效膜片在吸气阀口处几乎看不到附加变形,而在排气阀口处的附加变形很大。综上所述,膜腔型面设计应满足以下应力条件

(8)

式中:R1为最外圈排气阀孔包络圆的圆周半径。

2 膜腔型面优化设计

2.1 单指数母线膜腔型面优化计算

单指数母线膜腔型面的母线方程如下

(9)

式中:H0为膜腔中间处挠度;Z为挠度指数。本文以径向应力为设计准则,以表1中的膜腔及膜片基本参数进行单指数母线膜腔型面的优化计算,优化目标是在径向应力不超过许用应力的前提下膜腔容积达到最大。通过计算,当Z=8.8、H0=8.3时膜腔容积达到最大值974 cm3,此时膜片内径向应力分布如图3所示。

表1 基本设计参数

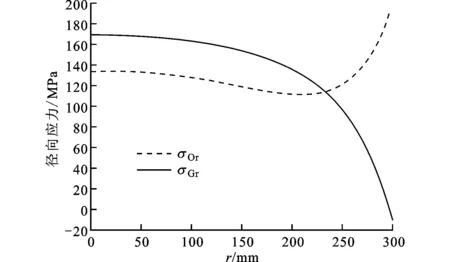
图3 单指数型面下膜片表面径向应力分布

从图3中可以看出,径向应力的峰值出现在膜片中间和边缘位置,这是单指数母线膜腔型面下膜片的应力分布特点。由于膜片中间要受到排气阀孔的附加应力,所以径向应力峰值出现在中间位置限制了膜腔容积的增大。如果将应力峰值从中间向周边移动,使其避开附加应力,那么膜腔容积将会增加。

2.2 二指数母线膜腔型面设计

在单指数母线膜腔型面中,母线的偏转角方程表示为

(10)

式中:C为待定常数。利用边界条件式(7)可推导得到单指数母线方程式(9)。利用式(2)可求得单指数母线膜腔型面下膜片径向弯曲应力

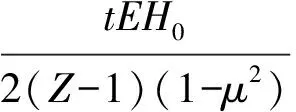
(11)

(12)

式中:n、m为指数;C为待定常数。利用上式及几何边界条件式(3),可得到二指数母线方程

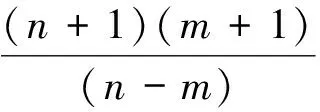
(13)

以表1中的膜腔及膜片基本参数进行优化计算可得,当n=3.1、m=3、H0=8.2时二指数母线膜腔容积达到最大值1 038 cm3,此时膜片表面径向应力分布如图4所示。二指数母线膜腔型面下膜片径向应力峰值在半径的中间处以及膜片的边缘处,避开了与膜片中心区域附加应力的叠加,并且在膜片中心区域油侧面和气侧面上的径向应力相同且均处于一个较低的水平。

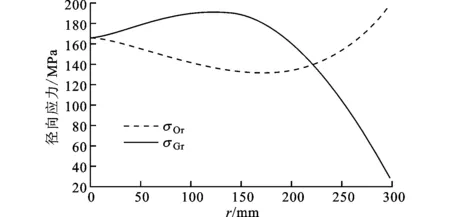
图4 二指数径向应力分布

3 实验验证

膜片内应力和应变的推导关系如下

(14)

式中:εr和εt分别为径向和周向相对应变量。

膜片表面径向应力可以通过测量膜片表面的径向及周向应变计算得到。本文搭建了隔膜压缩机膜片应变测试实验台,如图5所示。隔膜压缩机样机为V型双缸结构,2个气缸的膜腔型面分别按照二指数和单指数母线进行加工。为了防止应变片在隔膜压缩机工作过程中受到撞击,应变片黏贴在膜片油测。气缸中间位置(r=60mm)安装位移传感器,以检测膜片在气缸中的位置。

图5 实验装置图

3.1 二指数膜腔型面下膜片应力验证

膜腔型面母线方程为

(15)

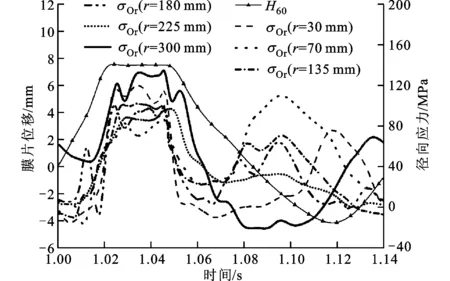
图6 周期内各测点径向应力及膜片位移

膜片油测在半径为30、70、135、180、225、300mm处沿径向及周向黏贴电阻应变片。隔膜压缩机吸气压力为大气压力,排气压力(表压)为0.5 MPa,最高油压(表压)为1.5 MPa。压缩机稳定工作时单个工作循环内膜片的位置及各个测点的径向应力及膜片位移H60如图6所示。在一个工作周期内,约有1/5时间膜片紧贴膜腔型面,此时各测点应力达到峰值并基本保持均匀。经过3次实验,当膜片紧贴膜腔型面时,各测点处的径向应力实验值与理论值的对比如图7所示。由图7可见,实验值与理论值趋势一致,但绝大部分实验值与理论值相比偏小,平均相对误差为12.3%。误差产生的主要原因是油压对应变片阻值的影响不能通过电阻补偿片完全消除。

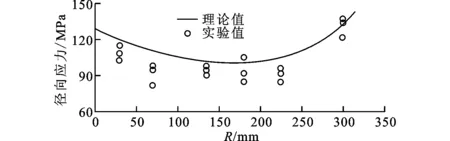
图7 各测点径向应力实验值与理论值对比

3.2 单指数膜腔型面下膜片应力验证

膜腔型面母线方程为

(16)

与二指数膜腔对应的支板结构不同,此膜腔型面对应支板为多孔结构,因此在膜片油测半径为30、90、220、280mm处沿径向及周向黏贴电阻应变片。压缩机运行工况与上文相同,稳定工作时单个工作循环内膜片的位置及各个测点的径向应力及膜片位移H60如图8所示。经过3次实验,当膜片紧贴膜腔型面时各测点处径向应力实验值与理论值的对比如图9所示。与3.1节实验结果类似,实验数据与理论值趋势一致,但绝大部分实验值偏小,平均相对误差为11.2%,误差形成原因与3.1节中的分析一致。

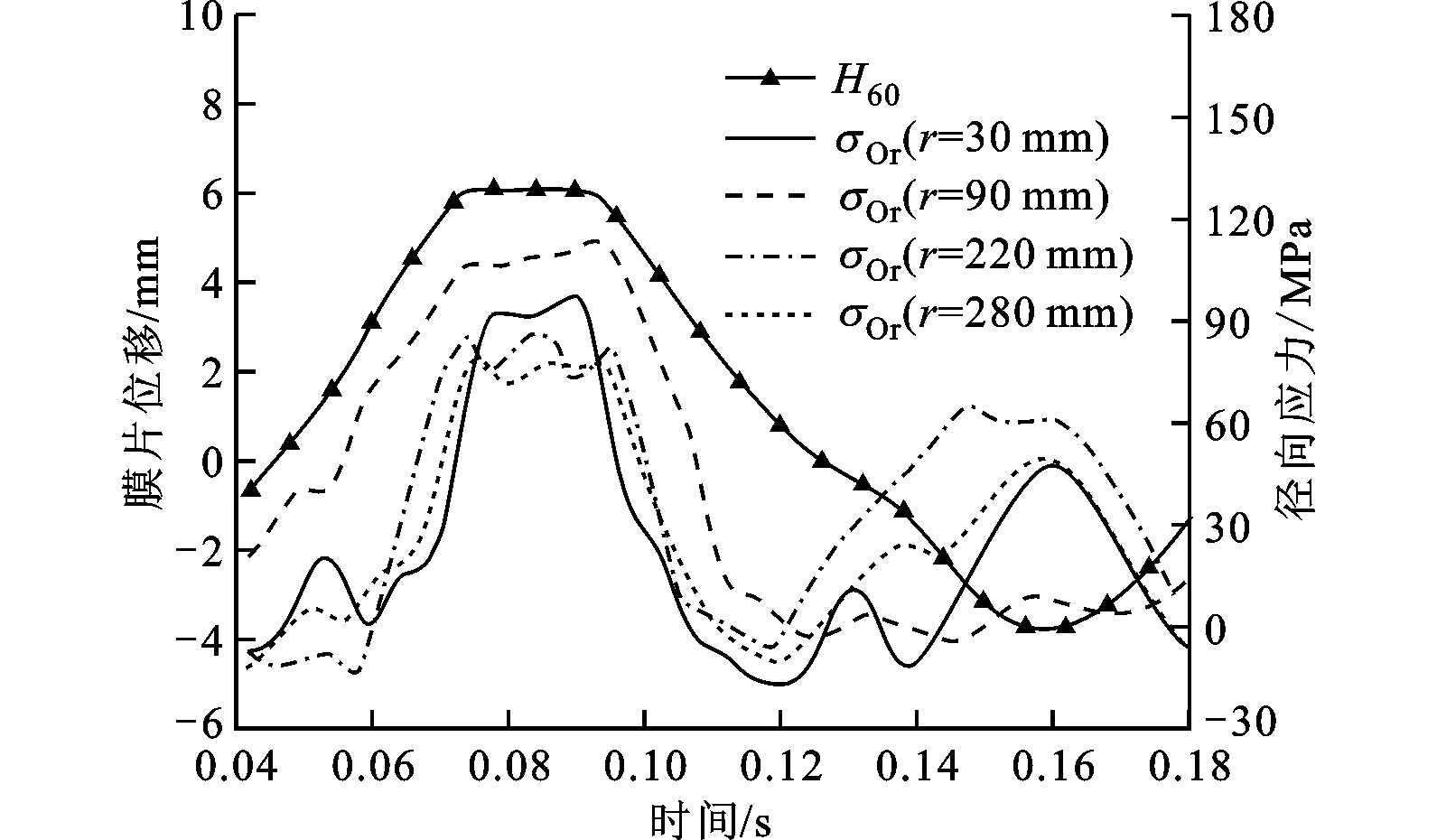
图8 周期内各测点径向应力及膜片位移

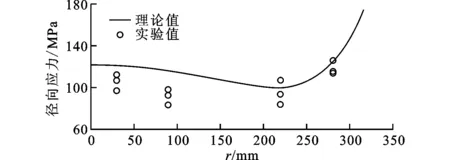
图9 各测点径向应力实验值与理论值对比

4 2种膜腔型面对比研究

膜腔容积以及膜片应力分布是衡量膜腔设计的2个主要标准。上文已利用实验验证了二指数及单指数母线膜腔型面设计理论的正确性,下面对单指数和二指数母线膜腔型面进行理论对比研究。

4.1 膜腔容积

在表1所示的典型隔膜压缩机设计参数下,对2种型面分别进行了优化计算,得到2种膜腔型面的母线形状如图10所示。从图中可以看出:单指数母线的最大挠度在膜腔型面的中心位置,随着膜腔半径增大,挠度迅速降低;二指数母线虽然最大挠度低于单指数母线,但随着膜腔半径增大,其挠度没有明显下降,因此二指数母线的膜腔容积大于单指数母线膜腔容积。计算结果表明,最优单指数母线膜腔容积为974 cm3,而最优二指数母线膜腔容积为1 038 cm3,二指数母线膜腔容积增长了6.6%。

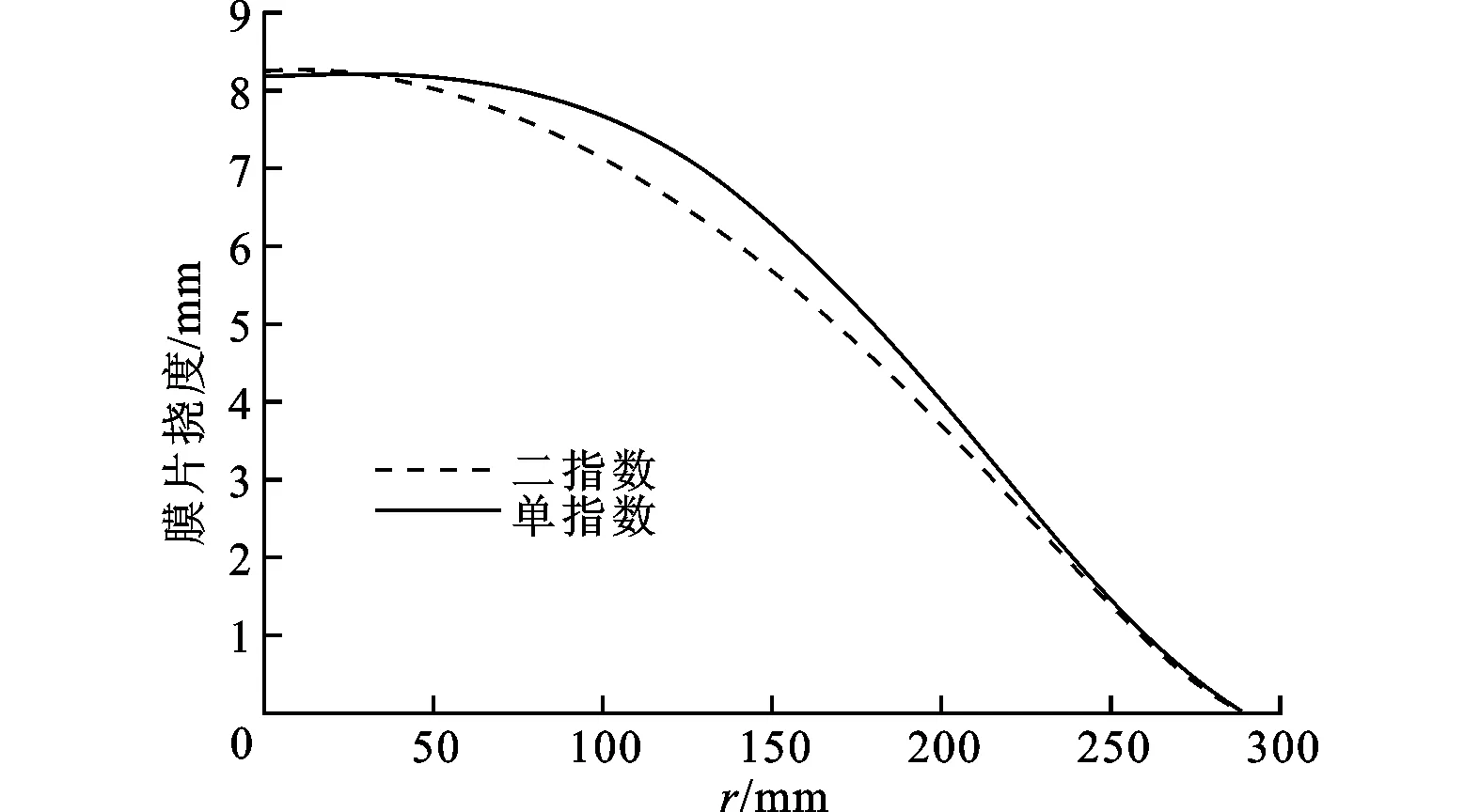
图10 2种不同膜腔型面母线形状

4.2 膜片应力

在相同膜腔容积下,利用二指数母线膜腔型面可以降低膜片径向应力最大值和膜片中心区域径向应力最大值。当膜腔容积同为974 cm3时2种膜腔型面下膜片径向应力分布对比如图11所示。2种膜腔型面下膜片最大径向应力都在膜片边缘处,在单指数母线膜腔型面下,膜片最大径向应力为200MPa,而在二指数母线膜腔型面下,最大径向应力则为180MPa,相比较最大径向应力下降了10.0%。膜片中心区域承受排气阀孔导致的附加应力,在长时间运行后排气阀孔处的膜片会发生塑性变形,因此膜片中心区域为破裂危险位置。在膜片中心区域,单指数母线膜腔型面下最大径向应力为169 MPa,而二指数母线膜腔型面下则为149 MPa,相比较单指数膜腔型面下降了11.8%。因此,在相同膜腔容积下,使用二指数母线膜腔型面可以降低膜片径向应力,从而提高膜片的寿命。

图11 2种膜腔相同容积下的膜片应力对比

5 总 结

本文针对隔膜压缩机膜腔设计特点,以径向应力不超过许用应力为设计原则,以薄板大挠度理论为基础,提出了一种新的二指数母线膜腔型面,并对单指数及二指数2种母线的设计理论进行了实验验证,得出以下主要结论:①提出了一种二指数母线膜腔型面,使得膜片径向应力最大值从膜片中心位置向外转移,解决了单指数母线膜腔型面下膜片径向应力最大值与中间排气阀孔附加应力相互叠加的问题;②对二指数及单指数母线膜腔型面下膜片油侧表面的径向应力进行了实验测定,验证了新老2种母线设计理论的准确性;③在相同膜腔半径、相同膜片材料及膜片内应力均达到许用应力条件下,二指数母线膜腔容积相比单指数母线膜腔容积增大6.6%;④在相同膜腔半径、相同膜腔容积及相同膜片材料情况下,二指数母线膜腔型面下膜片最大径向应力相比单指数降低10.0%,膜片中心区域最大径向应力降低11.8%。

[1] MANFRED D.Hofer diaphragm compressors [DB/OL].[2013-03-08].http:∥www.andreas-hofer.de/E/downloads/diaphragmcompressor10-02.pdf.

[2] 郁永章, 刘勇.特种压缩机 [M].北京: 机械工业出版社, 1989: 35-37.

[3] 徐文强.隔膜压缩机在HCNG站的运用 [J].产业与科技论坛, 2012, 11(6): 98-99.

XU Wenqiang.Application of diaphragm compressor in HCNG station [J].Industrial & Science Tribune, 2012, 11(6): 98-99.

[4] 王迪生, 冯海芃.隔膜压缩机双函数构造膜腔曲面 [J].西安交通大学学报, 1989, 23(3): 25-32.

WANG Disheng, FENG Haipeng.Design of diaphragm chamber curve surface shape with double function of a diaphragm compressor [J].Journal of Xi’an Jiaotong University, 1989, 23(3): 25-32.

[5] 班立兵.隔膜式压缩机膜腔曲面的优化研究 [D].北京: 中国科学院力学研究所, 1998.

[6] 吴波, 吴立志, 王兴国, 等.隔膜压缩机膜腔型线的分析研究 [J].压缩机技术, 2008(4): 1-4.

WU Bo, WU Lizhi, WANG Xingguo, et al.Analysis and study on the diaphragm cavity profile of diaphragm compressors [J].Compressor Technology, 2008(4): 1-4.

[7] 吴立志, 王兴国, 肖云锋.基于ABAQUS的隔膜压缩机膜片有限元分析 [J].北京石油化工学院学报, 2008, 16(4): 13-16.

WU Lizhi, WANG Xingguo, XIAO Yunfeng.FEM analysis with ABAQUS on the diaphragm in a diaphragm compressor [J].Journal of Beijing Institute of Petro-chemical Technology, 2008, 16(4): 13-16.

[8] ALTUKHOV S M, ZHUKOV A V.Determining the geometric parameters of the compression chamber of a diaphragm compressor with a hydraulic drive [J].Chemical and Petroleum Engineering, 1986, 22(7): 309-312.

[9] KALSHNIKOV V F, KUZNETSOV V D, ANTONOVA L I.Calculation of the reliability of a compressor diaphragm under variable loading [J].Chemical and Petroleum Engineering, 1987, 23(4): 168-170.

[10]IVANOV B A, NARKUNSKII S E, PLESHAKOV V F.Selection of materials for high pressure oxygen diaphragm compressors [J].Chemical and Petroleum Engineering, 1981, 17(6): 306-308.

[11]薛大为.板壳理论 [M].北京: 北京工业学院出版社, 1988: 81-91.

[12]顾惠君.隔膜压缩机典型故障分析 [J].煤炭技术, 2009, 28(10): 26-27.

GU Huijun.Typical fracture analysis of diaphragm compressor [J].Coal Technology, 2009, 28(10): 26-27.

[13]唐学敏.隔膜压缩机金属隔膜故障原因分析及对策 [J].机械, 2010, 37(S1): 77-78.

TANG Xuming.Analysis and treatment on the fracture of the diaphragm in the diaphragm compressor [J].Machinery, 2010, 37(S1): 77-78.

(编辑 刘杨 苗凌)

DesignandExperimentalVerificationforDiaphragmCompressorCavityProfilebyTwoExponentialTermsGeneratrix

LI Jiyang1,ZHAO Xiaohua2,JIA Xiaohan1,PENG Xueyuan1

(1.School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2.Beijing Jingcheng Compressor Co., Ltd., Beijing 100061, China)

The traditional generatrix of cavity profile is optimized and the characteristics of the traditional generatrix are discussed.A new generatrix of cavity profile of diaphragm compressor is presented for increasing cavity volume and decreasing diaphragm radial stress.With the new generatrix, the peak values of the diaphragm radial stresses occur in the middle of radius and edge, thus the radial stress in the diaphragm center gets lower.To verify the design theory for cavity profile, the radial stresses of the diaphragm oil side in the cavities with the new and traditional generatrices were tested, and the experimental radial stresses agree well with the theoretical ones.Additionally, the volumes of the cavities with different generatrices and the radial stress distribution of the diaphragm are theoretically analyzed.The results show that the cavity volume with the new generatrix is enlarged by 6.6% than that with the traditional generatrix under the same design conditions.The maximal radial stress in the cavity with the new generatrix decreases by 10.0% and the maximal radial stress in the centric region decreases by 11.8%.

diaphragm compressor; cavity profile; thin plate theory; stress

2013-07-17。

李霁阳(1990—),男,硕士生;贾晓晗(通信作者),男,博士,讲师。

国家科技重大专项资助项目(2012ZX06903012)。

时间:2014-01-20

10.7652/xjtuxb201404022

TH456

:A

:0253-987X(2014)04-0127-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140120.0843.002.html