基于高斯曲率识别板式无砟轨道中CA砂浆脱空伤损①

胡志鹏，王平，熊震威，代先星

(1.西南交通大学 土木工程学院，四川 成都 610031;2.西南交通大学高速铁路线路工程教育部重点实验室，四川 成都 610031)

CA砂浆作为板式无砟轨道结构的重要组成部分，其主要功能是作为调整层，提供板式轨道一定的弹性缓冲作用，其性能的好坏直接形响板式轨道应用的耐久性和维修工作。目前，我国高速铁路运营里程有万余公里，无砟轨道伤损也日显突出，其中CA砂浆伤损最严重，很有必要探索适合无砟轨道伤损检测的方法。由模态分析理论可知，伴随系统特性的改变必然导致模态参数的改变［1］，Pandey等［2－4］通过计算，研究了曲率模态的变化与损伤的关系，得出曲率模态是一个对伤损很敏感的参数。陈红等［5－8］用曲率模态及曲率模态差分析板式结构伤损，由于板式结构存在2个方向的曲率，何钦象等［9－10］提出用高斯曲率模态差识别结构伤损。由于轨道板－CA砂浆系统伤损前的数据很难得到，不容易计算出高斯曲率模态差。基于此原因，本文选择各阶模态下轨道板高斯曲率来识别CA砂浆的伤损。

1 理论背景

1.1 轨道板振动理论

由于轨道板的厚度比其长度和宽度小很多，轨道板在垂向可视为弹性薄板，根据弹性薄板理论，轨道板的垂向无阻尼自由振动方程可写为［11］:

式中:w1(x，y，t)为轨道板垂向挠度;hs为轨道板厚度;xFi，yFi为轨道板下第i个支撑点沿长度方向和宽度方向的坐标;E为轨道板弹性模量;NF是轨道板下离散支承点数;FsVi是轨道板下第i个支承点的垂向反力;ρs为轨道板密度;Ds为轨道板弯曲刚度。

在给定边界条件下，可以由式(2)解出振型函数W和相应的频率，利用初始条件可以求得轨道板在任一阶模态下的位移。

1.2 高斯曲率

在计算轨道板曲率模态时，会涉及x，y 2个方向的曲率模态值，由微分几何知识可知，高斯曲率可以综合反映板状结构2个方向上的曲率。设振型曲面［x，y，z(x，y)］上任一点的2个主曲率为 k1和k2，则其乘积称为曲面在这一点的高斯曲率，通常以 K 表示［12］。即

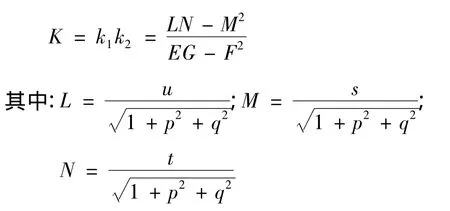
由于轨道板等间距划分，所以利用差分法分别计算 p，q，u，s，t的值。

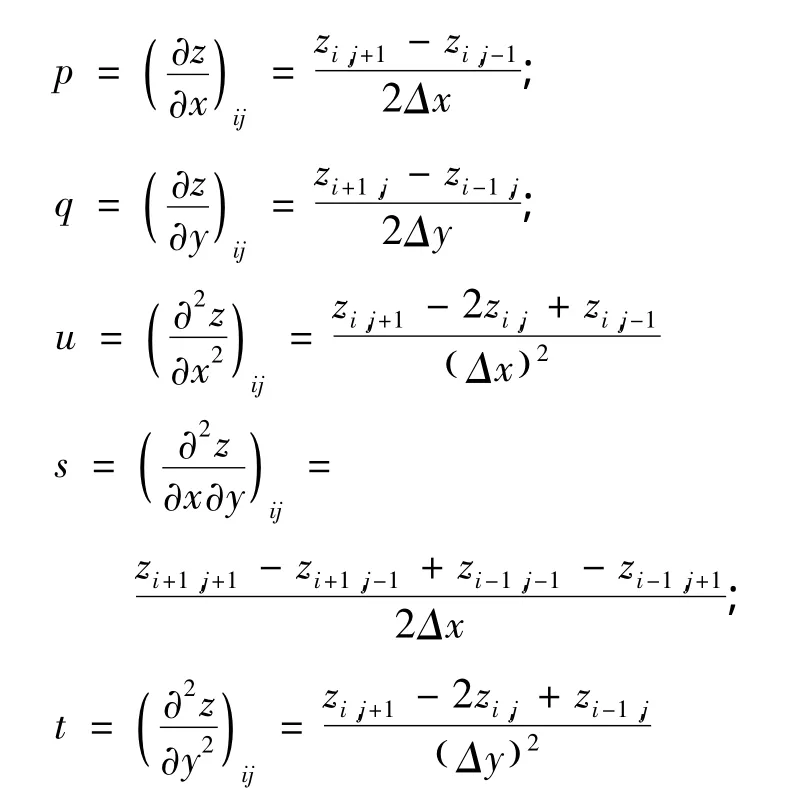
2 模型建立

利用有限元软件进行建模分析，建立轨道板－CA砂浆模型，轨道板采用shell63单元模拟，CA砂浆采用combin14弹簧单元模拟。轨道板参数为:弹性模量 E=3.65 ×1010Pa，密度为 2500 kg/m3，泊松比为0.2;砂浆 E=3×108Pa;轨道板长度4.8 m，宽 2.4 m。横向划分 12份，纵向划分 24份，轨道板四周采用全约束。模型中采用删除CA砂浆弹簧来模拟CA砂浆的脱空伤损，选取不同位置的砂浆脱空伤损进行计算分析。伤损工况如表1所示。

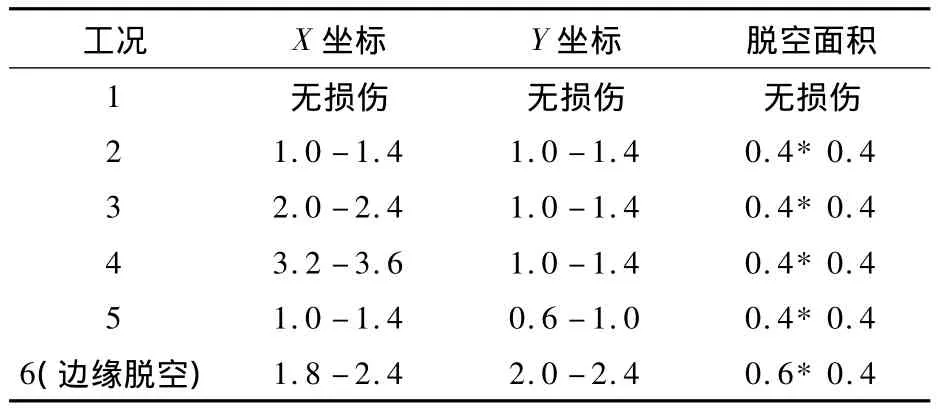
表1 CA砂浆脱空伤损Table 1 Void damage of CA mortar

2.1 基于固有频率识别CA砂浆脱空伤损

首先计算CA砂浆有损伤和无损伤时的固有频率，计算结果如表2所示。从前十阶计算结果中可以看出，只有第一阶固有频率变化幅度较大，其他阶固有频率变化很小，不能从固有频率的变化来准确识别伤损，只能作为一个初步判断的依据，为后续分析提供基础信息。

2.2 基于高斯曲率识别CA砂浆脱空伤损

2.2.1 轨道板－CA砂浆无伤损

通过对轨道板－CA砂浆模型的模态分析，计算出轨道板在各阶模态下的位移模态，利用高斯曲率理论识别CA砂浆的脱空伤损，考虑到以轨道板弯曲振动为主，本文只计算轨道板前五阶高斯曲率。通过编制matlab程序计算工况1和工况2的前五阶轨道板的高斯曲率，图1为工况1CA砂浆无脱空时的前五阶高斯曲率计算结果。

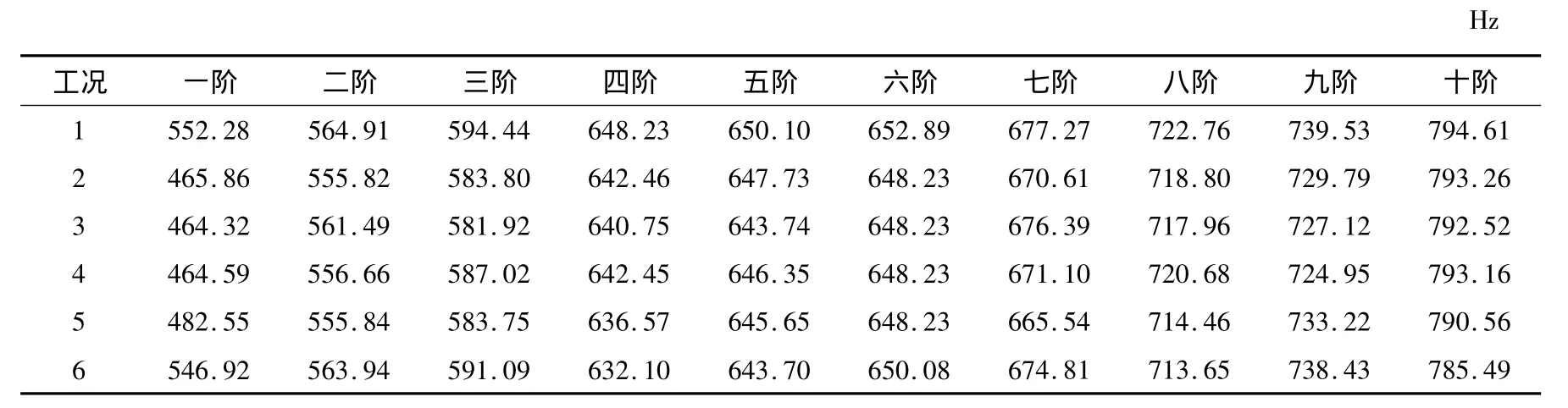
表2 轨道板－CA砂浆系统前十阶固有频率Table 2 First ten natural frequencies of the slab－CA motor system

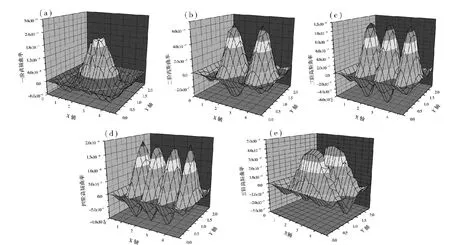
图1 工况1前五阶高斯曲率Fig.1 Working condition one of the first five order gaussian curvature

从计算结果可以看出，各阶模态下高斯曲率曲面平滑，轨道板高斯曲率形状与振型相对应，且没有出现明显尖峰，说明轨道板－CA砂浆系统没有伤损。

2.2.2 轨道板－CA砂浆有单处伤损

由于CA砂浆无伤损时计算了前五阶模态，工况2与之相对应也计算前五阶高斯曲率。工况2伤损模型如图2所示，计算结果如图3所示。

图2 CA砂浆脱空伤损模型Fig.2 Mode of the void damage of CA mortar

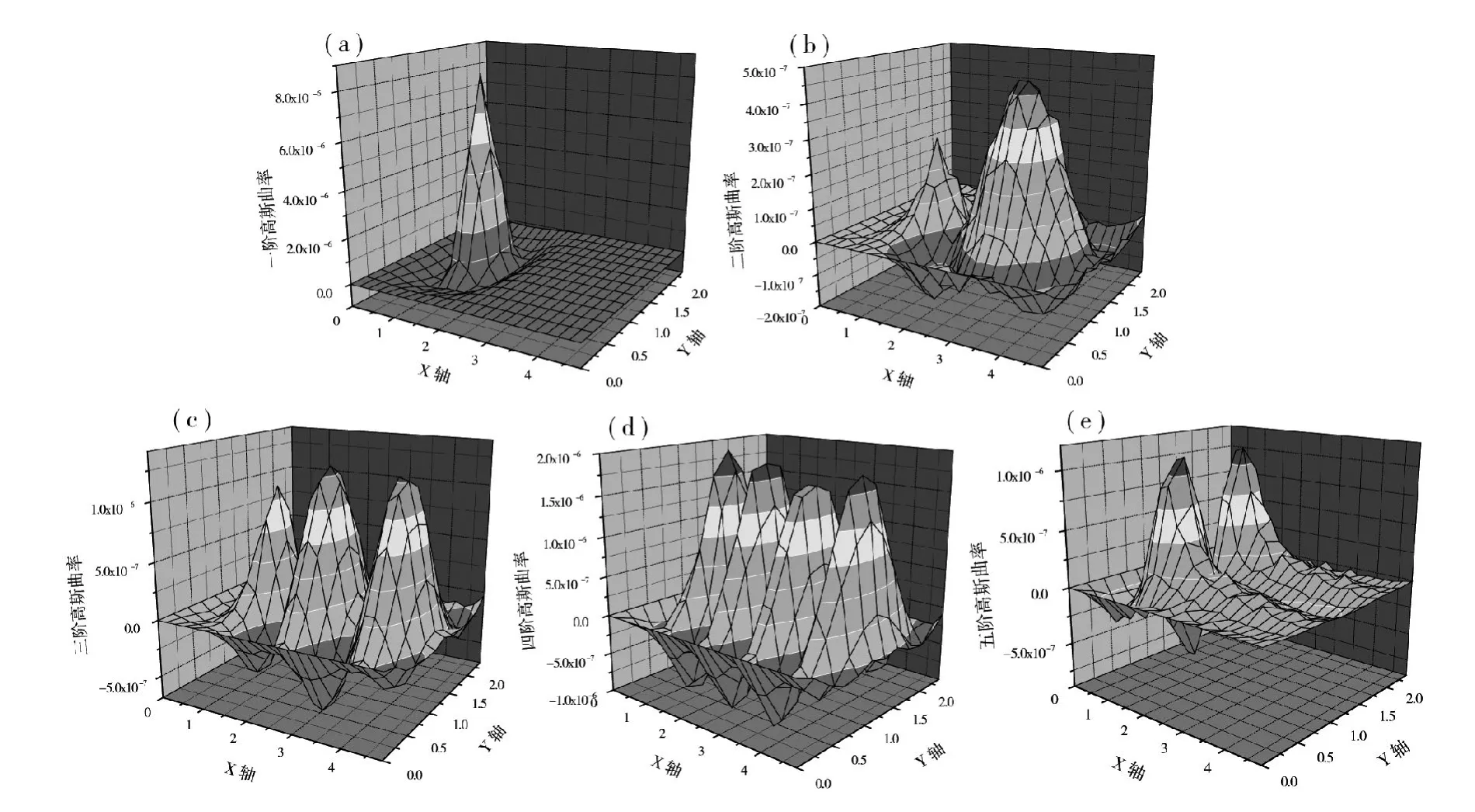
图3 工况2前五阶高斯曲率Fig.3 Working condition two of the first five order gaussian curvature

从轨道板前五阶高斯曲率计算结果来看，CA砂浆无损伤高斯曲率(图1中(a)～(e))与有损伤高斯曲率(图3中(a)～(e))有明显差异;其中第一阶、二阶、三阶高斯曲率在 X坐标:1.0～1.4，Y坐标:1.0～1.4区域内出现明显的尖峰，说明轨道板在该区域范围内曲率发生变化，进而可以判断出在该区域存在伤损。第四、五阶高斯曲率在X坐标:1.0～1.4，Y 坐标:1.0 ～1.4 区域内没有出现尖峰值，主要原因是该伤损处在这两阶模态的节线上，所以该方法对处在节线上的伤损识别存在不足，但可以综合前五阶模态结果来准确定位伤损的位置。

通过比较前五阶高斯曲率的计算结果，其中第一阶高斯曲率结果最明显，不仅能直观的判断轨道板－CA砂浆系统存在伤损，而且还可以准确识别伤损的位置。基于此，工况3至工况6只计算轨道板第一阶高斯曲率，其中工况6模拟CA砂浆边缘脱空伤损，并且在损伤处轨道板不施加约束。其计算结果如图4～图7所示。

从图4～图6可以明显看出，3种工况下的一阶高斯曲率分别在不同位置处出现尖峰，出现尖峰的区域与CA砂浆脱空的区域相一致，这说明一阶高斯曲率可以很准确的识别出伤损位置，识别效果很好。图7为CA砂浆边缘脱空，由于在脱空区域轨道板也不施加约束，一阶高斯曲率图中在边缘区域出现较小尖峰，出现位置与CA砂浆脱空区域一致。

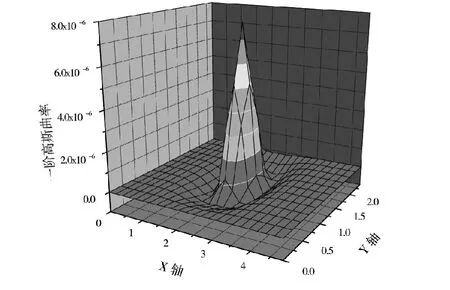
图4 工况3一阶高斯曲率Fig.4 Working condition three of the first order gaussian curvature

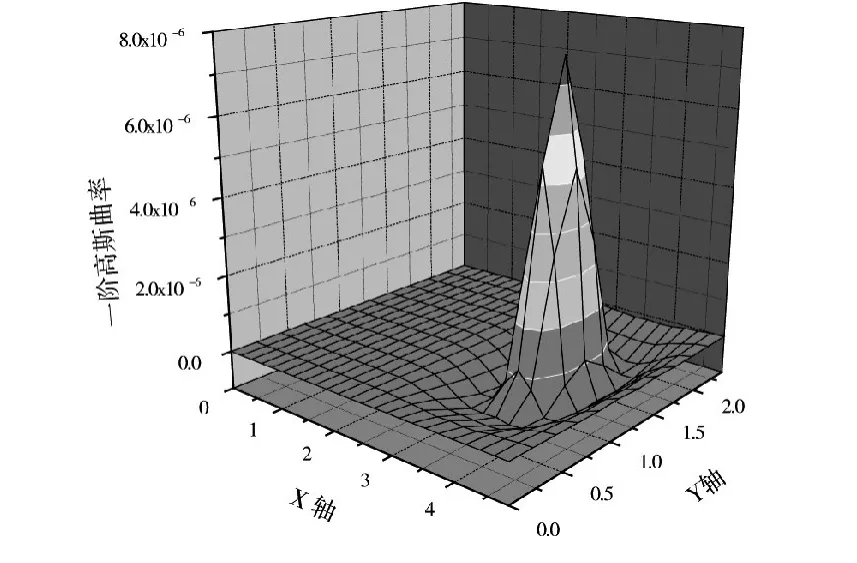
图5 工况4一阶高斯曲率Fig.5 Working condition four of the first order gaussian curvature

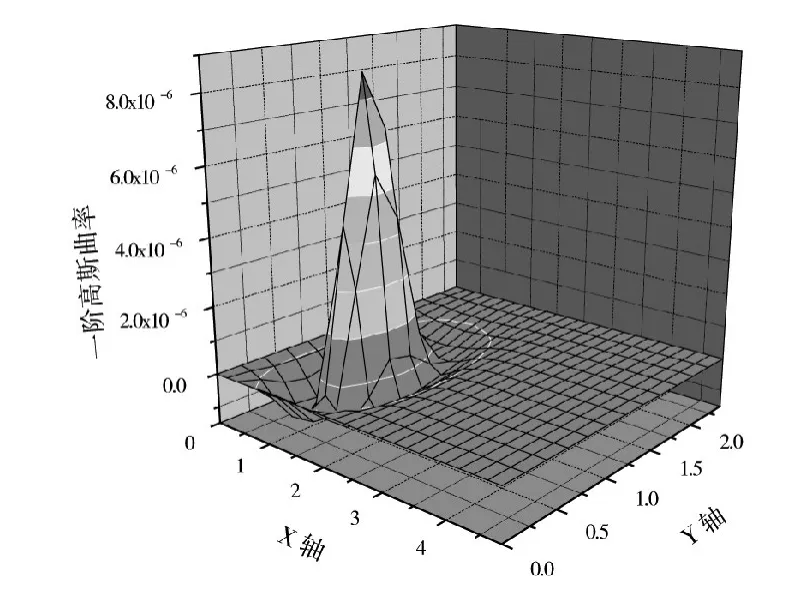
图6 工况5一阶高斯曲率Fig.6 Working condition five of the first order gaussian curvature

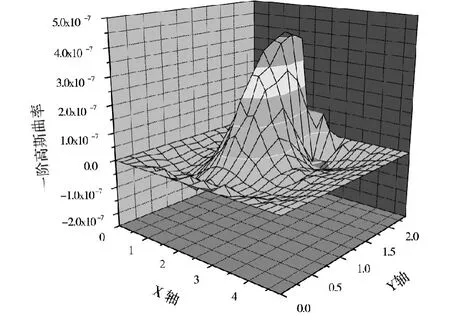
图7 工况6一阶高斯曲率Fig.7 Working condition six of the first order gaussian curvature

2.2.3 轨道板－CA砂浆有多处伤损

由CA砂浆单处伤损的计算结果和结论可知，利用轨道板第一阶高斯曲率就可以准确识别出伤损位置，针对CA砂浆在运营过程中难免存在多处伤损的现状，建立CA砂浆多处伤损有限元模型，如图8所示。并分析其第一阶高斯曲率，计算结果如图9。

图8 CA砂浆多处伤损模型图Fig.8 Mode of several void damages of CA mortar

由图8和图9可以看出，两处伤损面积虽一样大，但一阶高斯曲率值有差异，这是因为高斯曲率大的一处伤损处在一阶模态位移模态较大处，其曲率相对也较大。图9中2处尖峰位置即为伤损位置，与预设伤损位置一致，这说明一阶高斯曲率不仅可以准确识别单处CA砂浆伤损，还可以准确识别出多处伤损。

3 结论

(1)轨道板的前五阶高斯曲率可以反映伤损的有无及其具体位置，因此计算分析时只分析前五阶模态即可。

(2)轨道板的前五阶高斯曲率中，一阶高斯曲率最明显，对不同位置的CA砂浆脱空识别效果很好。如果一阶高斯曲率不能明显反应出伤损位置时，可以结合前五阶高斯曲率进行综合判断，准确定位出伤损位置。

(3)轨道板－CA砂浆系统一阶高斯曲率不仅可以准确识别单处CA砂浆伤损，还可以准确识别出多处CA砂浆伤损。

［1］李德葆，陆秋海，秦权.承弯结构的曲率模态分析［J］.清华大学学报，2002，42(2):224 －227.LI Debao，LU Qiuhai，QIN Quan.The curvature modal analysis of the bending structure［J］.Journal of Tsinghua University，2002，42(2):224 －227.

［2］Pandey A K，Biswas M，Samman M.Damage detection from changes in curvature mode shapes［J］.Journal of Soundand Vibration，1991，145(2):321 －332.

［3］杜金龙，郭少华.损伤梁动力特性的空间有限元分析［J］.铁道科学与工程学报，2008，5(2):17 －22.DU Jinlong，GUO Shaohua.The finite element analysis of dynamic characteristics of the damaged beam space ［J］.Journal of Railway Science and Engineering，2008，5(2):17－22.

［4］王学广，许艳英.基于高精度模态应变能法检测结构损伤的研究［J］.铁道科学与工程学报，2005，27(5):92－95.WANG Xueguang，XU Yanying.Effective structural damage detection method based on modal strain energy［J］.Journal of Railway Science and Engineering，2005，27(5):92－95.

［5］陈江，熊峰.基于曲率模态振型的损伤识别方法研究［J］.武汉理工大学学报，2007，29(3):99 －102.CHEN Jiang，XIONG Feng.Damage identification method based on curvature modal vibration mode［J］.Journal of Wuhan University of Technology，2007，29(3):99 －102.

［6］李国强，梁远森.振型曲率在板类结构动力检测中的应用［J］.振动、测试与诊断，2004，24(2):111 －116.LI Guoqiang，LIANG Yuansen.Modal curvature in the application of plate type structure dynamic test［J］.Journal of Vibration，Measurement ＆ Diagnosis，2004，24(2):111－116.

［7］张波，王赟，姜峰.基于曲率模态差的四边固支薄板的损伤检测［J］.河北工程大学学报(自然科学版)，2009，26(3):31 －36.ZHAGN Bo，WANG Yun，JIANG Feng.Damage detection for elastic thin plate with fou r simply clamped edges based on curvature model difference［J］.Journal of Hebei University of Engineering(Natural Science Edition)，2009，26(3):31 －36.

［8］白羽.梁－板－网架结构损伤诊断研究［D］.昆明:昆明理工大学，2008:28－33.BAI Yu.The damage detection research of bridge－plate－space truss structure［D］.Kunming:Kunming University of Science，2008:28 －33.

［9］何钦象，杨智春，姜峰，等.薄板损伤检测的高斯曲率模态差方法［J］.振动与冲击，2010，29(7):112 －115.HE Qinxiang，YANG Zhichun，JIANG Feng，et al.The damage detection method of thin plate gaussian curvature mode difference［J］.Journal of Vibration and Shock，2010，29(7):112 －115.

［10］韩西，李庆达.基于高斯曲率模态差的T梁结构二维损伤识别研究［J］.重庆交通大学学报(自然科学版)，2012，31(4):747 －750.HAN Xi，LI Qingda.The T－bridge structure of two－dimensional damage identification research based on aussian curvature mode difference［J］. Journalof Chongqing Jiaotong University(Natural Science Edition)，2012，31(4):747 －750.

［11］刘学毅，赵坪锐，杨荣山，等.客运专线无砟轨道设计理论与方法［M］.成都:西南交通大学出版社，2010:56－85.LIU Xueyi，ZHAO Pingrui，YANG Rongshan，et al.The design theory and methods of Passenger railway ballastless track［M］.Chengdu:Southwest Jiaotong University press，2010:56 －85.

［12］周振荣，杨文茂，郑高峰.微分几何［M］.武汉:武汉大学出版社，2008:49－58.ZHOU Zhenrong，YANG Wenmao，ZHENG Gaofeng.Differential geometry［M］.Wuhan:Wuhan University Press，2008:49 －58.