基于频率法的平行钢绞线索索力测试研究①

孙增寿，赵云鹏，秦磊

(郑州大学土木工程学院，河南 郑州 450001)

在工程实践中，频率法以其操作简单、使用方便、仪器可重复使用且测量结果准确等优势而被广泛地应用于成品拉索索力测试［1－6］。而对于平行钢绞线索，需在现场对索中钢绞线进行逐根张拉以达到整索的设计索力或成桥索力［7］，在张拉过程中，由于人工控制张拉设备的误差和温度变化等原因，会导致各钢绞线的张拉力存在一定程度的偏差，进而导致实际索力和设计成桥索力存在偏差，这就需要实测所建立的索力大小。另外，桥梁在使用一段时间后，由于锚具松动，或腐蚀断丝，索力降低，也需要对索力进行测试［8－9］。但是，用频率法测试平行钢绞线索的索力时，由于钢绞线之间相互分散，索中间部分区域由于垂度作用会有所接触，因此，各钢绞线在独立振动的同时又相互干扰。为此，本文以实际桥梁斜拉索为例，对基于频率法的平行钢绞线索的索力测试问题进行分析研究。

1 拉索中钢绞线张拉力的不均匀与钢绞线离散性分析

光武大桥为一2联2×80 m的双索面斜拉桥，每联12对斜拉索。选取斜拉索中的3根索进行分析，索的物理参数如表1所示。

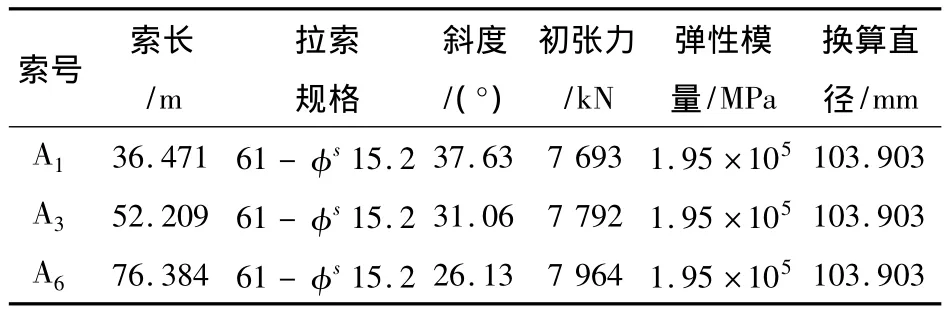
表1 斜拉索物理参数Table 1 Physical parameters of the stay cables

《公路斜拉桥设计细则》第8.3.3条规定:斜拉索张拉完成后的索力与设计值之间的误差不能大于5%;对于平行钢绞线斜拉索，索内各根钢绞线的张拉力差值应控制在2% ～8%［10］。为此，考虑单根钢绞线的张拉力偏差，分别采用索力偏差为±5%，±3%和±2%来选定各根拉索的索力，使用结构分析软件Midas/civil分别建立单根钢绞线、多根钢绞线索的接触耦合模型进行分析计算。假设索由7根钢绞线组成，截面如图1所示，各钢绞线的索力取值如表2所示。

图1 7根钢绞线布置截面示意图Fig.1 Schematic section of 7 steel stranded wires

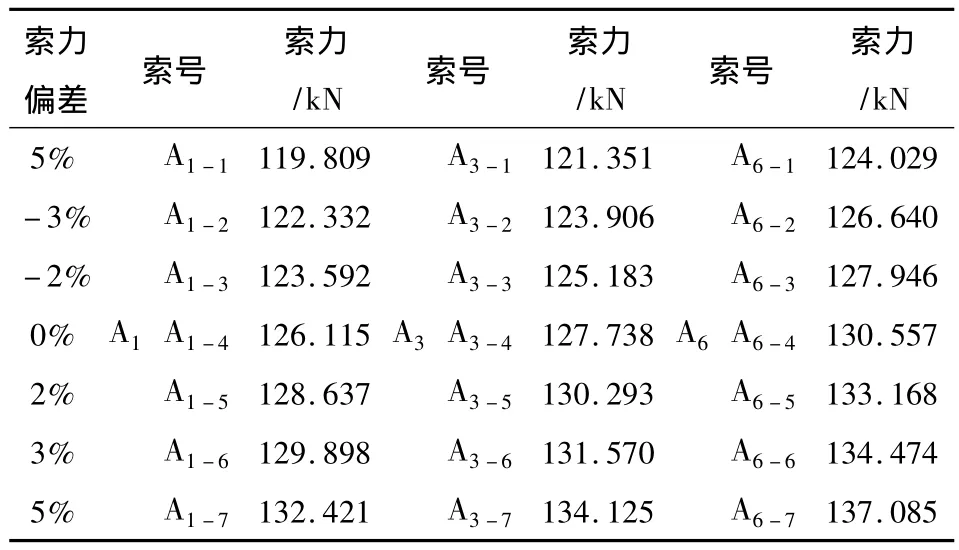
表2 索力不均匀性取值Table 2 Non uniformity of cable tensions

在平行钢绞线索中，由于各根钢绞线之间索力的不均匀性以及拉索自重的作用，各根钢绞线会产生不同的垂度，钢绞线在拉索中间部分区域会发生接触，而在其余位置则相互分散［11－13］。另外，在实际工程中，钢绞线外侧一般都采用热挤PE防护套，使各根钢绞线之间存在很大的摩擦，切向滑移变形很小或者不滑移，因此，在分析建模中，索中钢绞线之间的实际接触情况更接近于弹性连接中的刚性连接。

在实际平行钢绞线索桥梁中，由于索体外包HDPE套管，各根钢绞线之间的接触区域无法测得，因此，在建模中采用逐步扩大接触区域的方法来模拟各根钢绞线之间的接触，分别建立耦合中间两点、耦合中间1/5区域、耦合中间1/3区域、耦合中间1/2区域、耦合中间2/3区域的分析模型，对比不同接触区域情况下索自振频率的变化情况。分析模型如图2和图3所示。

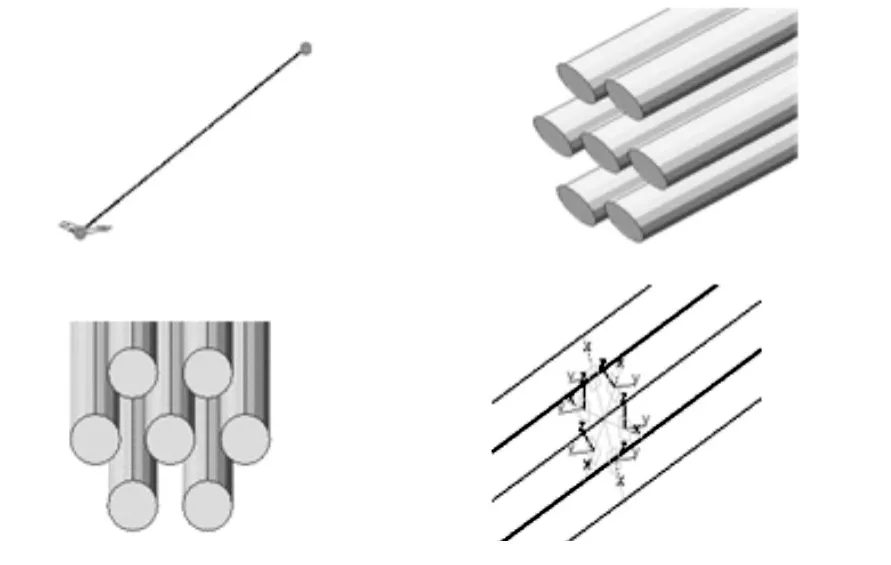
图2 A1－7钢绞线接触模型Fig.2 Contact model of 7 steel stranded wire of A1cable

用刚性连接模拟索中钢绞线之间的接触时，拉索振动频率如表3所示，表中列出了不同接触范围情况下拉索的前6阶振动频率，分析表3数据可以看出:

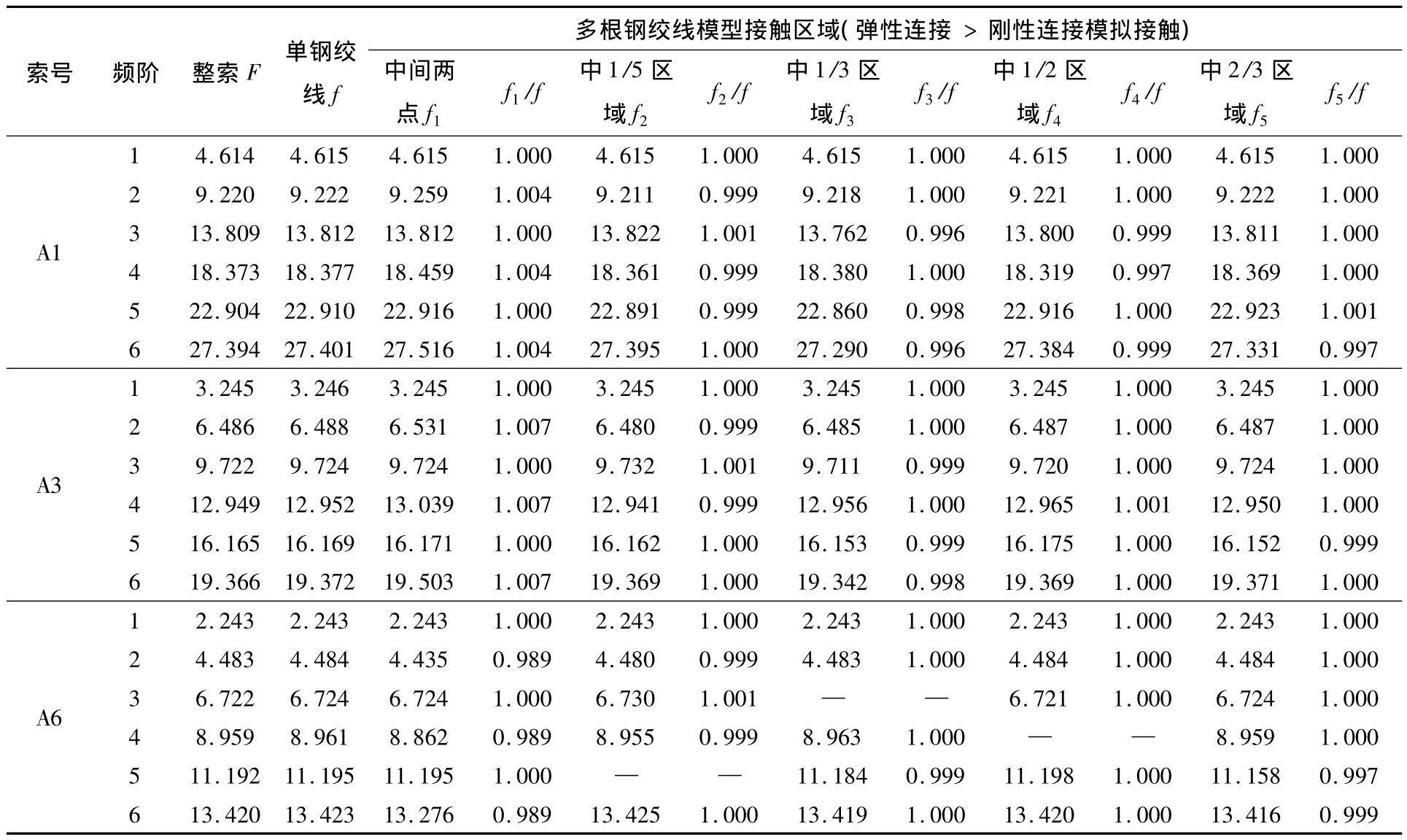
表3 不同接触区域各拉索的振动频率表Table 3 Vibration frequency of every cable contacted in different area Hz

图3 钢绞线之间接触区域详图Fig.3 The contact area details of steel stranded wire

(1)单根钢绞线的振动频率与整索的振动频率基本一致，尤其是一阶振动频率;但随着频率阶数的提高，两者之间的误差有所增大，不过随索长增加，这一误差越来越小，可忽略不计。

(2)随钢绞线中间部分接触区域的增大，索的振动频率值变化很小。

(3)索中钢绞线只有中间2点接触时，拉索的接触区域较小，在对称振型时各钢绞线同时振动，频率值与单根钢绞线相同;在反对称振型时，各钢绞线之间在独立振动的同时又相互干扰，振动频率存在误差，但最大误差仅1.1%。

(4)上述结论也适用于其他桥中的斜拉索。

以索中钢绞线中间1/5区域耦合的A6索为例，其前四阶振型如图4所示。从图4可以看出，当多根钢绞线之间切向不能自由滑移时，各根钢绞线基本上可以同时起振，相当于单根钢绞线，振动形态规整。

从以上分析讨论可知，对于平行钢绞线斜拉索，索力不均匀以及各钢绞线之间的离散对测量频率的影响较小，采用频率法来测量平行钢绞线索的索力是可行的。

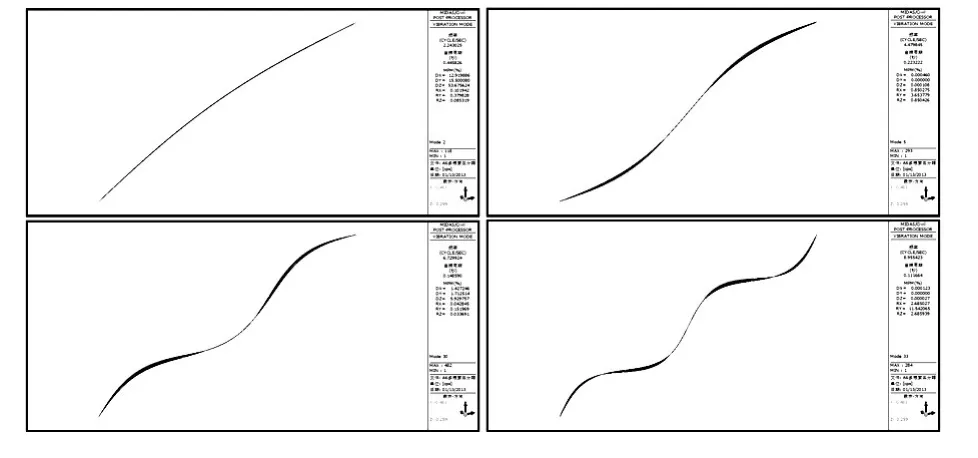
图4 A6索中间1/5区域耦合的前四阶振型Fig.4 First four modes of A6cable coupled in middle 1/5

2 拉索外包HDPE套管对频率法测试的影响

在索承式桥梁中，为了延长拉索的使用寿命，平行钢绞线索常采用多层防腐体系，即高强钢丝环氧涂层、单根钢绞线外热挤PE护套和整个索体外安装耐腐蚀性能好的 HDPE 套管［11－12］。外包HDPE套管的直径比索体直径大很多，两者之间没有任何介质，只在两端与预埋套筒对接。HDPE套管因受力很小会在索中间区域直接搭在索体上。在用频率法测试拉索索力时，特别是在成桥之后，一般是将拾振器固定在索体外的HDPE套管上，那么索体振动能否传到套管上?套管能否和索体共同振动?以及HDPE套管对测试频率的影响等都需要进行研究，以判断频率法测量平行钢绞线索索力的准确性。

仍以A1，A3和A63根斜拉索为例进行分析，HDPE套管的各项参数如表4所示。相对索体而言，外包HDPE套管的自重较轻，且套管两端受力很小，在建立其分析计算模型时，也用索单元进行模拟。经分析，HDPE套管的各阶振动频率如表5所示。从表5可以看出:HDPE套管的振动频率很小，而且随着索长的增加，其振动频率越来越小。

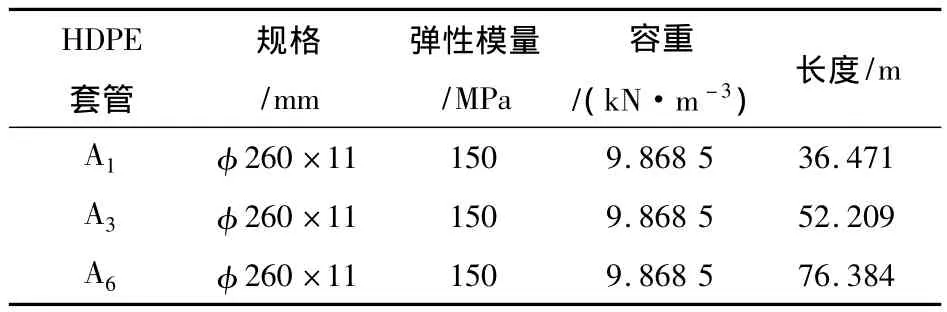
表4 HDPE套管参数Table 4 Parameters of HDPE casing

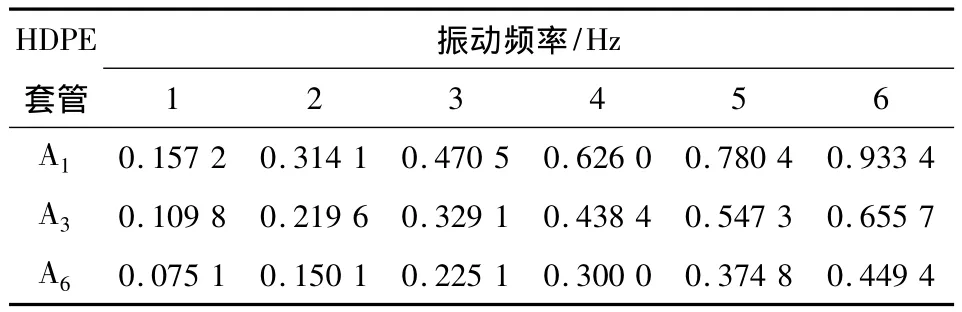
表5 HDPE套管振动频率Table 5 Vibration frequencies of HDPE casing

进一步建立索和套管的整体模型，研究HDPE套管对索体振动频率的影响。由于无法直接测得HDPE套管与索体的接触区域，所以在模型中仍然采用逐步扩大接触区域的方法来模拟接触，通过计算所得振动频率的对比来反映索体外包HDPE套管对拉索振动频率的影响。

同前，在模型中采用的接触区域分别为:中间两点接触、中间1/5区域接触、中间1/3区域接触、中间1/2区域接触、中间2/3区域接触、全部接触;索体与HDPE套管之间的接触采用弹性连接中的仅受压连接来模拟，轴向刚度取HDPE套管刚度1.5×105kN/m。以A6索为例，索和套管的整体模型如图5所示。对应不同接触区域，整体模型的振动频率如表6所示。从表6可以看出，随着接触区域的逐渐增大，拉索的各阶频率逐渐减小，说明HDPE套管对索体振动的影响逐渐增大，当中间2/3区域接触时，索体与HDPE套管组成的系统的振动频率与整索的振动频率相差3.5%左右，最大达4.9%。可见，HDPE套管对索体振动频率有一定影响，在索力测量过程中必须考虑这一因素。

图5 索和套管整体模型Fig.5 Overall model of cable and casing

以索和HDPE套管中间1/2区域耦合为例，套管－索体的前4阶振型如图6所示。从图6可以看出:索体本身的振动形态很规整，HDPE套管对索体振动形态的影响较小。且外包HDPE套管的重量较小，自振频率比拉索小很多。因此外包HDPE套管的振动基本上是由索体振动引起的强迫振动。

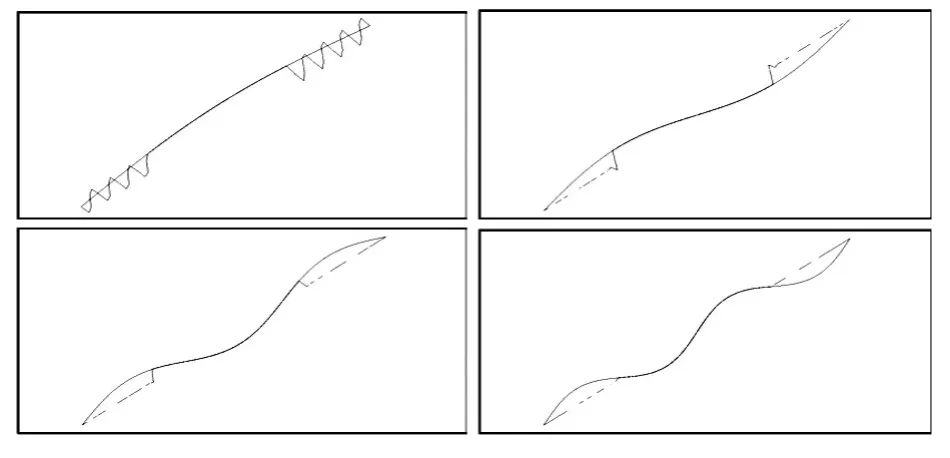
图6 索－套管系统中间1/2区域耦合情况下前四阶振型Fig.6 First four modes of cable－casing system coupled in middle 1/2

根据以往工程经验，HDPE套管与索体的接触区域一般在拉索长度的1/2以上，由表6可知，此时振动频率的误差较大，因此必须考虑HDPE套管的影响。HDPE套管由于自重作用会直接搭在索体上，所以可通过对拉索的线密度进行修正，以反映HDPE套管对索振动频率测试的影响。将HDPE套管质量换算计入索体线密度，换算后的索体线密度为75.48 kg/m。假定HDPE套管与索体全部接触建立分析计算模型，索体前6阶振动频率的计算结果如表7所示。

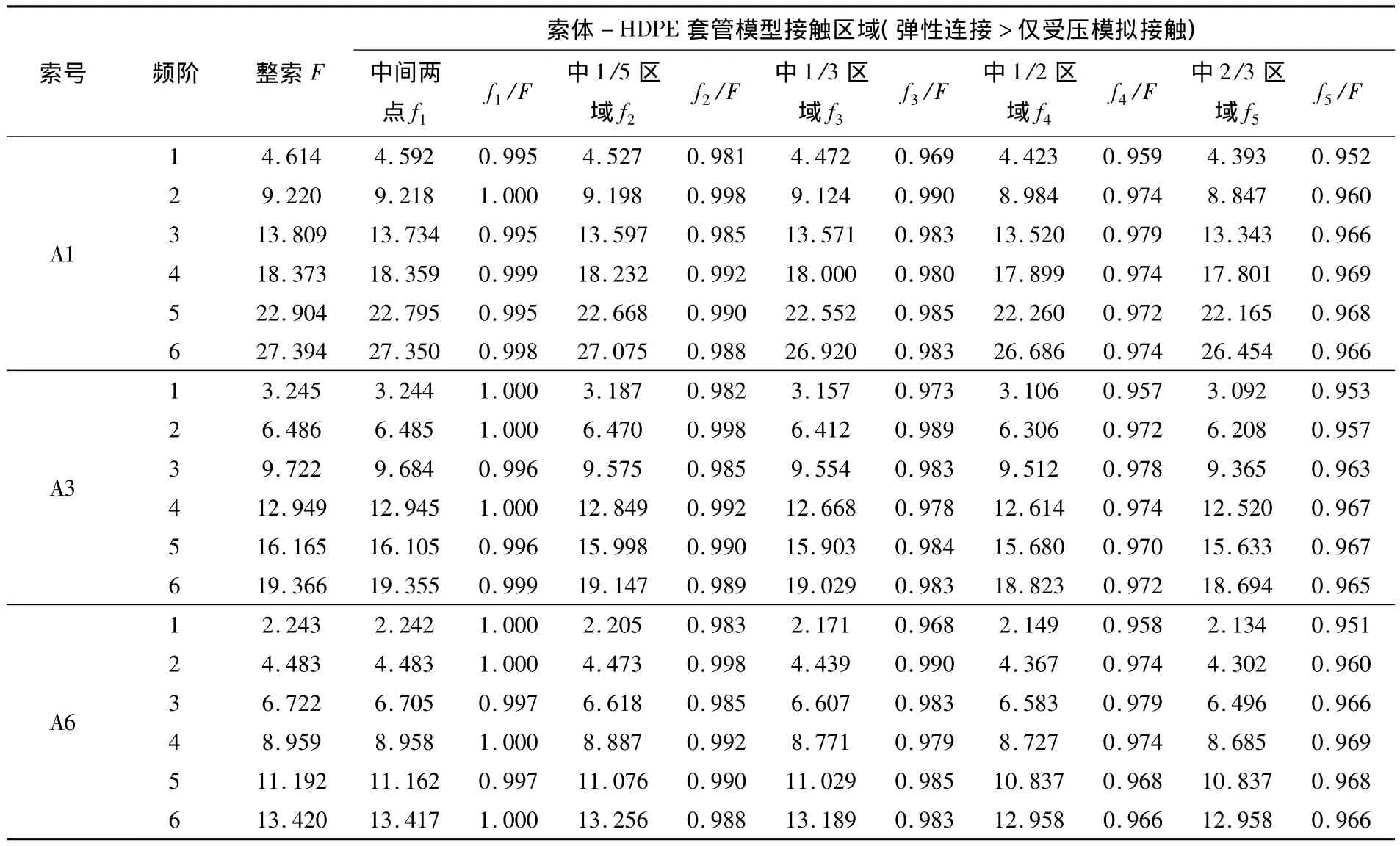
表6 考虑HDPE套管影响的拉索振动频率Table 6 Cable vibration frequencies considering effect of HDPE casing Hz

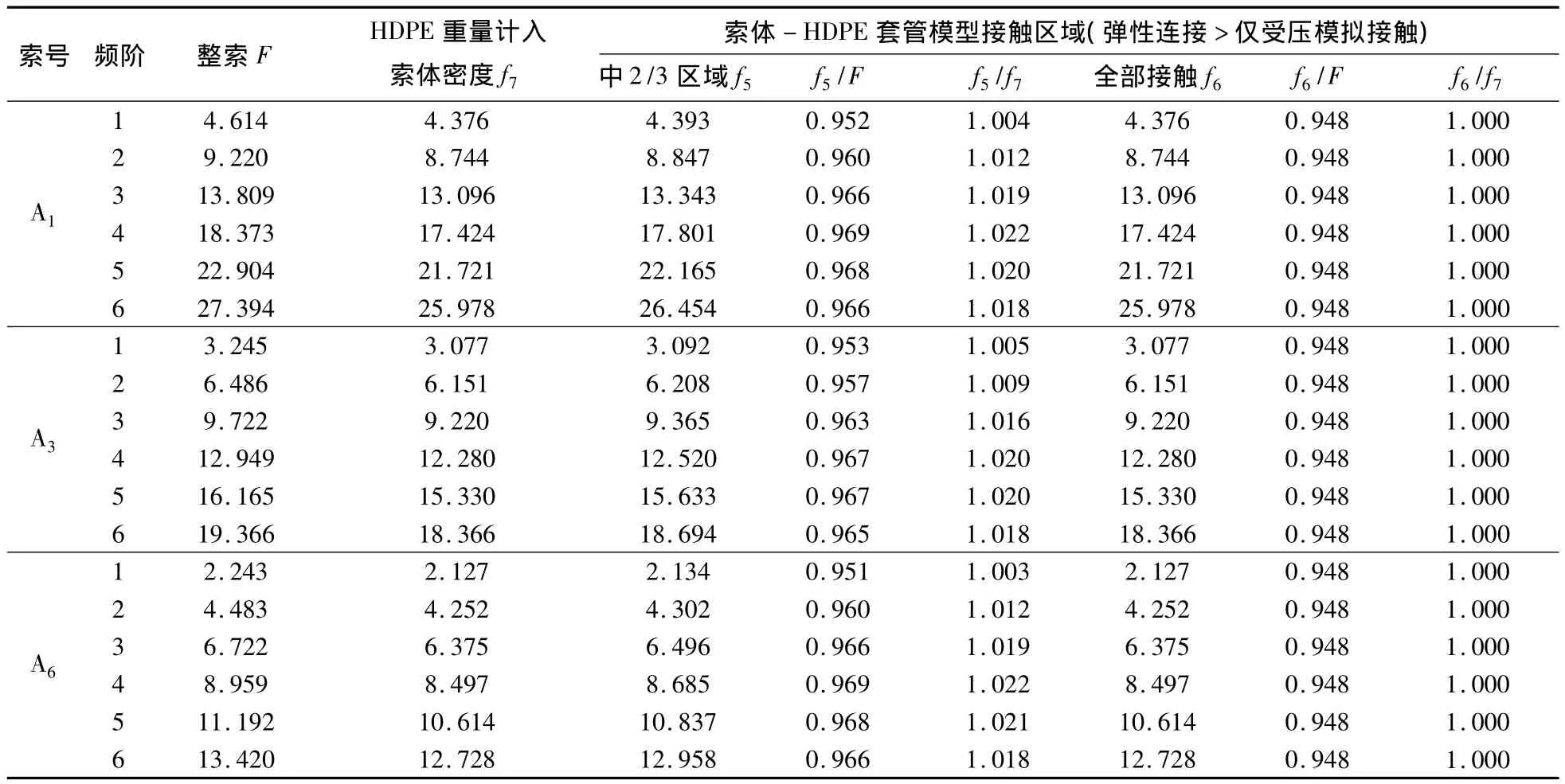
表7 索体线密度修正后的结果对比Table 7 Comparison of results considering linear density correction Hz

从表7可以看出:将HDPE套管质量换算计入索体线密度得到的索的各阶振动频率与索体和HDPE套管全接触时索的各阶振动频率基本相同，说明在实际桥梁索力测试中，可考虑对拉索的线密度进行修正。但是在实际桥梁中，HDPE套管与索体的接触区域往往在一半以上而没有达到全部接触，因此将HDPE套管质量直接计入索体线密度也不十分恰当，此时最大误差仍有2.2%，不过对拉索的一阶频率来说，误差却很小，只有5‰，符合索力测试精度要求，而且对使用平行钢绞线索斜拉桥，斜拉索的基频更容易激振和测量出来。

3 斜拉索索力测试试验

为了验证频率法能够用于平行钢绞线索索力测试，以及索力计算过程中需要考虑HDPE护套影响对索线密度进行修正，选取表1所示斜拉索进行索力测试，测试结果如表8所示。从试验结果可以看出，索力测量和计算精度较高，约提高4%左右的索力测量精度;同时，随斜拉索长度增大，振动法测试的频域波形图越清晰，测试结果越准确。

表8 索力测试结果Table 8 Measurement results of cable tensions

4 结论

(1)在平行钢绞线索桥梁中，可以采用频率法测量平行钢绞线拉索的索力;

(2)HDPE套管能够传递和反映内部索体的振动，但在索力测试和计算时，须根据套管的质量对斜拉索的线密度进行修正，可提高4%左右的索力测量精度;

(3)在识别和确定斜拉索基频时，尽量选用斜拉索振动信号的第一阶频率，保证频率法测量斜拉索索力的精度。

［1］卢尧，王金枝，陈小佳.频率法测定拉索索力的研究［J］.交通科技，2007(2):17 －19.LU Yao，WANG Jinzhi，CHEN Xiaojia.Study of the measurement of cable tension by frequency method［J］.Transportation Science and Technology，2007(2):17 －19.

［2］董建华.中、下承式拱桥吊索的模态分析与张力测定［D］.郑州:郑州大学，2004.DONG Jianhua.Modal analysis and tension measurement through and half through arch bridges［D］.Zhengzhou:Zhengzhou University，2004.

［3］罗勋.频率法测定斜拉索索力若干问题的研究［D］.成都:西南交通大学，2006.LUO Xun.Study of some issues of cable tension measurement by frequency method［D］.Chengdu:Southwest Jiao-tong University，2006.

［4］徐霞飞，任伟新.边界条件对吊索索力估算的影响［J］.铁道科学与工程学报，2008，5(6):26－31.XU Xiafei，Ren Weixin.Effect of boundary conditions on the estimation of suspender tension［J］.Journal of Railway Science and Engineering，2008，5(6):26 －31.

［5］何伟，陈淮，王博，等.复杂边界条件下基于频率法的吊杆张力测定研究［J］.土木工程学报，2012，45(3):93－98.HE Wei，CHEN Huai，WANG Bo，et al.Study of suspender tension measurement based on frequency method with complex boundary conditions［J］.China Civil Engineering Journal，2012，45(3):93 －98.

［6］王博妮.关于特定情况下柔性索索力－频率关系的研究［D］.成都:西南交通大学，2012.WANG Boni.Study on the tension －frequency relationship of flexible cable in particular situation［D］.Chengdu:Southwest Jiaotong University，2012.

［7］祖祥胜，刘征宇，柏国清.钢绞线拉索与钢丝拉索体系的比较［J］.安徽建筑，2010，17(3):26－28.ZU Xiangsheng，LIU Zhengyu，BAI Guoqing.Comparison of the steel stranded wire cable system and the steel wire cable system［J］.Anhui Architecture，2010，17(3):26－28.

［8］CUI Xin，JIANG Yong，FU Liwen，et al.The research on cable force measurement based on degenerated element with frequency method［J］.Applied Mechanics and Materials，2013(405－408):1709－1715.

［9］Geier R，De Roeck G，Flesch R.Accurate cable force determination using ambient vibration measurements［J］.Structure and Infrastructure Engineering，2006，2(1):43－52.

［10］JTG/T D65－01－2007，公路斜拉桥设计细则［S］.JTG/T D65－01－2007，Guidelines for design of highway cable－stay bridge［S］.

［11］陈林.平行钢绞线斜拉索施工技术［J］.公路交通技术，2008(5):66－69.CHEN Lin.Construction technique of parallel steel stranded wire stay cable［J］.Technology of Highway and Transport，2008(5):66 －69.

［12］姜玉刚.平行钢铰线斜拉桥的施工控制研究［D］.西安:长安大学，2005.JIANG Yugang.Study on construction control of parallel strand cable－ stayed bridge［D］.Xi’an:Chang’an U-niversity，2005.

［13］徐宏，黄平明.平行钢丝拉索Daniel效应分析［J］.铁道科学与工程学报，2008，5(2):38－41.XU Hong，HUANG Pingming.Analysis of daniel effect for parallel wire cable［J］.Journal of Railway Science and Engineering，2008，5(2):38 －41.