预应力锚索框架梁加固滑坡的稳定性数值分析①

戴自航，石金华，卢才金

(1.福州大学岩土工程研究所，福建 福州 350108;2.卧龙岗大学土木、采矿与环境工程学院，澳大利亚新南威尔士洲 2522;3.福州市建筑设计院，福建 福州 350001;4.福建省交通规划设计院，福建 福州 350004)

上世纪80年代以前，滑坡治理常用的方式主要有两种类型:一种是滑坡后方减重、前方压重并在滑坡后部、坡面或坡体内部设置立体排水体系;第二种则主要采用重力式挡墙、抗滑桩等以荷载——结构模式为基本特征的被动加固措施［1－3］。20世纪80年代以来，随着岩土锚固技术的发展，预应力锚索(包括锚杆，以下皆同)框架梁(如图1所示)作为一种相对新型的抗滑支挡结构在滑坡治理和边坡加固工程中得到了广泛应用［4］，这种支挡结构通过预应力锚索调动滑动面以外稳定地层的自稳能力，并通过框架梁将锚头施加在其上的预应力传递到宽广的岩土体表面，是一种主动加固方式。相对于重力式挡墙、普通抗滑桩等被动支挡结构，其具有结构轻巧美观、圬工少、造价低、施工安全、可提高滑动面抗剪强度等许多优点，具有显著的经济效益。故近些年来，该结构在全国各地的滑坡治理和边坡加固工程中随处可见。许多学者采用不同的研究方法，如理论研究、试验研究和数值模拟对边(滑)坡预应力锚索框架梁的内力分布进行了有益的探讨，而对加固前后滑坡的稳定性分析则相对笼统或仅作简要阐述。然而，滑坡治理前后的稳定性分析是滑坡治理设计的关键环节之一，是滑坡治理方案确定，进行支挡结构设计的依据。目前边(滑)坡稳定性分析方法众多，总体上包括极限平衡法、极限分析法、滑移线法和有限元等数值分析法。前几种方法可认为是基于刚塑性或理想弹塑性假设基础上的解析法，而有限元等数值分析法引入能反映应力－应变关系的非线性弹塑性本构模型，可以描述坡体内受力状态，并且满足变形协调关系和各项静力平衡条件，在边坡稳定分析中是一种理论上更加严密的方法［5-8］。另外，有限元法不受边坡模型形状限制，可模拟不同工况和施工顺序对边(滑)坡稳定性的影响，并可建立土体与支挡结构物的接触关系来模拟两者间的共同和相互作用效应。显然，预应力锚索框架梁治理滑坡的问题是一典型的复杂的三维问题，传统的解析方法难以合理的对采用该结构治理的滑坡进行稳定性分析，而有限元等数值分析法可能是解决该问题的较好途径，但目前已进行的数值分析大多仍将该问题简化成平面问题，很少按三维问题来分析，少有的采用三维数值模拟分析预应力锚索框架梁治理滑坡时，也均对整体受力条件作了一些偏于实际的简化［9-11］，没有充分考虑框架梁、锚索、灌浆体和坡体间的相互接触关系，研究重点主要集中在锚固体的剪应力或是框架梁下的岩土体附加应力，鲜有关于预应力锚索框架梁治理滑坡的稳定性分析的研究报道。本文以采用框架梁加固的某存在古滑坡的路堑边坡为例，充分考虑框架梁、锚索、灌浆体和岩土体间的相互作用，建立符合实际的真三维有限元模型，采用强度折减有限元法分析预应力锚索框架梁加固该滑坡后的稳定性。

图1 某高速公路路堑边坡预应力锚索框架梁加固工程Fig.1 A road cutting slope stabilized by framed beams with prestressed cables

1 工程实例概况

该工程为福建省漳(漳州)龙(龙岩)高速公路K64+690～790和溪段路堑边坡工程。边坡场地地貌上属于低山－丘陵区，原始地形坡面起伏较大，陡缓相间，边坡两侧凸出，两边凹进，中部有沼泽化现象，自然坡度为20°～40°，平均坡度35°，主要岩性为第四系全新统坡积层、残积层，下伏白垩系花岗闪长岩以及坡脚及路面分布的边坡开挖堆积土等，为花岗岩风化壳类土质边坡。为满足该高速公路用地需求，原设计按相关规范对该边坡实施放坡开挖，分3级放坡，第1级坡率1∶0.75，坡高5 m;第 2 级坡率 1∶1.2，坡高 8 m;第 3级坡率1∶2.0，坡高8.75 m。但在边坡局部放坡开挖时发现坡脚坡积土和残积土交界面处存在明显的摩擦痕迹，且边坡变形呈显著增长趋势，经判断确定该边坡为曾经的古滑坡滑动后的遗留体。必须认真对在该古滑坡上进行路堑边坡开挖的稳定性进行分析，并根据分析结果采取相应的措施。

2 古滑坡放坡开挖下的稳定性分析

当没有采取任何支挡结构时，通常情况下，按平面应变问题进行边(滑)坡的稳定分析不但可减少计算工作量，而且也能获得可靠的分析结果，在普通计算机上就可完成。因此，下文对放坡开挖该古滑坡的稳定性按平面应变有限元法进行分析，采用国际著名的非线性有限元程序ABAQUS建立其二维模型，如图2所示，模型前缘以公路中心线为界，后缘以坡顶前缘向后延伸6 m为界，下边界取至路面以下12 m。根据场地地层分布及坡脚滑动面的揭露情况，分析中认为古滑坡的滑动面为坡积土与残积土的交界面，且仍是其复活的潜在滑动面，以滑动带表征古滑坡特性，取滑带土厚度0.6 m。岩土体按莫尔－库仑理想弹塑性材料模拟，根据工程勘察报告，边坡各岩土层参数见表1(其中滑带土指标为坡积土重复剪切试验的残余强度指标)。稳定分析采用有限元强度折减法。

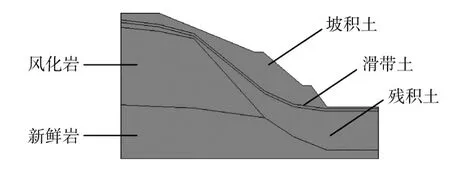
图2 古滑坡放坡开挖二维有限元模型Fig.2 2D FEM model of the excavation ancient landslide

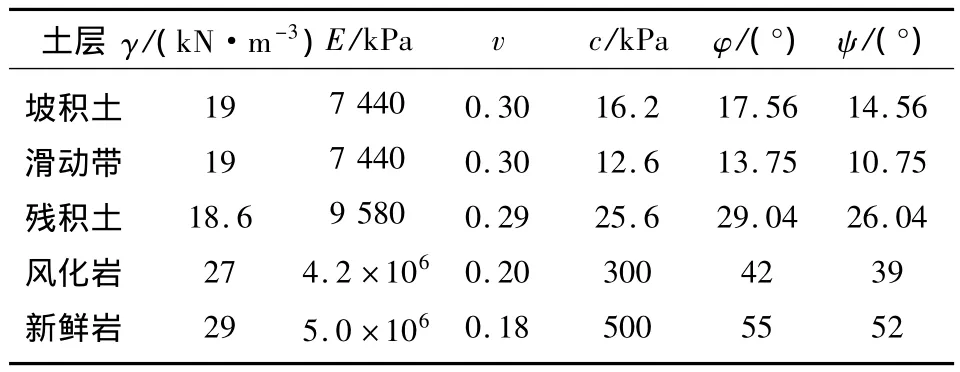
表1 岩土体材料参数Table 1 Property parameters of soil and rock

目前采用有限元强度折减法进行边坡稳定分析时，关于失稳的判据大致分为3类［5－8］:

(1)以数值计算不收敛为标准;

(2)以塑性区(等效塑性应变)临界贯通为标准;

(3)以土体中出现位移突变(位移拐点)且无限发展为标准。

这3类标准目前并没有达成一致的意见，而不同的失稳判据有时会得到相差悬殊的结果。笔者曾做的大量计算表明［12］，上述第1种判据与后2种的差别常较大，以数值计算不收敛为标准常可能得出偏于不安全的结果。后2种判据所得结果通常较为一致，故笔者认为，将该两者结合起来作为边(滑)坡失稳的判据是较为可靠的，且第3种判据是国际上较常采用的方法［13］。

图3给出了放破开挖下该古滑坡坡脚处水平位移与强度折减系数的关系曲线。曲线曲率最大拐点对应的强度折减系数为0.869，从该点开始水平位移开始快速增长。实际上，随着强度折减系数的增大，边坡内等效塑性应变(与广义塑性剪应变对应)的发展如图4和图5所示，可见，边坡滑动带上部土体最先出现塑性屈服，随着Fs的增大，边坡滑动带的塑性区逐渐向坡脚延伸，当Fs=0.869时，塑性剪应变区已临界贯通，据此可认为此时该古滑坡的安全系数Fs=0.869。显然，若按原设计的3级放坡开挖而不作任何加固处理，必将引起该古滑坡复活，再次产生滑动，这与之前局部放坡开挖时边坡变形迹象相吻合。

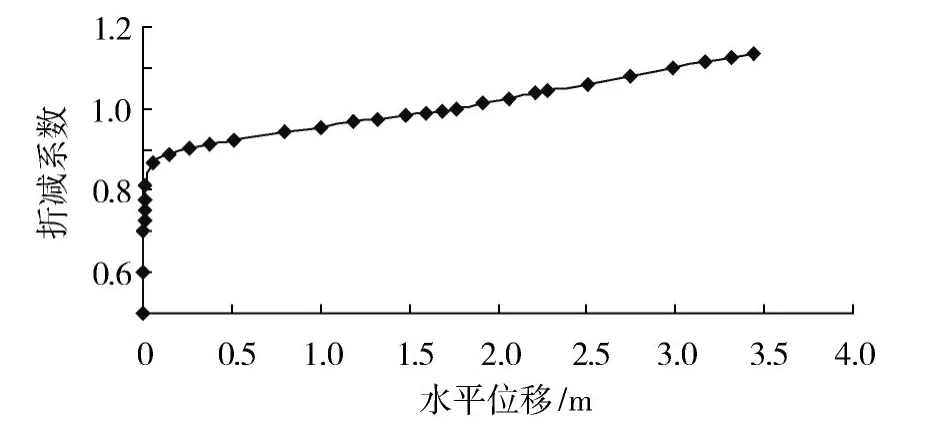
图3 边坡坡脚水平位移与折减系数关系曲线Fig.3 Curve of slope toe horizontal displacements versus reduction coefficients

图4 Fr=0.775时古滑坡土体等效塑性应变等值云Fig.4 Equivalent plastic strain nephogram in the ancient landslide as Fr=0.775

图5 Fr=0.869时古滑坡土体等效塑性应变等值云Fig.5 Equivalent plastic strain nephogram in the ancient landslide as Fr=0.869

3 预应力锚索框架梁加固后稳定性分析

二维稳定性分析结果表明:若按图1所示放坡开挖必须对该古滑坡进行加固处理，设计采用预应力锚索框架梁进行加固。并对预应力锚索框架梁加固后古滑坡体的稳定性进行三维有限元分析，其分析是在建立于福州大学的福建省超机计算中心的平台上完成。图6所示为采用1排框架梁加固的真三维有限元模型，框架梁与坡面采用库仑摩擦接触进行模拟，锚索和框架梁按绑定约束模拟，灌浆体与土体的接触采用黏着摩擦(ABAQUS中实现)进行模拟。边坡底部位移边界约束三个坐标方向位移，边坡前后侧约束x向位移，左右侧约束y向位移。

本文分别探讨了采用1排和2排框架梁加固该古滑坡的稳定安全系数，所述框架梁形如图7所示，由2根竖肋和2根横梁组成的“井”字形，顺坡方向分布1#和2#竖肋，A横梁和B横梁则垂直坡向分布，一般相邻2排框架梁横梁端部间距仅10 cm，故从远处看上去是紧密相联的，如图1。本文分析中，不考虑锚索与灌浆体之间的摩擦，而采用嵌入约束，即锚索与灌浆体之间无相对滑移，锚索自由段与周围土体间无相互作用或光滑无摩擦。锚索、框架梁和灌浆体关系如图8所示。为提供足够的锚固力，锚索采用φ15.24低松弛预应力高强钢绞线，孔径150 mm，每孔7根锚索，锚索全长20 m，锚固段劈裂灌浆10 m。每根锚索采用600 kN预拉力进行张拉锁定，有限元数值模拟中通过“降温法”来对锚索施加预拉力。

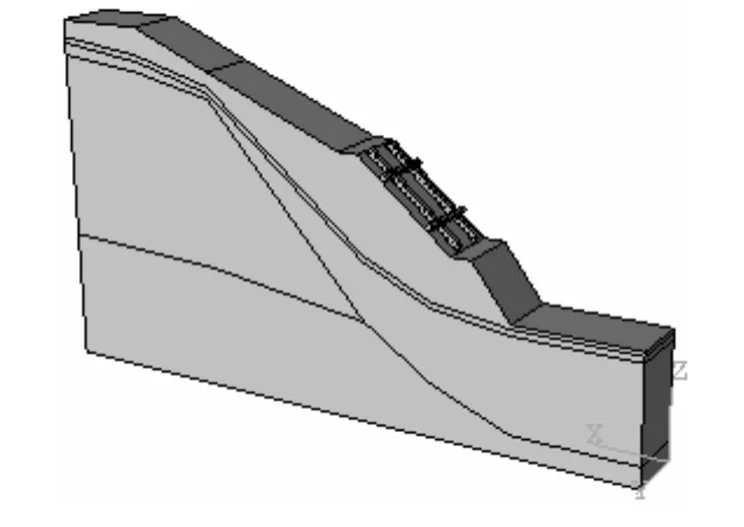
图6 1排预应力锚索框架梁加固古滑坡整体模型Fig.6 Whole model stabilized by a row of framed beams with prestressed cables

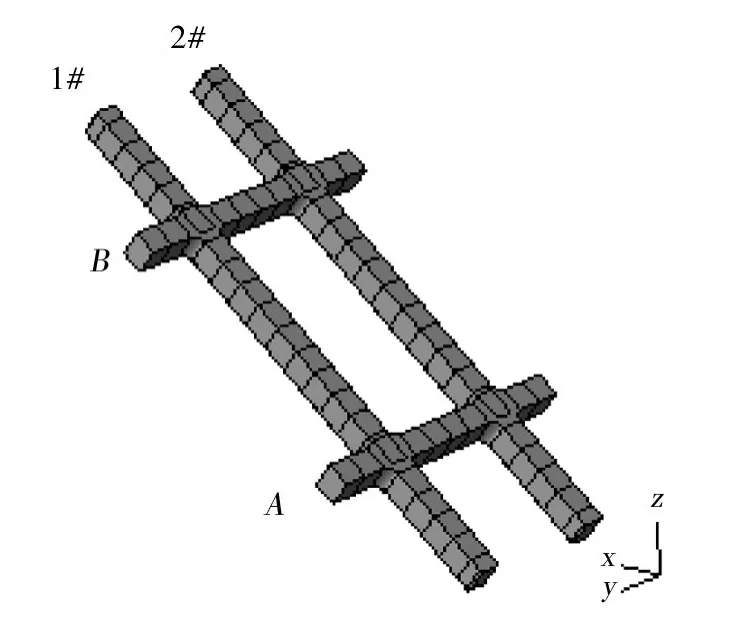
图7 框架梁结构放大Fig.7 Magnified framed

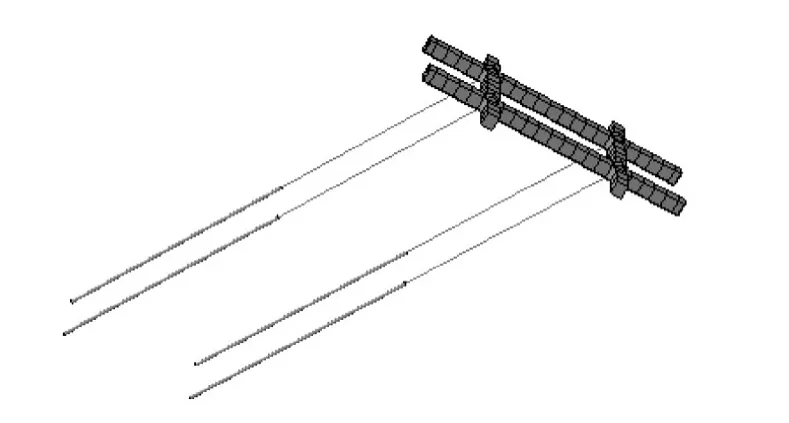
图8 锚索、框架梁和灌浆体模型Fig.8 Model of anchor cables，framed beams and grouting bodies

由于实际工程中灌浆体与岩土间的接触相互作用有黏着和库仑摩擦，即灌浆体与岩土之间发生相对剪切滑移时，也遵循莫尔 －库仑定理。但ABAQUS程序中并无莫尔－库仑黏着摩擦接触特性的定义，为此，笔者提出下式

式中:p为接触面上的接触压力;μ'=μ+c/p。

若岩土与灌浆体接触面的外摩擦系数μ=0.3，黏着力c=10 kPa，则μ'=0.3+10/p(通常μ'≤1)，其中p可在接触范围内取土的自重应力。本文根据我省类似工程的试验结果的反分析得到μ=0.45，c=30 kPa，在灌浆体与岩土体接触范围内，按μ'的表达式建立其随接触压力变化的数据表，这样无需开发莫尔 －库仑黏着摩擦特性用户子程序，用ABAQUS程序中经典库仑摩擦特性仍可较好地模拟具有莫尔－库仑黏着摩擦特性的接触问题。

锚索端部与锚斜托采用分布耦合约束，将预应力均匀施加在锚斜托上。三维模型网格划分采用C3D10M(修正的10节点四面体单元)，图5所示模型的网格透视图如图9所示。

图9 模型的三维透视网格Fig.9 Perspective meshes of 3D model

框架梁，锚斜托和锚索等几何及物理力学参数参照钢结构设计规范和混凝土结构规范如表2所示。

表2 锚索框架梁结构物材料参数Table 2 Property parameters of framed beam with cables

图10给出了1排预应力锚索框架梁加固古滑坡后，坡脚处水平位移与折减系数的关系曲线。从图中可以看出，当折减系数为1.138时，即对应曲线曲率最大拐点的折减系数，坡脚已经开始出现位移急剧增长趋势，据此可确定经1排预应力锚索框架梁加固后该边坡的安全系数Fs=1.138。

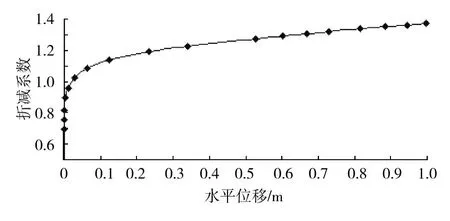
图10 1排框架梁加固时坡脚水平位移与折减系数关系曲线Fig.10 Curve of slope toe horizontal displacements versus reduction coefficients while stabilized by a row of framed beams

与平面应变模型对比，当Fr=1.082时，古滑坡内的滑动带上部最早出现塑性区，如图11所示，且塑性区随着Fr的增长而向下延伸，当Fr=1.138时，塑性区临界贯通，如图12所示。同时框架梁与坡面接触处附近土体也出现了塑性区，这与锚索预拉力作用有关，锚索预张拉使框架梁压入坡面土体，使附近土体产生剪切屈服或破坏，这与实际施工情况相吻合。

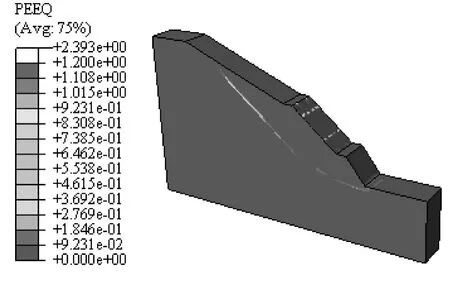
图11 Fr=1.0821排框架梁加固古滑坡时等效塑性应变等值云Fig.11 Equivalent plastic strain nephogram in the ancient landslide stabilized with a row of framed beams as Fr=1.082

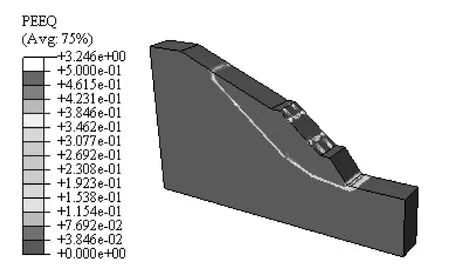
图12 Fr=1.1381排框架梁加固古滑坡时等效塑性应变等值云Fig.12 Equivalent plastic strain nephogram in the ancient landslide stabilized with a row of framed beams as Fr=1.138

显然，在第2级坡面施加1排预应力锚索框架梁后，明显提高了古滑坡的抗滑能力，稳定安全系数从放坡开挖不作加固处理的0.865提高到了1.138，但此安全系数仍无法满足工程设计需要。另外，从图13也可以看出，当古滑坡处于临界稳定状态时，古滑坡在第1级坡面的水平位移较大，坡脚隆起量也较大，第3级坡面水平位移也较大，而第2级坡面水平位移则相对较小，说明仅在古滑坡第2级坡面处采用预应力锚索框架梁加固的作用主要是通过改变滑体的应力提高了第2级坡面对应滑带土的抗剪强度。为进一步提高整体稳定安全系数，在第3级坡面设置第2排锚索框架梁，如图14所示。

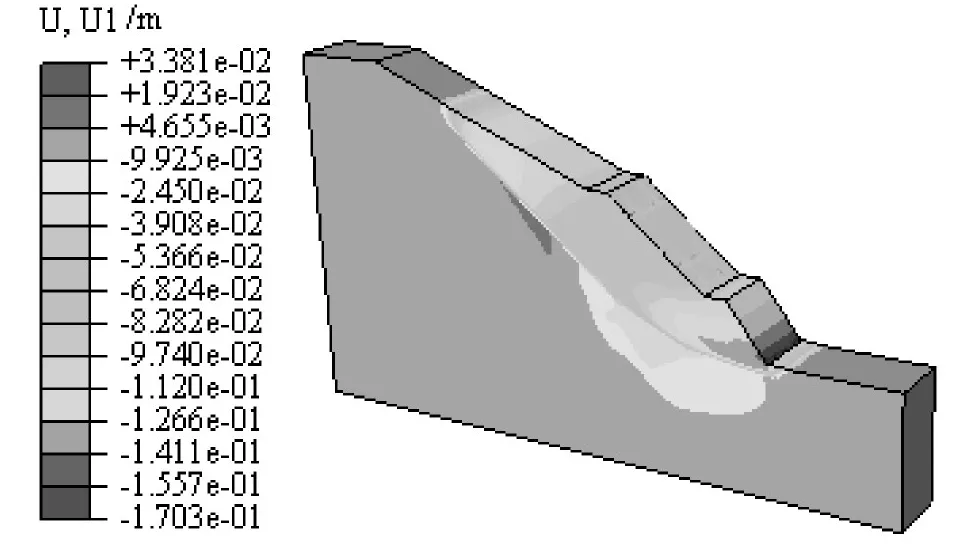
图13 1排框架梁加固时古滑坡临界稳定状态水平位移等值云Fig.13 Horizontal displacement nephogram in critical state with a row of framed beams to reinforce the ancient landslide

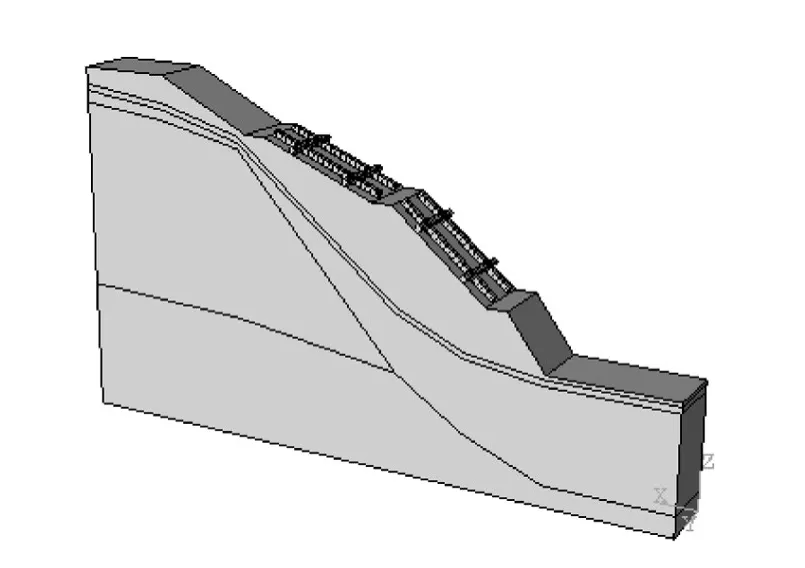
图14 2排预应力锚索框架梁加固滑坡整体模型Fig.14 Whole model stabilized by two rows of framed beams with prestressed cables

图15为施加第2排预应力锚索框架梁后，古滑坡坡脚处水平位移与折减系数的关系曲线。从图中可以看出，当Fr=1.203，坡脚已经开始出现位移急剧增长趋势，同时塑性区临界贯通(见图16)，据此可确定经2排预应力锚索框架梁加固后该边坡的稳定安全系数Fs=1.203。

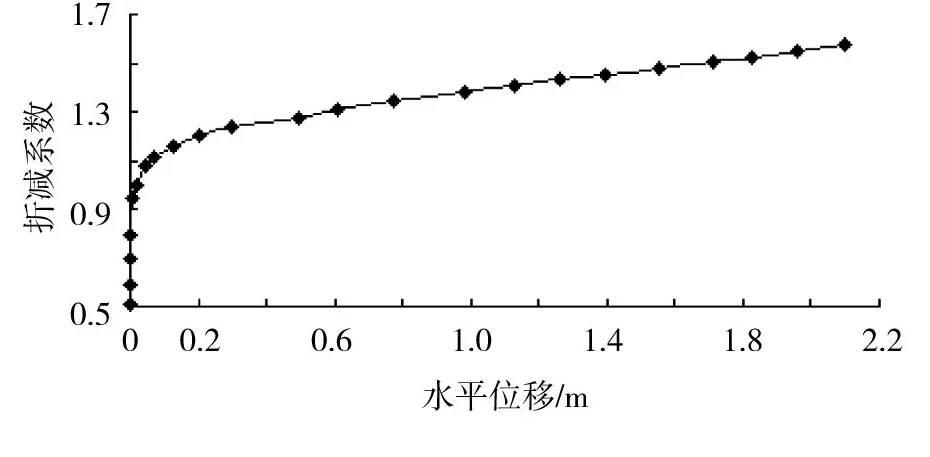
图15 2排框架梁加固时坡脚水平位移与折减系数关系曲线Fig.15 Curve of slope toe horizontal displacements versus reduction coefficients while stabilized by two rows framed beams

实际施工中，各级边坡开挖和支护顺序是自上而下进行的，先开挖第3级边坡，设置1排预应力锚索框架梁，由图17可以看到第3级边坡土体位移变化情况。由于第3级坡面处坡积土和残积土层较薄，风化岩较浅，在预应力作用下，浅层土体压缩变形呈漏斗状，由浅及深逐渐减小，边坡加固范围扩展到第2级坡面平台处，坡体内则达到残积土与风化岩交界面，有效利用稳定土层的抗滑力。

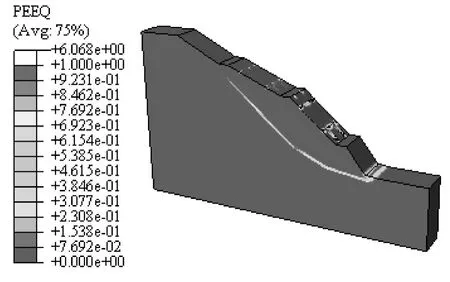
图16 Fr=1.2032排框架梁加固古滑坡时等效塑性应变等值云Fig.16 Equivalent plastic strain nephogram in the ancient landslide stabilized with two rows of framed beams as Fr=1.138

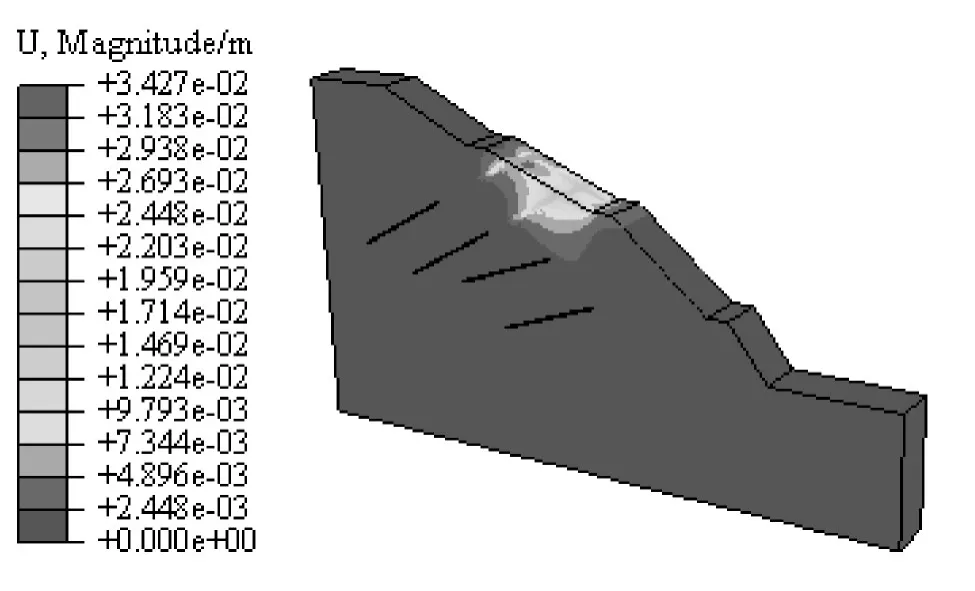
图17 第3级边坡设置框架梁时古滑坡位移等值云Fig.17 Displacement nephogram in the ancient landslide while framed beams is set on the third level of the ancient landslide

再开挖第2级边坡，设置另一排预应力锚索框架梁，此时在两排框架梁叠加作用下，第2级和第3级梁下土体向坡体内压缩，在边坡中上部土体压缩区连成一片，如图18所示，使边坡中上部岩土体处于三向受压状态，使滑带土的抗剪强度得到显著提高。表3为1排和2排预应力锚索框架梁加固作用下，边坡的稳定安全系数变化情况。从中可以看出，在第2级坡面施加1排预应力锚索框架梁时，稳定安全系数较放坡开挖提高幅度为31.6%。采用2排预应力锚索框架梁加固后，使古滑坡体开挖边坡的稳定安全系数满足了设计要求的1.2以上。但可以看到在第3级坡面增设预应力锚索框架梁对边坡稳定安全系数的提升效果不是很显著，较仅在第2级边坡上设置1排框架梁加固时，仅提高了7.5%。这主要是因为此时边坡的破坏主要是由于第1级坡面仅采用了片石护坡，在强度折减到1.203时，坡脚发生剪切贯通，导致边坡开始失稳。实际工程中有的在第1级边坡坡脚设置重力式挡墙作为辅助支挡结构，不仅可防止雨水冲刷，而且可进一步提高边坡的稳定安全系数。

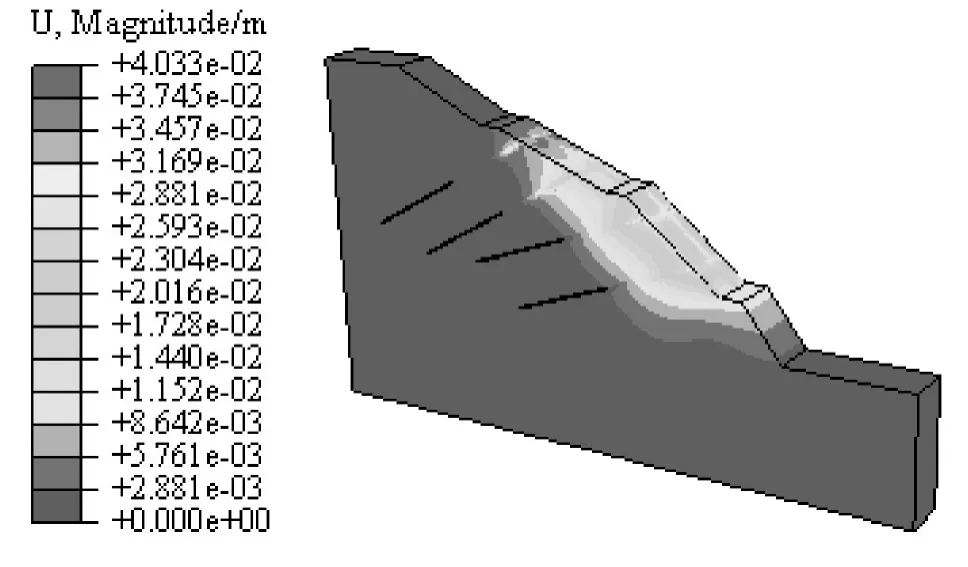
图18 2排框架梁作用下古滑坡位移等值云Fig.18 Displacements nephogram in the ancient landslide while two rows of framed beams are set

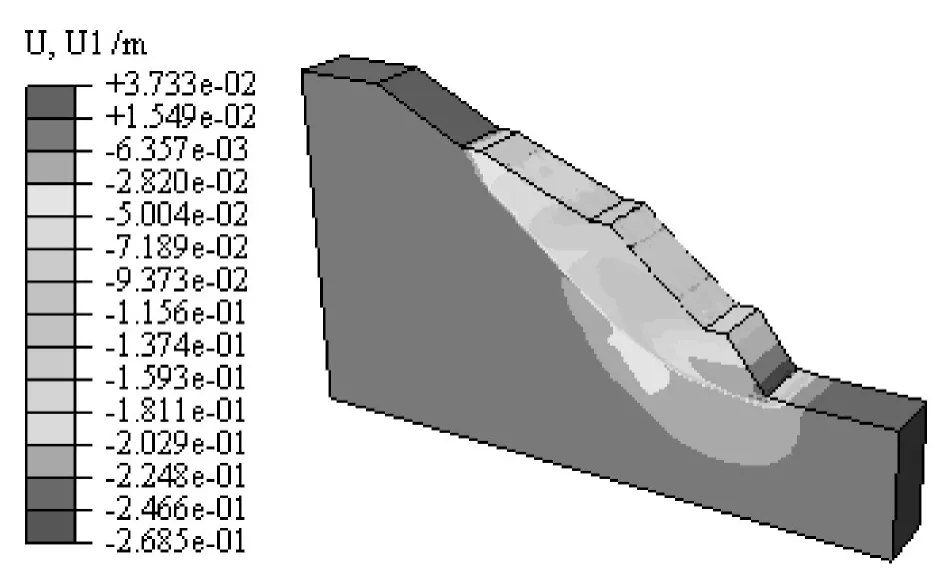
图19 2排框架梁加固下临界稳定状态水平位移等值云Fig.19 Horizontal displacement nephogram in critical state while reinforced with two rows of framed beams

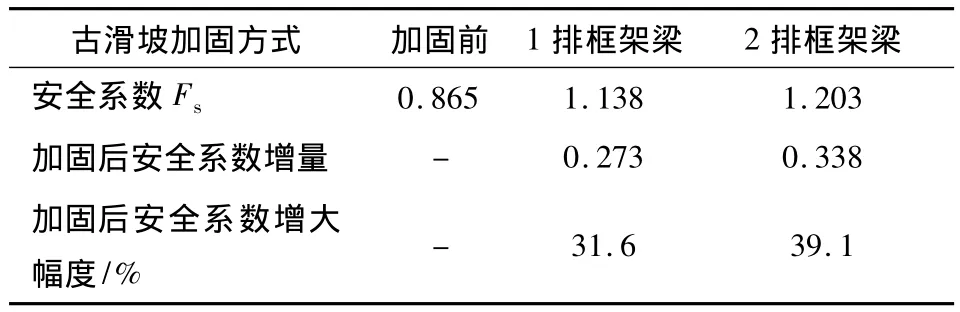
表3 加固前后古滑坡的稳定安全系数比较Table 3 Comparison of safety factors while the ancient landslide is reinforced or not

4 结论

(1)采用平面应变有限元模型按强度折减法进行古滑坡加固前的稳定分析，不仅可减少计算工作量，而且能获得可靠的分析结果。可作为抗滑支挡结构选型和设计的依据。

(2)有限元强度折减法进行边(滑)坡稳定分析时，以特征点位移－折减系数曲线上曲率最大拐点与塑性剪应变区临界贯通相结合的失稳判据是适合的。

(3)预应力锚索框架梁治理滑坡的问题是典型的三维问题，采用平面应变方法进行加固后的稳定分析难以获得可靠的分析结果，采用本文介绍的符合实际的三维实体有限元模型且将灌浆体和岩土体的接触作用按莫尔－库仑黏着摩擦考虑，其结果将更可靠。

(4)考虑锚索、框架梁和灌浆体三者间的相互作用，模拟获得了预应力锚索框架梁的作用机理。分析显示，由于群锚效应引起浅层土体压缩，并通过锚索将预应力传递给了灌浆体，由其分散到稳定土层中，表明预应力锚索框架梁是一种主动加固体系，能有效改善边坡的应力状态。

(5)分析结果表明:预应力锚索框架梁设置在边坡的中下部对提高边坡的稳定性作用显著，而设置在边坡上部对边坡稳定性贡献较小，主要原因在于边坡最先失衡的部位可能将转化为坡脚附近土体的失稳，故在坡脚辅以抗滑挡墙具有积极意义。

［1］陈启正.金鸡岩集中工业广场抗滑桩的施工［C］//滑坡文集(第六集).北京:中国铁道出版社，1988.CHENG Qizheng.The construction of anti－ slide pile in Jinjiyan concentrated industrial square［C］//Landslide Corpus(the sixth set).Beijing:Chinese Railway Press，1988.

［2］铁道部科学研究院西北研究所.预应力锚索抗滑桩试验研究［R］.兰州:铁道部科学研究院西北研究所，1989.Northwest Institute of Mor Scientific Research Institute.Test research of anti－ pile with prestressed cables［R］.Lanzhou:Northest Institute of MOR Scientific Research Institute，1989.

［3］王化卿.预应力锚索抗滑桩设计与施工［C］//滑坡文集(第七集)［M］.北京:中国铁道出版社，1990.WANG Huaqing.The design and construction of antislide pile with prestressed cables［C］//Landslide Corpus(the seventh set).Beijing:Chinese Railway Press，1990.

［4］程良奎，李象范.岩土锚固·土钉·喷射混凝土——原理、设计与应用［M］.北京:中国建筑工业出版社，2008.CHENG Liangkui，LI Xiangfan.Rock－soil anchoring·soil nail·jet concrete—principle，design and application［M］.Beijing:Chinese Construction Industry Press，2008.

［5］郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用［J］.岩石力学与工程学报，2004，23(19):3381 －3388.ZHENG Yingren，ZHAO Shangyi.Application of strength reduction FEM in soil and rock slope［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(19):3381－3388.

［6］栾茂田，武亚军，年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用［J］.防灾减灾工程学报，2003，23(3):1 －8.LUAN Maotian，WU Yajun，NIAN Tingkai.A critical for evaluating slope stability based on development of plastic zone by shear strength reduction FEM［J］.Journal of Seismology，2003，22(3):1－8.

［7］连镇营，韩国城，孔宪京.强度折减有限元法研究开挖边坡的稳定性［J］.岩土工程学报，2001，23(4):407－411.LIAN Zhenying，HAN Guocheng，KONG Xianjing.Stability analysis of excavation by strength reduction FEM［J］.Chinese Journal of Geotechnical Engineering，2001，23(4):407－411.

［8］赵尚毅，郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数［J］.岩土工程学报，2002，24(3):343－346.ZHAO Shangyi，ZHENG Yingren，SHI Weimin，et al.Analysis on safety factor of slope by strength reduction FEM［J］.Chinese Journal of Geotechnical Engineering，2002，24(3):343－346.

［9］吴礼舟，黄润秋.锚杆框架梁加固膨胀土边坡的数值模拟及优化［J］.岩土力学，2006，27(4):605 －608.WU Lizhou，HUANG Runqiu.Numerical simulation and optimum design of anchor frame beam strengthening expansive soil slope［J］.Rock and Soil Mechanics，2006，27(4):605－608.

［10］丁秀美，黄润秋，臧亚君.预应力锚索框架作用下附加应力的FLAc3D模拟［J］.成都理工大学学报(自然科学版)，2003，30(4):339 －345.DING Xiumei，HUANG Runqiu，ZANG Yajun.Three dimension simulation with FLAC3D on subsidary stress induced by frame beam with prestress cable［J］.Journal of Chengdu University of Technology(Science＆Technology Edition)，2003，30(4):339－345.

［11］张华，陆阳，程强.岩质边坡锚杆(索)框架梁加固的数值模拟［J］.公路交通科技，2008，25(1):21 －26.ZHANG Hua，LU Yang，CHENG Qiang.Numerical simulation of reinforcement for rock slope with rockbolt(anchor cable)frame beam［J］.Journal of Highway and Tramsprtation Research and Development，2008，25(1):21－26.

［12］戴自航，徐祥.边坡抗滑桩设计计算的三维有限元法［J］.岩石力学与工程学报，2012，31(12):2572 －2578.DAI Zihang，XU Xiang.3D Finite Element method for design computations of anti－ slide piles［J］.Chinese Journal of Rock Mechanics and Engineering，2012，31(12):2572－2578.

［13］Smith I M，Griffiths D V.Programming the finite element method［M］.3rd edition.John Wiley ＆ Sons，Inc，1998.