设置加强层的钢框架－核心筒结构的动力弹塑性时程分析①

蔡勇，罗应松，陆铁坚

(中南大学土木工程学院，湖南 长沙 410075)

钢框架－核心筒混合结构是广泛应用于超高层建筑中的一种结构形式，但是超高层建筑的高宽比一般较大，尤其是核心筒体的高宽比，常常会达到12，甚至更大，在水平荷载的作用下，结构的弯曲变形成分很大，靠刚度很小的钢框架来协同作用，效果十分有限。因此，常常会在筒体和钢框架之间设置刚臂结构，即水平加强层，来增加结构的整体抗弯能力，使结构在地震荷载或风荷载作用下产生的侧移量能满足规范的限值［1］。水平加强层能有效地控制结构在风荷载作用下的顶点侧移和层间位移角，但在地震荷载作用下布置水平加强层会引起结构刚度、内力的突变，容易形成薄弱层，使结构难以呈现延性屈服机制。目前，在地震作用下水平加强层对结构抗震性能影响的研究还不够深入，大多停留在弹性阶段成简单模型的模拟与计算，没有考虑到结构的非线性以及其他因素的影响。本文通过对设置加强层和未设置加强层4个不同结构分别在7度、8度和9度罕遇地震动作用下进行弹塑性动力时程分析，研究设置不同数目加强层时结构的抗震性能。

1 分析实例

本文所采用基本模型为34层钢框架－混凝土核心筒混合结构，结构平面尺寸为21 m×21 m，各层层高3.3 m，总高112.2 m，混凝土核心筒面积约占1.36%。其结构平面布置图如图1所示。未设置加强层和设置加强层结构的层布置三维透视图如图2所示，加强层布置位置［2］见表1，构件材料参数见表2所示。混凝土核心筒四面对称开洞，门洞口尺寸为2000 mm×2000 mm。

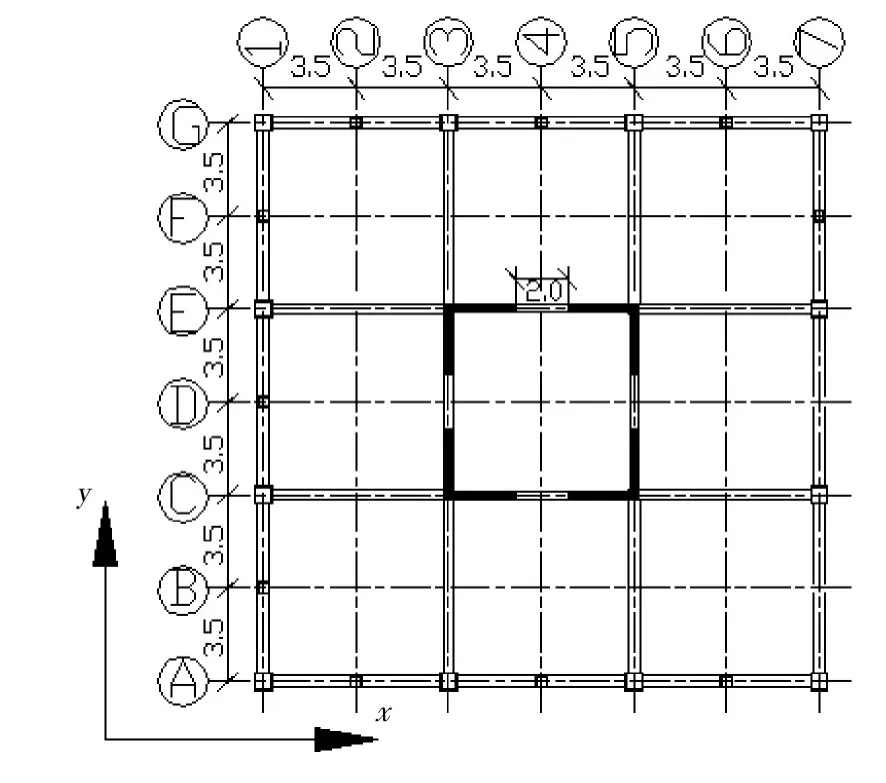
图1 结构平面图Fig.1 Structure plan

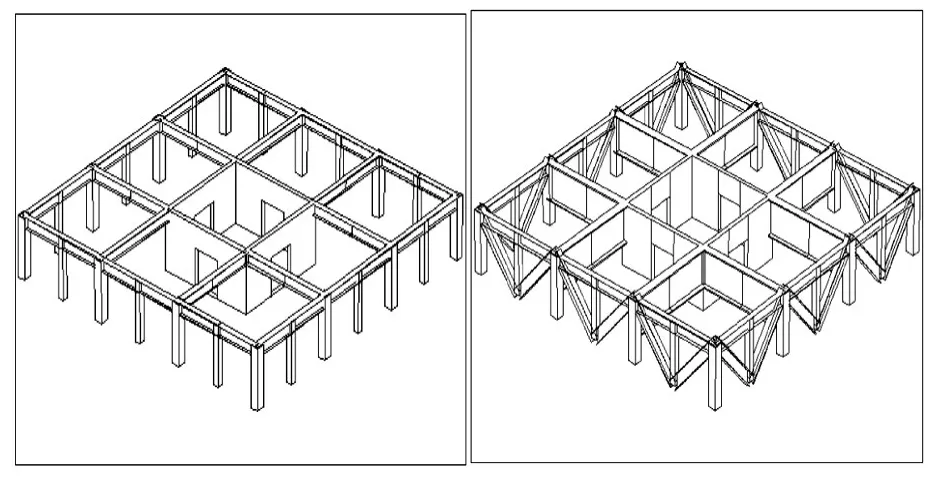
图2 未设置加强层与设置加强层的布置图Fig.2 Un－strengthening layer and strengthening layer layout

表1 加强层位置设置Table 1 Strengthen the position level set

2 模型建立

2.1 模型单元选择

2.1.1 弹塑性梁单元

弹塑性梁单元位移沿x轴采用3次Hermit插值。位移模式的变化主要体现在中轴线的位移，对于一般的杆件，中轴线的位移模式［3］:

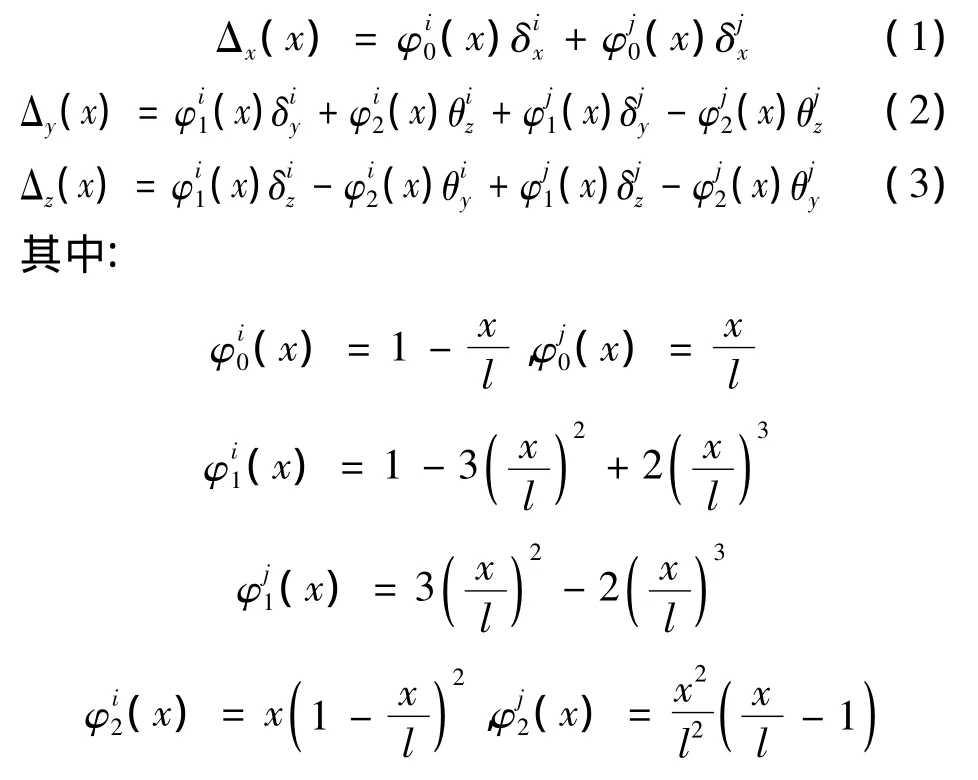
表2 构件材料参数Table 2 Component material properties

2.1.2 弹塑性墙单元

剪力墙主要在平面内提供刚度，平面外的刚度是次要的。所以，板部分只提供了一个近似的折减刚度矩阵，膜部分按照严格的应力一应变关系求刚度矩阵。剪力墙一般由混凝土和钢筋组成，其中钢筋是沿x，y正交不藕联。忽略钢筋的抗剪作用，取剪应力一项为“0”。钢筋的应力 －应变关系为［3］

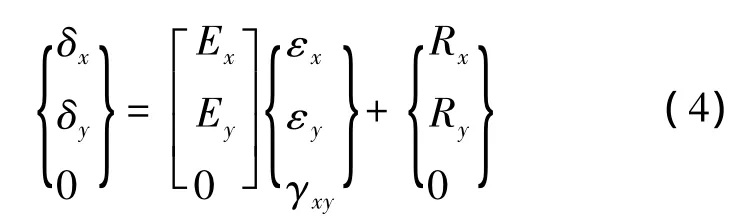
由于混凝土在双向应力下强度会发生变化［3］，直接影响式(4)的参数。本文选择Kupfer强度包络线。

2.2 结构材料力学模式与恢复力模型

采用弱化弹塑性拉断压碎有退化滞回模式［3］:该模式的滞回骨架通过能最等效从混凝土的Saenz曲线换算过来的。应力超过抗拉强度将一次性拉裂，下一次循环不能恢复;应力超过抗压强度则材料进入塑性，弹性模量小于0;滞回过程中发生退化。应变超过抗压极限应变，材料将彻底破坏，退出工作。

为了分析构件在地震作用下的动力响应，必须建立反复荷载作用下材料或截面性能准确的本构关系，即恢复力模型［4］。已有的恢复力模型可以大体分为2类［5］:折线型模型(PHM)和光滑曲线型模型(SHM)，其中折线型模型又主要分为双线型、三线型、四线型(带负刚度段)、退化二线型、退化三线型、指向原点型和滑移型7种。本文采用三线性模型。

3 结构动力特性分析

模态分析一般是用于确定结构的振动特性。本文用ANSYS采用分块兰索斯法提取模态［6－8］，4种结构模态分析结果如表3所示。

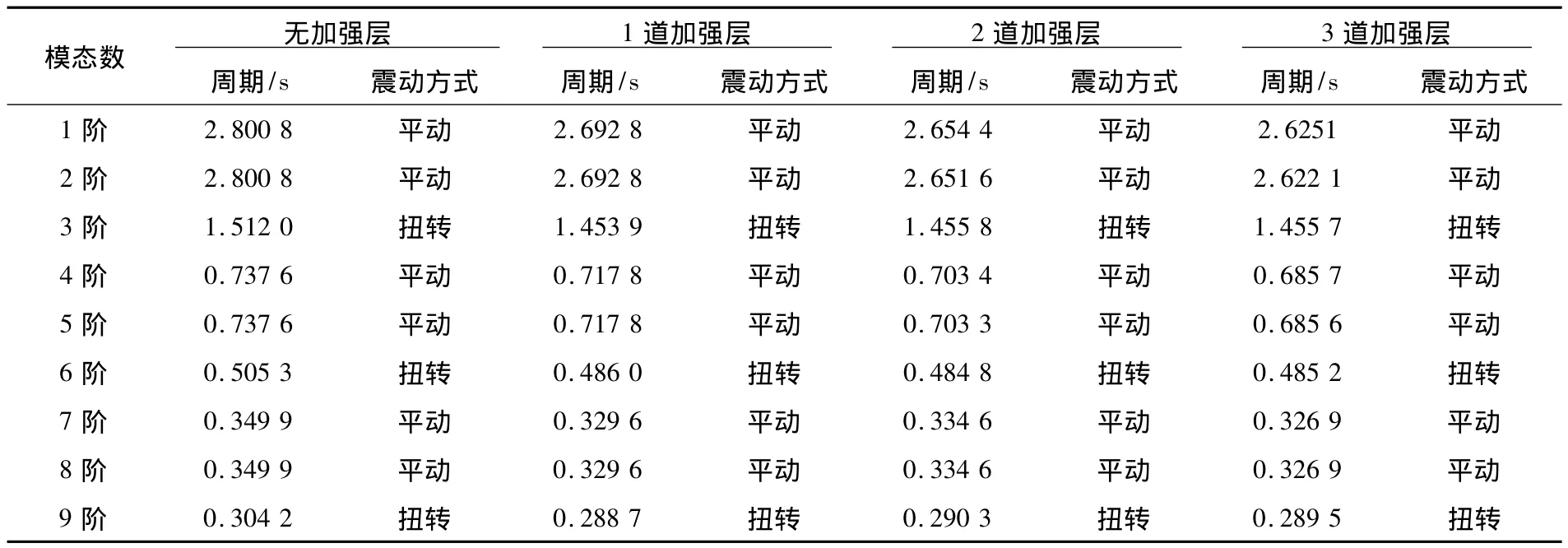
表3 不同结构形式的ANSYS模态分析结果Table 3 Model analysis result of Ansys for different structure

由表3可知:结构设置了加强层后，其中1阶、2阶、4阶和5阶平动自振周期会随加强层数的增多而降低;第3阶、6阶和9阶扭转自振周期变化不大;7阶和8阶平动自振周期基本没有变化。加强层数目的增加使得结构刚度增加，这对降低结构前6阶的自振周期有明显的作用。

4 弹塑性动力时程反应

4.1 分析方法

对不同峰值的地震作用下的结构位移反应进行比较，对选用的地震记录加速度峰值按规范规定的比例加以调整［9］，使峰值加速度相当于罕遇7度、8度和9度地震时的加速度峰值。地震动持时均选用30 s，地震动加载间隔为0.02 s。

EPDA计算时采用 Wilson－θ法［10－11］求解微分方程与Newton－Raphson法叠代求解非线性方程组，采用先进的PCG线性方程组解法使得计算结果精确并且容易收敛［12］。

4.2 动力弹塑性时程分析结果

4.2.1 4种结构动力弹塑性时程曲线

由图3、图4和图5可以看出:在7度、8度和9度罕遇地震作用下，设置加强层结构在各个时刻均比未设置加强层结构有更小的顶层侧移量;当设置多道加强层时，设置2道和3道加强层在各个时刻较设置1道加强层的顶层侧移量有明显的减少;但是设置3道与2道加强层对降低各个时刻顶层侧移量的效果几乎一样。

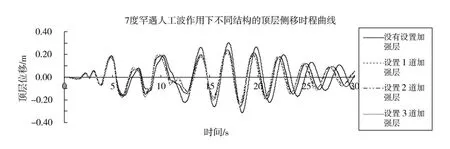
图3 7度罕遇人工波作用下不同结构主方向的顶层侧移时程曲线Fig.3 7degrees rare case of artificial waves of different top－level structure of the main directions of lateral versus time

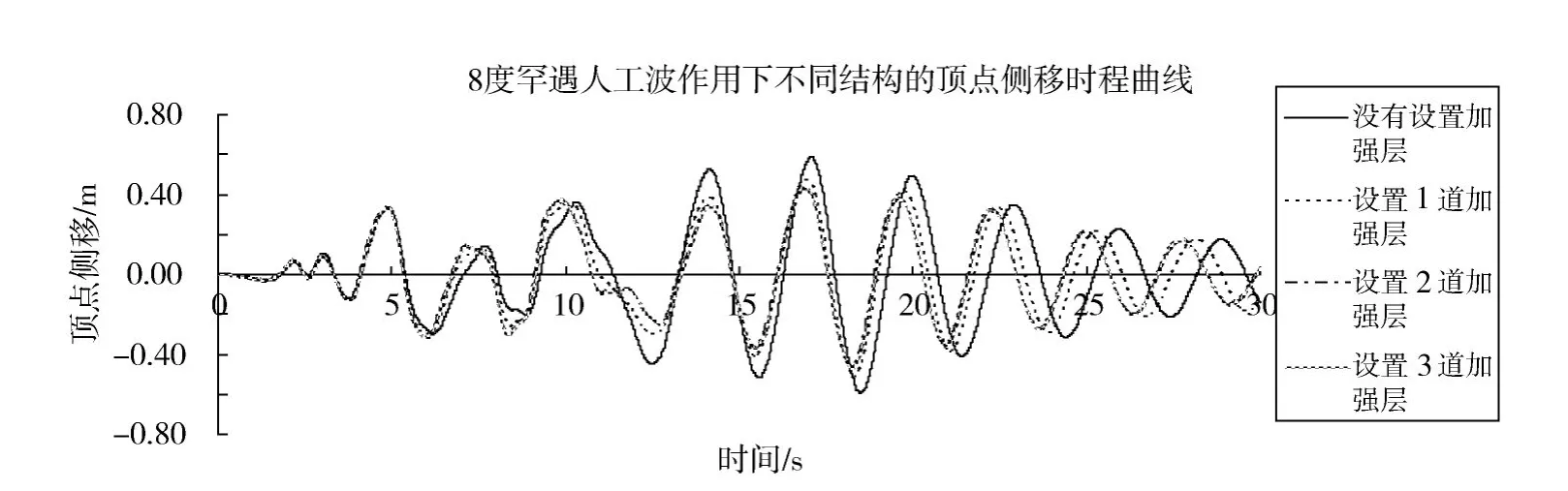
图4 8度罕遇人工波作用下不同结构的主方向顶层侧移时程曲线Fig.4 8degrees rare case of artificial waves of different top－level structure of the main directions of lateral versus time

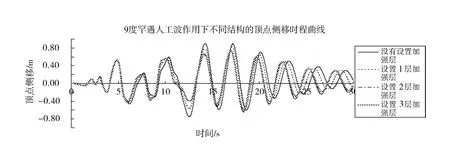
图5 9度罕遇人工波作用下不同结构的主方向顶层侧移时程曲线Fig.5 9degrees rare case of artificial waves of different top－level structure of the main directions of lateral versus time

4.2.2 4种结构动力弹塑性平均位移曲线、最大层间位移角曲线

由图6、图7、图8与表4可以看出:4种不同结构分别在7度、8度和9度罕遇地震作用下，设置了加强层的结构的平均层侧移与最大层间位移角明显小于没有设置加强层的结构;由图9可以看出，在7度、8度和9度罕遇地震作用下，设置2道加强层结构与设置3道加强层结构减少顶点侧移的效果相同，但是，设置2道加强层在减少层间位移角的效果上明显优于设置1道与设置3道加强层。

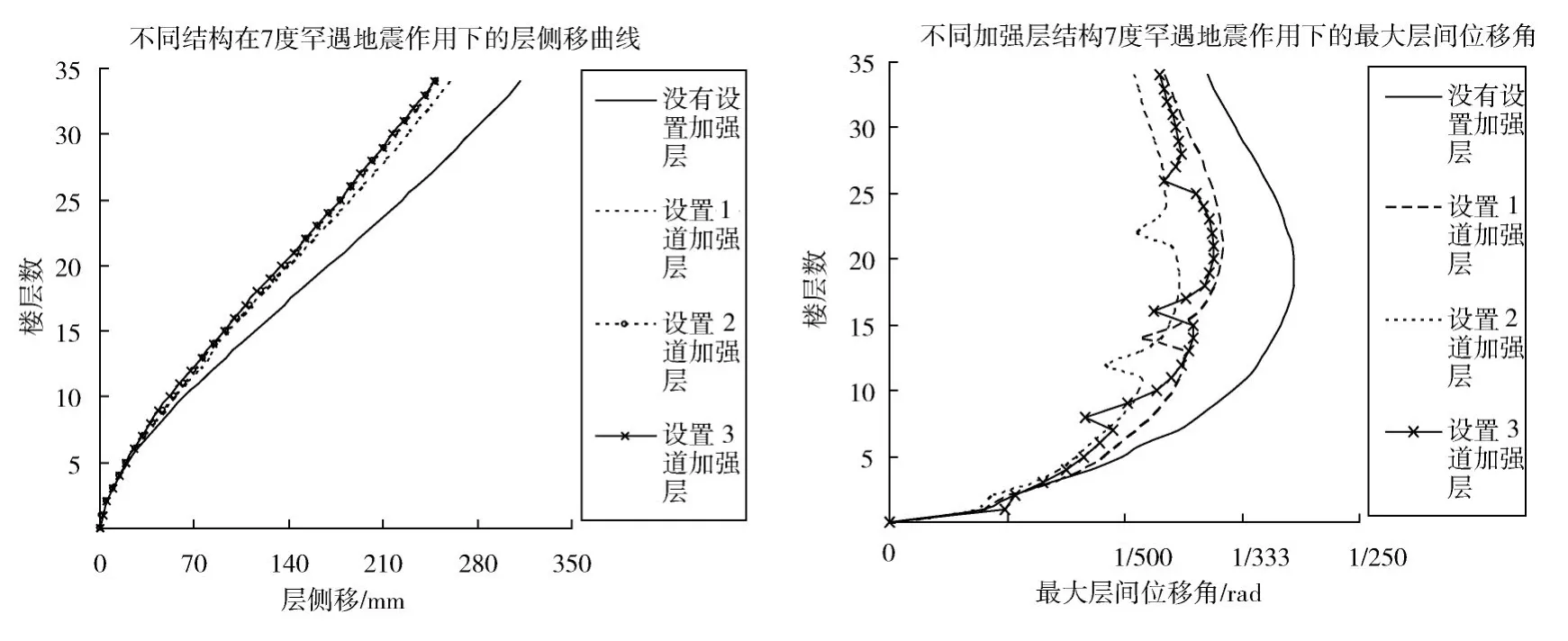
图6 7度罕遇地震波作用下四种结构平均层侧移与最大层间位移角图Fig.6 7degrees rare earthquake waves average of four layer structure of the lateral and the maximum story drift map

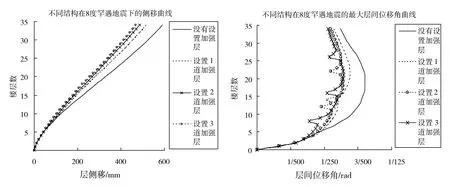
图7 8度罕遇地震波作用下四种结构平均层侧移与最大层间位移角图Fig.7 8degrees rare earthquake waves average of four layer structure of the lateral and the maximum story drift map

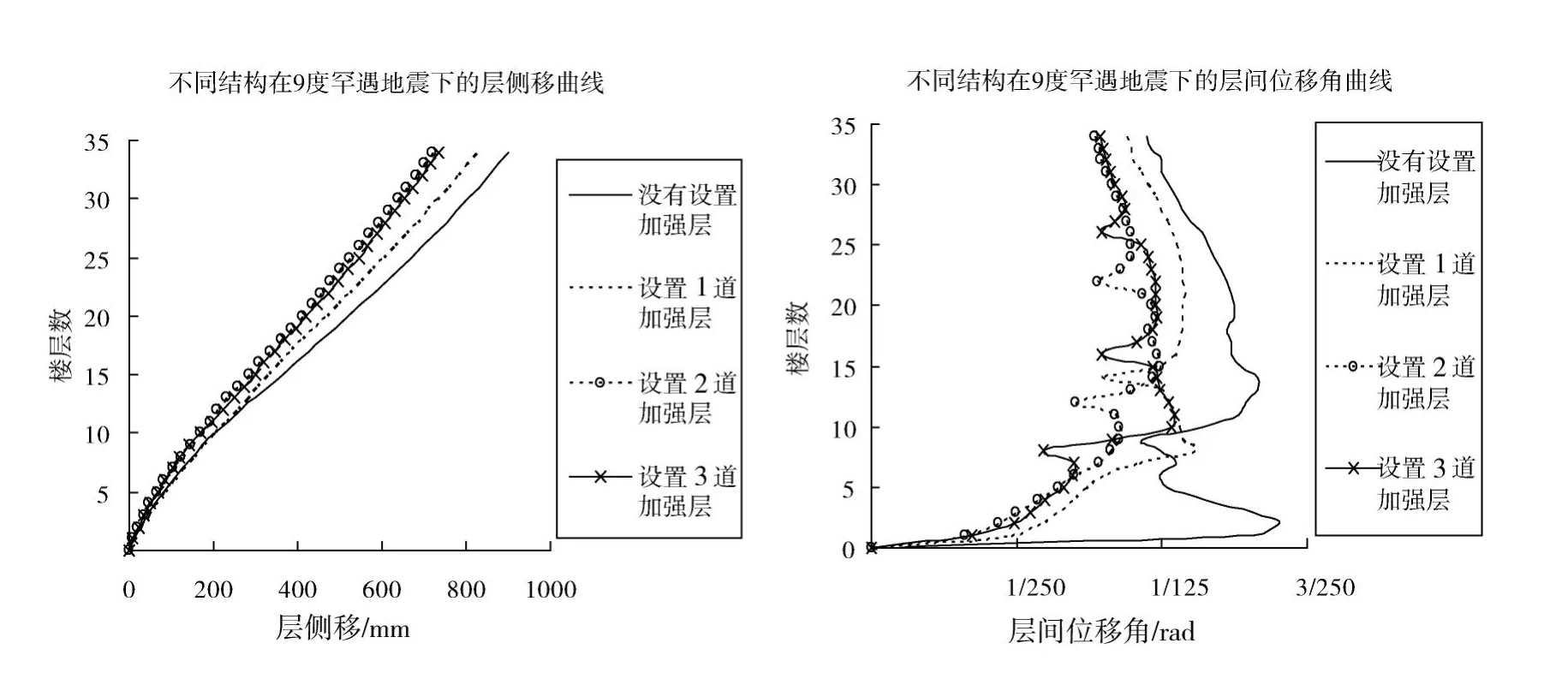
图8 9度罕遇地震波作用下4种结构平均层侧移与最大层间位移角图Fig.8 9degrees rare earthquake waves average of four layer structure of the lateral and the maximum story drift map

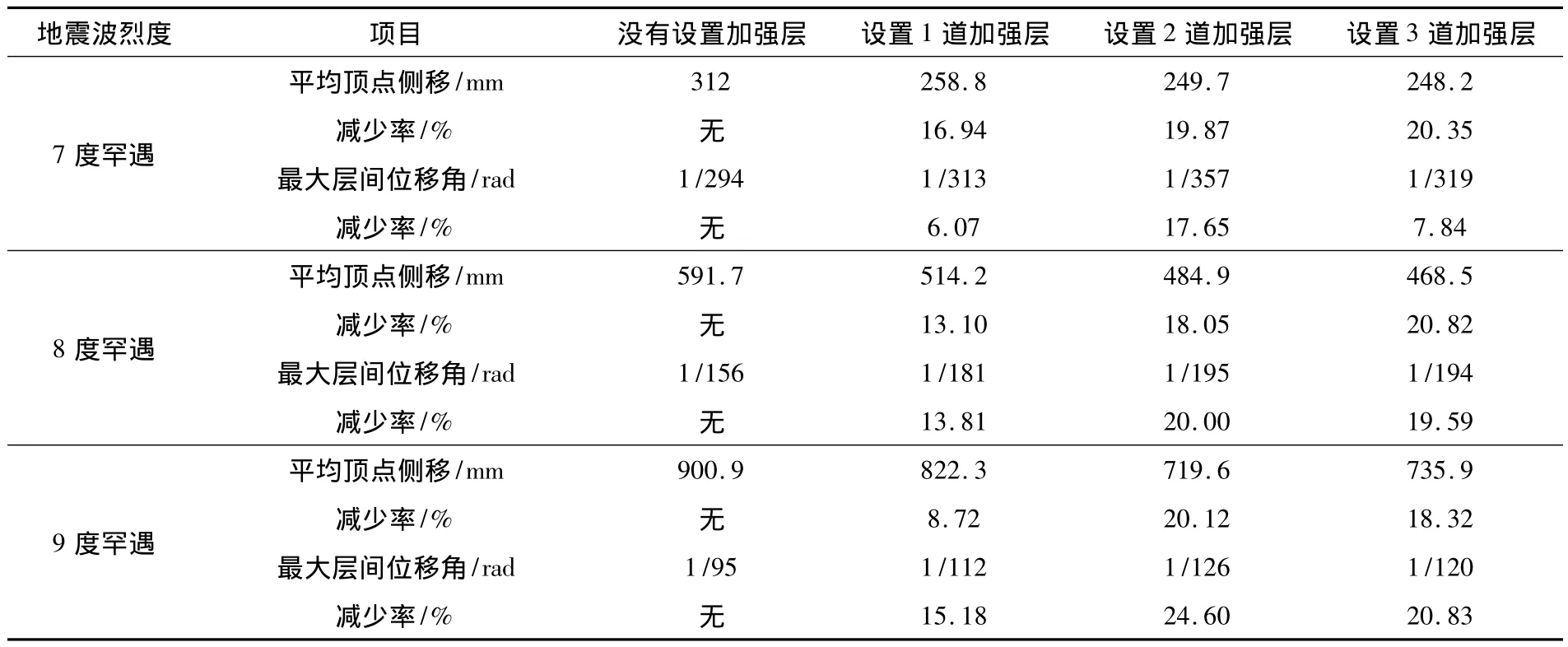
表4 4种结构在不同烈度下的位移反应Table 4 Different intensity in the four structures under displacement

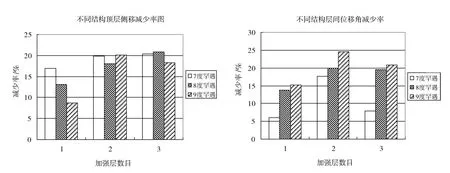
图9 设置加强层后不同结构的顶层侧移与最大层间位移角减少率对比图Fig.9 Set at different structures to strengthen the top layer of the lateral story drift and maximum reduction rate comparison chart

4.2.3 塑性铰分布

(1)7度罕遇地震波作用下4种结构基本处于弹性阶段，层间最大位移角分别为 1/294，1/313，1/357和1/319，楼层梁未出现塑性铰。

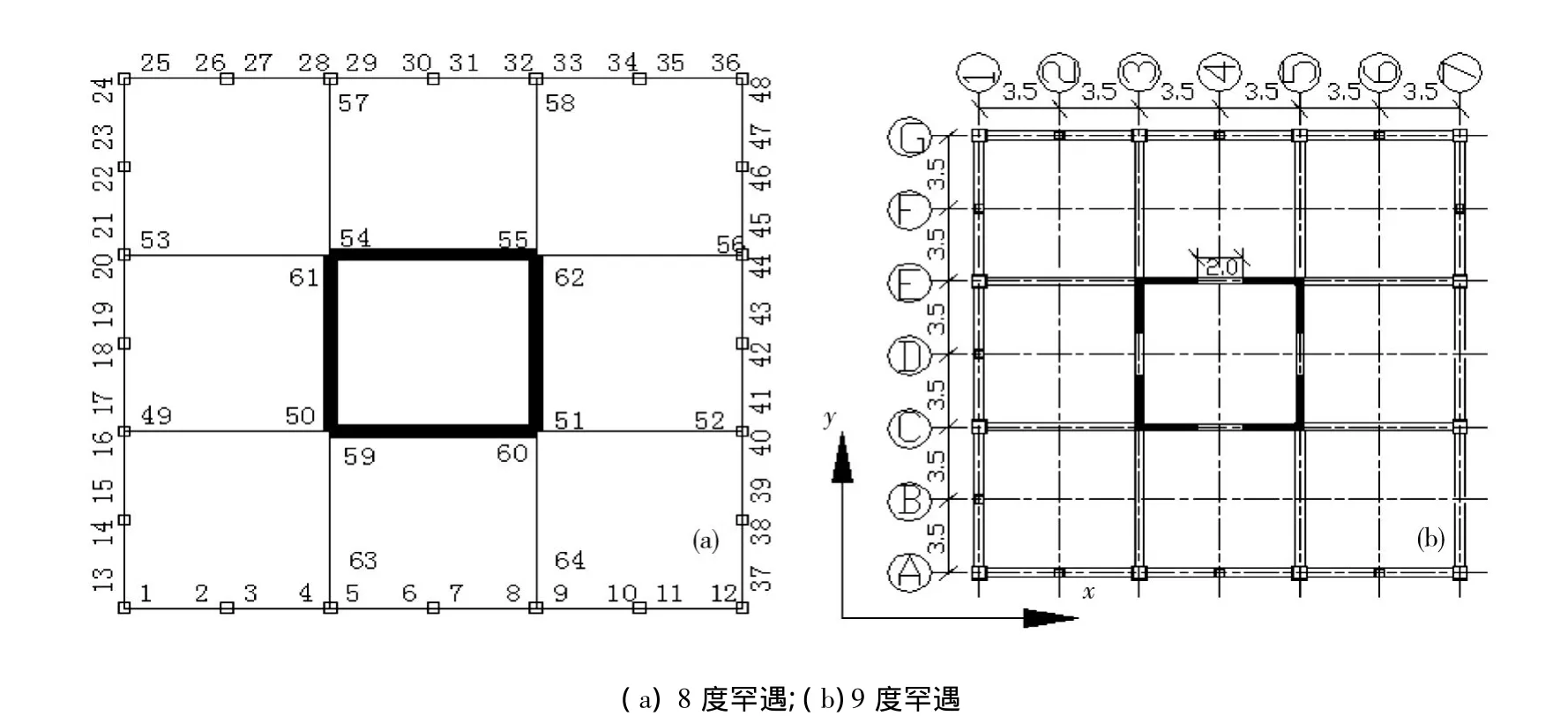
图10 塑性铰平面表示示意图Fig.10 Plastic hinge flat schematic diagram

(2)8度罕遇地震作用下，结构处于弹塑性状态，4种结构塑性铰分布情况见表5。随着加强层数目的增加，“强柱弱梁”的延性抗震体系得到很好的诠释，塑性铰不仅数目有所减少，并且塑性铰由柱端塑性铰转化为梁端塑性铰，且设置2道与3道加强层的效果并不明显。

(3)9度罕遇地震作用下，按照图10(b)的轴向将模型垂直于主方向将模型沿ACEG 4个轴向切开，可以得到各轴平面的塑性铰分部图。由于A轴与G轴、C轴与E轴的塑性铰分布基本一致，这里只描述C轴和G轴的塑性铰分布图。

表5 不同结构在8度罕遇地震作用下的塑性铰分布表Table 5 8degrees of different structures under severe earthquake the plastic hinge distribution table

图11主要是描述钢框架和核心筒之间的连梁的塑性铰与中柱塑性铰的分布情况，由图11可以看出:未设置加强层的结构22层以下的连梁均进入塑性状态，且1层和2层底柱出现塑性铰;设置1道加强道后，16层以下的连梁才进入塑性状态，且1层和2层底柱出现塑性铰;设置2道和3道加强道后，结构连梁出现少数塑性铰，底柱依然出现塑性铰。

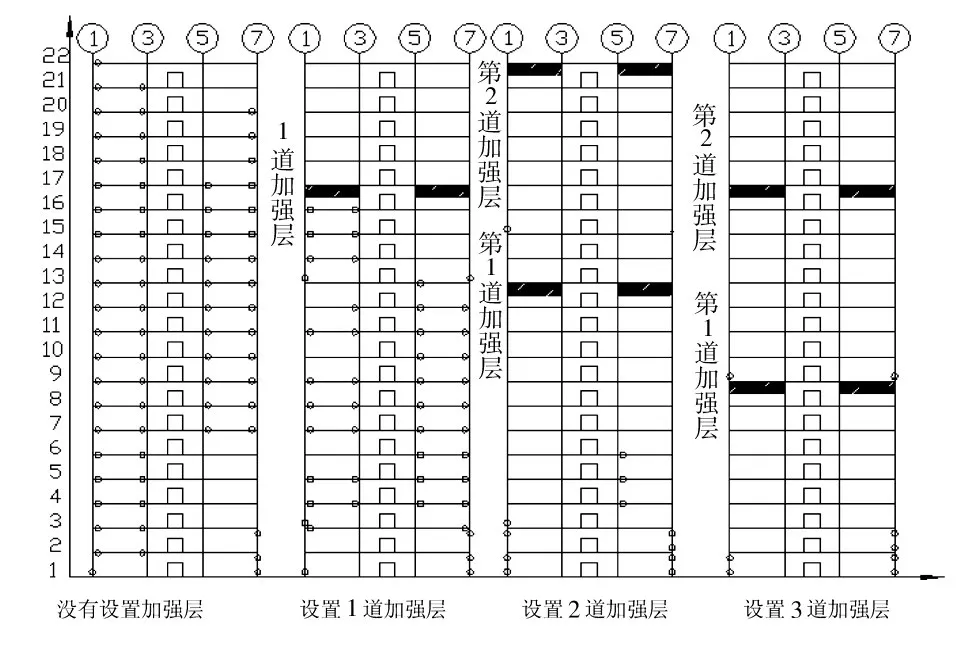
图11 C轴塑性铰分布图Fig.11 Distribution of plastic hinge axis C

图12主要是描述钢框架外围柱的塑性铰的分布情况。由图12可以看出，在没有设置加强层的结构中，18层以下的大部分梁柱都已经产生了塑性铰;设置加强层后的结构塑性铰的数量明显的减少;随着加强层数的增多，塑性铰的数量也在减少，并且塑性铰出现楼层数下降;但是设置2道加强层与设置3道加强层的结构塑性铰数目相差不大。

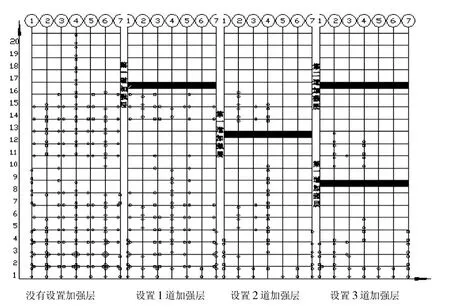
图12 G轴塑性铰分布图Fig.12 Distribution of plastic hinge axis G

5 结论

(1)加强层数目的增加使得结构刚度增加，这对降低结构前6阶的自振周期有明显的作用。

(2)结构在7度、8度和9度罕遇地震作用下设置2道加强层与设置3道加强层结构减少顶点侧移的效果相同，但是设置2道加强层在减少层间位移角的效果上明显优于设置1道与设置2道加强层。

(3)7度罕遇地震的作用下，结构处于完全弹性状态。8度罕遇地震作用下，结构处于弹塑性状态。随着加强层数目的增加，“强柱弱梁”的延性抗震体系得到很好的诠释，塑性铰不仅数目有所减少，并且塑性铰位置由柱端塑性铰转化为梁端塑性铰，且设置2道与3道加强层的效果并不明显。9度罕遇地震作用下，20层以下的大部分梁、柱已经处于塑性状态，随着加强层数目的增加，塑性铰的数目也有减少，设置2道与3道加强层的效果并不明显。

(4)设置加强层有利于更好的减少结构在地震作用下的顶层侧移和层间位移角，但是随着加强层数目增多的抗震效果不明显，设置加强层尽可能选择设置2道加强层而非多道加强层。

［1］沈蒲生.带加强层与错层高层结构设计与施工(新型高层结构系列)［M］.北京:机械工业出版社，2009.SHENG Pushen.With a strengthening layer and the split－level design and construction of high－rise structure(New series of high－rise structure)［M］.Beijing:Machinery Industry Press，2009.

［2］罗应松.带钢桁架水平加强层的钢框架－核心筒结构的受力性能与弹塑性动力时程分析［D］.长沙:中南大学，2010.LUO Yingsong.The mechanical performance and inelastic time－history analysis of steel frame－core wall structure with steel truss horizontal strengthened story［D］.Chang-Sha:Central South University，2010.

［3］李云贵.多层、高层建筑结构弹塑性动力、静力分析［J］.建筑结构学报，2002，10(5):56 －62.LI Yungui.Elastic－plastic dynamic and static analysis of building structures［J］.Journal of Building Structures，2002，10(5):56 －62.

［4］赵忠虎，张过庆.压弯构件恢复力模型骨架曲线的研究［J］.工业建筑，2007，37(9):73 －76.ZHANG Zhongfu，ZHANG Guoqing.Flexure and compression restoring force model of skeleton［J］.Industrial Construction，2007，37(9):73 －76.

［5］辛学忠，蒋丽忠，曹华.钢一混凝土连续组合梁的恢复力模型［J］.建筑结构学报，2006，27(1):83 －89.XING Xuezhong，JIANG Lizhong，CAO Hua.Steel concrete composite beams with a restoring force model［J］.Journal of Building Structures，2006，27(1):83 －89.

［6］尚晓江，邱峰，赵海峰.AWSYS结构有限元高级分析方法与范例应用［M］.北京:中国水利水电出版社，2005.SHANG Xiaojiang，QIU Feng，ZHAO Haifeng.The premium analysis method of ANSYS finite element and paradigm application［M］.Beijing:Chinese Water Conservancy and Water Electricity Press，2005.

［7］陈精一，蔡国忠.电脑辅助工程分析－ANSYS使用指南［M］.2001.CHEN Jinyi，CAI Guozong.Computer aided engineering analysis－ ANSYS guide［M］.2001.

［8］祝效华.ANSYS高级工程有限元分析范例精选［M］.北京:电子工业出版社，2004.ZHU Xiaohua.ANSYS finite element analysis of advanced engineering sample selection［M］.Beijing:Electionics Industuy Press，2004.

［9］GB 50011—2001，建筑抗震设计规范［S］.GB 50011—2001，Code for seismic design of buildings［S］.

［10］方德平，王全凤.Wilson－θ法两种积分格式的稳定性探讨［J］.计算力学学报，2008，25(4):539 －541.FANG Deping，WANG Quanfeng.Wilson－θ method of two points，the stability［J］.Chinese Journal of Computational Mechanics，2008，25(4):539 －541.

［11］SHI Dongyang，LIANG Hui.Superconvergence analysis of Wilson element on anisotropic meshes［J］.Applied Mathematics and Mechanics(English Edition)，2006，27(1):119－125.

［12］杨志勇，黄吉锋.弹性、弹塑性时程分析法在结构设计中的应用［J］.建筑结构，2007，9(1):29 －32.YANG Zhiyong，HUANG Jifeng.Elastic，nonlinear time history analysis in structural design［J］.Journal of Building Structures，2007，9(1):29 －32.