单元板式轨道脱空伤损识别的柔度曲率特征值法
赵坪锐,徐天赐,刘卫星,屈超广,毕澜潇,丁晨旭
(1.西南交通大学高速铁路线路工程教育部重点实验室,四川 成都 610031;2.西南交通大学土木工程学院,四川成都 610031)
我国自主研发的CRTS Ⅲ型板式无砟轨道具有结构简单、施工方便、可维修性强等特点.随着高速铁路运营时间的增加,在列车动荷载与环境因素作用下,板式轨道结构关键部件出现多种形式病害,常见病害为轨道板与自密实混凝土层间离缝,且当离缝高度较大时产生板底脱空伤损,改变轨道结构的传力特性,影响轨道系统的平顺性和耐久性,进而降低高速列车的行车舒适性和安全性[1].因此寻找合理的无损检测方法快速识别无砟轨道结构伤损是十分重要的.
针对混凝土结构伤损的无损检测方法主要分为识别伤损有无的整体检测方法(如利用基于结构振动的频率[2-3]、振型[4-5]、应变[6-7]及刚度、柔度矩阵[8-9]等指标)和可进一步识别伤损特征的局部检测方法(如射线法[10]、超声波法[11]、超声导波法[12]、冲击回波法[13]等).国内外学者利用以上方法取得了一系列有价值的研究成果.Kim 等[14]基于伤损前后结构固有频率和模态应变能的变化实现对桥梁结构中裂缝伤损的定位及尺寸预估.Dawari 等[15]通过桥梁结构的有限元模型分析了模态曲率对结构伤损的敏感度,并利用模态曲率差指标对钢筋混凝土桥蜂窝伤损进行识别和定位.而用于伤损识别的差值指标需要完整结构的动力响应作为基准量,针对无砟轨道结构实际中无法采集可为长线路提供基准的参数.Wu等[16]研究了空间小波变换对悬臂梁裂缝伤损识别的适用性,并结合梁结构在静态位移下的裂缝检测试验进行验证.李永梅等[17]研究了伤损对简支梁结构柔度矩阵的影响,并利用其敏感度指标的变化实现了对结构伤损的识别和定位.现有检测手段多针对桥梁等一维结构,而轨道结构为多层混凝土结构,无法仅用一维指标进行伤损识别.针对二维结构,马俊、陈立等[18-19]从理论推导、数值仿真、模型试验方面验证了板壳结构的柔度矩阵比值对结构伤损定位和伤损程度识别的准确性.Nie 等[20]提出一种基于实测振动信号重构多维相空间几何变化的CPST(changes of phase space topology)指标,并应用于钢筋混凝土连续板结构的伤损识别,试验结果表明,该指标可在单个或最少数量测试点的工况下实现对连续板结构伤损有无的检测,且相比于传统基于模态的伤损指标,该指标对结构伤损的敏感性更强.实际中多层混凝土的轨道结构比普通板壳结构受力更复杂,伤损指标更难反映实际结构伤损,需进一步寻找新的检测手段.在将伤损指标应用于试验或工程实践时,检测手段需符合伤损结构的工程特点.Xu 等[21]结合薄板振动微分方程提出自定伤损指标,通过机电振动器和激光采集系统实现小尺寸铝板平面测点的低阶振动模态位移获取,验证了伤损识别准确性.Xu 等[22]根据高斯曲率理论,利用伤损轨道结构振型曲率的变化特点识别轨道板底脱空,并通过双层板-弹簧有限元模型和试验进行验证;在试验时通过单点激励多点采集的方式收集结构振动信号,采用接地技术及移动平均滤波技术进行实测数据降噪,得到轨道板的前4 阶模态参数,实现板底脱空伤损的识别;在工程实践中,传统轨道结构表面设点的测试方法可获取离散轨道板的动力响应,且轨道结构的高阶模态较难被激励,相关参数难以测得,因此为实现工程中实时检测,需提出一种可进行连续快速自动检测的伤损指标.
基于现有检测手段的不足,本文针对单元板式无砟轨道板底脱空伤损结构,建立4 层实体有限元模型,利用模态分析结果获取结构柔度矩阵,并结合高斯曲率和相关降噪数据处理的理论构造柔度曲率特征值这一伤损识别指标.同时为验证该方法在工程实践中的可行性,构建反映非伤损区域内不规则突起对伤损定位影响的准确性指标和识别伤损范围的有效性指标,得到合理的测点密度.最后通过建立不同伤损工况研究了该方法在无砟轨道多层混凝土结构伤损识别中的适用性和应用范围.该方法无需完整结构的动力基准,且仅需伤损结构的第1 阶模态参数即可实现对单一轨道板底脱空伤损的识别,目前虽无法实现连续自动检测,但可为实现对单元板式无砟轨道结构隐蔽伤损的识别提供一定理论依据.
1 理论基础
1.1 柔度矩阵
柔度矩阵是对轨道板振动振型和频率的综合特征的体现,把轨道板上表面结构划分为 (a−1)×(b−1) 个单元,节点共n个(n=a×b),通过轨道结构的模态分析,获取第m阶 (m=1,2,···,M)模态下经质量归一化处理后的每个节点位移或转角数据,构成第m阶模态下质量归一化振型向量 φm为

式中:φkm为第m阶轨道板上表面第k个节点的模态位移,k≤n.
取伤损结构前M阶振型构造的柔度矩阵[23-24]为

式中:ωm为伤损结构的第m阶模态频率.
设Ce为F中第e列最大值,得到过渡矩阵为

将F1内各元素按轨道板上表面节点分布方式进行排布,即可构造柔度最大值矩阵F2为

1.2 高斯曲率
在计算轨道板柔度曲率时,会涉及x、y两个方向的柔度曲率值,由微分几何知识可知,高斯曲率可以综合反应板状结构两个方向上的曲率,设振型曲面上任意一点的两个主曲率为f1和f2,则其乘积称为曲面在这一点的高斯曲率[20],如式(5)所示.

式中:Kij为曲面z上离散点zi,j(横坐标i,纵坐标j)的高斯曲率;r、s、t、p、q分别为曲面z=z(x,y)对x、y的偏导,可利用差分法分别计算,如式(6)所示.

式中:Δx、Δy分别为差分计算中离散数据沿x、y轴的距离.
2 算例数值计算
2.1 模型建立
利用有限元软件对CRTS Ⅲ型板式轨道结构进行建模分析,轨道板、自密实混凝土和底座板采用SOLID 45实体单元模拟,地基采用COMBIN14线性弹簧单元模拟,轨道板底脱空伤损采用实体单元间布尔运算来模拟,且厚度方向全部脱空.约束底座板和自密实混凝土层4 个侧面的横、纵向位移,对地基弹簧底面节点进行全约束.轨道板上表面尺寸为4.8 m×2.4 m,网格划分间距为0.05 m,其他有限元模型参数见附加材料表S1.
2.2 伤损轨道结构数值模拟
单处伤损工况下,设置边长d为0.4 m 的方形脱空区域,如图1 所示,脱空中心点坐标为(1.2 m,1.2 m).对伤损轨道结构进行模态分析后,在轨道板上表面选取l=0.20 m(Δx=Δy=l) 作为x、y轴方向上的测点密度提取各阶模态位移(合理测点密度范围讨论见第3 节),得前10 阶的模态频率和相应的模态质量归一化后节点振型向量.

图1 轨道板底单伤损区域及测点布置(单位:m)Fig.1 Single-damaged area of slab bottom and measuring point layout (unit:m)
利用MATLAB 编程软件对模态数据进行计算,可得单处伤损的轨道板柔度矩阵,前1 阶的柔度矩阵如附加材料图S2.可知柔度在伤损区域内有微突起,并不明显,工程中无法仅靠柔度矩阵进行脱空伤损识别.
结合高斯曲率理论可得轨道板的柔度曲率矩阵.由式(2)可知高阶模态数据对柔度矩阵的构造影响较小,为寻找合适的模态阶数截断数,构造前1 阶、前3 阶、前10 阶的柔度曲率矩阵,结果如图2 所示.由图可知:前1 阶柔度曲率在脱空伤损区域存在较突出的峰值,可初步判断脱空伤损位置;前3 阶和前10 阶的柔度曲率无法进行伤损识别.因此采用前1 阶柔度曲率识别轨道板底脱空伤损,避免了实际轨道结构高阶模态较难激励、数据难以测得的问题.前1 阶柔度曲率三维阴影图和平面等高线如图3所示.

图2 不同模态截断数时轨道板柔度曲率Fig.2 Flexibility curvature of track slab at different modal truncations

图3 单伤损轨道板的前1 阶柔度曲率Fig.3 First-order flexibility curvature of track slab with single damage
由图3(b)平面等高线图可得,柔度曲率矩阵的峰值出现在脱空伤损区域,但在非伤损区域存在不规则突起会对伤损识别带来干扰,因此需要对柔度曲率矩阵做降噪处理.处理方法为对柔度曲率矩阵中的每个元素进行平方计算,并归一化处理为柔度曲率特征值,结果如图4 所示.
由图4(b)平面等高线图可以看出,柔度曲率特征矩阵仅在伤损区域内存在明显突起,可准确识别脱空伤损,而非伤损区域内不规则突起均被过滤,不再干扰伤损识别.为探究其伤损定位的准确性,在平面等高线图内标出伤损区域并提取柔度曲率特征值进行观察,结果如图5 所示.

图4 CRTS Ⅲ型板单伤损轨道板的柔度曲率特征矩阵Fig.4 Flexibility curvature eigenvalue matrix of CRTS Ⅲballastless track slab with single damage
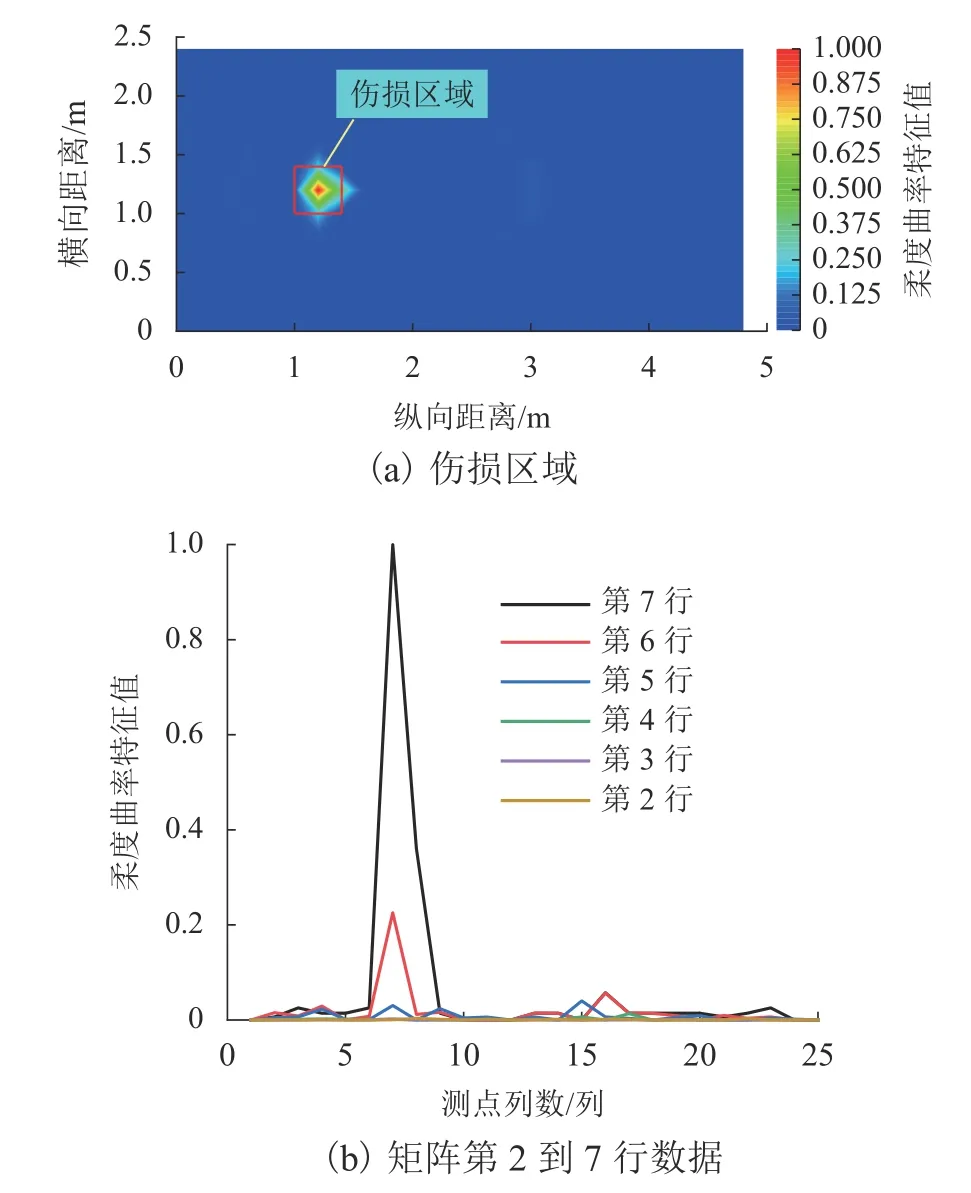
图5 CRTS Ⅲ型板中柔度曲率特征矩阵单伤损识别定位Fig.5 Identification and localization of single damage in CRTS Ⅲ ballastless track slabby flexibility curvature eigenvalue matrix
由图5 可得,在伤损区域内柔度曲率特征值发生了较大变化,且峰值在柔度曲率特征矩阵中的位置为第7 列第7 行,对应坐标为 (1.2 m,1.2 m),峰值位置与伤损区域中心相吻合.相同工况下CRTS Ⅰ型板式无砟轨道伤损结构的柔度曲率特征矩阵如图6所示,利用该伤损指标对板底脱空伤损的识别定位如图7 所示.因此,该指标可准确用来识别、定位两种单元板式轨道板底单处脱空伤损.

图6 CRTS Ⅰ型板单伤损轨道板的柔度曲率特征矩阵Fig.6 Flexibility curvature eigenvalue matrix of CRTSⅠballastless track slab with single damage
轨道板底多处伤损工况较单处伤损更复杂,为研究该方法的适用性,在此算例中建立板底两处脱空伤损模型,且模型数据提取及降噪方法与单处伤损模型算例中相似,不再赘述.两处伤损区域及测点分布见附加材料图S2,分析结果见附加材料图S3、S4.可知该工况下柔度曲率特征矩阵仅在两处伤损区域内存在明显突起,且峰值位置与伤损区域中心吻合,因此该方法可准确用来识别、定位两种单元板式轨道板底多处脱空伤损.
比较该指标对CRTSⅠ及CRTS Ⅲ型两种单元板式轨道的伤损识别结果发现,轨道板底支承材料是CA 砂浆或自密实混凝土,用该标均可进行有效的伤损识别,说明该法主要针对脱空伤损,即识别板底是否存在支承,支承材料的力学性能(主要为弹性模量)对伤损识别效果的干扰较小.
3 测点密度调整
3.1 计算工况
采用不同密度的测点数据时,对由差分计算得到的柔度曲率影响较大,为研究测点密度对该方法识别效果的影响,选l=0.05,0.10,0.15,0.20,0.30,0.40 m 6 种测点密度工况提取模态分析结果,构造柔度曲率特征矩阵进行比较,部分结果如图8,其余结果见附加材料图S5.
由图8 可得,由于轨道实体结构的复杂性和差分计算的特点,随着l/d比值的增大,非伤损区域内噪声会逐渐降低,减小对伤损识别的干扰,同时平面图中表示伤损区域的菱形面积在逐渐增加,甚至大于实际伤损区域,无法反映实际伤损范围.因此探寻合理的测点密度是十分必要的.
3.2 指标构造
在不同测点密度工况下,构建反映非伤损区域内不规则突起对伤损定位影响的准确性指标IDC(index reflecting difference calculation)和识别伤损范围的有效性指标IRE(index reflecting the recognition effect).
3.2.1 IDC
归一化处理后的柔度曲率特征矩阵峰值为1.0,且均在伤损区域内,因此不同工况下非伤损区域内最大柔度曲率特征值即代表非伤损区域内噪声对伤损定位的干扰,构造无量纲 I DC为

式中:tc为反映伤损识别精度的阈值.
如图9 为l/d=0.250 时特征值t提取的示意,在非伤损区域内选取最高点A,并将其柔度曲率特征值数值赋值于t,即t为在不同测点密度工况下非伤损区域内最大柔度曲率特征值.
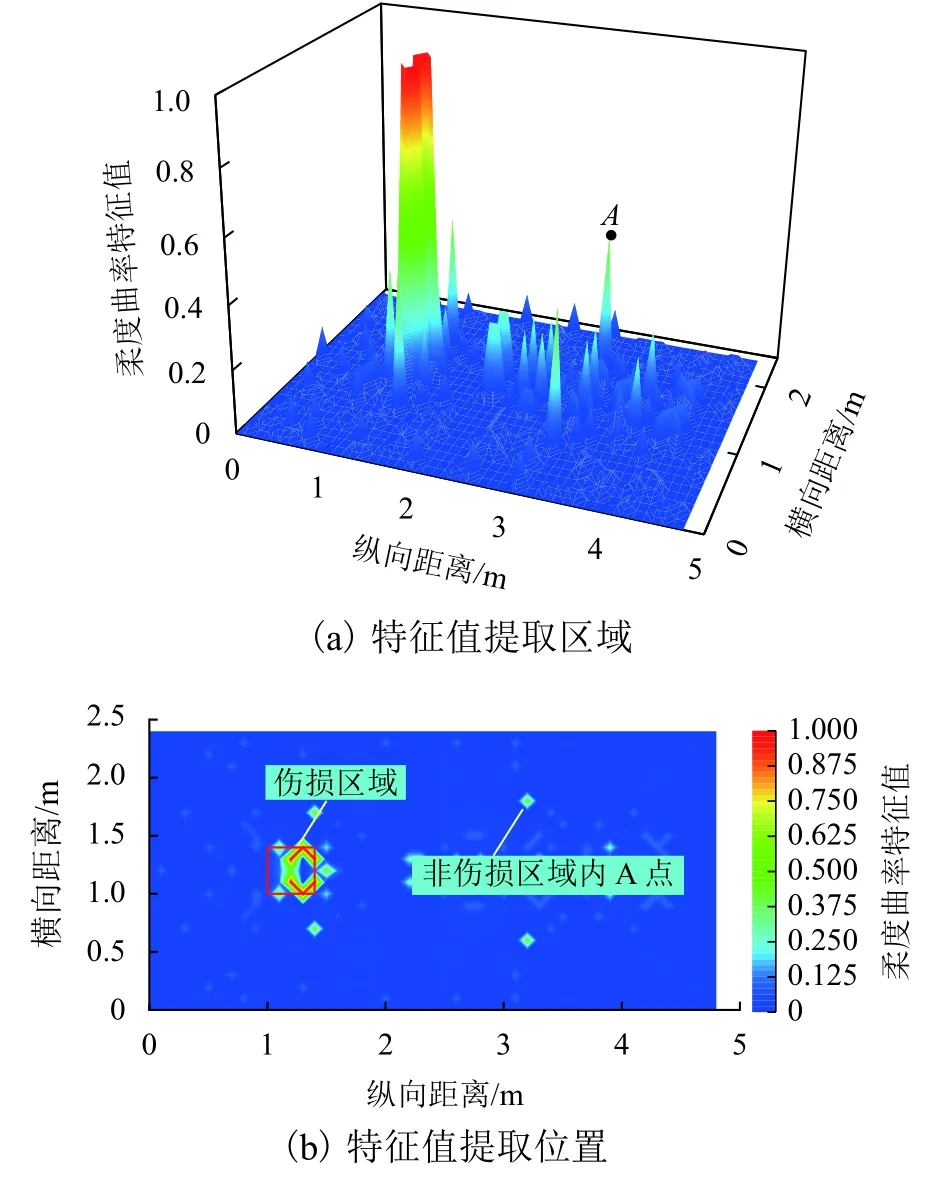
图9 测点密度 l=0.10 m 时特征值 t 提取示意Fig.9 Eigenvalue t extracted with density of measuring points l=0.1 m
计算不同工况下的柔度曲率特征矩阵.当fIDC≥1.0时,该工况下非伤损区域内突起明显、噪声干扰较大,会影响伤损定位的准确性;当 0 3.2.2 IRE 采用识别伤损范围和实际伤损范围之间二维相关性系数表示在不同测点密度工况下伤损范围识别的有效性.相关性系数 ρ为[21] 式中:Nx和Ny分别为轨道板上表面在x轴和y轴方向上测点个数;hi,j为第i行第j列测点处自密实混凝土厚度;Ci,j为第i行第j列测点处柔度曲率数值. ρ 的数值范围为[0,1.0],且 ρ越接近于1.0,二者间线性关系越密切,ρ越接近于0,二者间线性相关越弱.构造无量纲IRE为 式中:ρc为对伤损区域识别有效性的接受程度阈值. 当fIRE≥1.0时,表示采用该测点密度进行伤损范围识别的效果不佳,无法较准确的识别伤损范围;当0 通过构造两个参数指标,仅当 0 图10 IDC 和IRE 计算结果Fig.10 IDC and IRE values 同时为研究在不同脱空尺寸下,该测点布置方式的可用范围,建立更大脱空尺寸的轨道结构有限元模型进行计算.以板底0.8 m×0.8 m 的脱空伤损为例,结果如图11 所示,可知选取l/d=0.250即l=0.20 m时伤损识别效果更好,尽管随着脱空尺寸的增大,效果最佳的l/d比值在减小,但测点密度l均为 0.20 m,因此针对边长不小于0.4 m 的脱空伤损,均可选取l=0.20 m进行轨道板底脱空伤损识别研究. 图11 两种脱空尺寸下IDC 和IRE 计算结果Fig.11 IDC and IRE values for two debonding sizes 采用柔度曲率特征矩阵可以有效识别轨道板底的单处和多处脱空伤损.为进一步研究在不同尺寸伤损区域工况下轨道板柔度曲率的变化规律,确定柔度曲率特征矩识别范围,分别建立脱空边长d为0.3、0.4、0.5、0.6、0.7 m 5 种工况轨道单伤损结构的有限元模型进行分析. 5 种工况下柔度曲率特征矩阵峰值均为1.0,无法研究其变化规律,因此选取柔度曲率矩阵作为研究对象,观察每种工况下柔度曲率矩阵中最大绝对值随伤损尺寸的变化规律,结果如图12 所示. 由图12 可得,5 种工况下轨道板柔度曲率最大绝对值不同,其值随脱空尺寸变大而增加,两者之间呈基本线性关系,且脱空尺寸越大,轨道板柔度曲率最大绝对值增加得越快. 图12 轨道板脱空尺寸与柔度曲率关系Fig.12 Relationship between debonding size and flexibility curvature oftrack slab 为研究利用柔度曲率特征矩阵可有效识别的伤损尺寸范围,计算5 种工况下轨道板的柔度曲率特征矩阵,并进行比较,结果见附加材料图S6. 由分析结果的可视化图形可得,5 种脱空伤损尺寸下的柔度曲率特征矩阵在伤损处均有峰值存在,但当伤损区域边长为0.3 m 时,非伤损区域内最大噪声大于0.2,无法进行伤损识别定位;而当伤损区域边长大于0.3 m 时,均可准确地进行伤损识别定位.因此,当脱空区域边长大于0.3 m 时,可利用柔度曲率特征矩阵进行准确的伤损识别和定位. 结合4.1 与4.2 分析可知,脱空伤损会改变轨道板柔度曲率,柔度曲率最大绝对值随脱空尺寸变大而增加,二者呈基本线性关系,且不同脱空尺寸下可视化图形中的有效伤损区域大小也不同,可进行伤损面积的识别. 本文通过板式无砟轨道板底脱空结构的有限元计算,将结构的模态分析结果与柔度矩阵、高斯曲率等数据处理手段相结合进行研究,主要得到以下结论: 1)提出柔度曲率特征值伤损指标,仅根据伤损的第一阶模态振幅,采用柔度曲率特征矩阵可有效对两种单元板式无砟轨道板底单处和多处脱空伤损进行识别和定位. 2)针对轨道板底大于0.4 m×0.4 m 的脱空伤损,采用测点密度为0.2 m 计算柔度曲率特征值时,有利于降低非伤损区域内不规则突起对伤损定位准确性的影响、提高伤损范围识别的有效性. 3)当轨道板底脱空伤损区域边长大于0.3 m 时,可利用柔度曲率特征矩阵准确进行伤损识别和定位. 4)轨道板柔度曲率最大绝对值随脱空尺寸变大而增加,二者基本呈线性关系,结合柔度曲率特征值的可视化图形可进行伤损面积识别. 备注:附加材料在中国知网本文的详情页中获取.

3.3 测点密度选取


4 识别应用范围
4.1 柔度曲率的变化规律

4.2 伤损定位的尺寸范围
5 结 论

