L-模糊上近似的唯一公理刻画

李令强

1.湖南大学 数学与计量经济学院，长沙 410082

2.聊城大学 数学科学学院，山东 聊城 252059

L-模糊上近似的唯一公理刻画

李令强

1.湖南大学 数学与计量经济学院，长沙 410082

2.聊城大学 数学科学学院，山东 聊城 252059

1 引言

粗集理论是Pawlak教授于1982年提出的一种能够定量分析处理不精确、不完整信息与知识的数学工具[1]。Pawlak粗集是基于等价关系的，但是等价关系要求过高，因此，人们把等价关系放宽为一般的二元关系或者覆盖，或者进一步把二元关系或者集合模糊化，研究了各种各样的广义粗集[2-4]，模糊或者更一般的L-模糊粗集[5-10]，其中 L为某个格结构。

公理化是研究粗集的重要方式。设 X为任意论域，P(X)为其幂集。一般来说，公理化就是探寻使抽象算子 f∶P(X)→P(X)等价于由某二元关系（覆盖）定义的上、下近似算子的条件。文献[11]和文献[12]分别研究了关系和覆盖粗集的公理系统，而文献[6-7，13]研究了模糊或者更一般的L-模糊粗集的公理系统。值得注意的是上述公理系统都有多个公理组成。最近，受上近似算子和Kuratowski闭包算子的相似性和后者可以通过唯一公理刻画的启发，文献[14]给出了粗集和模糊粗集的上近似算子的唯一公理刻画。这有助于人们从多方面、多视角出发来研究粗集理论。

近年来，因为具有一定的逻辑意义，剩余格值L-模糊粗集理论[5，7-8，10]备受关注。本文的目的是借鉴文献[14]的方式给出剩余格值L-模糊粗集上近似算子的唯一公理刻画。本文中总假设L=(L,∨,∧,⊗)是完备剩余格[7，14]，并假设读者熟悉其性质。设X为非空论域，记X的所有L-模糊集之集为FL(X)，则L上的运算⊗,∨,∧可以逐点传递到FL(X)上。记L的最大（小）元为1（0）。任取λ∈L，仍用λ表示取常值λ的L-模糊集，任取A∈FL(X)，用λA表示L-模糊集λA(x)=λ⊗A(x)。对任意x∈X，λ≠0，用λ/x表示L-模糊集λ/x(y)=λ若y=x否则λ/x(y)=0。

2 经典上近似算子的公理化

设R为论域X上的二元关系，（1）若任取x∈X有xRx，则称R为反身的；（2）若xRy蕴涵着 yRx，则称R为对称的。任取x∈X，记rR(x)={y|xRy}。对任意A∈P(X)，分别称

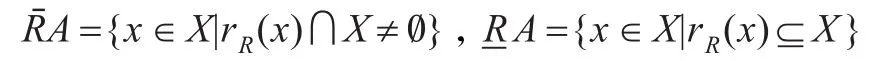
为A的上、下近似。对任意A∈P(X)，仍用A来记及其特征函数，即∀x∈X，若x∈A则A(x)=1否则A(x)=0。任取A，B∈P(U)，称值：

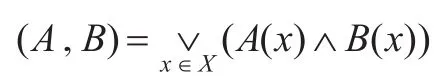
为A与B的内积。

设 f∶P(X)→P(X)为任意算子，定义其逆算子 f-1∶P(X)→P(X)为：对任意A∈P(X)

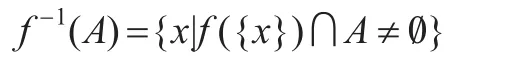
文献[14]得到了上近似算子的如下唯一公理刻画：

（1）存在 X上唯一的二元关系 R使得对任意A∈P(U)有 f(A)=当且仅当对任意 A，B∈P(X)有(A，f(B))=(B，f-1(A))。

（2）存在 X上唯一的反身的二元关系R使得对任意 A∈P(U)有 f(A)=当且仅当对任意 A，B∈P(X)有(A，B∪f-1(B))=(B，f(A))。

（3）存在 X上唯一的对称的二元关系R使得对任意 A∈P(U)有 f(A)=当且仅当对任意 A，B∈P(X)有(A，f(B))=(B，f(A))。

本文的主要目的是将上述结论推广到L-模糊粗集的情形。

3 L-模糊上近似算子的公理化

设R为论域 X上的L-模糊关系，即 X×X上的L-模糊集。（1）若任取 x∈X有R(x，x)=1，则称R为反身的；（2）若R(x，y)=R(y，x)，则称R为对称的。任取x∈X，定义 X上的L-模糊集lR(x)为：lR(x)(y)=R(y，x)。

任取A∈FL(X)，称

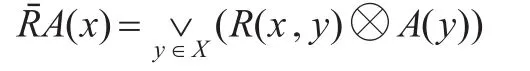
为A的L-模糊上近似。它具有如下性质[8]。设A,B∈FL(X)，λ∈L：

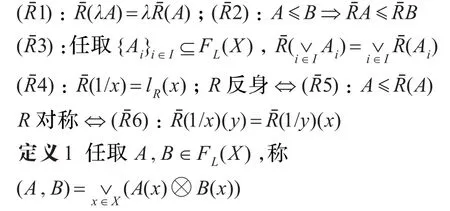
为A和B的内积。文献[5]称之为A和B的相关度。

引理1任取A，B，Ai(i∈I)∈FL(X)，有

（1）(A，0)=0，（2）(A，B)=(B，A)，（3）(A，Ai)=(A，Ai)，（4）若 B≤C，则(A，B)≤(A，C)，（5）若任取C∈FL(X)有(C，A)=(C，B)，则A=B。

证明（1）～（4）在文献[5]中已经指出，仅证（5）。事实上，任取x∈X，令C=1/x，则

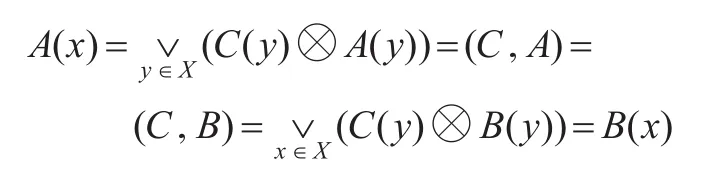
由x的任意性得A=B。

定义2设 f∶FL(X)→FL(X)为任意算子，称算子 f-1∶FL(X)→FL(X)

为 f的逆算子。

注记1当L={0，1}时，⊗=∧，L-模糊集退化为分明集。则

上式说明，定义的逆算子是分明情形的恰当推广。引理2设存在X上的L-模糊关系R使得 f=，则：

（1）f-1=，其中 R-1为 R的逆关系，定义为R-1(x，y)=R(y，x)。

（2）若R对称则 f=f-1。

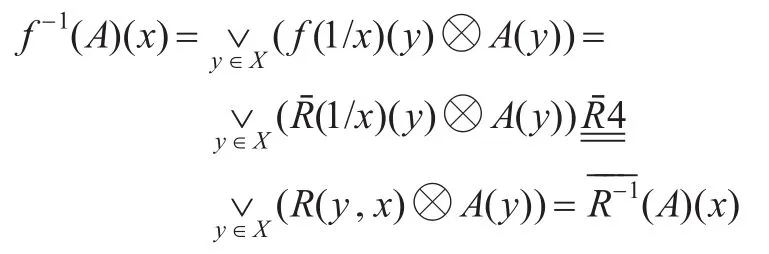
故（1）成立。若R对称则R=R-1，故由（1）得（2）。

以下，设 f∶FL(X)→FL(X)为任一算子。

（A）∀A，B∈FL(X)，(A，f(B))=(B，f-1(A))

1.2.2 问卷考评 量表编制基本完成后，通过预调查考察量表的信、效度，信度系数值为0.934，大于0.9，说明研究数据信度质量很高。KMO值用于判断是否有效度，KMO值为0.918，大于0.6，意味着数据具有效度。由信度、效度检验可知，该量表具有较好的信度和效度。针对预调查发现的问卷不足之处，进行修正、完善，以便能准确、可靠地获得调查所需的信息。

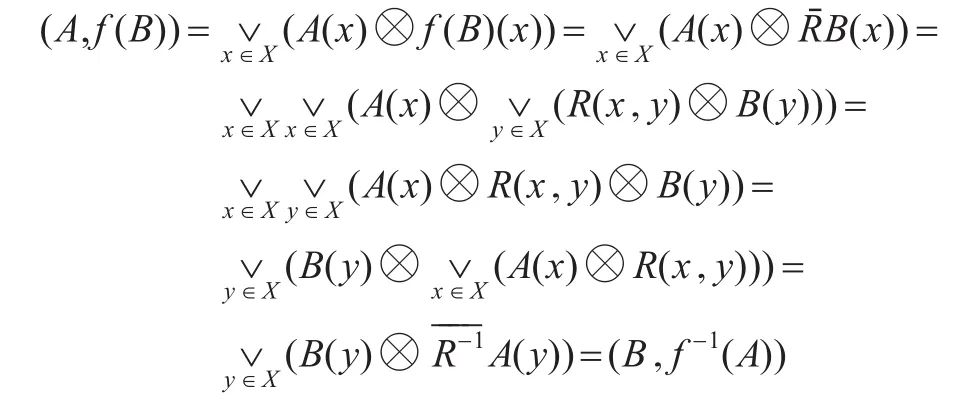
上式说明若R为L-模糊关系，则

充分性：设 f满足（A），先证 f满足：

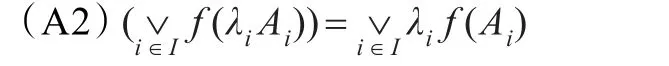
其中 I为任意指标集，{Ai}i∈I⊆FL(X)，{λi}i∈I⊆L。事实上任取B∈FL(X)，由引理1及条件（A）得：

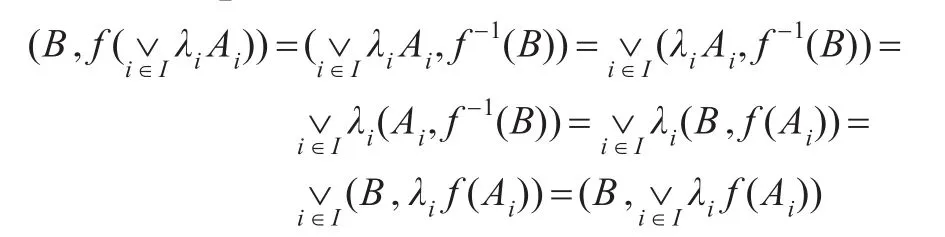
由B的任意性知条件（A2）成立。定义X上的L-模糊关系如下：

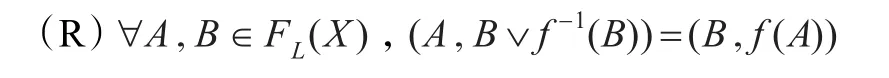
故条件（R）成立。

充分性：设f满足（R），由引理1得，任取C∈FL(X)有：

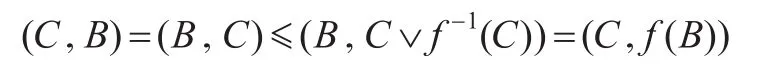
这意味着B≤f(B)。特别的，任取x∈X有 f(1/x)≥1/x，从而

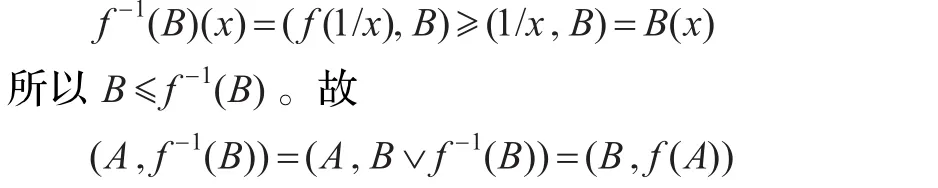
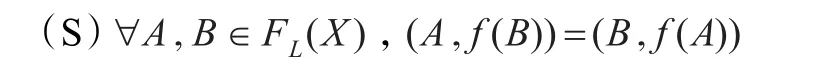
证明 必要性：设R是对称的（从而R=R-1）且 f=，由（A1）知：

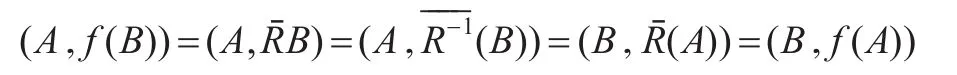
所以性质（S）成立。

充分性：设 f满足（S），下证 f满足（A2）。事实上任取B∈FL(X)，由引理1及条件（S）得：

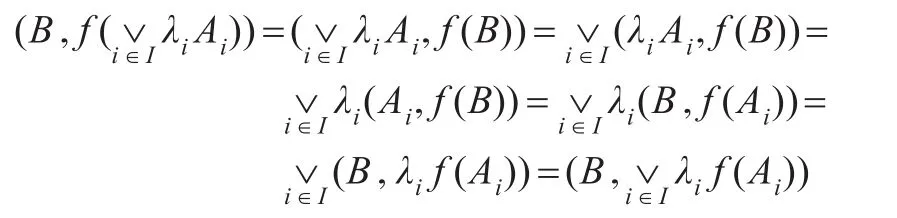
由A的任意性知条件（A2）成立。定义X上的L-模糊关系R如下：任取R(x，y)=f(1/y)(x)，类似于定理1可证=f。下证R是对称的。由（S）得：

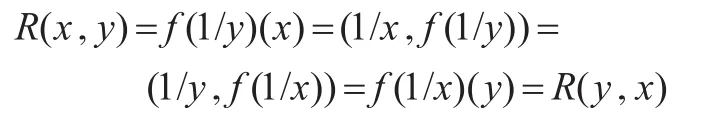
4 结束语

本文可以看做对文献[14]中部分结果的推广和深化。相较于文献[14]，本文的意义在于：（1）所取值格不同，文献[14]中L为单位区间，本文中L为剩余格；（2）文献[14]研究经典粗集的上近似时，抽象算子 f的逆算子f-1起到了至关重要的作用，但是文献[14]并未定义模糊算子的逆算子，故而模糊粗集的相应结论就无法呈现，本文弥补了这一缺憾。

[1]Pawlak Z.Rough set[J].International Journal of Computer and Information Sciences，1982，11：341-356.

[2]Yao Y Y.Relational interpretations of neighborhood operators and rough set approximations operators[J].Information Sciences，1998，111：239-259.

[3]Qin K Y，Yang J L，Pei Z.Generalized rough sets based on reflexive and transitive relations[J].Information Sciences，2008，178：4138-4141.

[4]Zhu William.Relationship between generalized rough sets based on binary relation and covering[J].Information Sciences，2009，179：210-225.

[5]Chen X Y，Li Q G.Construction of rough approximations in fuzzy setting[J].Fuzzy Sets and Systems，2007，158：2641-2653.

[6]Liu G L.Generalized rough sets over fuzzy lattices[J].Information Sciences，2008，178：1651-1662.

[7]She Y H，Wang G J.An axiomatic approach of fuzzy rough sets based on residuated lattices[J].Computers and Mathematics with Applications，2009，58：189-201.

[8]李令强，金秋，孙守斌，等.多值近似空间的上下近似诱导的拓扑结构[J].系统科学与数学，2012，32（2）：226-236.

[9]王莉，李令强，孟广武，等.区间值模糊近似空间的拓扑结构[J].计算机工程与应用，2012，48（13）：44-47.

[10]Ma Z M，Hu B Q.Topological and lattice structures of L-fuzzy rough sets determined by lower and upper sets[J]. Information Sciences，2013，218：194-204.

[11]Yao Y Y，Lin T Y.Generalization of rough sets using modal logic[J].International Journal of Intelligent Automation and Soft Computing，1996（2）：103-120.

[12]Zhang Y，Luo M.On minimization of axiom sets characterizing covering-based approximation operators[J].Information Sciences，2011，181：3032-3042.

[13]Mi J S，Zhang W X.An axiomatic characterization of a fuzzy generalization of rough sets[J].Information Sciences，2004，160：235-249.

[14]Liu G L.Using one axiom to characterize rough set and fuzzy rough set approximations[J].Information Sciences，2013，223：285-296.

[15]Hájek P.Metamathematics of fuzzy logic[M].Dordrecht：Kluwer Academic Publishers，1998.

LI Lingqiang

1.College of Mathematics and Econometrics,Hunan University,Changsha 410082,China
2.School of Mathematics Science,Liaocheng University,Liaocheng,Shandong 252059,China

By the notion of inner products of L-fuzzy sets,this paper uses only one axiom to describe the upper approximation generated by the L-fuzzy relations,the reflexive and symmetric L-fuzzy relations,respectively.

L-fuzzy relations;L-fuzzy rough sets;inner products;axioms

利用L-模糊集内积的概念分别给出了由L-模糊关系、反身、对称的L-模糊关系生成的L-模糊上近似的唯一公理刻画。

L-模糊关系；L-模糊粗集；内积；公理

A

O159.1

10.3778/j.issn.1002-8331.1402-0446

LI Lingqiang.Characterization on L-fuzzy upper approximation by only one axiom.Computer Engineering and Applications,2014,50（24）：1-3.

国家自然科学基金（No.11371130）；山东省自然科学基金（No.ZR2013AQ011）；湖南省科技计划项目（No.2012RS4029）。

李令强（1980—），男，博士后在读，副教授，主要研究领域为格值拓扑与格值粗集。E-mail：lilingqiang0614@126.com

2014-03-04

2014-05-20

1002-8331（2014）24-0001-03

CNKI网络优先出版：2014-08-06，http∶//www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1402-0446.html