一种基于TIN的等值线快速生成算法

赵景昌，白润才，刘光伟，刘 威

1.辽宁工程技术大学 矿业学院，辽宁 阜新 123000

2.辽宁工程技术大学 理学院，辽宁 阜新 123000

一种基于TIN的等值线快速生成算法

赵景昌1，白润才1，刘光伟1，刘 威2

1.辽宁工程技术大学 矿业学院，辽宁 阜新 123000

2.辽宁工程技术大学 理学院，辽宁 阜新 123000

1 引言

在数字矿山建设过程中，应用三维地学模拟（3D Geoscience Modeling，3DGM）技术建立三维矿床地质模型是重要的基础工作之一。以各种勘测方法与手段获得的地质与地形数据，在空间上的分布呈离散形式且数据量有限，利用这些有限的离散空间信息恢复地质属性和地学变量的空间分布状态，研究它们在空间上的分布特征和变化规律，最常用的一种方法就是绘制等值线图。

基于离散数据生成等值线图的方法主要有规则矩形格网（Grid）法和不规则三角网（Triangulated Irregular Network，TIN）法等两种。规则矩形格网法首先要根据已知的离散点数据进行网格化插值，构建矩形网格模型，然后从边界或者内部网格单元出发，根据网格单元各边端点的属性值内插等值点，并连接等值点形成等值线；不规则三角网法则是将已知的离散点按一定规则进行三角剖分构建TIN模型，然后在TIN各三角面片单元中内插等值点生成等值线。格网法对边界拟合能力较差，无法处理等值线断续等现象，并且在利用离散点数据进行网格化插值过程中，必然造成原始数据附近的数据失真，影响等值线分布的准确性；而不规则三角网法可基于原始离散点数据直接生成TIN模型，在保持原有数据精度的情况下，能较为准确地表达复杂地质构造的地层局部特征，且三角形构造灵活，对内外边界拟合较好，因此应用广泛[1]。

基于TIN生成等值线图可分解为两个基本步骤：（1）在TIN中确定含某等值线起点的起始等值边，即：起始等值边查找；（2）从起点出发按某种访问策略在TIN中内插等值点并连接成等值线，即：等值点内插与等值线追踪。随着TIN数据规模的不断增长以及对离散数据分布特征和变化规律进行实时分析的需要，对以上两个步骤的时间效率提出了越来越高的要求，而以往基于TIN生成等值线的研究成果主要集中于有断层情况下等值线的生成[1]、传统等值线生成方法的改进[2-4]、等值线内插[5]以及等值线填充[6-7]等。在上述研究成果中，关于如何提高等值线生成算法时间效率的研究较少，在起始等值边查找、等值点内插计算及等值线追踪时，通常采用遍历策略，算法时间效率较低，很难满足大数据量条件下等值线快速生成的需要。

Marc Van Kreveld在文献[8]中提出了一种区间树索引算法，将起始等值边的查找效率从O(M×N)（M为生成的等值线条数，N为TIN中三角面片数）提高到O(lbN+k)（k为目标区间数目），但由于在构建区间树索引时，需要预先确定各级树节点的最优分割值而导致算法整体效率下降，并且，关于如何提高等值线追踪的时间效率问题，在文献[8]中也未进行深入探讨。

本文在进行数字露天矿软件研发过程中，针对大数据量条件下等值线生成的时间效率问题，设计并实现了一种基于TIN的等值线快速生成算法，实验及应用表明，该算法时间效率高，等值线生成精度可靠，能够满足大数据量条件下等值线快速生成的需要。

2 本文算法思想与数据结构

从三角面片规模为N的TIN中查找一条含有某等值线起点的起始等值边时，最直接的方法就是对TIN中的每个三角面片进行顺序遍历，当生成的等值线规模为M时，查找起始等值边的时间效率为O(M×N)，当等值线所经过的三角面片数很少或者分布零散时，这种遍历算法的时间效率显然太低了，在TIN数据规模比较大的情况下尤为明显。

如果将TIN中的三角面片以所关心的等值线属性值进行升序或降序排列，然后在有序的三角面片集合中用二分查找思想查找含有某给定等值线属性值的三角面片，对等值线生成算法效率的提高无疑是有益的。假设某三角面片的三个顶点分别为 P1(x1，y1，v1)，P2(x2，y2，v2)，P3(x3,y3,v3)，拟生成的某等值线属性值为v，则该三角面片包含等值点的充要条件是：min{v1,v2,v3}≤max{v1,v2,v3}。TIN中每个三角面片三个顶点的属性值所对应的是一个一维区间[min{v1，v2，v3}，max{v1，v2，v3}]（当三个顶点属性值相等时会退化为一个点），相当于将三角面片投影到等值线属性值所对应的坐标轴上，因此，可以将查找含有某等值点的起始等值边问题看作是一维查找问题，即：在某坐标轴上给定一组区间，将包含待查询属性值v的所有区间报告出来。解决这类问题的有效方法之一就是利用区间树索引[6]，然而，在构建区间树时，需要预先确定能够同时顾及区间树深度、平衡程度以及树节点中元素个数的最优分割值，无论采用排序方法还是统计方法都需要耗费大量时间，当TIN数据规模较大时，时间效率较低，难以满足实际应用需要。

本文算法借鉴区域树[9]思想，首先建立一棵以三角面片顶点最小属性值为键值的平衡二叉树（本文选用查找效率较高的红黑树），其中序遍历序列为按顶点最小属性值升序排序的三角面片序列，按三角面片包含等值点的充要条件，将中序遍历序列位于某节点以左的所有三角面片再按顶点最大属性值降序排列，在降序序列中用线性查找方法即可快速确定包含某等值线起点的三角面片以及该三角面片中的起始等值边，用上述算法思想查找起始等值边的时间复杂度为O(lbN)，实验证明，由于不需要预先确定节点的最优分割值，本文红黑树索引算法在起始等值边查找时的整体效率要优于区间树索引算法。

影响等值线生成效率的另一个因素就是等值线追踪。由TIN生成的等值线是由内插计算得到的等值点连接而成的，每个被等值线穿过的三角面片必有两条含有等值点的边，一条为等值线“入边”，另一条为等值线“出边”，如果在内插计算等值点时，能够确定与当前“出边”存在邻接关系的下一个三角面片，则只需顺序记录各三角面片“出边”上的等值点，并按最终得到的顶点序列绘制等值线就完成了等值线的追踪。“出边”与三角面片的邻接关系可根据TIN中“边—面（三角面片）”拓扑确定，本文算法在读取TIN数据时，基于散列与半边数据结构快速重建TIN拓扑，从而使等值线追踪与等值点内插计算同步完成，进一步提高了算法的整体时间效率。

本文算法中的主要数据结构如图1所示。

图1 本文算法主要数据结构

3 TIN拓扑重构

重建TIN拓扑的主要目的是实现等值线的快速追踪。本文中假设TIN是采用某种三角剖分算法预先生成的模型，因此在生成等值线之前需要读入TIN数据，并在读取TIN数据的同时完成TIN拓扑重建。

TIN拓扑包括“顶点—顶点”、“顶点—边”、“边—面（三角面片）”之间的邻接关系，常见的可用来表示这种拓扑关系的数据结构有：四边结构[10]（Quad-edge Structure）、半边结构（Half-edge Structure）[11]、翼边结构（Wing-edge Structure）、放射边结构（Radial-edge Structure）[12]等。其中半边数据结构可以使TIN中三角面片之间的邻接关系更加容易表示，因此本文中选择半边数据结构来描述TIN拓扑关系，共包含：TIN（三角网）、Face（面，TIN中的三角面片）、Edge（边）、Half edge（半边）、Vertex（顶点）等5类节点。TIN中每个三角面片由3条首尾相连的有向半边组成，两个相邻的三角面片一定存在一对重合的、方向相反的半边，称之为伙伴半边，两个伙伴半边构成一条整边，如图2所示。

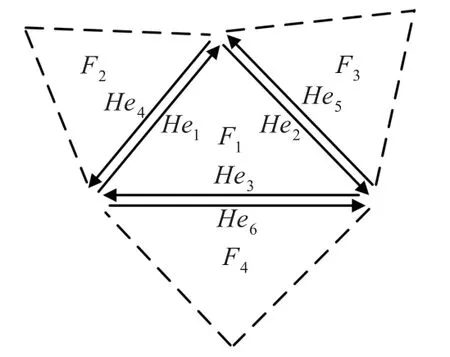
图2 TIN半边数据结构示意图

顶点聚合与半边合并是建立TIN拓扑表示的关键，而顶点聚合又是半边合并的基础，其任务是将在TIN各三角面片中重复出现的顶点表示为唯一顶点。顶点聚合算法大致可分为直接法、平衡二叉树法和散列法等三类，其中直接法的时间复杂度为O(N2)（N为TIN顶点个数），平衡二叉树方法的时间复杂度为O(N lbN)，而基于散列的方法在理想情况下的时间复杂度为O(N)。

本文采用散列法进行顶点聚合，计算散列地址的散列函数为：

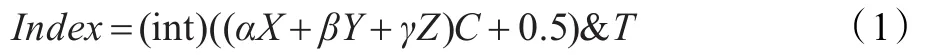
其中X，Y，Z为顶点坐标；α，β，γ为顶点坐标系数，Jan[13]等通过大量实验研究认为α=3，β=5，γ=7较合理；C为比例系数，一般尽量使计算机所能表达的整型数的字长范围都被利用，T为散列表的长度，一般是计算机所能表达的整型数的范围，其值在(0，2k)之间。

采用散列函数计算顶点散列地址时，两个不同顶点的散列地址可能会发生“冲突”，本文采用链地址法处理“冲突”，即：将发生地址冲突的顶点存储在散列表同一个槽内的线性链表中。

半边合并的任务是将两个端点完全相同的半边设置成伙伴半边，从而建立起“边—边”、“边—面（三角面片）”之间的邻接关系。在顶点聚合的同时，可通过为每个顶点建立一个入射半边索引表[14]进行半边合并。

基于散列与半边数据结构的顶点聚合及半边合并步骤如下：

（1）读入一个新三角面片Fi。

（2）应用式（1）所示散列函数计算Fi三个顶点V1，V2，V3散列地址，若散列表中此地址槽链表非空，判断当前顶点与该地址槽内的其他顶点是否重合，若不重合，为此顶点设置ID为num+1（num非重复顶点数），并将其插入到该地址槽内的顶点链表中，若重合，则将此顶点ID设置为与其重合的顶点ID。

（3）如图3所示，Fi中半边He1的两个顶点V1，V2均存在重合顶点，则对半边He1进行合并（即找出与He1端点相同但方向相反的半边—伙伴半边）。

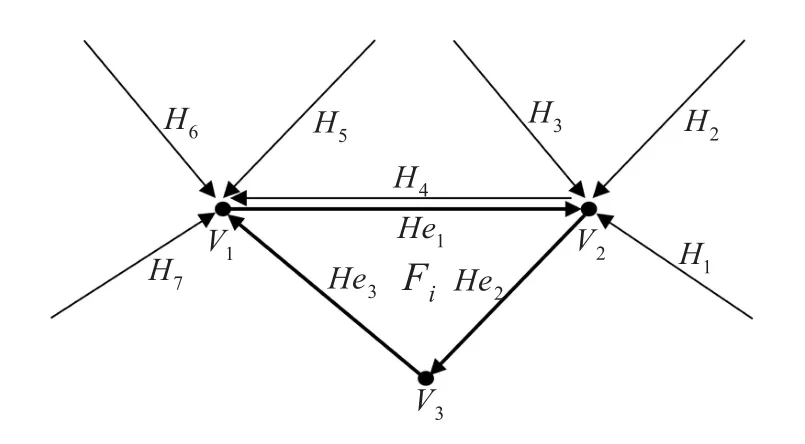
图3 TIN半边合并示意图

（4）He1以V1为起点，它的伙伴半边一定以V1为终点，故只需在V1的入射半边表中，根据半边端点ID是否相等查找He1的伙伴半边即可，在图3中，V1的入射半边表包括半边H4，H5，H6，H7，其中H4与He1的端点重合且方向相反，因此H4为He1的伙伴半边。

（5）更新相应顶点的入射半边表。以图3为例，将He1从V1的入射半边表中删除（不会再出现He1的伙伴半边），同时需要给V1增加一个新的入射半边He3，对新顶点V3建立入射半边表，并将He2作为V3入射半边插入到表中。

（6）将Fi中的半边He1，He2，He3加入到TIN半边集合中。

（7）重复执行步骤（1）～（6），直至TIN中所有三角面片均被读入为止。

顶点聚合与半边合并时，将半边加入到各顶点的邻接半边集合，将三角面片加入到各半边的邻接三角面片集合，即完成了对TIN的拓扑重构。

4 等值线生成

4.1 构建以TIN三角面片为节点的红黑树

为快速查找待插等值线的起始等值边，需要构建以TIN三角面片为节点的红黑树。

红黑树[15]是由Rudolf Bayer在1972年设计出来的一种每个节点都具有颜色特性的自平衡二叉搜索树，通过对树中节点适当染色，可以使树处于近乎完美的平衡状态。除了具有一般二叉搜索树的特征外，红黑树必须遵循如下规则：（1）树中的每个节点或为红色，或为黑色；（2）根节点永远为黑色；（3）所有叶子节点都是空节点，且为黑色；（4）若某节点为红色，则其子节点必须是黑色；（5）从某一节点到其子孙叶子节点的每条简单路径上都必须包含相同数目的黑色节点。

遵循上述规则构建的含有N个内部节点的红黑树，其高度至多为2lb(N+1)，所以上述约束条件强制规定了红黑树的关键属性，即：从根节点到叶子节点最长可能路径不超过最短可能路径的两倍，因此，红黑树可保证在最坏情况下在O(lbN)时间内完成动态集合操作（如查找、插入和删除），是一种查找效率非常高的自平衡二叉树。

设TIN中某三角面片三个顶点属性值分别为v1，v2，v3，待插等值点属性值为v，则该三角面片中包含待插等值点的充要条件为：min{v1，v2，v3}≤v且max{v1，v2，v3}≥v。

基于以上特性，本文以TIN中的三角面片为节点，以三角面片三个顶点的最小属性值为键值构建红黑树，当新节点插入红黑树时，必须满足红黑树的建树条件，节点颜色属性可以遵循红黑树的5点规则设定，同时为了使新节点插入后仍满足建立二叉搜索树所必须的条件，定义节点比较规则为：

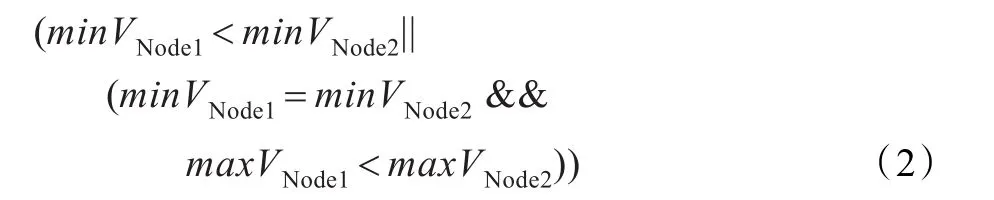
其中VNode1，VNode2为三角面片节点属性值。满足以上条件时，节点Node1＜Node2，当新插入节点与某节点最小与最大属性值均相等时，将新节点插入到该节点的左子树中。

关于红黑树的具体实现，在文献[16]中有详细介绍，在此不作赘述。

4.2 起始等值边查找

红黑树创建后，需要先对红黑树进行一次中序遍历，并将各节点在中序遍历序列中的顺序ID存入到节点中，以提高后续查找操作的效率。

在红黑树中查找某待插等值线起始等值边的步骤如下：

（1）以红黑树根节点为当前节点current=root，判断当前节点最小属性值minV与待插等值线属性值V的关系。

（2）若 current.minV＜V，查找当前节点右子树current=current.right，直到current.minV＞V（或叶子节点），若当前节点非叶子节点时，转而查找当前节点左子树current=current.left，直到current.minV＞V（或叶子节点）。

（3）若 current.minV＞V，查找当前节点左子树current=current.left，直到current.minV＜V（或叶子节点）时，若当前节点非叶子节点时，转而查找当前节点右子树current=current.right，直到current.minV＜V（或叶子节点）。

（4）在红黑树中序遍历序列中，取当前节点中序遍历顺序ID以左的所有节点（即中序遍历顺序ID小于当前节点中序遍历ID），按节点最大属性值降序排序。

（5）以顺序查找方式在节点最大属性值降序序列中，查找最大属性值小于待插等值线属性值的节点，则该节点以左的所有节点即构成包含待插等值点的候选三角面片集合。

4.3 等值点计算

完成包含待插等值点的三角面片查找后，即可在候选三角面片集合中以半边为单位进行等值点内插计算。设三角面片按逆时针方向排列的三个顶点分别为P1(x1，y1，z1)，P2(x2，y2，z2)，P3(x3，y3，z3)，以顶点命名的三条半边分别为P1P2，P2P3，P3P1，每条半边顶点最大属性值为maxV，最小属性值为minV，当前追踪的等值线的属性值为v，在判断三角面片中某条边是否含有等值点时，包括以下三种情况：

（1）(maxV-v)(minV-v)＞0，则该半边不含等值点；

（2）(maxV-v)(minV-v)＜0，则该半边含等值点；

（3）(maxV-v)(minV-v)=0，分为以下三种情况分别处理：

①maxV=v，此时将maxV进行正扰动，即给maxV所对应的顶点属性值加上一个较小的正小数ε（本文中ε=10-6）。

②minV=v，此时将minV进行负扰动，即在minV所对应的顶点属性值减去一个较小的正小数ε（本文中ε=10-6）。

③maxV=minV=v，该边不含等值点。

位于某条半边上的等值点的坐标可用线性内插公式求出：

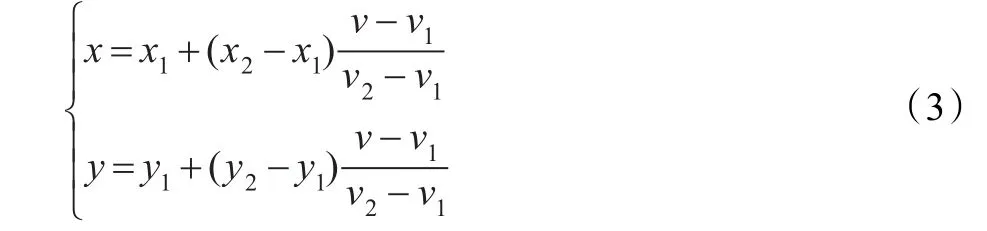
4.4 等值线追踪

为了叙述方便，将TIN中的半边和三角面片按以下方式命名：TIN中不存在伙伴半边的半边为“边界半边”，存在伙伴半边的半边为“内部半边”；TIN中含有“边界半边”的三角面片为“边界三角面片”，不含“边界半边”的三角面片为“内部三角面片”。

等值线追踪的任务就是在含有等值点的候选三角面片集合中以正确的顺序获取属于同一条等值线的等值点并将其连接成为等值线。等值线包括闭合等值线与非闭合等值线两种，其中非闭合等值线的起点位于TIN“边界三角面片”上，而闭合等值线的起点则位于“内部三角面片”上。

基于本文第3章所建立的TIN拓扑结构，在候选三角面片集合中追踪某给定属性值的非闭合等值线可在等值点内插计算的同时按以下步骤进行：

（1）从候选三角面片集合中选取一个“边界三角面片”。

（2）以该三角面片中含等值点的“边界半边”为等值线在该三角面片中追踪的“入边”，计算等值点位置并将其加入当前追踪等值线的顶点集合中。

（3）在三角面片中确定等值线的“出边”，计算等值点并将其加入当前追踪等值线的顶点集合中，同时将该三角面片从候选三角面片集合中删除。

（4）根据TIN中“边—边”、“边—面”拓扑关系，确定当前三角面片等值线“出边”的伙伴半边及其所在三角面片。

（5）在其伙伴半边所在的三角面片中，伙伴半边即为等值线追踪“入边”，该边不需再计算等值点，只需确定等值线在该三角面片中的“出边”，计算出边等值点并将其加入到当前追踪等值线的顶点集合中。

（6）若当前含等值点的半边无伙伴半边（即该边是TIN的“边界半边”），则当前等值线追踪结束，根据等值线顶点集合中的坐标绘制等值线，否则，重复步骤（4），（5），直到当前等值边为TIN“边界半边”为止。

闭合等值线的追踪步骤与非闭合等值线类似，所不同的是闭合等值线的起始半边是“内部半边”，并且等值线追踪结束的条件为当前等值边与该等值线起始等值边为伙伴半边。当候选三角面片集合为空时，当前给定属性值的所有等值线追踪完毕。

5 实验分析与应用实例

5.1 实验分析

本文算法基于Visual Studio.NET平台用C#语言实现，并与无索引算法以及文献[8]中提出的区间树索引算法进行了对比分析。测试平台：Windows 7中文旗舰版，Intel®CoreTMi7-2720QM CPU 2.20 GHz，4 GB内存。

表1为不同数据规模条件下三种算法在预处理阶段、等值线生成阶段的效率对比（表中所列预处理时间包括TIN拓扑重构以及红黑树或区间树构建时间）。

从表1实验结果可知，本文与文献[8]算法分别建立TIN红黑树索引与区间树索引来提高起始等值边的查找效率，尽管在预处理阶段需要耗费一定的时间，但等值线生成的整体时间效率均显著优于无索引算法。在理论上，本文提出的红黑树索引算法与文献[8]提出的区间树索引算法其构建与查找效率均为O(lbN)（N为TIN中三角面片数），但文献[8]算法在构建区间树时，需要预先确定同时顾及区间树深度、平衡程度以及树节点中元素个数的节点最优分割值，无论采用排序方法还是统计方法都需要耗费大量时间，而本文算法在构建以TIN三角面片单元为节点的红黑树过程中，是通过节点旋转和颜色调整来动态保持树的平衡状态，不需要预先确定节点最优分割值，因此，本文算法在预处理阶段的实际时间效率要明显优于文献[8]算法；此外，本文算法基于散列与半边数据结构重构TIN拓扑，在等值点内插计算的同时，根据“边—面”拓扑关系同步完成等值线追踪，从而使本文算法在等值线生成阶段的时间效率也较文献[8]算法有较大提高。

表1 本文算法与区间树及无索引算法效率比较

5.2 应用实例

本文算法已应用在笔者开发的露天煤矿采剥计划CAD软件系统中，图4与图5分别为应用本文算法基于某矿煤层底板TIN与地形TIN生成的煤层底板等值线与地形等高线图。

图4 某矿煤层底板TIN与底板等值线

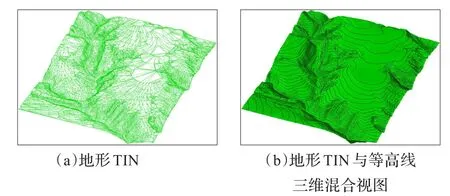
图5 某矿地形TIN与地形等高线

实际应用证明，本文算法运行稳定，生成的等值线精度可靠，能够满足较大数据量条件下基于各种离散的地质、地形数据快速生成等值线的需要。

6 结束语

基于TIN生成等值线能够在保持原有数据精度的情况下，较为精细地表达含复杂地质构造的地层局部特征，且三角形构造灵活，对内外边界拟合较好，因此使用最广泛。起始等值边查找与等值线追踪是决定等值线生成效率的两个关键因素，本文算法通过构建以TIN三角面片单元为节点的红黑树进行起始等值边的快速查找，并基于散列与半边数据结构重建TIN拓扑，在等值点内插计算的同时，根据TIN中“边—面”拓扑关系完成等值线追踪。实验及实际应用表明，本文算法时间效率高，运行稳定，生成的等值线精度可靠，能够满足大数据量条件下等值线快速生成的需要，具有广泛的实际应用价值。

[1]陈学工，付金华，马金金，等.约束TIN生成带断层等值线图的方法[J].计算机工程与应用，2011，47（33）：198-201.

[2]李利军，袁尤军，王乘.一种基于不规则三角网TIN的等值线计算方法[J].计算机与数字工程，2007，35（9）：34-36.

[3]胡金虎.基于不规则三角网的高精度等值线生成方法[J].工程勘察，2011（2）：64-68.

[4]张梅华，梁文康.一个三角形网格上等值线图的绘制算法[J].计算机辅助设计与图形学学报，1997，9（3）：213-217.

[5]徐道柱，刘海砚.一种基于约束边Delaunay三角网的等高线内插方法[C]//第十二届全国图象图形学学术会议论文集.北京：清华大学出版社，2005：505-508.

[6]汤子东，郑明玺，王思群，等.一种基于三角网的等值线自动填充算法[J].中国图象图形学报，2009，14（12）：2577-2581.

[7]李强，李超，甘建红.基于三角网的等值线填充算法研究[J].计算机工程与应用，2013，49（5）：185-189.

[8]van Kreveld M.Efficient methods for isoline extraction from a TIN[J].International Journal of Geographical Information Systems，1996，10（5）：523-540.

[9]Berg M，Cheong O，Kreveld M V，等.计算几何——算法与应用[M].邓俊辉，译.北京：清华大学出版社，2009：136-141.

[10]O’Rourke J.Computational geometry in C[M].2nd ed. Cambridge：Cambridge University Press，1998：146-149.

[11]Mantyla M.An introduction to solid modeling[M].[S.l.]：Computer Science Press，1988：110-132.

[12]Weiler K.Edge-based data structures for solid modeling in curved-surface environments[J].IEEE Computer Graphics and Applications，1985，5（1）：21-40.

[13]Skala V，Hrádek J，Kuchař M.Hash function for triangular mesh reconstruction[C]//WSEAS International Conference：Recent Advances in Computer Engineering，WSEAS，2009：233-238.

[14]刘金义，侯宝明.STL格式实体的快速拓扑重建[J].工程图学学报，2003（4）：34-39.

[15]左飞.C++数据结构原理与经典问题求解[M].北京：电子工业出版社，2008：418-433.

[16]Michael M.Data structures and algorithms using C#[M]. Cambridge：Cambridge University Press，2007：270-275.

ZHAO Jingchang1,BAI Runcai1,LIU Guangwei1,LIU Wei2

1.School of Mining,Liaoning Technical University,Fuxin,Liaoning 123000,China
2.College of Science,Liaoning Technical University,Fuxin,Liaoning 123000,China

Generating isogram based on TIN is one of the important means to recover the geological properties and variables distribution with the finite discrete spatial information.Its time efficiency mainly depends on the initial edge with isoline point checking and isolines tracking.By building the red-black tree with triangular facets units as TIN node,the time complexity of the initial edge checking is improved fromO(M×N)toO(lbN);TIN topology is reconstructed based on hash and half-edge data structure.According to“side-face”topology,isolines tracking is synchronously completed with the isoline points interpolation.Experiments and practical application show that the algorithm is stable,the precision of the isolines generation is reliable,and the algorithm can meet the needs to quickly generate isolines with the large amount of data,and has a wide range of practical application value.

Triangulated Irregular Network（TIN）;isoline;red-black tree;hash;half-edge data structure;topology reconstruction

基于TIN生成等值线图是利用有限的离散空间信息恢复地质属性和地学变量空间分布状态的重要手段之一，其时间效率主要取决于起始等值边查找与等值线追踪。通过构建以TIN三角面片单元为节点的红黑树，将起始等值边查找的时间复杂度由O(M×N)提高到O(lbN)；基于散列与半边数据结构重建TIN拓扑，根据TIN中“边—面”拓扑关系，在等值点内插计算的同时完成等值线追踪。实验及应用表明，算法时间效率高，生成的等值线精度可靠，可满足大数据量条件下等值线快速生成的需要，具有广泛的实际应用价值。

不规则三角网（TIN）；等值线；红黑树；散列；半边数据结构；拓扑重构

A

TP391.7

10.3778/j.issn.1002-8331.1404-0482

ZHAO Jingchang,BAI Runcai,LIU Guangwei,et al.Fast isolines generation algorithm based on TIN.Computer Engineering and Applications,2014,50（24）：10-15.

国家自然科学基金（No.51174106）；辽宁省教育厅科学研究一般项目（No.L2011051）。

赵景昌（1974—），男，博士研究生，讲师，研究领域为数字露天矿，露天开采理论与技术；白润才（1961—），男，博士，教授，研究领域为数字矿山，露天开采理论与技术，露天矿边坡稳定与控制；刘光伟（1981—），男，博士，讲师，研究领域为数字矿山，露天开采理论与技术；刘威（1977—），男，博士研究生，副教授，研究领域为数字露天矿，矿业系统工程，数据挖掘理论及应用。E-mail：lntuzjc@126.com

2014-05-05

2014-07-04

1002-8331（2014）24-0010-06

CNKI网络优先出版：2014-08-19，http∶//www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1404-0482.html