基于双目视觉的无人飞行器目标跟踪与定位

张 梁，徐锦法

南京航空航天大学 直升机旋翼动力学国家级重点实验室，南京 210016

基于双目视觉的无人飞行器目标跟踪与定位

张 梁，徐锦法

南京航空航天大学 直升机旋翼动力学国家级重点实验室，南京 210016

1 引言

近年来国内外在摄像机目标跟踪领域展开广泛研究。基于色彩空间的目标识别与跟踪[1-4]针对光照相对恒定的室内环境以及背景色彩相对单一的室外环境比较有利。Teuliere[5]等人使用四旋翼飞行器，搭载下视的单目摄像机，跟踪实验室内的红色模型赛车，通过IMU得到飞行器高度，实现了目标跟踪与定位以及航向角锁定。Miguel[6]等人同样使用四旋翼飞行器，搭载前视的单目摄像机，跟踪红色的气球，通过计算特征面积得到相对距离，使用模糊控制实现了目标定位跟踪。

Camshift[7]算法是基于颜色的特征跟踪算法，是Meanshift[8]（均值偏移）算法的扩展算法，将Meanshift算法扩展到了实时连续图像跟踪，且跟踪窗口可根据目标实时缩放，因此具有较好的跟踪与定位效果，目前应用相对广泛。

使用单目摄像机进行目标定位需借助辅助传感器进行测距，或者目标大小信息已知，因此受限较多。采用双目摄像机可避免增加其他方式传感器，处理方式简便，且无需预知目标尺寸等信息，适用范围更广[9-11]。

基于以上特点，本文提出了一种基于Camshift算法的目标跟踪方法，通过在六旋翼无人飞行器上搭载双目视觉系统（如图1所示）实现对目标的测距与定位，采用卡尔曼滤波算法减小噪声干扰，使测距与定位更稳定。

图1 六旋翼实验平台

2 Camshift目标跟踪算法

Camshift（Continuously Adaptive Mean-Shift）算法是连续自适应Meanshift算法的简称，以Meanshift算法为核心，实现图像任一时刻的Meanshift迭代计算，再以此刻得到的目标窗口为下一时刻Meanshift算法搜索窗口初始值。进行Meanshift算法计算前，首先需要得到颜色概率分布图，将目标从原图像中分离出来。

2.1 反向投影

得到颜色概率分布图是进行Meanshift算法计算的前提，由此可从背景中提取出跟踪物体。通过对图像进行反向投影[12]（Back Projection）得到颜色概率分布，即反向投影图。反向投影反映了原图像中某像素点与目标色彩直方图模型的对应关系，直方图反映了颜色的概率分布，因此反向投影可得到目标色彩在原图像中的概率分布情况。

反向投影过程如下：

（1）对原图像进行颜色空间转换，转换至HSV（色度、饱和度、亮度）空间，并提取出H分量。HSV空间可消除亮度对色彩提取的干扰。

（2）选取目标区域，对目标区域像素点H分量进行统计，得到色彩直方图，并量化至0～255。

（3）选取原图像中某一像素点，将H分量与目标色彩直方图进行匹配，并将匹配所得直方图中的数值作为反向投影图中该像素点对应坐标下像素点的像素值。

（4）重复步骤（3），直至原图像中所有像素点均经过匹配，由此得到反映目标颜色概率分布的反向投影图。

反向投影结果图2所示，选取绿色圆形图案作为跟踪目标，对其进行反向投影，结果如图2右图所示，目标被很好地从背景中分离出来。

图2 目标反向投影结果

2.2 Meanshift算法

Meanshift算法是均值偏移算法，是跟踪应用领域中寻找数据密度分布局部极值的一种迭代方法。

Meanshift算法迭代收敛过程如图3所示，其步骤可归纳为：

（1）选择搜索窗口初始位置；

（2）计算窗口中像素点重心；

（3）将窗口中心移至重心处；

（4）重复（2）、（3）步骤直到算法收敛。

图3 Meanshift算法迭代收敛过程

窗口中像素点重心可表示如下：

经过Meanshift迭代收敛的窗口中心即为跟踪目标的中心，便可对目标进行定位跟踪。

2.3 Camshift算法

Camshift算法的自适应性主要体现在其跟踪窗口大小可根据目标变化而自动调整。Camshift算法具体步骤如下：

（1）选取待跟踪目标区域，并计算此区域色彩直方图，同时设定初始搜索区域。

（2）读取当前时刻原始图像，经过反向投影得到反向投影图，从背景中分离出跟踪目标。

（3）使用Meanshift算法收敛搜索区域。

（4）将收敛区域集中，调整跟踪窗口大小。

（5）重复（2）～（4）步骤。

当目标尺度发生变化时，Camshift算法可通过步骤（4）将收敛区域集中，用以调整跟踪窗口大小，以便进行自适应跟踪。

3 双目相机特征点三维重建

使用双目摄像机优势在于能够提供对象的深度信息，实现像素点三维坐标重建。本文所用双目相机已进行了相机标定，标定方法参见文献[13]，所获得的图像也已进行了立体校正，标定与校正方式参见文献[12]。经过Bouguet方法校正后两摄像机光轴平行并相交于无穷远，同时两图像实现行对准，立体校正为图像重新选择图像中心与边界，使两图像叠加视图面积最大化，校正后两摄像机具有相同主点与焦距，即具有相同的内参。

摄像机模型坐标系对应关系如图4所示，为方便图像平面与摄像机模型坐标转换，将摄像机坐标系坐标轴取为：X轴与图像坐标系u轴平行，Y轴与图像坐标系v轴平行，Z轴与光心重合。根据透视投影关系，基本针孔摄像机模型的空间任意一点P与图像平面对应关系可表示为：

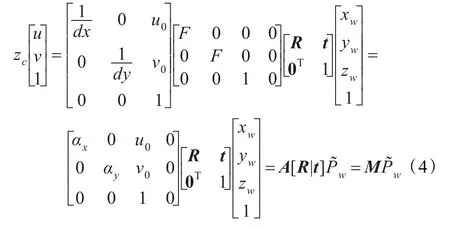
式中zc是摄像机坐标系下Z轴坐标；u、v是图像坐标系下像素坐标值；dx、dy是图像坐标系下每一个像素在x轴和y轴方向的物理尺寸，单位为mm；u0、v0是摄像机光轴与图像平面的交点坐标值；F是相机焦距；R、t分别是世界坐标系相对于摄像机坐标系的旋转矩阵和平移向量；xw、yw、zw分别是该特征点在世界坐标系下坐标值；αx=F/dx、αy=F/dy；M 称为投影矩阵，而A和[R|t]分别称为摄像机的内参和外参，上标～表示齐次向量。

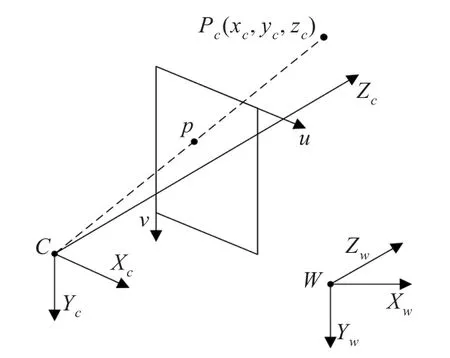
图4 各坐标系间关系

特征点三维重建时所用相机参考坐标系为左相机坐标系，即所求得的特征点三维信息是在左相机坐标系下求得的。根据双目相机三角测量法[14]，如图5所示，假定两摄像机内参相同，且两坐标系仅在x轴相差一段距离B，即基线距离，公共视场空间点P(xc，yc，zc)在左右摄像机坐标系下坐标分别为P(xc，yc，zc)和P(xc-B，yc，zc)，两图像平面对应特征点为 pL(uL，vL)、pR(uR，vR)，图像已校正，即vL=vR。

图5 双目视觉图像重建示意图

由图5可知，根据相似三角形定理以及摄像机投影方程公式（4），存在如下关系：

由左、右像平面的 pL和 pR坐标计算得到空间点P在摄像机坐标系内三维坐标值，实现了特征点三维重建。

4 目标跟踪与定位

Camshift算法可确定目标中心在图像平面中所处位置，对左右相机同一时刻图像分别运行Camshift算法以确定目标的左、右中心，通过双目三角测量法确定目标在左相机坐标系三维坐标。考虑到旋翼飞行器体积不大，假定左相机坐标系与飞行器机体坐标系重合，算法流程图如图6所示。

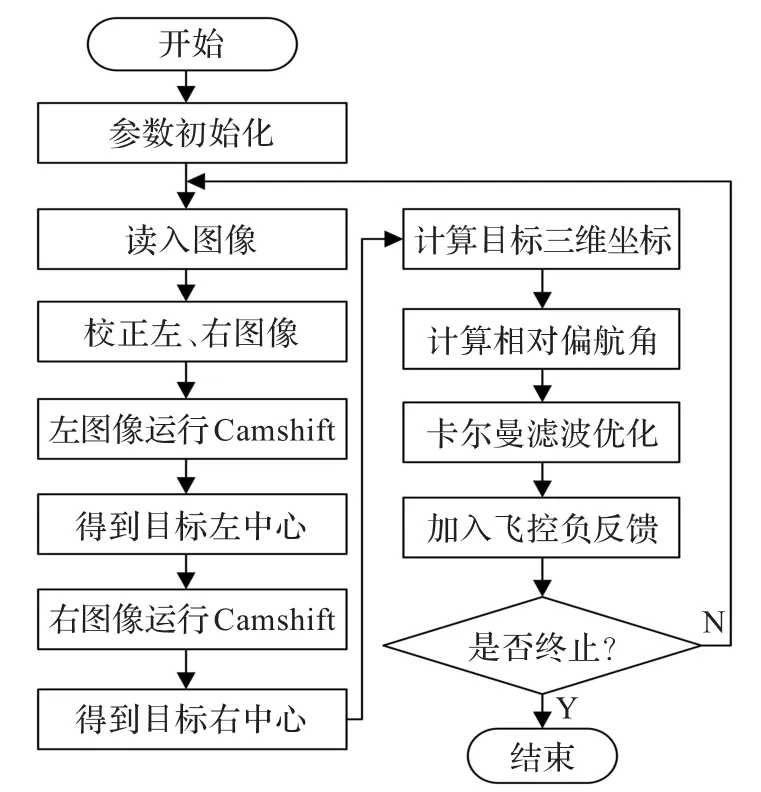
图6 目标跟踪定位算法流程

根据三角测量法可知，目标在机体坐标系三维坐标可用式（6）表示：

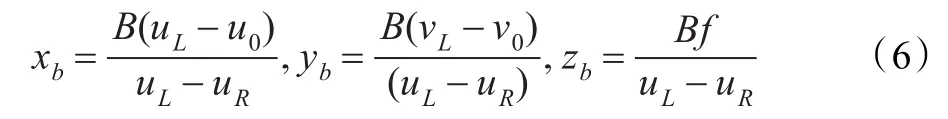
式中，认为相机αx与αy相等，f为相机焦距，单位为像素。

由图4可知，通过相机光轴与目标像素点的偏移可计算相机光心与目标夹角，由此可计算得到相机与目标间的相对偏航角与俯仰角。

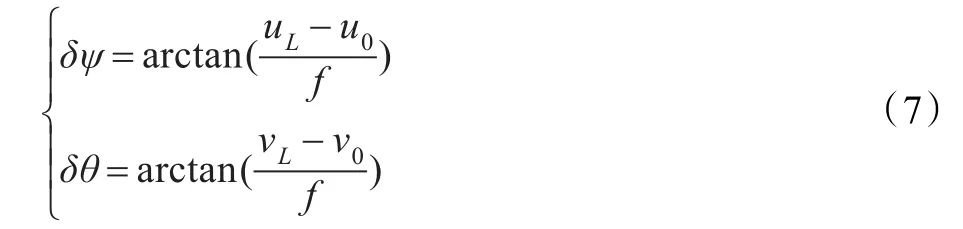
利用求得的飞行器与目标间的相对偏航角δψ可校正飞行器的偏航角，使其正视目标飞行。机体坐标系下深度信息表征飞行器与目标间的相对距离，利用高度与相对偏航角可控制目标处于飞行器视场内。

实际传感器测量存在噪声干扰等影响，应用卡尔曼滤波进行数据滤波估计，能减少噪声干扰，提高数据的稳定性和测量精度。所用的线性卡尔曼滤波状态方程和观测方程为：

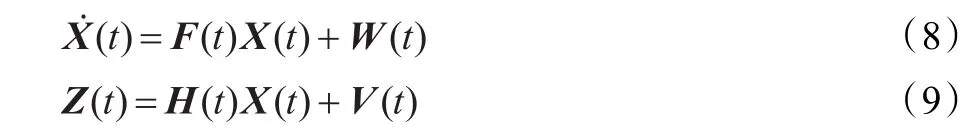
式中，状态矢量为 X=[xbybzbδψ]T，输出矢量为Z=[xbybzbδψ]T，状态矩阵F及量测矩阵H均为4维单位矩阵I。状态误差矢量W和量测误差矢量V均为高斯白噪声。

将图像处理得到的目标三维信息作为飞行轨迹控制的负反馈输入信号，可保证飞行器的航向与距离的稳定与控制，实现飞行器自主跟踪目标。调节控制器参数能改善飞行器的操纵响应，控制结构框图如图7所示，飞行控制系统及控制算法参见文献[15]，本文不再赘述。

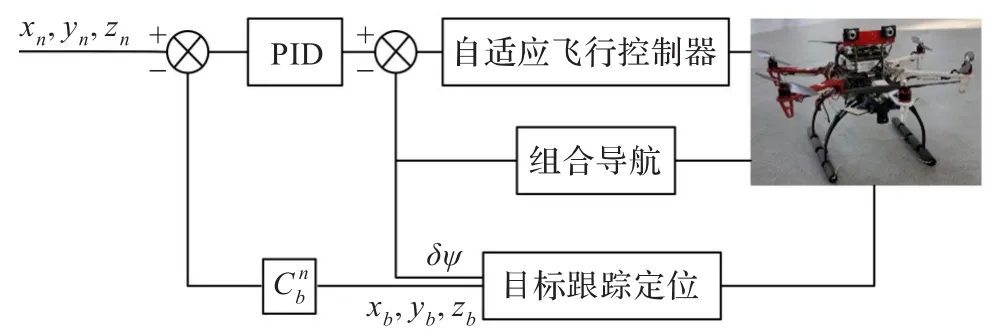
图7 无人机自主飞行跟踪目标控制框图

5 测试结果

为验证所提出算法，应用两台低成本USB相机作为图像采集设备，相机镜头焦距8 mm，两相机间基线长度10 cm，图像尺寸352×288。使用一台笔记本电脑作为图像处理计算机，CPU为Intel T7500，主频达到2.2 GHz，内存为2 GB。运用OpenCV 2.4.7代码库，结合VS2010 C++实现程序编写，Debug模式下帧频达到8 frame/s。六旋翼平台采用MH550，飞控系统为自主研发的自适应飞控系统。

如图8所示为双目视觉目标跟踪地面实验结果，方框区域为目标区域，红点为目标左、右中心。图9所示为一次跟踪任务的三维显示结果，显示了目标在飞行器坐标系下经卡尔曼滤波得到的三维位置估计。图10所示为此次跟踪的相对偏航角变化。图示结果表明目标运动轨迹清晰、三维位置估计值精确。

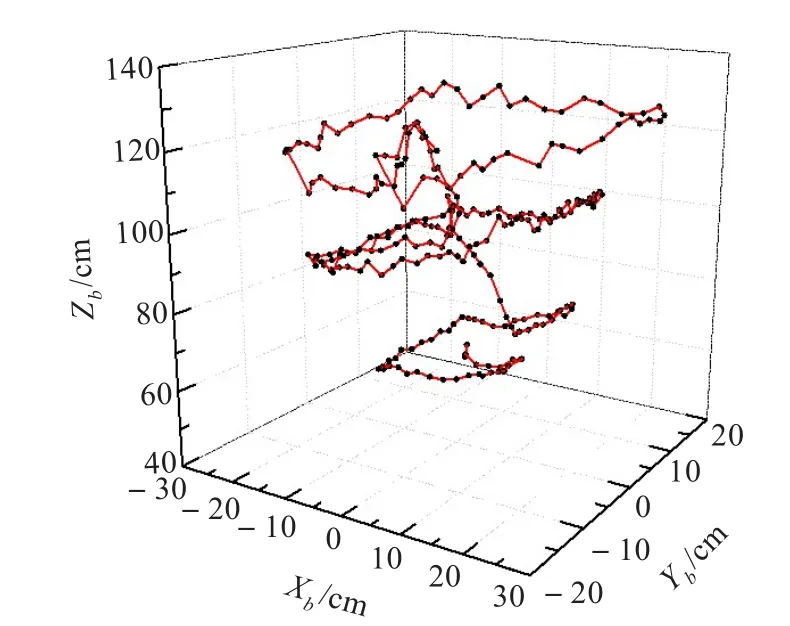
图9 经卡尔曼滤波的地面跟踪结果三维显示

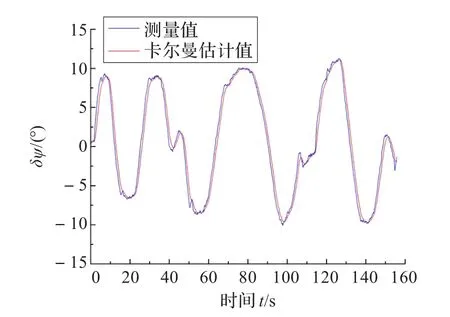
图10 跟踪过程中相对偏航角变化

图11所示为一距离测量结果，米尺测量数据与相机测量结果有2 cm误差，即3.3%误差，从曲线可以看出，经过卡尔曼滤波后，数据更加平滑稳定，减少了随机噪声对测量的影响，卡尔曼滤波计算中系统噪声协方差矩阵与测量噪声协方差矩阵为Q=0.15×I4×4，R= 1×I4×4。

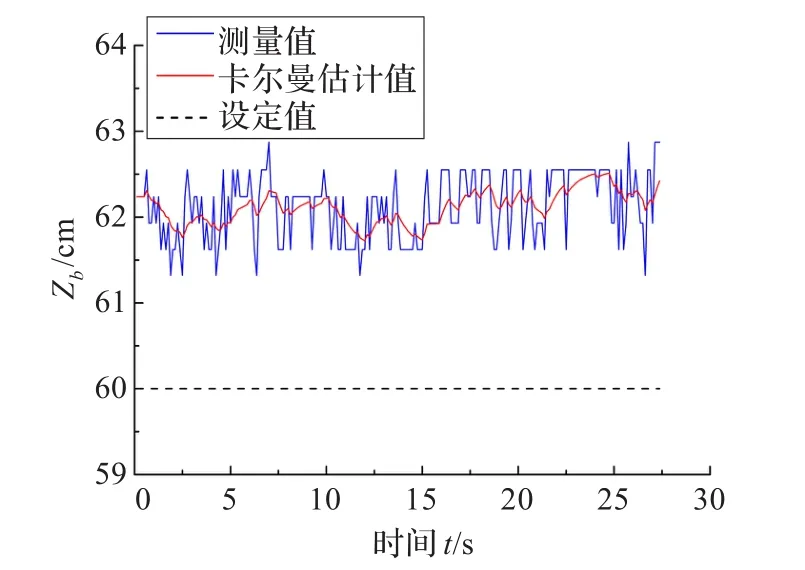
图11 测量过程稳态误差

图12所示为相机移动情况下相机距离正前方目标之间的距离实测结果。图中可见，相机测距跟踪迅速，误差控制在2 cm范围内，经卡尔曼滤波距离估计值能满足飞行器目标跟踪及定位任务要求。

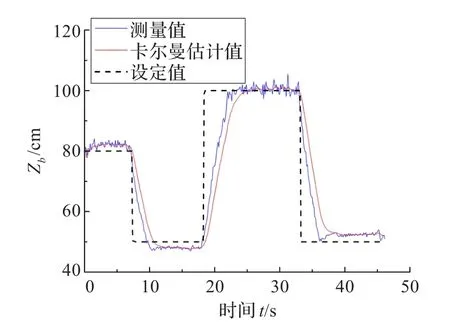
图12 距离测试实验

如图13所示为飞行器目标跟踪测试情况，实现了六旋翼飞行器视觉跟踪定位。实验时相机正视跟踪目标，即相对偏航角为0°，飞行器距离目标2 m，距离地面1 m，机载前向与地向激光测距仪，测量Zb轴目标相对飞行器距离以及飞行器飞行高度（Yb轴），由于目标离地高度已知，地向激光测量值与已知目标离地高度之差即为Yb轴目标相对飞行器距离，并将Zb轴与Yb轴目标相对飞行器的距离作为真值。真值与视觉估计值的差值即视觉估计误差，Zb轴位置误差如图14所示，最大误差±5 cm，Yb轴位置误差如图15所示，最大误差±3 cm。实验表明本文算法稳定可靠，估计误差较小。

图13 无人机视觉跟踪测试

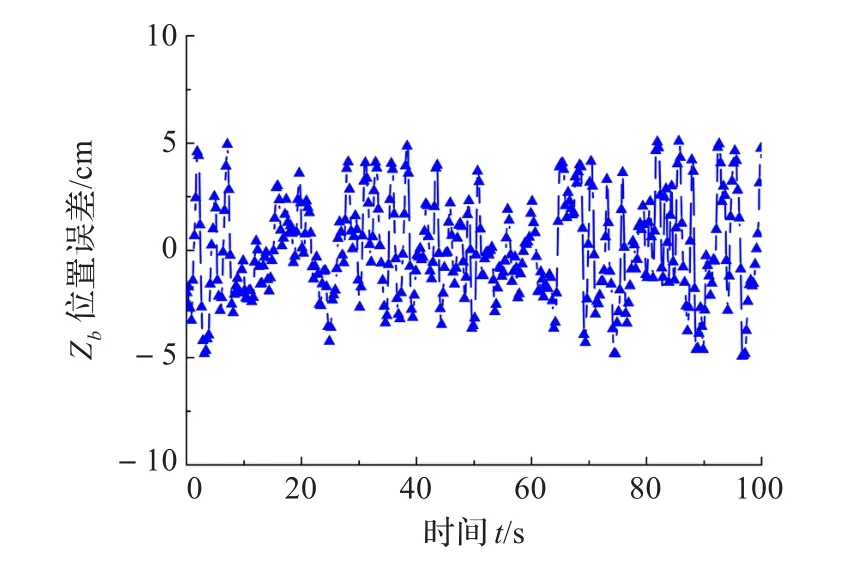
图14 目标跟踪Zb轴位置误差

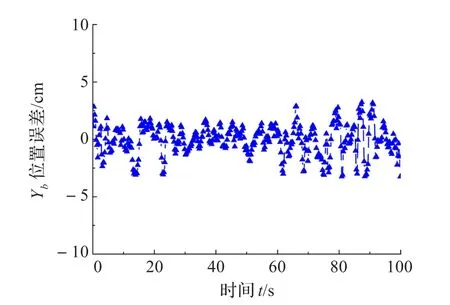
图15 目标跟踪Yb轴位置误差

6 结束语

（1）Camshift算法计算稳定性好，可实现对不同尺寸目标的跟踪，能有效扩大跟踪范围。

（2）基于双目视觉的目标定位估计相比于红外、超声波等测距方式，具有较高的性价比，且可避免反射波被吸收使测量失败等问题。

（3）双目视觉目标跟踪定位结合卡尔曼滤波能有效减小噪声干扰，提高测量精度，可在双目视觉有效距离内将精度控制在±5 cm以内。

（4）地面和飞行跟踪实验结果表明，本文所提出的目标跟踪定位算法稳定可靠，精度较高。

[1]Mohammed A D，Morris T.A robust visual object tracking approach on a mobile device[M]//Information and Communication Technology.Berlin Heidelberg：Springer，2014：190-198.

[2]Hsia C，Liou Y，Chiang J.Directional prediction CamShift algorithm based on adaptive search pattern for moving object tracking[J].Journal of Real-Time Image Processing，2013.

[3]Zin N A M，Abdullah S N H S，Abdullah A.Improved CAMshift based on supervised learning[M]//Robot Intelligence Technology and Applications 2012.Berlin Heidelberg：Springer，2013：611-621.

[4]Hidayatullah P，Konik H.CAMSHIFT improvement on multi-hue object and multi-object tracking[C]//2011 3rd European Workshop on Visual Information Processing（EUVIP），2011：143-148.

[5]Teuliere C，Eck L，Marchand E.Chasing a moving target from a flying UAV[C]//2011 IEEE/RSJ International Conference on Intelligent Robots and Systems（IROS），2011：4929-4934.

[6]Olivares-Mendez M A，Mondragon I，Campoy Cervera P，et al.Aerial object following using visual fuzzy servoing[C]// Proceedings of the 1st Workshop on Research，Development and Education on Unmanned Aerial Systems（RED-UAS 2011），2011：61-70.

[7]Bradski G R.Computer vision face tracking for use in a perceptual user interface[J].Intel Technology Journal，1998.

[8]Comaniciu D，Meer P.Mean shift：a robust approach toward feature space analysis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24（5）：603-619.

[9]Stefanik K V，Gassaway J C，Kochersberger K，et al.UAV-based stereo vision for rapid aerial terrain mapping[J]. GIScience&Remote Sensing，2011，48（1）：24-49.

[10]Shabayek A E R，Demonceaux C，Morel O，et al.Vision based uav attitude estimation：progress and insights[J]. Journal of Intelligent&Robotic Systems，2012，65（1）：295-308.

[11]Kitt B，Geiger A，Lategahn H.Visual odometry based on stereo image sequences with ransac-based outlier rejection scheme[C]//Intelligent Vehicles Symposium（IV），2010：486-492.

[12]Bradski G，Kaehler A.Learning OpenCV：computer vision with the OpenCV library[M].Sebastopol：O’Reilly Media，Incorporated，2008：350-380.

[13]Zhang Z.A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22（11）：1330-1334.

[14]马颂德，张正友.计算机视觉：计算理论与算法基础[M].北京：科学出版社，1998：52-94.

[15]夏青元，徐锦法.三轴式无人旋翼飞行器及自适应飞行控制系统设计[J].航空学报，2013，34（3）：495-508.

ZHANG Liang,XU Jinfa

National Key Laboratory of RotorcraftAeromechanics,Nanjing University ofAeronautics&Astronautics,Nanjing 210016,China

According to the problem of target tracking for UAV,a target tracking and locating algorithm based on Camshift algorithm and binocular vision is proposed.The left and right images from binocular camera are used to calculate the central interesting point of the target with Camshift algorithm.After the central interesting point is reconstructed,the relative position and yaw angle between UAV and target under the body coordinate system are got.Data is optimized with the kalman filter. The estimated data is used as the flight control system loopback input data to achieve the autonomous tracking of UAV. The result of the experiment shows that the error of the algorithm is little.This algorithm has strong stability and accuracy.

Unmanned Aerial Vehicle（UAV）;binocular stereo vision;target tracking;locating

针对小型无人飞行器跟踪目标的问题，提出了一种基于双目视觉和Camshift算法的无人飞行器目标跟踪以及定位算法。双目相机得到的左右图像通过Camshift算法处理可得到目标中心特征点，对目标中心特征点进行三维重建，得到机体坐标系下无人飞行器与目标间的相对位置和偏航角，应用卡尔曼滤波算法对测量值进行了优化，将所得估计值作为飞行控制系统的反馈输入值，实现了无人飞行器自主跟踪飞行。结果表明所提算法误差较小，具有较高的稳定性与精确性。

无人飞行器；双目视觉；目标跟踪；定位

A

V249.1

10.3778/j.issn.1002-8331.1405-0263

ZHANG Liang,XU Jinfa.Target tracking and locating for UAV based on binocular stereo vision.Computer Engineering and Applications,2014,50（24）：27-31.

江苏高校优势学科建设工程资助项目。

张梁（1984—），男，博士研究生，研究领域为无人飞行器视觉导引与组合导航；徐锦法（1963—），男，博士，教授，研究领域为无人飞行器飞行控制与组合导航。E-mail：xjfae@nuaa.edu.cn

2014-05-21

2014-07-14

1002-8331（2014）24-0027-05

CNKI网络优先出版：2014-08-19，http∶//www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1405-0263.html