求解热传导系数反问题的量子行为粒子群算法

田 娜，朱龙超

1.江南大学 教育技术系，江苏 无锡 214122

2.中国船舶科学研究中心 信息技术室，江苏 无锡 214082

求解热传导系数反问题的量子行为粒子群算法

田 娜1，朱龙超2

1.江南大学 教育技术系，江苏 无锡 214122

2.中国船舶科学研究中心 信息技术室，江苏 无锡 214082

1 引言

热力学中的热传导系数，通常是通过对流或流体和固体之间的相变，来计算传热过程。对板表面的热传导系数精确地了解，在许多工程应用中都有很重要的作用，包括连铸坯和电子芯片的冷却[1]。

在过去的几十年里，许多工作已经致力于对随时间变化（时变）的热传导系数的研究[1]。Su和Hewitt[2]使用Alifanov迭代正则化方法来估计强对流流体在加热管外表面上沸腾时的热传导系数。在文献[3]中，三种版本的共轭梯度法用来估计平板表面的热传导系数，平板通过与降温液体的对流而散热。Chen和Wu[4]应用了一种包含拉普拉斯变换，有限差分和最小二乘法的混合策略，连同时间顺序的概念，三次样条和温度测量值一起，用于预测边界表面的热传导系数分布。Slodicka[5]采用边界元法和Tikhonov正则化来建构随时间变化的热传导系数。Chantasiriwan[6]采用顺序函数估计法连同线性基函数和线性变化的未来边界热通量或温度假设来估计随时间变化的Biot数字。在本文中，采用QPSO算法和Tikhonov正则化方法[7-9]用来估计时变热传导系数。QPSO算法是由Sun[10-12]在PSO的基础上提出的。PSO算法最初是由Kennedy和Eberhart提出的，是模拟鱼群和鸟群的社会行为的过程。与GA比较，PSO和QPSO的优点在于：有更少的参数需要控制，运行起来更简单，并且，算法只需要简单的算术运算符，而不需要像GA中选择，交叉，变异之类的操作。最后，结果与CGM估计得到的结果进行了比较。

2 问题描述

液体在平板的上面以一个恒定的温度流动[1]，如图1所示。

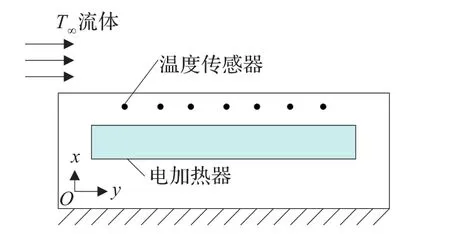
图1 电加热平板

如果平板突然被一个电加热器加热，板的温度会上升。假设平板的材料沿y轴均匀，对流边界条件在x=0和x=L是指定的。数学模型为：

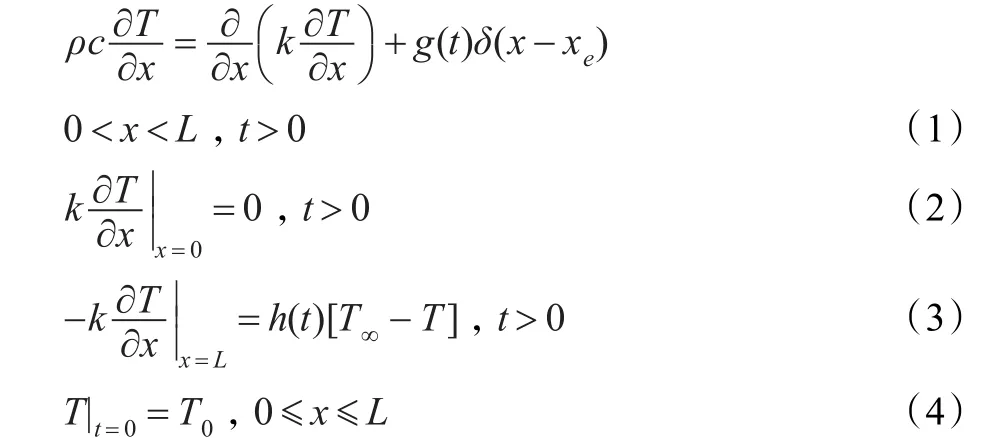
其中T(x，t)是在位置x和时间t的温度分布，g(t)是热源在x=xs的强度，T∞是周围环境的温度，T0是初始温度分布。为了描述简单，物理属性被设为K=ρC=L=1，这与采用无量纲的数据是一样的。在这里，h(t)是未知的待确定的热传导系数。对方程（1）采用隐式有限差分法：

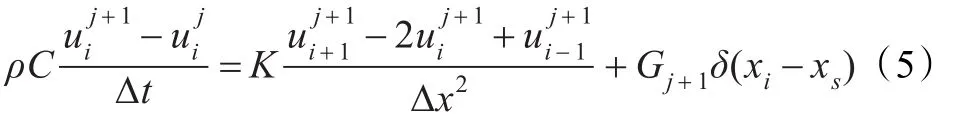
在边界x=L，对流边界条件用二阶离散得到：

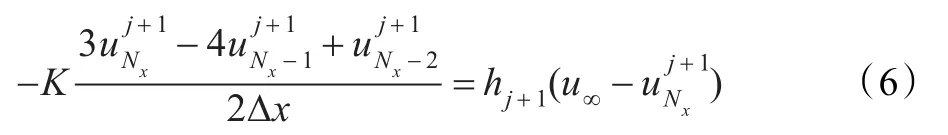
平均误差herror，用来评估估计得到的热传导系数，可以定义为：

其中Nt是时间步数，hj是估计得到的热传导系数，h~j是准确的热传导系数。

最小二乘模型用来求解此类反问题：

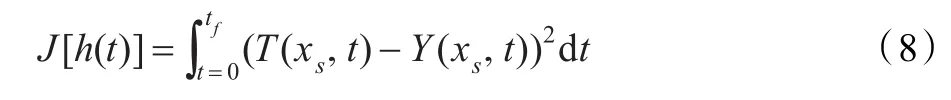
这种方法求解反问题的过程是不适定性的，不可避免的测量和计算误差常常导致不稳定和不精确的结果。所以，采用正则化技术来得到稳定解[7]，它可以将目标函数式（8）改写成如下适定形式：

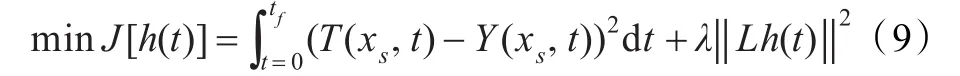
其中λ是正则参数，公式（9）右边第一项是差异项，第二项是正则项。正则项通常可以表示为如下形式：

其中n是正则阶数。常用的有零阶和一阶正则项。当n=0时，为零阶正则项：

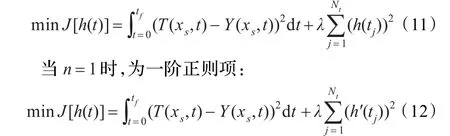
3 量子行为粒子群优化算法

3.1 粒子群优化算法

粒子群优化算法（PSO）是基于群体智能的优化技术，最初由Kennedy和Eberhart在1995提出的[13]。该算法的概念来源于鸟群或鱼群的社会行为。该系统有一个粒子群体，其中每个粒子代表一个优化问题可能的解。已经证明PSO算法与遗传算法（GA）有相当的性能[14]。

在有M个粒子，D维空间的原始PSO算法中，第i个粒子在第k次迭代步的位置向量和速度向量表示为：Xi(k)=(Xi1(k)，Xi2(k)，…，XiD(k))，Vi(k)=(Vi1(k)，Vi2(k)，…，ViD(k))。粒子根据以下迭代公式更新速度和位置：

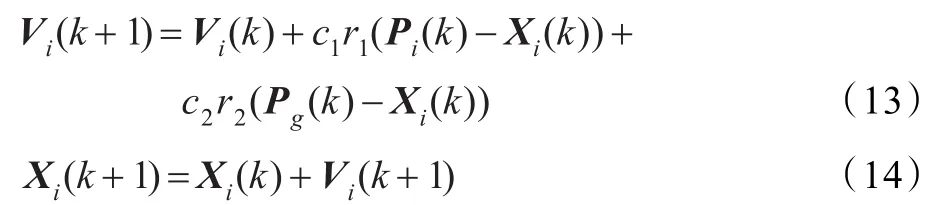
其中i=1，2，…，M ，j=1，2，…，D，c1和c2是加速系数。r1和r2是均匀分布在（0，1）中的随机数。向量Pi= (Pi1，Pi2，…，PiD)是第i个粒子的历史最佳位置。向量Pg=(Pg1，Pg2，…，PgD)是整个粒子群的历史最佳位置。

3.2 量子行为粒子群优化算法

原始PSO算法的缺点是不能确保收敛到全局最优解[15]，为了克服这个缺点，Sun在2004年提出了量子行为粒子群优化算法的概念，文献[10-11]中的轨迹分析说明，当每个粒子收敛到 pi=(pi1，pi2，…，piD)时，PSO算法实现收敛：

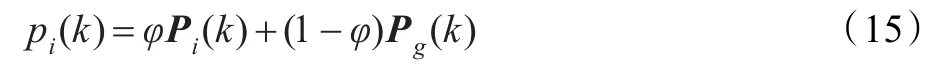
其中φ∈(0，1)。

在量子世界中，粒子的速度是没有意义的。所以在QPSO中，位置是唯一描述粒子状态的变量，更新公式如：

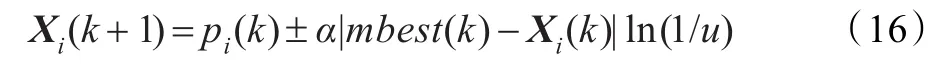
其中mbest(k)称作平均最优位置，定义为所有粒子历史最优位置的平均值：

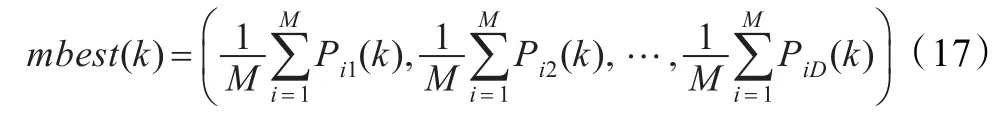
其中M是粒子的个数。公式（16）中的参数α是收缩系数，通过调整可以控制收敛速度。与PSO不同的是，QPSO算法不需要算法向量，并且只有一个参数需要控制，使得算法更容易执行。标准测试函数证明，QPSO算法的性能要优于PSO算法[10-12]。

在本文中，QPSO算法用来估计随时间变化的热传导系数h(t)，其中，每个粒子Xi(k)作为h(t)的一个候选解：

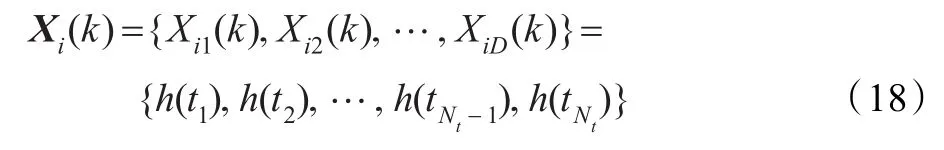
其中D=Nt。

QPSO与Tikhonov正则化方法估计h(t)的过程可以描述为：

选择N个正则参数值{λ1，λ2，…，λN-1，λN}以及与之对应的两个向量Residual和Norm；对于每一个正则参数 λj(j=1，2，…，N)

Step1初始化：粒子位置

X(0)={X1(0)，X2(0)，…，Xi(0)，…，XM(0)}

粒子历史最优位置

P(0)={P1(0)，P2(0)，…，Pi(0)，…，PM(0)}

全局最优位置Pg，缩放系数α=1.0，k=0。

Step2 while(k＜kmax)

根据公式（17）计算mbest；根据公式（15）计算 p；根据公式（16）更新每个粒子的位置；根据公式（12）评估每个粒子在λj下的适应值；更新P和Pg；更新α；

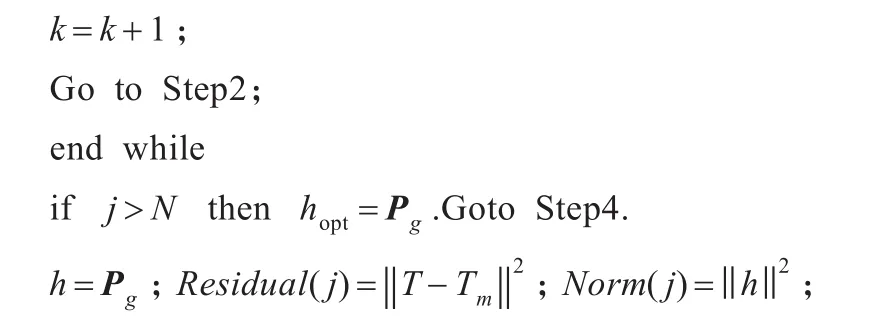
Step3将向量Residual和Norm的点画在坐标系中，以获得最优正则系数λopt。Go to Step1。

Step4输出估计得到的最优热传导系数hopt。

4 数值测试

在随后的数值实验中，采用方波函数[2]：

这是最难估计的一种情况。问题的设置为：

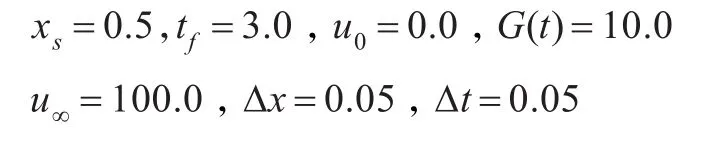
为了探讨传感器的数量和位置对结果的影响，表1列出了一系列不同的案例。图2显示了分别采用1，3，5个传感器的结果。从中可以注意到，用3个和5个传感器估计的结果并不优于只用一个传感器得到的结果。因此，这表明，一个传感器足以获得令人满意的估计问题。

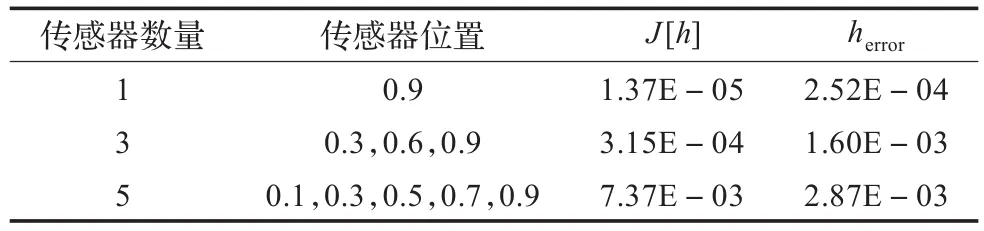
表1 传感器的数量和位置对结果的影响

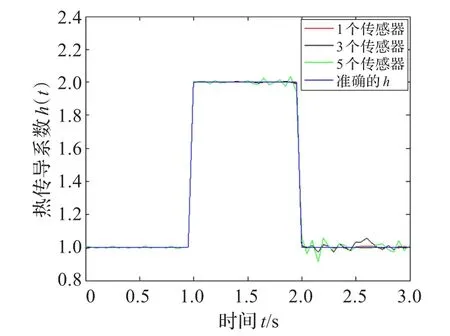
图2 QPSO用不同数量的传感器估计的h(t)

因此，在随后的测试中只用一个传感器来进行温度测量。图3所示显示了传感器的位置对热传导系数的影响。表2列出了四种传感器的位置和其相应的平均误差和目标函数值。从中可以注意到，传感器越接近对流边界，结果越好，如图3所示。

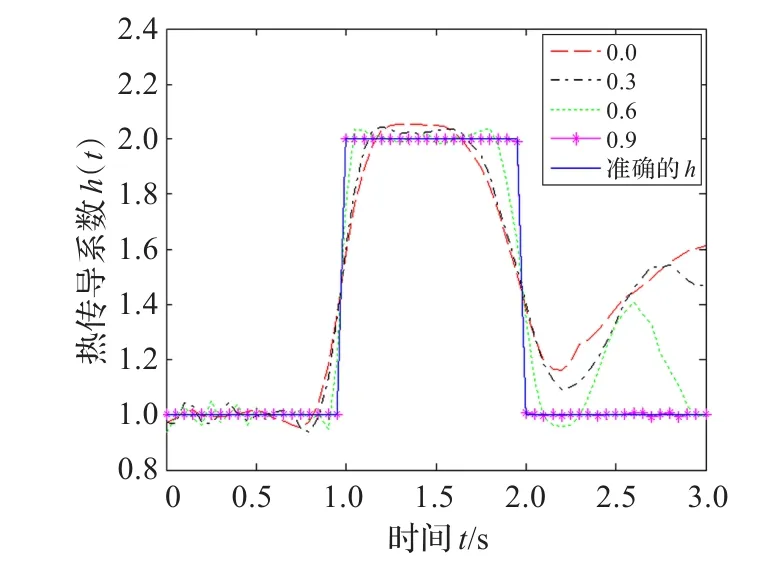
图3 QPSO采用不同位置的传感器估计的h(t)

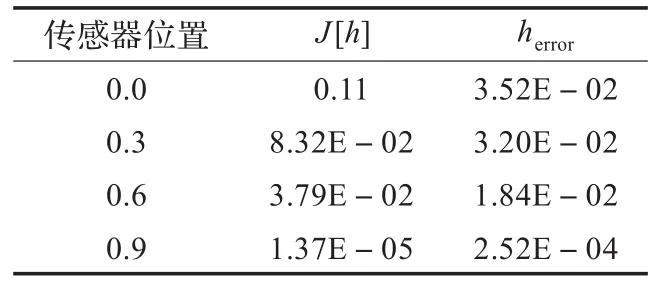
表2 传感器位置对结果的影响

用模拟实验温度来研究不同噪音水平对结果的影响。测试中采用了三个不同的噪声水平。表3列出了QPSO和CGM算法的平均误差和目标函数值。图4比较了二者的结果。从中注意到，由QPSO估计得到的出色结果，特别是对t=tf附近值的估计。图5显示了QPSO和CGM在估计热传导系数时的收敛曲线。注意到，CGM收敛速度很快，但是在一些迭代步之后，收敛就出现了停滞。虽然随机初始化的QPSO算法的收敛速度相对缓慢，但是全局最优解得到了保障。

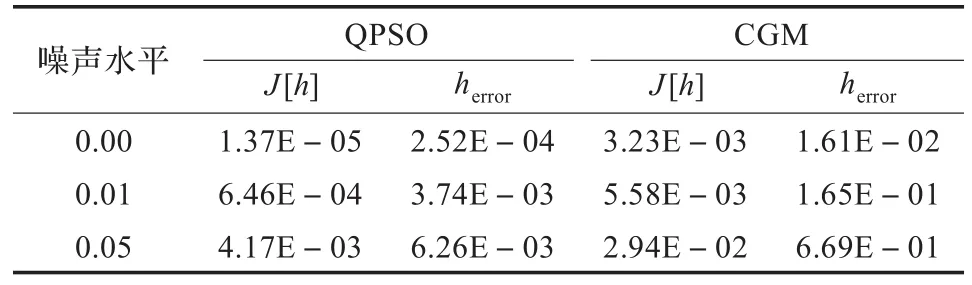
表3 在不同噪声下QPSO和CGM的比较

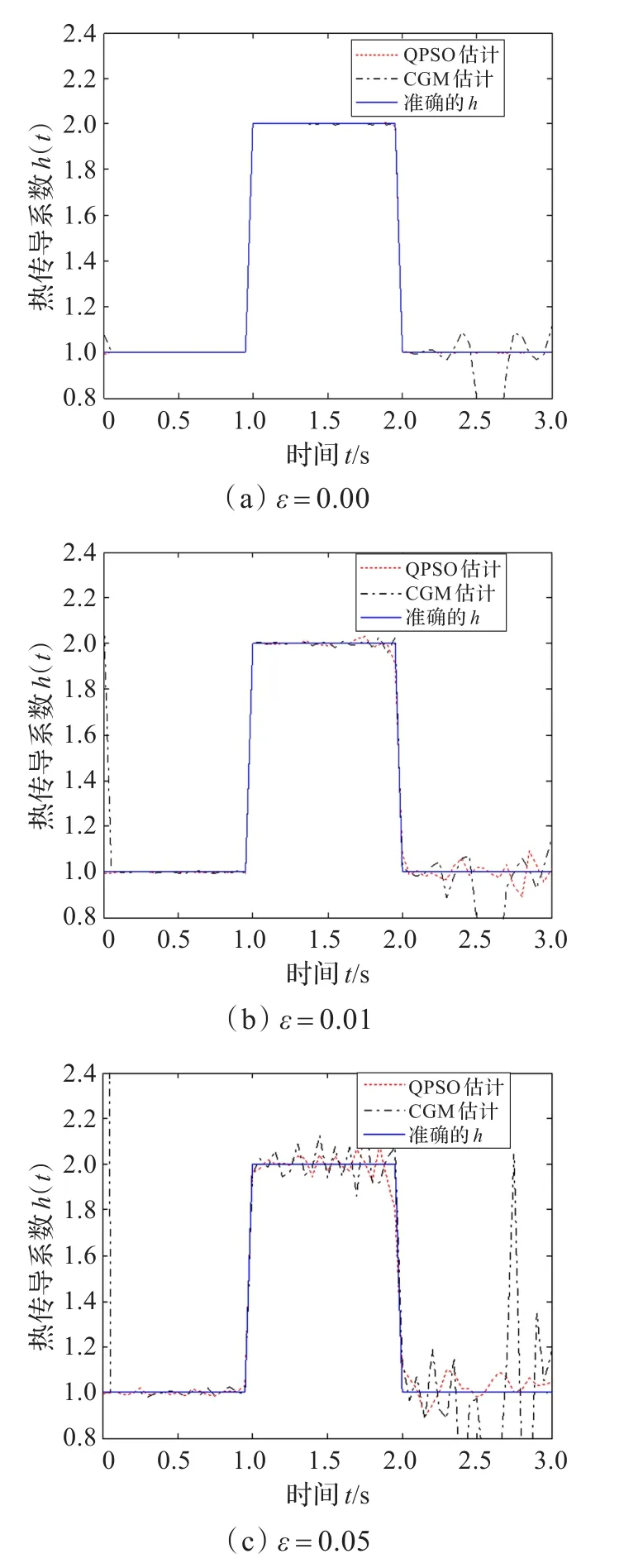
图4 QPSO和CGM用不同水平的噪声估计的h(t)

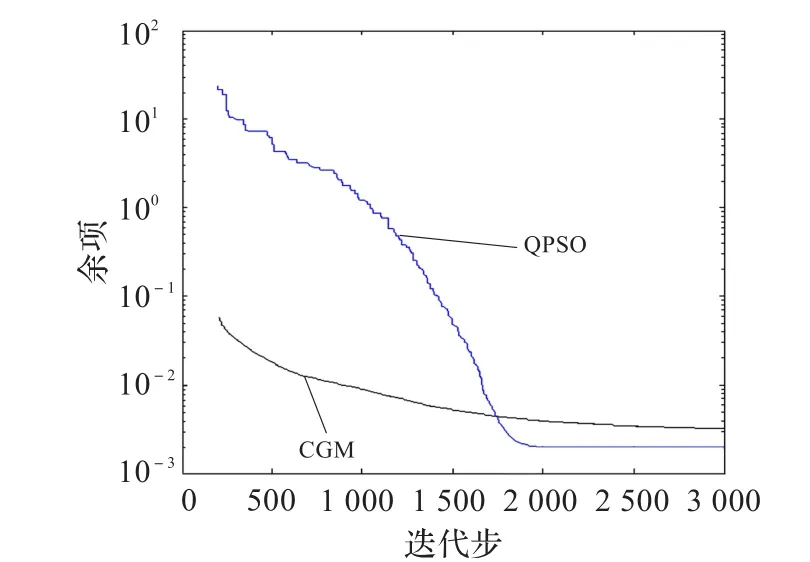
图5 CGM和QPSO估计的h(t)收敛曲线(ε=0)

为了测试QPSO算法的鲁棒性，再对两个函数进行测试，一个是持续很短时间的方波函数：

由QPSO和CGM估计的结果如图6和图7所示。可以看出，由QPSO估计的时变热传导系数与准确的热传导系数非常逼近。

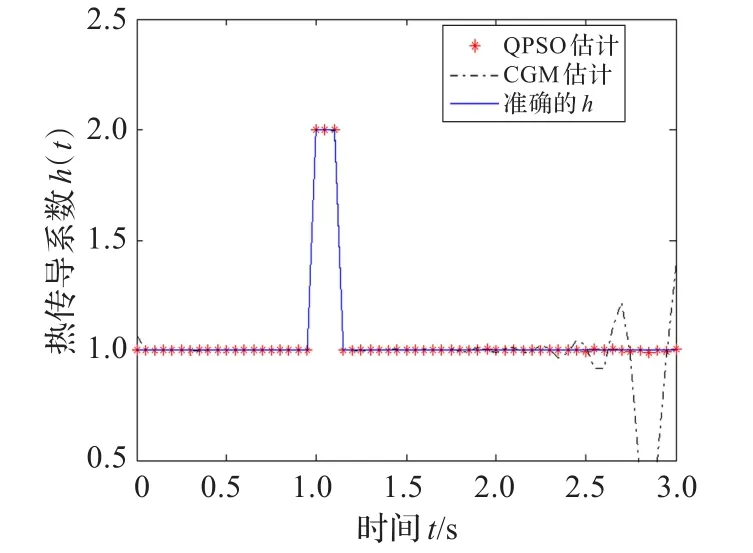
图6 QPSO和CGM估计较小波函数的h(t)

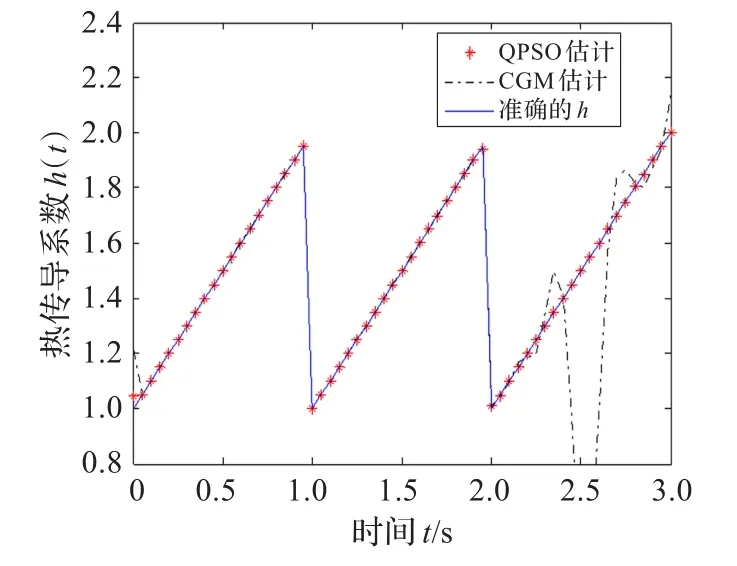
图7 QPSO和CGM估计波形h(t)(ε=0)

5 结论

在本文中，QPSO算法用来对平板表面的时变热传导系数进行估计。采用模拟测量温度值得到的结果证明了QPSO算法的可行性和稳定性。分析研究了传感器的数量和位置对结果精确度的影响。通过对QPSO和CGM的比较，说明了QPSO的优越性。

[1]Beck J V，Blackwell B，St-Clair C R.Inverse heat conduction：ill-posed problems[M].New York：Wiley-InterScience，1985.

[2]Su J，Hewitt G.Inverse heat conduction problem of estimating time-varying heat transfer coefficient[J].Numerical Heat Transfer Part A：Applications，2004，45（8）：777-789.

[3]Colaco M J，Orlande H R B.Comparison of different versions of the conjugate gradient method of function estimation[J].Numerical Heat Transfer Part A：Applications，1999，36（2）：229-249.

[4]Chen H T，Wu X Y.Investigation of heat transfer coefficient in two-dimensional transient inverse heat conduction problems using the hybrid inverse scheme[J].International Journal for Numerical Methods in Engineering，2008，73（1）：107-122.

[5]Slodicka M，Lesnic D，Onyango T T M.Determination of a time-dependent heat transfer coefficient in a nonlinear inverse heat conduction problem[J].Inverse Problems in Science and Engineering，2010，18（1）：65-81.

[6]Chantasiriwan S.Inverse heat conduction problem of determining time-dependent heat transfer coefficient[J].International Journal of Heat Mass Transfer，2000，42（23）：4275-4285.

[7]Tikhonov A N，Arsenin V Y.Solution of ill-posed problems[M].Winston：Washington DC，1977.

[8]Morozov V A.Methods for incorrectly posed problems[M]. [S.l.]：Springer，1984.

[9]Hansen P C.The L-curve and its use in the numerical treatment of inverse problems[M]//Computational Inverse Problem in Electrocardiography，Advances in Computational Bioengineering.Holland：WIT Press，2001.

[10]Sun J，Feng B，Xu W B.Particle swarm optimization with particles having quantum behaviour[C]//IEEE Congress on Evolutionary Computation，Portland，USA，2004.

[11]Sun J，Xu W B，Liu J.Parameter selection of quantumbehaved particle swarm optimization[C]//Lecture Notes in Computer Science，2005，3612.

[12]Sun J，Xu W B，Feng B.A global search strategy of quantum-behaved particle swarm optimization[C]//IEEE Conf on Cybernetics and Intelligent Systems，Singapore，2004.

[13]Kennedy J，Eberhart R C.Particle swarm optimization[C]// IEEE Int Conf on Neural Networks，Perth，Australia，1995.

[14]Eberhart R C，Shi Y.Comparison between genetic algorithm and particle swarm optimization[C]//Lecture Notes in Computer Science：Evolutionary Programming VII. Berlin，Heidelberg：Springer，1998，1447：611-616.

[15]van den Bergh F.An analysis of particle swarm optimizers[D].South Africa：University of Pretoria，2001.

[16]Clerc M，Kennedy J.The particle swarm：explosion，stability，and convergence in a multi-dimensional complex space[J].IEEE Transactions on Evolutionary Computing，2002，6（1）：58-73.

TIAN Na1,ZHU Longchao2

1.Department of Educational Technology,Jiangnan University,Wuxi,Jiangsu 214122,China
2.Department of Information Technology,China Ship Science Research Centre,Wuxi,Jiangsu 214082,China

In this paper,the Quantum-behaved Particle Swarm Optimization（QPSO）with Tikhonov regularization is used to solve the inverse heat conduction problem of estimating the time dependent heat transfer coefficient of a flat plate.The prior information about the functional form of the unknown is unavailable.The estimation is based on transient temperature measurements taken by the sensors imbedded in the plate,which are used in the least square model,minimized by QPSO. The detail of choosing the best regularization parameter by L-curve method is presented.Numerical experiments are performed to test the proposed method.Effects of the location and number of sensors are also investigated.Comparison with conjugate gradient method is given as well.

heat transfer coefficient;Quantum-behaved Particle Swarm Optimization（QPSO）;Tikhonov regularization; conjugate gradient method;L-curve

量子行为粒子群优化算法（QPSO）和Tikhonov正则化方法用来求解热传导反问题，近似估计平板随时间变化的热传导系数。由于热传导系数的函数形式是未知的，所以问题可以归结为函数估计问题。求解过程是基于最小二乘模型的，采用的是嵌在平板中的传感器所测量得到的温度，优化过程由QPSO算法来求解。给出了由L曲线方法选择正则参数的详细过程。提出算法的有效性经过了数值实验的验证。传感器的位置和数量对结果的影响也做了研究。给出了与共轭梯度法的比较。

热传导系数；量子行为粒子群优化算法；Tikhonov正则化；共轭梯度法；L曲线

A

TP391

10.3778/j.issn.1002-8331.1305-0033

TIAN Na,ZHU Longchao.Estimation of heat transfer coefficient using Quantum-behaved Particle Swarm Optimization.Computer Engineering and Applications,2014,50（24）：266-270.

江南大学自主科研项目基金（No.1245210382130120，No.1242050205142810）。

田娜（1983—），女，博士，副教授，主要研究方向为智能计算，模式识别，偏微分方程反问题。

2013-05-08

2013-09-11

1002-8331（2014）24-0266-05

CNKI网络优先出版：2014-05-05，http∶//www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1305-0033.html