基于模糊积分的供应链网络优化方法

张国防，何莉辉

河北大学 数学与计算机学院，河北 保定 071002

基于模糊积分的供应链网络优化方法

张国防，何莉辉

河北大学 数学与计算机学院，河北 保定 071002

1 引言

从供应链角度而言，成功选择合作伙伴至关重要，供应链网络设计中最主要的任务就是优势企业依据技术、质量、成本、时间、产能等特性，从每一层次候选企业中选择良好的合作伙伴，从而确定产品从原材料起点到顾客端点的整个流程网络。文献[1]提出了基于自我分类理论的供应链合作伙伴选择的两阶段模型。该模型提出了供应链合作伙伴选择应在企业去人格化后，在自我分类的基础上选择与核心企业核心能力互补且具有竞争力的合作伙伴的观点，为供应链合作伙伴选择提供了新思路。文献[2]从供应链合作伙伴选择角度出发，讨论了基于GBOM的供应链网络的结构，在此基础上建立了供应链合作伙伴选择的数学模型，给出了模型的求解方法。文献[3]选择最小二乘支持向量机（LS-SVM）算法对合作伙伴进行选择。传统供应链网络设计问题的研究中，文献[4]利用模糊事件的可信性测度推导零售商的模糊期望利润，运用logit模型刻画消费者的随机选择行为，借助有限维变分不等式理论构建具有模糊需求的多商品流供应链网络均衡状态满足的变分不等式。而在文献[5]中，研究了供应商向制造商供应原材料，生产同质产品的制造商通过零售商销售渠道将其产品销售给消费者，以满足消费市场随机需求的供应链网络最优化问题。然而在供应链网络设计时所依据的数据大多是模糊与随机双重不确定性的。诸多的模糊和随机双重不确定性给供应链网络构建带来了困难。因此本文引入模糊理论和随机理论研究供应链合作伙伴选择与网络构建方法。

在实际的决策过程中，由于客观事物的复杂性、随机性及人类思维的模糊性，决策者在对事物进行判断评估时，提供的偏好信息有可能无法采用精确的数值来进行估计，一般喜欢直接用模糊和随机双重语言形式给出，决策者对不同类别属性的综合过程带有很强的主观思考或经验推理，所以这也是一个对离散信息、带有随机性和模糊偏好的模糊综合过程。文献[6]利用博弈理论构建了分散式控制生产商与零售商的Stackelberg博弈模型和集中式控制闭环供应链的决策模型，通过求解模型得到了各成员企业和闭环供应链的最优决策及利润。文献[7]利用模糊理论的期望值模型，分别在集中式和分散式两种决策方式下给出了新产品的最优批发价格、最优零售价格及废旧产品的最优回收率的解析表达式。但是上述方法中所使用的决策工具只考虑了单个属性的重要程度，没有考虑属性之间的交互性对整个决策的影响。因此本文引入模糊测度和模糊积分理论研究供应链合作伙伴评价与选择的多重多属性模糊综合决策，以及模糊随机环境下的任务粗分配方法。下面对本文使用的gλ模糊测度和choquet模糊积分做简单的介绍[8]。

2 gλ模糊测度与choquet模糊积分

2.1 gλ模糊测度

本文中，供应链合作伙伴选择与网络构建中涉及的是有限个属性，讨论的内容主要是基于有限集合，所以假定有限集合 X={x1，x2，…，xn}，有限集上的模糊测度在数学中的定义如下：

定义1假设 X为非空集合，P(X)为由 X的子集构成的幂集，集函 μ∶P(X)→[0，1]满足下面的三个性质时，称为定义在P(X)上的模糊测度：

（1）μ(∅)=0，μ(X)=1（归零性，正则性）

（2）A∈P(X),B∈P(X),B⊂A⇒μ(B)≤μ(A)（单调性）

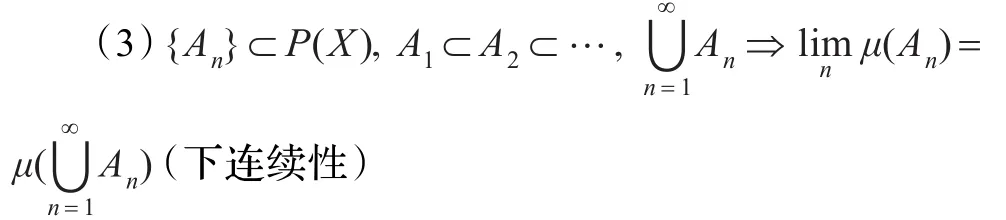
定义2如果模糊测度g还满足下面性质时，那么称之为gλ-模糊测度（Sugeno模糊测度）。

存在常数λ，λ＞-1，使得：

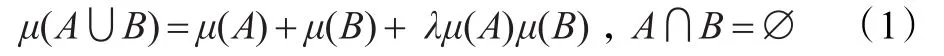
通常将 gλ-模糊测度记为 g，令 g({xi})=gi，i=1，2，…，n，xi∈X，称gi为模糊密度。模糊密度gi可以解释为供应链合作伙伴选择与网络构建中第i个属性的重要程度。关于gλ-模糊测度有下面两个重要的结论：

定理1设 g为定义在 P(X)上的 gλ-模糊测度，A1，A2，…，Al为P(X)中互不相交的l个集合(0＜l≤2n= |P(X)|)，则

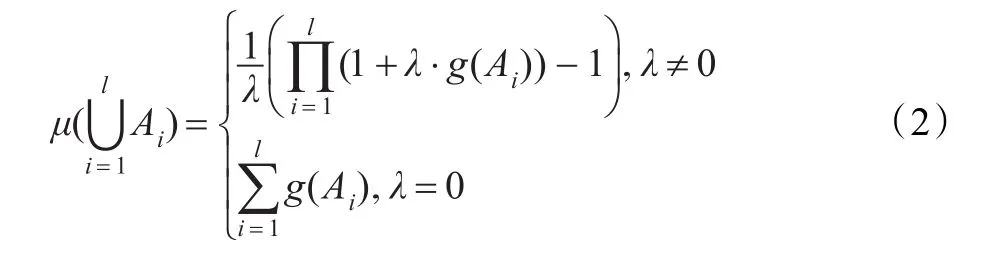
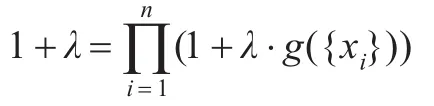
由定理1和定理2可知，模糊测度 g在集合 X= {x1，x2，…，xn}中每一单点集的模糊测度值能确定 g在P(X)中其他集合的模糊测度值，因此在供应链合作伙伴选择与网络构建中，要确定gλ-模糊测度，只需知道模糊密度，即只要确定各个属性的重要度就可以了。

2.2 choquet模糊积分

定义3假设 f为定义在 X上的非负函数，μ为定义在F上的模糊测度，F为由X的子集构成的σ-代数（当X为有限集合时，F=P(X)），则 当X={x1，x2，…，xn}为有限集合时，令·(i)满足条件：

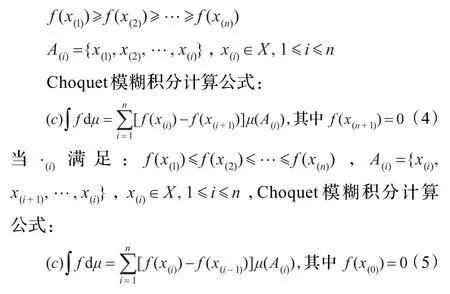
3 基于模糊积分的合作伙伴选择模糊多属性综合决策

3.1 供应链合作伙伴评价属性模糊随机变量和随机模糊变量

本文以文献[9]中提供的供应链合作伙伴评价多属性层次分析结构模式为依据研究模糊和随机双重不确定性环境下的合作伙伴选择。在模糊与随机双重不确定性环境下得到的各属性分量的参数值均为模糊随机数值，或为随机模糊数值，或为定量绝对模糊随机数，或为定性随机模糊语意。属性变量取值为模糊随机型时，首先将模糊语意与相应的定义于[0，1]的模糊三角数或模糊区间数匹配，进行数量化转换，然后根据模糊随机型取值的概率分布计算出期望值作为最终参与决策的数值。属性变量取值为随机模糊型时，首先依据随机性计算出期望值，然后将模糊语意与相应的定义于[0，1]的模糊三角数或模糊区间数匹配，进行数量化转换。

3.2 离散信息各属性及属性子集模糊测度的确定

根据前面的叙述，只要确定出各个单个属性的重要度，即测度值，那么由公式（2）可以完全确定gλ模糊测度，这样属性子集的测度值给出了属性之间交互性的一种度量。接下来的问题是如何将这些模糊语意量子在不确定性最小情况下转换为相应的单个属性的重要度。由于模糊语意量子具有单调性，故模糊语意决策的属性重要度向量由下式确定[10]：

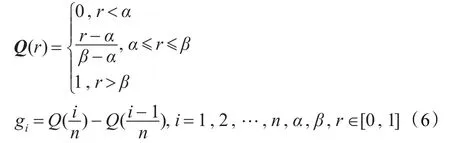
为了评价决策者在模糊语意下的决策状态，给出相应属性重要度向量的orness（或的程度）和entropy（熵）两种测度，即

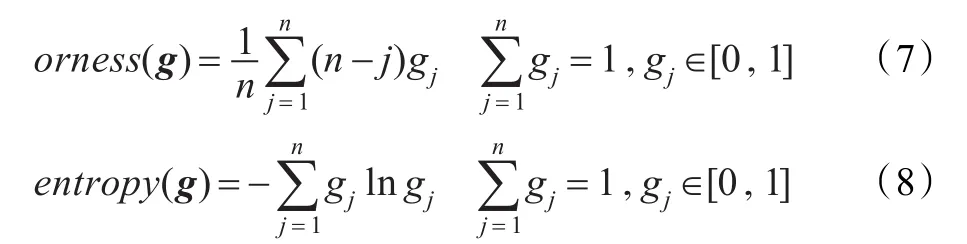
在多属性决策中如何确定各属性的重要度向量，为了尽量减小各属性重要度系数的不确定，根据Jaynes最大熵原理[11]，所确定的属性重要度向量应使entropy取极大。结合文献[12]中的方法，假设在供应链合作伙伴选择与网络构建中有n个属性用gi，(i=1，2，…，n)表示模糊密度，即 gi=μ({x(i)})，为单个属性重要程度的度量，X={x1，x2，…，xn}表示n个属性集合。gλ模糊测度测度确定步骤如下：

步骤1由式（6）得到属性重要度初始向量 g= (g1，g2，…，gn)。

步骤2由式（7）计算属性重要度向量g的orness(g)值。

确定模糊测度值。

3.3 基于模糊积分的模糊多属性综合决策

本文采用文献[9]中的供应链关系关联度定义，结合模糊测度的确定方法，由属性重要性程度与决策过程信息取舍多少模糊语意进行匹配可以确定不同属性的重要度，以choquet模糊积分作为决策工具对各个属性子集进行信息融合，得到各个属性的数值信息。所以，合作伙伴选择的决策过程如下：

步骤1优势企业（盟主）所委托或指定的决策专家小组根据产品类型、生产任务、供应链策略等提出伙伴企业选择评价的属性，对大的属性可继续分解为具体的实施细则即相应的子属性，依AHP模式建立比较全面、详细的评价属性体系。

步骤2采用交互方式，依据评价指标体系充分征询候选企业，分别采集候选企业对其上游企业或下游企业选择的子属性评价信息。通过对所采集的信息可进一步对AHP评价多属性体系进行修正和完善。

步骤3对采集得到的定量子属性信息和定性子属性信息进行模糊语意转化为相应的模糊数，对信息进行规范化处理。

步骤4根据多属性体系中属性或子属性的向量个数，分别对综合决策中的三种模糊语意：至少一半、绝大多数、尽可能多，利用gλ模糊测度测度确定步骤计算得到各个属性的重要度以及属性子集的重要度。

步骤5根据产品类型、生产阶段和供应链策略，对AHP结构中的属性按重要性程度进行分类，即哪些属性为关键属性，哪些属性为重要属性，哪些属性为一般属性。按关键属性与至少一半匹配、重要属性与绝大多数匹配、一般属性与尽可能多匹配，以choquet模糊积分作为信息决策工具对各个属性下的子属性信息进行融合，得到各属性数值信息。再按“绝大多数专家意见一致”这一语意进行属性信息融合，得到伙伴关系选择优属度。

步骤6对相邻层次上两候选企业对各自对方的伙伴关系优属度按乘积整合，得到两两候选企业间的伙伴关系关联度。相邻层次上伙伴关系关联度应进行归一化处理，最后数值大小表示合作伙伴关系选择的优先顺序。

4 面向任务预分配的供应链网络

设一定时期内产品的市场需求总量为Q，供应链各层间的物料转换关系为1。考虑各个企业的生产处理能力的约束。如果这些约束参量是模糊随机的，且市场需求总量也是模糊随机的，这时可以用模糊随机规划的期望值模型，并以伙伴关系关联度作为任务分配的权重。

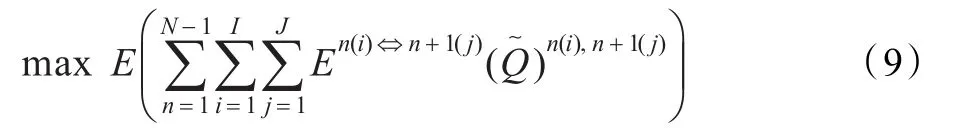
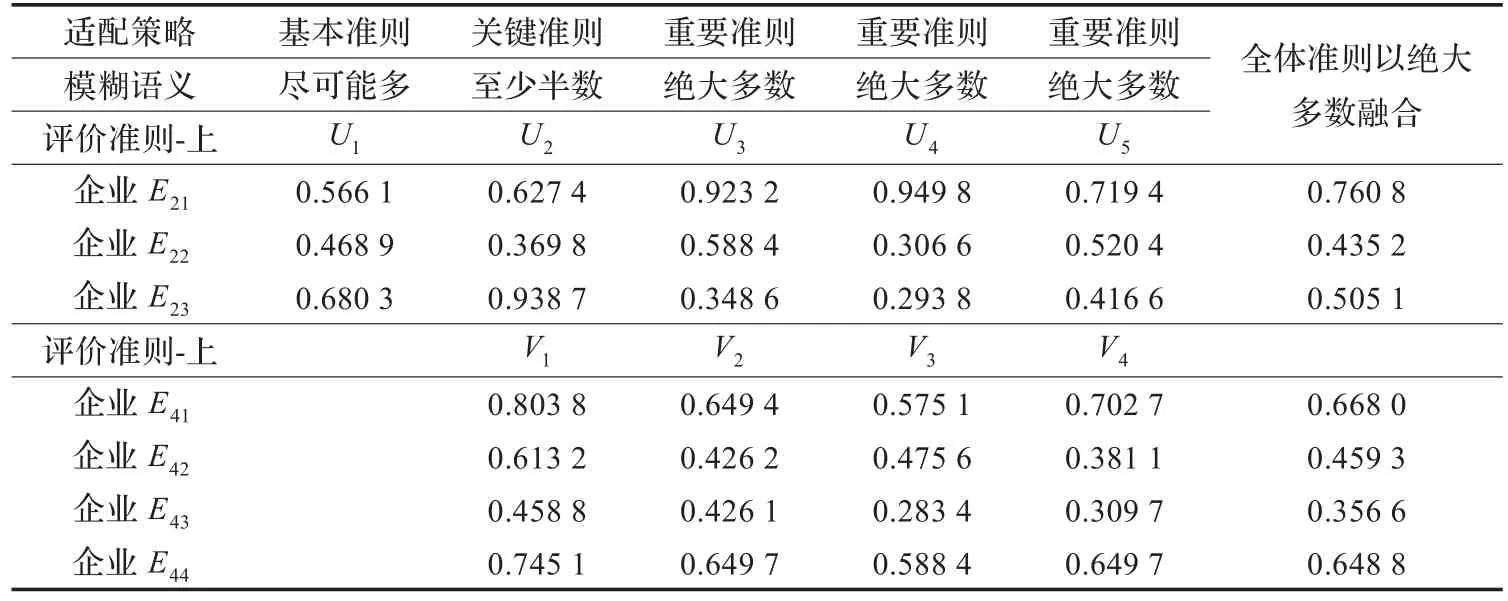
表1 评价时各准则适配策略和相应数据的模糊积分决策结果

其中：式（10）（11）为企业的能力约束，式（12）为节点企业的物流约束，式（13）为需求约束。

为了求解上述模糊随机规划，参照文献[13]中的方法，结合文献[14-15]中的思路，采用由模糊随机模拟，神经网络及遗传算法相结合而成的混合智能方法，其步骤如下：

步骤1通过模糊随机模拟为不确定函数U产生输入输出数据。

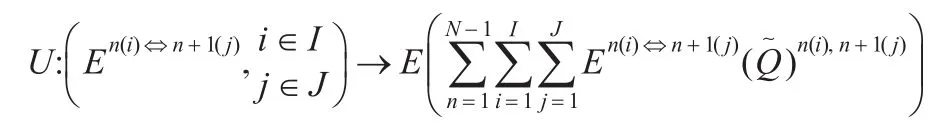
步骤2利用产生的数据训练一个神经网络逼近不确定函数。

步骤3初始产生群体，并利用训练好的神经网络检验群体中个体的可行性。

步骤4通过交叉和变异操作跟新群体，并利用训练好的神经网络检验子代中个体的可行性。

步骤5利用训练好的神经网络计算所有个体的目标值。

步骤6根据目标值计算每个个体的适应度。

步骤7通过轮盘赌方法选择个体。

步骤8重复步骤4到7直到完成给定的循环次数。

步骤9给出最好的个体作为最优解。

5 事例模拟

应用事例以某市轻纺区域网络化制造为背景，考察某三个集团公司，该三个集团以生产加工运动服为主，利用本文提出的方法进行供应链构建与优化模拟，与文献[3]、文献[9]和文献[13]中提出的方法进行对比，取五层{1-3-3-4-3}供应链网络拓扑，以{N1-N2-N3-N4-N5}表示第一层企业 E11一家，第二层企业{E21，E22，E23}三家，第三层企业{E31，E32，E33}三家，第四层企业{E41，E42，E43，E44}四家，第五层企业{E51，E52，E53}三家。在供应链网络构建过程中，首先进行的是合作伙伴评价与选择，按决策流程评价准则，依照这些评价准则，各企业分别对各自上下游可合作伙伴进行评价。根据供应链策略确定各评价准则的重要性程度见表1。设一定时期内产品的市场需求总量为确定值，分别利用文献[3]、文献[9]、文献[13]和本文提出的方法构建供应链网络，以最终网络的分配总量在市场需求总量中的比重为标准，实验结果见表2。通过对实验结果的分析，可以看出使用本文提出的方法较其他方法具有很好的结果，其主要原因是考虑属性之间的交互作用，同时利用choquet模糊积分为决策工具可以将各个属性之间的交互性进行有效的处理，这样就尽可能地利用了数据提供的信息，保证较好的结果。

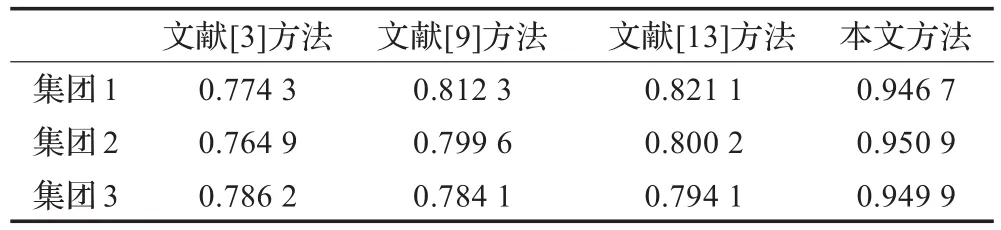
表2 各种方法得到的分配总量在需求总量中的比重结果

6 结论

本文分析了模糊与随机双重不确定环境下合作伙伴选择与供应链网络构建，给出了相应的基于模糊测度和模糊积分理论的决策模型。针对供应链合作伙伴多属性评价与决策，采用模糊随机变量和随机模糊变量刻画多属性中定性参量与定量参量的模糊与随机双重不确定性，研究了基于供应链策略导向的模糊随机多属性数值融合与模糊综合决策，还研究了以合作伙伴关系关联度为依据，采用模糊随机规划期望值模型探讨了面向任务预分配的供应链初始网络确定方法，最后通过事例模拟进行了验证。

[1]刘家国，赵金楼.基于自我分类的供应链合作伙伴选择模型[J].哈尔滨工程大学学报，2011（6）.

[2]单汨源，兰海丰，毛超.基于GBOM的供应链合作伙伴选择[J].统计与决策，2011（12）.

[3]肖宇，朱敏，黄俊.基于LS-SVM的供应链合作伙伴选择[J].计算机与数字工程，2010（9）.

[4]胡劲松，徐元吉，刘芳霞，等.具有模糊需求的多商品流供应链网络均衡研究[J].控制与决策，2012（5）.

[5]张桂涛，孙浩，胡劲松，等.考虑风险的随机需求供应链网络均衡研究[J].复杂系统与复杂性科学，2012（4）.

[6]徐兵，吴明.双营销渠道闭环供应链决策模型与协调[J].西南交通大学学报，2012（6）.

[7]魏杰，马茜，张新军，等.模糊环境下闭环供应链定价决策研究[C]//中国自动化学会控制理论专业委员会C卷，第三十届中国控制会议，2011.

[8]王熙照.模糊测度与模糊积分及在分类技术中的应用[M].北京：科学出版社，2008.

[9]傅玉颖.不确定情况下基于模糊集理论的库存管理研究[J].系统工程理论与实践，2005（9）.

[10]Herrera，Francisco，Martinez L.A 2-tuple fuzzy linguistic representation model for computing with words[J].IEEE Transactions on Systems，Man，and Cybernetics，2000，6：746-752.

[11]朱雪龙.应用信息论基础[M].北京：清华大学出版社，2001.

[12]Filev D，Yager R R.Analytic properties of maximum entropy OWA operators[J].Information Sciences，1995，85：11-27.

[13]刘宝啶，赵瑞清，王纲.不确定规划及应用[M].北京：清华大学出版社，2003.

[14]陈倩.区间模糊语言多属性群决策方法及应用研究[J].计算机工程与应用，2012，48（33）：18-23.

[15]田卫东，张建良.证据理论与模糊距离不确定性信息融合方法[J].计算机工程与应用，2011，47（30）：148-151.

ZHANG Guofang,HE Lihui

College of Mathematics and Computer Science,Hebei University,Baoding,Hebei 071002,China

In this paper,some problems are represented under the fuzzy-random uncertain circumstances,which usually happen when cooperation partner is selected in supply chain management.Furthermore,three methods are proposed∶the first one is selection of cooperation partner of supply chain,the second one is construction way of supply chain networks, the last one is the rough allocation of task under fuzzy-random uncertain circumstances.In these methods,the important technology is the policy of supply chain management and the tool of decision is fuzzy integral.A simulation example is represented,which shows that the proposed methods are feasible.

supply chain;fuzzy-random;fuzzy measure;fuzzy integral

分析了模糊随机双重不确定性环境下供应链合作伙伴选择时存在的问题，提出了由供应链策略为主导，以模糊积分为决策工具的模糊随机多重多属性供应链合作伙伴选择与网络构建方法，以及模糊随机环境下的任务粗分配方法。通过事例模拟进行了验证，结果表明所提方法有效可行。

供应链；模糊随机；模糊测度；模糊积分

A

TP181

10.3778/j.issn.1002-8331.1305-0149

ZHANG Guofang,HE Lihui.Method based on fuzzy integral about construction and optimization of supply chain networks.Computer Engineering and Applications,2014,50（24）：231-235.

河北大学青年基金（No.2011Q12）。

张国防（1979—），男，讲师，研究领域为机器学习、人工智能；何莉辉（1979—），通讯作者，女，讲师。E-mail：helihui@hbu.cn

2013-05-14

2013-06-30

1002-8331（2014）24-0231-05

CNKI网络优先出版：2013-09-12，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130912.1436.011.html

book=235,ebook=240