Bernoulli多项式Bn(x)与第二类Stirling数S2(n,k)的关系*1

李 晓 冬

(包头师范学院 数学科学学院，内蒙古 包头 014030)

Stirling数和Bernoulli数在分析、组合数学、数论及近似计算等方面均有广泛应用。一直以来是人们感兴趣的研究课题，Bernoulli数是18世纪由瑞士数学家Jakob Bernoulli所定义。Stirling数的概念，由James Stirling于1730年提出的，并在他的著作《Methodus Differentialis》中首次使用。1933Ch.Jordan在他的一篇论文中对Stirling数做了彻底的阐述，并给出了一些Stirling数重要性质。本文主要目的是在Bernoulli数与第二类Stirling数关系的基础上,获得包含 Bernoulli 多项式Bn(x)、第二类Stirling 数的恒等式。

1 Stirling数

定义1：设x为实变元，令(x)0=1，(x)n=x(x-1)(x-2)…(x-n+1)(n=1,2,…)。

(x)n叫做实变元x的n次降阶乘，显见(x)n是x的n次多项式。以S1(n,k)表示(x)n的展开式中xk的系数，S1(n,k)称为第一类Stirling数。

定理1：xn可由(x)0,(x)1,…,(x)n线性表出且表示法唯一。

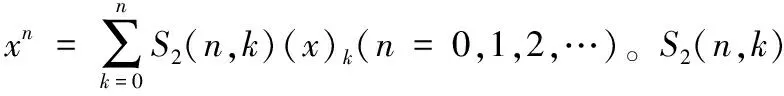
定义3：令ΔmOr=Δmnr|n=0,ΔmOr称为零的差分。

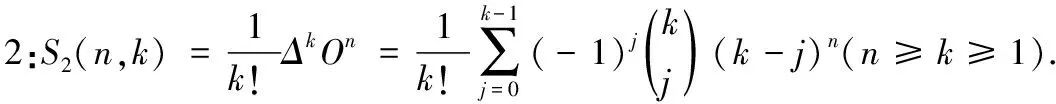
2 Bernoulli数及Bernoulli多项式

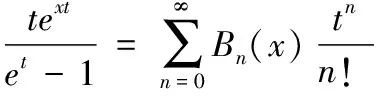
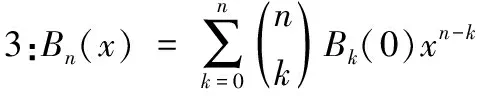
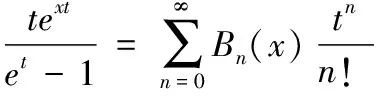
(1)

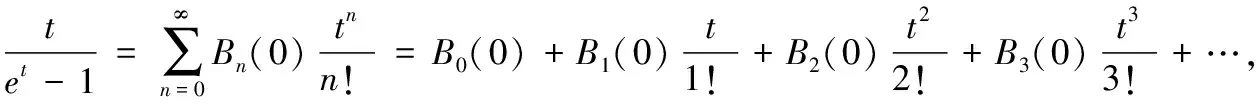
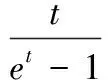
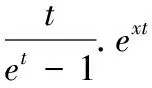
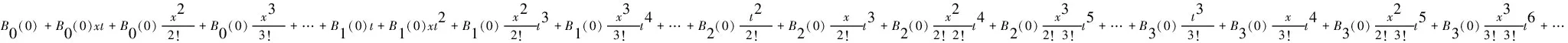
定理4:当n>1时，有B2n+1=B2n+1(0)=0.

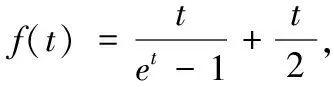
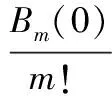
定理5:求当n很小时候的Bernoulli数Bn,根据

有

另一方面，有

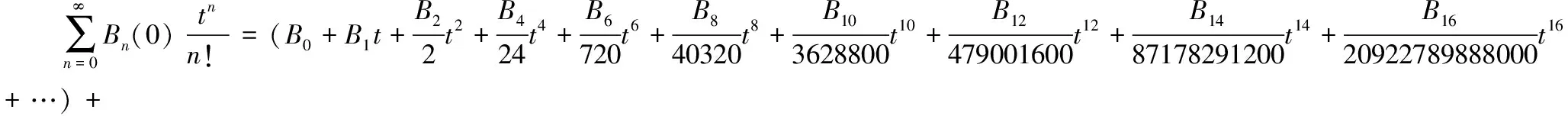
注意到定理4中所述的B3=B5=B7=…=0，比较二者的系数可知：

定理6:试求低价的Bernoulli多项式

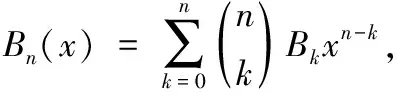
B0(x)=B0(0)=B0=1,

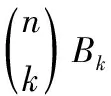
3 S2(n,k)与Bn(x)的关系

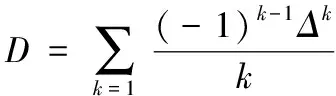
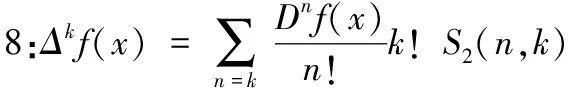
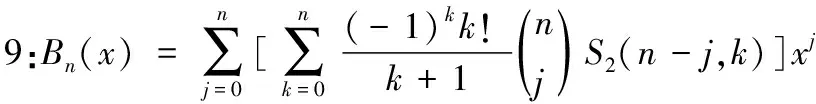
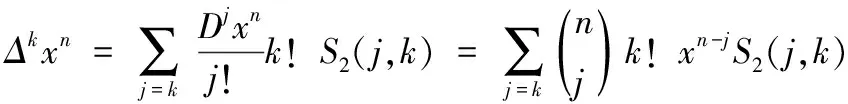
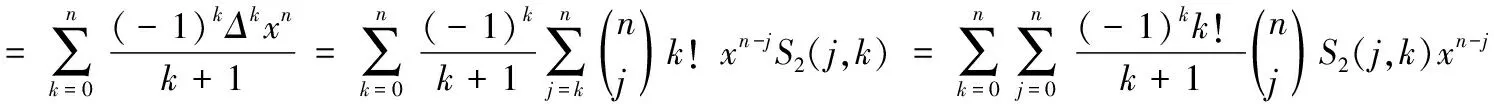
〔参考文献〕

[1]曹汝成.组合数学[M].广州:华南理工大学出版社 1999.

[2]刘建军 与Bernoulli数相关的一组计数恒等式 [J].辽宁大学学报(自然科学版),2002，29(4)，301—303.

[3]黄清.Bernoulli多项式的性质和计算 [J].杭州师范学院学报,2000，6，43-46.

[4]李晓冬.Bernoulli数Bn与第二类Stirling数S2(n,k)的关系[J].太原师范学院学报,2011，4,29-31.

[5]John Riordan.Combinatorial Identities[M].NewYork:Roberte Krieger Publishine Company Huntington,1979.