低信噪比下的码速率估计算法研究

许 斌， 鲁茂昌， 秦文兵

(装备学院 北京 101416)

低信噪比下的码速率估计算法研究

许 斌， 鲁茂昌， 秦文兵

(装备学院 北京 101416)

经过理论推算与仿真得出，在二次小波变换后再进行循环累积量计算，可提高循环频率域的谱线峰值，提升算法在低信噪比下的估计精度。仿真结果表明，改进算法对码速率信息提取的信噪比要求降低了约3dB。

码速率估计； 小波变换； 循环累积量

引言

码元传输速率指单位时间内在信道中传送的码元数目，它是数字调制信号的一个关键参数。在电子对抗和非协作通信中，码速率估计是进行干扰的前提，同时也是信号盲识别和盲解调的重要依据。

文献[1]介绍了二次小波变换的码速率估计算法。文中指出，对信号进行二次小波变换后求其系数模值的傅里叶变换，通过寻找第一非零谱线所对应的频率即可获取码元速率。但仿真发现，在低信噪比下利用该算法进行码速率估计，存在谱线峰值不明显导致估计精度低的问题。

针对这一问题，本文做了改进，在求取信号的二次小波变换后引入循环累积量计算，在循环频率域完成码速率信息提取，第一非零频率处谱线峰值所对应的频率即为码元速率。仿真结果表明，利用改进算法进行码速率估计，谱线峰值得到了明显加强，低信噪比下的估计精度也有所提高。

1 信号二次小波变换的时域分析

信号的小波变换可定义为[2]

式中，a是伸缩因子，τ是平移因子，s(t)是信号，ψ(t)是母小波，ψa(t)是子小波。

因为Haar小波在信号细节检测方面具有良好的性能，故选择使用Haar小波作为母小波进行小波变换。

在一个码元周期内，信号的小波变换系数的模值为一个常数。通常伸缩因子远远小于码元周期，所以在码元的变化时刻，小波变换系数所产生的变化，可以认为是突变，即可以当作脉冲信号。为验证上述分析，针对2FSK信号，在无噪声情况下，做一次小波变换的实验仿真，结果示于图1。仿真条件：小波收缩因子a＝16，采样率fs＝1000Hz，载波频率fc＝20Hz，码速率R＝10Hz。

图1 2FSK信号的小波变换仿真

由图1可以看出，在一个码元区间内，信号的一次小波变换系数的模值为一个常数，且对于2FSK信号有两个恒定的常数值；在码元变换时刻出现了模值跳变，相比于码元周期，该跳变信号可看成是脉冲信号。

我们可以将一次小波变换系数的模值表示为如下形式

式(2)中，Ts为码元长度，Bn为单个码元小波变换后的包络，Cn为码元变化时刻的幅度，g(t)为矩形脉冲波形，δ(t)为脉冲信号。

将coef(t)再进行一次小波变换可以得到以下结果

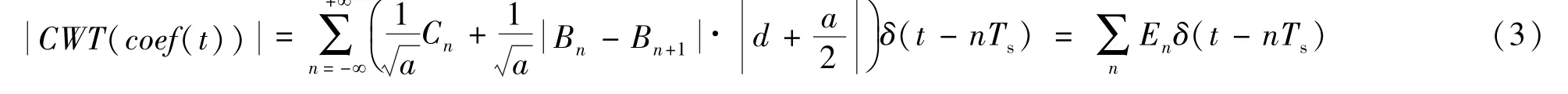
由式(3)可以得知，信号的二次小波变换系数模值是间隔为Ts的脉冲序列，从频域的角度分析，CWT(coef(t))应是间隔为m倍码速率的谱线，且第一个非零谱线所对应的频率或谱线间的最小间隔即为信号的码元速率[3]。

2 基于快速傅里叶变换的码速率提取

由上节分析可知，对信号二次小波变换后系数的模值直接进行傅里叶变换，第一个非零谱线所对应的频率即为信号的码速率。以2FSK信号为例，在不同的信噪比下求其二次小波变换，变换后结果的表达式如式(3)所示，频域分析结果示于图2。仿真条件：小波收缩因子a＝16，采样率fs＝1000Hz，载波频率fc＝20Hz，码速率R＝10Hz。

图2 二次小波变换的频谱图

由图2的仿真结果可以发现，在SNR＜3dB时，信号谱线几乎被噪声淹没。因为该算法通过识别谱线完成对信号的码速率估计，所以谱线与底噪的比值越大，估计精度越高。为了叙述方便，定义信噪峰值比为信号的第一个非零谱线值与最大噪声值之比。本文引入循环累积量计算提高低信噪比下的信噪峰值比。下节将主要介绍采用循环累积量法在循环频率域提取码速率信息的方法。

3 基于循环累积量的码速率提取

把二次小波变换后的数据CWT(coef(t))记为s(i)，i＝0，1，2…N－1，则其二阶样本循环矩为

其中，α为循环频率，τ为延时，T为数据长度。上式循环矩相当于将s(i)s(i＋τ)的频谱左移频率α后，再取时间平均[4]。因此，只要s(i)s(i＋τ)存在频率为α的谱线，则Mα2s≠0。

信号的二阶循环累积量为

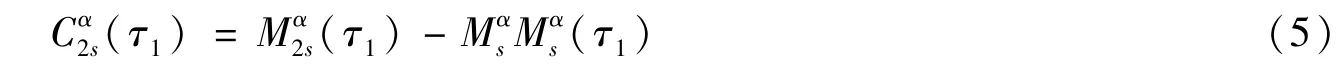
令τ1＝0，则上式为

因为二次小波变换后，在整数倍码速率处存在谱线，所以可以通过确定频率不为零的谱线的频率位置估计码速率。求CWT(coef(t))的二阶循环累积量则中第一个非零谱线峰值所对应的频率α，即为信号的码速率。

如第2节中仿真一样，以2FSK信号为例，在不同的信噪比下，使用循环累积量在循环频率域提取码速率信息，如图3所示。仿真条件：小波收缩因子a＝16，采样率fs＝1000Hz，载波频率fc＝20Hz，码速率R＝10Hz。

图3 不同信噪比下小波系数二阶循环累积量处理后的频谱图

由图3可以看到，在SNR≥0dB时，有明显的峰值存在，且峰值与噪声区分明显，较直接进行傅里叶变换有很大的改善。两种算法的信噪峰值比如图4所示(CUM为二阶循环累积量处理后的数据统计结果，FFT为傅里叶变换后的数据统计结果)。

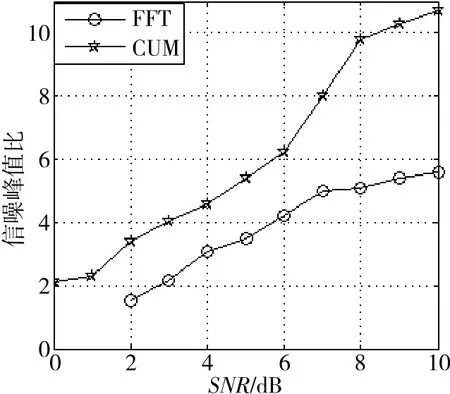
图4 不同信噪比下两种算法的信噪峰值比比较

由图4的仿真结果知道，采用二阶循环累积量处理后，信噪峰值比有了明显的改善，改进算法对信噪比的要求降低了约3dB。

根据仿真结果，选择调制信号循环累积量最大值的2/3作为阈值，在不同的信噪比下，在采样率fs＝1000Hz、载波频率fc＝20Hz、码元速率R＝10Hz的条件下，对每一种调制信号做100次的Monte Carlo仿真，统计估计结果的均值和方差，如表1所示。

表1 不同信噪比下码速率估计

由表1中的数据可以看到，当SNR≥5dB时，在仿真条件下，利用该算法能实现对各数字调制信号码速率的准确估计。由信噪比小于3dB时估计结果的均值和方差可以知道，虽然改进算法没能完全准确地实现码速率的估计，但其偏差较小，波动不大。

需要指出的是，应用高阶循环累积量进行码速率估计增加了算法计算量，降低了算法的实时性。这里以长度N＝1024的数据来说明算法改进前后计算量的变化。计算该段数据的频谱，所需的复数乘法数为在与傅里叶变换有相同的频率分辨率的情况下，计算该段数据的二阶循环累积量，不计数据幂次方等运算的影响，其所需的复数乘法数为524288。对比可以看出，改进后算法的计算量增加，复杂度增大。

4 结束语

仿真发现，利用二次小波变换在频率域进行码速率估计的方法，在信噪比SNR≤3dB时，码速率处谱线峰值几乎淹没在噪声中，影响了估计精度。为此，本文引入循环累积量计算，在循环频率域精确地完成了对信号的码速率估计。通过仿真对比发现，改进算法对信噪比的要求降低了约3dB。统计不同信噪比下100次Monte Carlo估计结果的均值和方差后知道，在信噪比SNR≥5dB时，改进算法可以实现对各数字调制信号码速率的准确估计，但循环累积量计算增加了算法的复杂度，降低了实时性。

[1] 罗华飞.小波域的数字调制信号识别及码速率估计[D].哈尔滨工程大学，2008.

[2] 杨福生.小波变换的工程分析与应用[M].北京：科学出版社，1999.

[3] 纪 勇，徐佩霞.基于小波变换的数字信号码速率估计[J].电路与系统学报，2003，8(1)：12～15.

[4] 张贤达，保 铮.非平稳信号分析与处理[M].北京：国防工业出版社，1998.

Research on Code Rate Estimation Algorithm at Low SNR

Xu Bin， Lu Maochang， Qin Wenbing

The theoretical calculations and simulations show that the spectral peak can be improved and the code rate estimation accuracy can be increased by combining cyclic cumulants with the secondary wavelet transform.The simulation results prove that the requirement of SNR for the code rate extraction reduces about 3dB with the improved algorithm.

Code rate estimation； Wavelet transform； Cyclic cumulant

TN914

A

CN11-1780(2014)02-0060-04

许 斌 1973年生，硕士研究生导师，主要研究方向是空间信号与信息处理。

2013-12-06 收修改稿日期：2013-12-17

鲁茂昌 1988年生，在读硕士研究生，主要研究方向是无线信号处理。

秦文兵 1978年生，博士，信号盲处理重点实验室工程师，主要研究CDMA，OFDM等高速宽带信号处理技术。