基于滤波对角化方法提升傅里叶变换质谱数据质量

方剑委，张纪阳，徐长明，张 伟，刘 伟，谢红卫

(国防科学技术大学机电工程与自动化学院自动控制系，湖南 长沙 410073)

基于滤波对角化方法提升傅里叶变换质谱数据质量

方剑委，张纪阳，徐长明，张 伟，刘 伟，谢红卫

(国防科学技术大学机电工程与自动化学院自动控制系，湖南 长沙 410073)

傅里叶变换质谱仪能够达到很高的分辨率，在分子生物研究中得到广泛应用。数据处理方法，特别是底层信号的处理，对于提升数据质量至关重要。滤波对角化(filter diagonalization method，FDM)相比传统的快速傅里叶变换算法(fast Fourier transform method，FFT)，能进一步提高图谱分辨率、降低信号强度测量误差。本工作通过仿真以及实际质谱数据分析，证明了相对FFT而言，FDM可将图谱的分辨率提高1个数量级左右，并且可以有效降低信号强度测量误差。另外，还研究了算法参数优化问题，为算法应用推广提供了参考。

傅里叶变换质谱仪；分辨率；滤波对角化；快速傅里叶变换算法；参数优化

质谱仪的性能指标主要有灵敏度、信噪比、质量精度、质量范围以及分辨率等[1]。其中，分辨率决定着图谱中大量存在的同位素峰能否明显区分出来，对精确解析图谱起着至关重要的作用[2]。现代质谱仪一般都具有高通量、高灵敏度和高分辨率的特点，在生命科学等研究领域中发挥着重要作用[3-4]。就目前亟待发展的自顶向下(Top-Down)分析技术来说，分析对象为整体蛋白质，分子质量比较大(根据Swiss-Prot数据库统计，人类蛋白质的分子质量集中在10～100 ku之间)，带电荷较多，其同位素峰分布更加复杂，对仪器分辨率的要求更高。因此，对目前的质谱分析来说，提高仪器分辨率和质谱数据质量是一个需要长期努力的任务。

目前，傅里叶变换质谱仪(Fourier transform mass spectrometry，FTMS)[5]的分辨率已经突破百万，能够用于分析带有几十个电荷的蛋白质序列[6]。但在高通量的实验中，分辨率会受到分析时间、噪声、信号抑制等因素的影响，不是所有的图谱信号都能达到最高的分辨率。而且，由于需要综合考虑多方面的性能，并且提供稳定可靠的分析结果，商业化质谱仪的分辨率一般不能达到106。例如，热电公司的新型LTQ-Orbitrap Elite是一种傅里叶变换质谱仪，其标称分辨率为240 000，但是在常规分析中，为了兼顾图谱产出数量，设定分辨率一般只有30 000～50 000。另外，同一张图谱中，不同信号强度的谱峰分辨率也不同。信号强度较强的谱峰会有较高分辨率，一般能够达到仪器设定的最高分辨率；而信号强度较低的谱峰，分辨率会有显著降低。有研究表明，傅里叶变换质谱仪的数据采集和处理方式会影响仪器实际解析出的分辨率[7-8]。例如，LTQ-Orbitrap Elite采用了增强型傅里叶变换(eFT)，在不增加硬件能力的情况下，能够将图谱分辨率提高至原来的2倍[9]。在复杂噪声干扰的情况下，基于快速傅里叶变换算法得到的质荷比和信号强度可能并非最优结果，这有望通过优化算法得到进一步提升，例如，本工作拟研究的滤波对角化(filter diagonalization method, FDM)方法[10]。特别强调的是，高性能的傅里叶变换质谱仪虽然在质荷比测量上的精度很高(相对误差可以小于10-6)[4]，但在信号测量精度上还存在误差较大的问题[11]，这主要是高通量和高复杂度样本分析带来的挑战，需要在数据处理方法和硬件改进上加以努力。

目前，虽然已有团队将FDM用于傅里叶变换质谱仪的数据处理，显著提高了图谱的分辨率，降低了同位素峰分布引起的解析误差，但该方法还仅在特定的设计实验中进行了验证，尚未大规模使用，还有很多应用中的细节问题尚不明确。本工作利用仿真以及实际质谱数据验证FDM算法的性能，研究算法参数优化问题，为该算法的应用提供参考。

1 材料和方法

1.1数据来源

采用了两类数据来研究FDM算法的性能。

一是MATLAB仿真数据，即利用设定的几组频率、幅值和相位等信息构造相应的正弦函数并相互叠加，得到时域信号，示于公式(1)。

(1)

其中，t为时间，Fi为设定频率，φi为设定相位，Ii为信号强度(即正余弦信号的幅值)。

二是傅里叶变换质谱图谱数据。大规模蛋白质组分分析中产出的质谱数据，一般都是经过快速傅里叶变换算法(FFT)变换处理后的图谱，时域信号(即电压信号)很难获取。

本工作利用图谱构造其时域信号，即利用实验获得的质荷比和信号强度来得到公式(1)中的频率和幅值。质荷比转换频率数据是根据仪器获取数据的原理来计算的[12]，示于公式(2)。

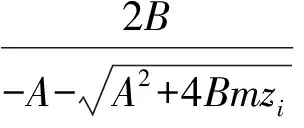
(2)

其中，A、B为实验设备参数，可调整F之间间隔大小，从实验数据文件中获取。数据分析表明，F线性递增，说明数据采集的等间距性，为软件的参数设置提供了依据。这里，着重强调相位φ，由于现在质谱仪多采用相位同步技术，故相位一致，可设置为0。当然，在仿真分析中，可以采用随机相位。

本工作采用的实验数据来自美国系统生物学研究所(Institute for Systems Biology,ISB)2008年发布的标准蛋白质数据集[13]，数据采用了第3次实验中傅里叶变换质谱仪产出的“B06-11080.RAW”质谱数据作为分析对象。

1.2FDM算法

FDM是解析图谱的参数匹配法。它由Neuhauser[14]于1991年提出并用于量子力学计算。Mandelshatam等[15]将其应用于时间信号处理。现主要用于核磁共振信号处理，并取得了良好的效果[16]。FDM算法的功能与傅里叶变换算法一样，即求取时间信号的频率、幅值、相位等信息。

一般来说，离散数字信号可表示为：

(3)

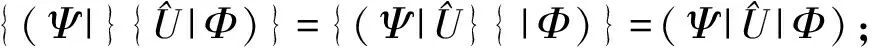
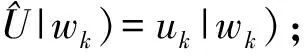
其中，符号|*)和(*|分别表示左右矢量。依上述性质计算，可得特征值uk=e-itwk。cn亦可写成：

(4)

1)滤波过程。用酉算子构建一组基向量，即为：

(5)

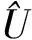
(6)

其中，Bk为列向量，[Bk]n为基向量|n)的线性组合系数[17]。理论上可以证明，当该基向量的秩为M=N/2时，求解唯一[18]。其中，N为样本总数。显然，此组基向量受限于N值，即N值越大，数据处理难度越大。然而，FDM可以很好地解决此缺陷。它将基向量|0),|1),…，|n)傅里叶变换为傅里叶基向量|φj)，公式为：

(7)

此变换一一对应。根据谱分解公式，公式(7)可写为：

(8)

可以看出，每一傅里叶基向量都唯一对应着一段频率范围，即|φj)→[wmin，wmax]。也就是说，要解某一个特征向量|wk)，只需用其相应的傅里叶基向量线性组合即可[18]，即：

(9)

那么，这就很好地解决了基向量受限于数据点个数的问题。其实，此过程类似于窗口技术[19]，即滤掉不起作用的基向量，保留有用的基向量，从而求得特征向量及其特征值。这样做的好处是，降低数据计算量，提高图谱计算效率，故称为滤波。

U1Bk=uU0Bk

(10)

(11)

故可求得ck(k=0，1，…)值。根据公式uk=e-itwk可得频率wk。比较公式(3)、(4)，可知dk=(0|wk)2。根据公式(9)，可得：

(12)

1.3软件工具

Mandelshtam等[21-22]实现了完整的FDM算法，运行于Linux系统上，可以通过Cygwin来实现Windows下的安装和使用。安装软件Harminv有以下3个步骤：1)需安装Windows系统下的Linux虚拟环境Cygwin；2)在此基础上，安装好基础线性代数子程序包BLAS、线性代数安装包LAPACK及gfortran编译器，这是相关矩阵运算所必须的；3)根据电脑配置，设置路径环境变量并完成编译。安装成功后，按格式“harminv 参数设置 < input.dat”输入命令，即可完成数据处理。“input.dat”为输入信号，中间为相关参数设置，主要参数列于表1。

表1 软件Harminv的参数设置

Harminv可计算输出频率(frequency)、衰减因子(decay constant)、质量因子(Q)、幅值(amplitude)、相位(phase)和错误率(error)等。其中，1/Q表示谱峰半峰高处的峰宽，可以用于计算分辨率。

2 结果与讨论

2.1MATLAB仿真数据

假定相位φk为0，输入信号由下式得出：

(13)

其中，fk为第k个频率值，Ak为相应幅值，k为频率点个数，t为时间。t=1/fs，2/fs，3/fs…，N/fs，可知信号长度是由数据点N和采样频率fs决定的。

首先，给定f={12,12.1,12.2}，A={1}，且fs=100，两种算法的检测结果示于图1，相关数据列于表2。FFT算法的信号强度测量误差百分比按公式((实测幅值-理论幅值)/理论幅值)×100%计算。计算得出，当数据点N为524、2 048、65 536时，误差分别为16.41%、9.04%、5.61%。需要说明的是，出于计算上的考虑，FFT和FDM得到的频率都是关于原点对称的，这将会导致信号幅值分配在对称位置上，得到的信号强度为原来的一半。

从上述检测结果，可得出两个结论：一是同一信号长度下(即N=524)，FDM检测结果优于FFT，具体体现在FDM准确测出所有频率点且信号强度测量误差仅为0.096%(如表3)，但是FFT测得的频率点混淆在一起，且信号强度测量误差达到16.41%；二是N增大时，FFT频率点检测效果有较大提升，信号强度测量误差也随之减少至5.61%，但要达到与FDM相同结果，需要很大的数据量。

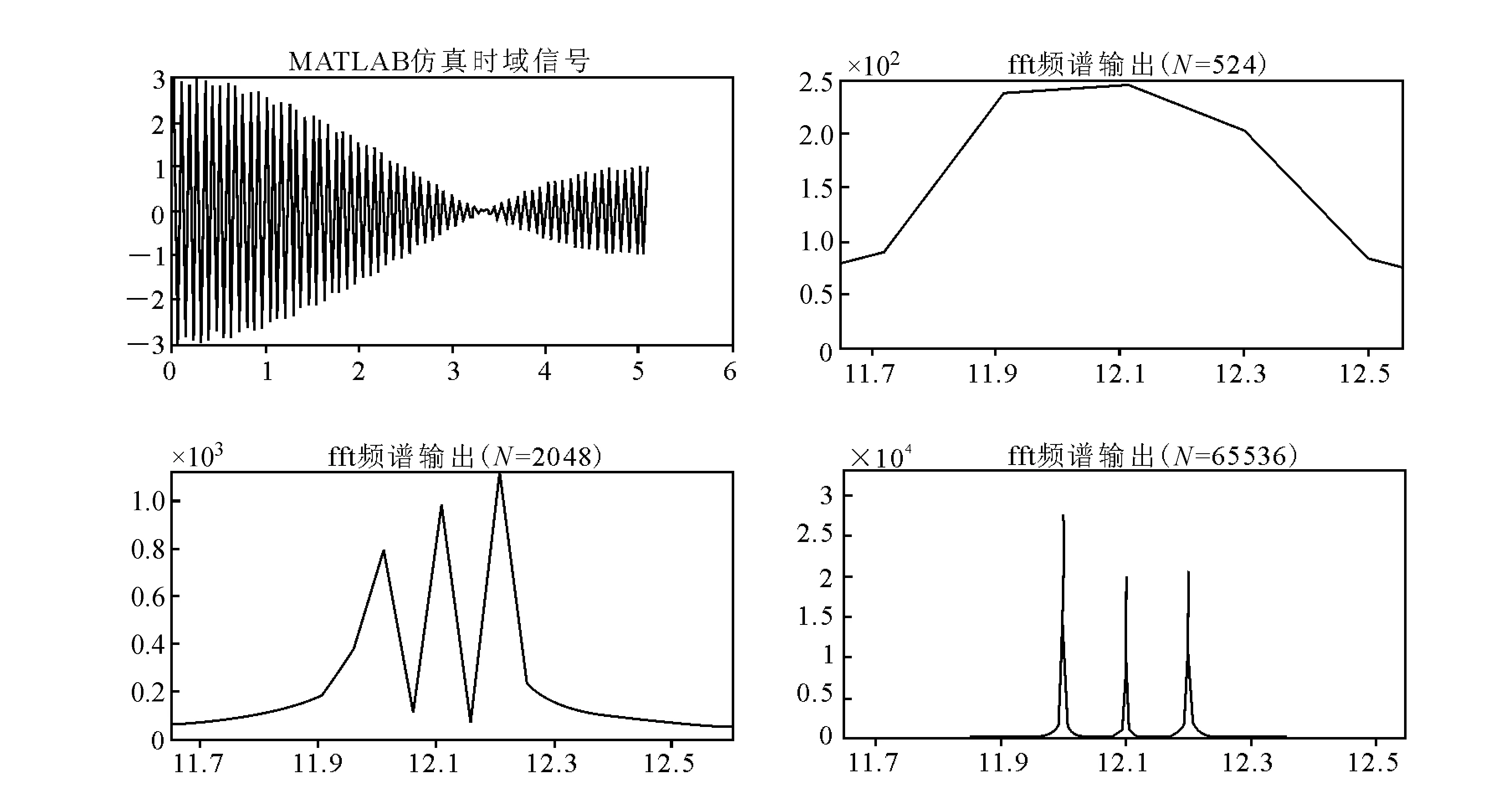
图1 不同N值下，FFT的检测结果Fig.1 The test results of the algorithm FFT in different data points

表2 N=524时，FDM算法的检测结果

注：*错误率表示检测结果的可靠性，其值越小结果越可靠

2.2实际质谱数据

2.2.1单组数据分析 任选一张图谱作为实验对象，质荷比范围300～1 600，信号强度范围190～17 564，其中信号强度不为0的数据点176个。将其按上述步骤转换成时域信号，作为两种算法的输入信号，结果列于表3。在构造中，选择图谱的平均采样数据点数目N=4 000，平均采集时间1 s，作为产生时域信号的采样参数。

表3 FFT、FDM的检测结果

注：*分辨率计算公式为R=M/DM(M为两峰的平均质量，DM为两峰之间的质量距离)

从表3可得出结论：在分辨率方面，FDM比FFT增加了1～2个数量级；在信号强度测量误差方面，FDM比FFT精确了3个数量级左右；总之，FDM检测效果优于FFT。FDM检测效果较好的原因：一是其本身算法的优越性；二是所设定的输入信号无噪声影响。

2.2.2多组质谱数据分析验证 为验证结论的可靠性，将文件“B06-11080.RAW”中的6 556张质谱图数据进行统计分析，得到的分辨率及信号强度测量误差的箱线图对比结果示于图2，数据结果列于表4和表5。图2的横坐标表示所要对比数据的来源，纵坐标表示分辨率(或信号强度测量误差)数据的箱线结果。其中，采用图谱的平均分辨率作为分辨率的评价指标，采用平均信号强度误差作为信号强度测量误差的评价指标。

从图2和表4、5可得出结论：一是在分辨率方面，FDM>原图分辨率>FFT，其中，FFT与原图分辨率基本处于同一数量级，FDM则增加了1～2个数量级；二是在信号强度测量误差方面，FDM比FFT精确了3个数量级左右，验证了上述结论。

2.2.3参数优化 首先，考虑数据量N和采样频率fs的作用，它们决定信号长度，取值满足一定条件，即可得与原图谱相同的信号长度。

图2 两种算法的分辨率、信号强度测量误差的箱式分布图Fig.2 The box plot of the resolution and the measured signal intensity error of the algorithm FDM and FFT

表4 两种算法的分辨率对比

其次，考虑质荷比m/z与频率数据F之间的转换常数K。由于Fk和Fk-n(n=1, 2，…)的间隔过大(或过小)会影响结果，所以有必要调节K值。通过简单分析和实际测试，发现间隔控制在1～10效果最佳，但在后续数据处理中要注意变换回去，以确保数据处理的准确性。

表5 两种算法的信号强度测量误差对比Table 5 The measured signal intensity error of the algorithm FDM and FFT

再者，考虑软件Harminv相关参数并考察其局限性。比如，增加参数d值时，基函数的数目随之增加，亦可改善结果；但其值过大会增加矩阵维数，从而影响准确度，通常基函数的个数不超过300。其局限性为：检测频率点总数与基向量个数相关，通过简单分析和实际测试，发现可检测的频率点总数不超过300；灵敏度不高，检测结果易受幅值大小的影响。

3 结论

本工作分别从仿真数据和实际质谱数据入手，验证了FDM算法的性能，体现在进一步提高了图谱分辨率、降低了测量信号强度误差等，为傅里叶变换质谱仪的后期数据处理提供了更为有效的方法；同时，研究了算法参数优化问题，为算法应用提供了参考。由于未能获得傅里叶变换之前的电压信号，在此采用了仿真、时频转换等方法进行算法的验证分析。

[1] DOMON B, AEBERSOLD R. Mass spectrometry and protein analysis[J]. Science, 2006, 312(5 771): 212-217.

[2] MCLAFFERTY F W. High-resolution tandem FT mass spectrometry above 10 kDa[J]. Accounts of Chemical Research, 1994,27(11): 379-386.

[3] JOHN R, YATES I I I. A century of mass spectrometry: From atoms to proteomes[J]. Nat Meth, 2011, 8(8): 633-637.

[4] NILSSON T, MANN M, AEBERSOLD R, et al. Mass spectrometry in high-throughput proteomics: Ready for the big time[J]. Nat Methods, 2010, 7(9): 681-685.

[5] SCIGELOVA M, HORNSHAW M, GIANNAK- OPULOS A, et al. Fourier transform mass spectrometry[J]. Mol Cell Proteomics. 2011, 10(7): M111.009431-1-19.

[6] MCLAFFERTY F W, FRIDRIKSSON E K, HO- RN D M, et al. Biomolecule mass spectrometry[J]. Science, 1999, 284(5 418): 1 289-1 290.

[7] QI Y, BARROW M P, LI H, et al. Absorption-mode: The next generation of Fourier transform mass spectra[J]. Anal Chem, 2012, 84(6): 2 923-2 929.

[8] XIAN F, HENDRICKSON C L, BLAKNEY G T, et al. Automated broadband phase correction of fourier transform ion cyclotron resonance mass spectra[J]. Anal Chem, 2010, 82 (21): 8 807-8 812.

[9] MICHALSKI A, DAMOC E, LANGE O, et al. Ultr-high resolution linear ion trap Orbitrap mass spectrometer (Orbitrap Elite) facilitates top down LC-MS/MS and versatile peptide fragmentation modes[J]. Mol Cell Proteomics, 2012, 11(3): O111.013698.

[10] KOZHINOV A N, TSYBIN Y O. Filter diagonalization method-based mass spectrometry for molecular and macromolecular structure analysis[J]. Anal Chem, 2012, 84(6): 2 850-2 856.

[11] MILADINOVIC S M, KOZHINOV A N, GORSHKOV M V, et al. On the utility of isotopic fine structure mass spectrometry in protein identification[J]. Anal Chem, 2012, 84 (9): 4 042-4 051.

[12] JONATHAN AMSTER J. Fourier transform mass spectrometry [J]. Journal of Mass Spectrometry, 1996, 31(12): 1 325-1 337.

[13] KLIMEK J, EDDES J S, HOHMANN L,et al. The standard protein mix database: A diverse data set to assist in the production of improved peptide and protein identification software tools[J]. J Proteome Res, 2008, 7(1): 96-103.

[14] NEUHAUSER D J. Time-dependent reactive sc- attering in the presence of narrow resonances:Avoiding long propagation times[J]. J Chem Phys, 1991, 95(7): 4 927-4 932.

[15] MANDELSHTAM V A, TAYLOR H S. A low-storage filter diagonalization method for quantum eigenenergy calculation or for spectral analysis of time signals[J]. J Chem Phys, 1997, 106(12): 5 085-5 090.

[16] HU H, VAN Q N, MANDELSHTAM V A, et al. Reference deconvolution, phase correction, and line listing of nmr spectra by the 1d filter diagonalization method[J]. Journal of Magnetic Resonance, 1998, 134(1): 76-87.

[17] WALL M R, NEUHAUSER D. Extraction th- rough filter-diagonalization of general quantum eigenvalues or classical normal mode frequencies from a small number of residues or a short-time segment of a signal[J]. J Chem Phys, 1995, 102 (20):8 011-8 022.

[18] MANDELSHTAM V A. FDM: The filter diagonalization method for data processing in NMR experiments[J]. Progress in Nuclear Magnetic Resonance Spectroscopy, 2001, 38(2):159-196.

[19] MIZUSAKI T, KANEKO K, HONMA M, et al. Filter diagonalization:A new method for large-scale shell-model calculations[J]. Acta Physica Polonica B， 2011, 42(3/4): 447-450.

[20] BARINOVS G, NYMAN G. On the resolution of the filter diagonalization method[J]. Chemical Physics, 2002, 281(1): 23-31.

[21] MANDELSHTAM V A, TAYLOR H S. Harmonic inversion of time signals and its applications[J]. J Chem Phys, 1997, 107(17): 6 756-6 769.

[22] MANDELSHTAM V A. On harmonic inversion of cross-correlation functions by the filter diagonalization method[J]. Journal of Theoretical and Computational Chemistry, 2003, 2(4): 1-9.

2014年第二届原位电离质谱会议(AIMS2014)通知

由中国质谱学会主办、华质泰科公司承办的“2014年第二届原位电离质谱会议”(AIMS2014)将于2014年4月1～4日在湖南张家界举办。我们诚挚的邀请您作为特邀参会嘉宾，莅临这一盛会，与同仁共享新理念，研讨新热点，交流新经验，推动实时科学与质谱行业的整体发展。

在国民经济、文化发展与百姓生活日新月异的今天，食品安全及环境污染问题愈演愈烈，塑化剂风波、三聚氰胺及双聚氰胺非法添加、瘦肉精滥用等兽药农药残留超标、各地持续大面积雾霾凸现等频发突发事件一直成为全民议论的焦点，分析监测行业承载着前所未有的压力。如何快速、高效、准确和灵敏地检测并有效地控制有毒、有害物质日渐成为了科学检测队伍所面临的难题。原位电离质谱技术自2009年前后正式引入中国，至今已有3年多的历史。在一大批知名学者所领导的学术团队和推广公司的热情倡导与大力推动之下，中国原位电离质谱技术的研发与应用也紧随国际航标，在实践中快速发展，优化行业合作，创新与应用相结合，并在诸多领域率先实现瓶颈突破，取得了非常可喜的阶段式成果。

如果说2013年是原位电离质谱技术的发展和实时直接分析技术的应用突飞猛进的一年，那么2014年就是中国原位电离质谱技术持续扩大影响和稳步走向国际社会的一年，为响应这一发展态势，在张家界举办的第二届中国原位电离质谱会议(AIMS2014)将集结全国各行业的分析测试精英，延续并进一步深化原位电离技术带来的革命性影响。欢迎质谱工作者和相关专业的学者积极参与！

如您希望参加本次会议，或者对本次会议感兴趣并想进一步了解细节，请邮件联系组委会。欢迎企业赞助本次会议，欲了解详细信息，请联系组委会。

联系人：王争

电话：+86-10-6439-9978 转0;传真: +86-10-6439-9499

电子信箱：aims@aspectechnologies.com

2014年中国原位电离质谱会议(AIMS2014) 组委会

2013年12月20日

EnhancetheQualityofFourierTransformMassSpectrometryDataBasedontheFilterDiagonalizationMethod

FANG Jian-wei, ZHANG Ji-yang, XU Chang-ming, ZHANG Wei, LIU Wei, XIE Hong-wei

(DepartmentofAutomaticControl,CollegeofMechanical&ElectronicEngineeringandAutomation,NationalUniversityofDefenseTechnology,Changsha410073,China)

Fourier transform mass spectrometry (FTMS) is capable of achieving very high resolution, which is widely used in molecular biological research. Data processing method, especially at the signal level, is crucial for improving the quality of the data. Compared to fast Fourier transform method (FFT), filter diagonalization method (FDM) can improve the resolution of the mass spectra and reduce the measured signal intensity error. In this work, the performance of FDM was investigated using the simulation data and experimental mass spectrometry data. Comparing to FFT, FDM was improved the resolution of the mass spectra by a factor of one order and reduced the measured signal error effectively in experimental mass spectrometry data. Meanwhile, this work also investigated the parameter optimization problem that could be a reference for the application of FDM.

fourier transform mass spectrometer; resolution; filter diagonalization method; fast Fourier transform method; parameter optimization

2013-05-13；

：2013-06-30

国家自然科学基金(31171266,31000587,31000591)资助

方剑委(1989～)，男，福建莆田人，硕士研究生，生物信息学专业。E-mail: fangjianwei0705@sina.com

谢红卫(1965～)，男，湖北洪湖人，教授，从事生物信息学和可靠性分析研究。E-mail: xhwei65@163.com

时间：2013-11-22；

：：http://www.cnki.net/kcms/detail/11.2979.TH.20131122.1119.001.html

O 657.63

：A

：1004-2997(2014)01-0001-07

10.7538/zpxb.youxian.2013.34.0007