正负折射率含缺陷1维光子晶体多通道滤波器

熊翠秀，蒋练军，王景艳

(1.湖南城市学院通信与电子工程学院，益阳413000;2.保山学院数学学院，保山678000)

引 言

光子晶体是指介质的折射率或介电常数按周期性变化的人工材料，其概念最早于1987年分别由YABLONOVITCH和JOHN提出［1-2］。由于材料的周期性从而出现光子带隙。当周期性结构中引入缺陷时会在光子带隙内产生缺陷模。由于光子晶体的光学传输特性具有很好的可调性，因此光子晶体在各方面有很好的应用潜力。

随着通信技术的发展，信息密集程度越来越高，光子晶体的出现正好迎合了多信道传输的要求。基于此，不同的研究者设计并研究了具有不同特性、适用于不同场合的光子晶体滤波器。如利用缺陷产生缺陷模［3-5］、异质结产生缺陷模［6-7］、量子阱产生缺陷模［8-10］、普通介质无缺陷1维光子晶体的全反射隧穿效应产生缺陷模［11-13］及基于实数折射率和复折射率介质交替排列的多通道倍频滤波［14］等。为了增加信道传输数，对于利用缺陷产生缺陷模的光子晶体滤波器，可以通过增大高低折射率之差［15］和用正负折射率材料交替排列［16］两种方式来增大禁带的宽度。本文中利用第2种方法，即用正负折射率交替排列的办法增大禁带的宽度，采用参考文献［3］中提出的1维光子晶体模型B(AB)m(ACB)n(AB)mB，利用传输矩阵法［17］通过MATLAB编程计算了该模型的透射谱。为了与参考文献［3］中的研究结果进行比较，仅仅把B介质由原来的正折射率介质变为负折射率材料，而保持其它参量不变。研究结果显示，该结构在正负折射率材料交替排列时表现出很特别的多通道滤波特性。最后结合光的波动理论分析了这种多通道滤波产生的机理。

1 理论模型和结构参量

正负交替1维光子晶体参照参考文献［3］中的模型B(AB)m(ACB)n(AB)mB，其具体结构如图1所示。其中A与B是基元介质，且B介质为负折射材料，而C介质为缺陷。不考虑色散和吸收，m和n为基本单元(AB)和(ACB)的重复周期数。为了与正折射率介质的多通道滤波器的特性进行比较，除了把B介质的折射率取负值外，其它参量与参考文献［3］中的一致，即A、B和C介质层的折射率分别取 nA=2.6，nB=-1.45，nC=1.8，相对磁导率分别为μA=μC=1，μB=-1。光学厚度分别取 nAdA=λ0/4，nBdB=-λ0/4，nCdC=k× (λ0/4)，其中 dA，dB和dC分别是介质A，B和C层的几何厚度，λ0为中心波长，k取正整数。

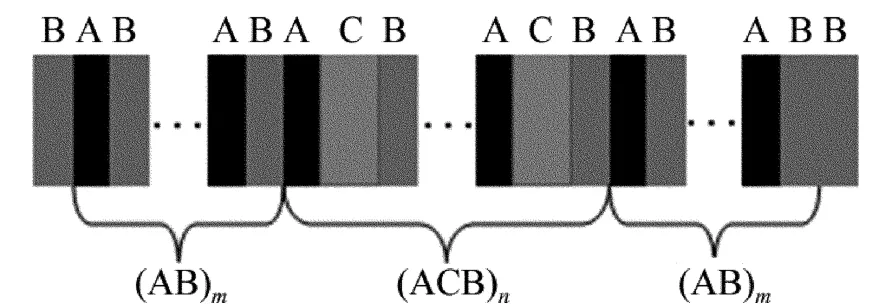
Fig.1 Structure of1-D photonic crystal B(AB)m(ACB)n(AB)m B

根据薄膜光学理论，波长为λ的光在每层介质中的传输特性可以用一个2×2的传输矩阵表示表示，对于第 j层，其传输矩阵［17］为:

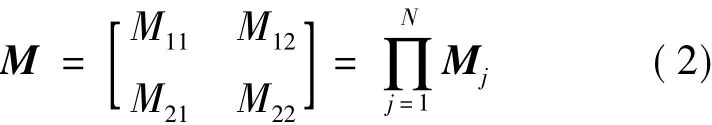
式中，N是总的介质层数。光从空气入射到光子晶体时的反射系数表如下:

2 数值计算结果

用传输矩阵法［17］计算该1维光子晶体在不同结构参量下的透射谱。在MATLAB环境下编程计算，计算过程中光场频率ω对中心频率ω0进行归一化，表示为ω/ω0，归一化频率的步长取0.000005。

2.1 (ACB)n的周期数n对缺陷模的影响

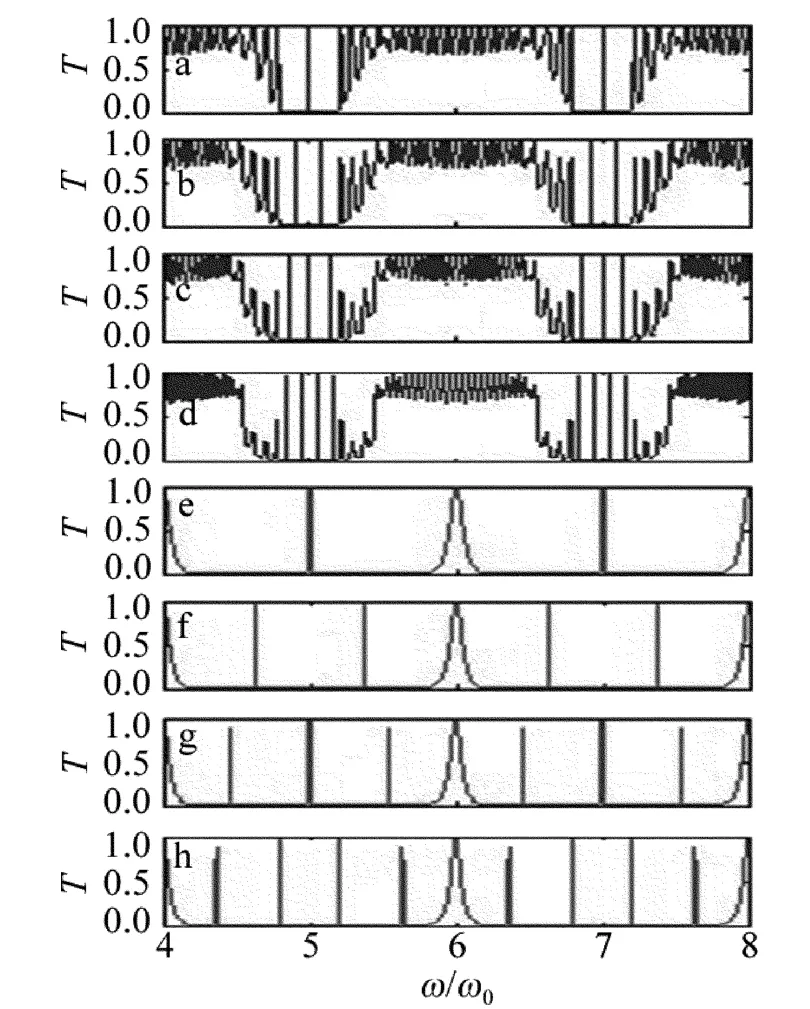
Fig.2 Transmission spectrum of B(AB)8(ACB)n(AB)8 B 1-D photonic crystalwhen n increasing

固定基本单元(AB)m的周期数m=8，介质C层的光学厚度取 nC×dC=1×(λ0/4)，即 k=1。(ACB)n的重复周期数n从1～4增大。其它参量不变，分别取nB=1.45和nB=-1.45，计算了正入射时1维光子晶体B(AB)8(ACB)n(AB)8B的透射谱，如图2所示。由图2可知:(1)在ω/ω0的奇数倍附近都出现了以ω/ω0的奇数倍为中心的禁带，但nB=-1.45和nB=1.45对应的透射谱明显不同，正负折射率交替排列1维光子晶体的每个禁带都以两侧ω/ω0的偶数倍为界，禁带宽度明显比正折射率交替排列1维光子晶体的禁带宽得多;(2)无论是正折射率材料交替排列，还是正负折射率材料交替排列，模型B(AB)m(ACB)n(AB)mB的1维光子晶体在本文中所取参量下，每个禁带内都有与(ACB)n重复周期数对应的n条透射峰，这n条透射峰关于禁带中心对称，随着(ACB)n重复周期数n的增大，各透射峰间的距离逐渐减小，这一现象与参考文献［3］中的结果一致，参考文献［3］中对上述现象产生的原因进行了详细的解释。

2.2 介质C层的光学厚度对缺陷模的影响

首先固定1维光子晶体B(AB)m(ACB)n(AB)mB的重复周期数为m=8，n=1。C层介质的光学厚度nCdC从1×(λ0/4)增加到4×(λ0/4)，分别取 nB=1.45和 nB=-1.45，计算正入射时，光子晶体B(AB)8(ACB)n(AB)8B的透射谱如图3所示。由图3可知:(1)nB=1.45时，C层介质的光学厚度分别为(λ0/4)的奇数倍和偶数倍时，禁带内分别出现了1条和2条透射峰，这与参考文献［3］中的报道一致;(2)当nB=-1.45时，且C层介质的光学厚度用k×(λ0/4)，禁带内出现了k条透射峰，这现象与nB=1.45的情况明显不同。

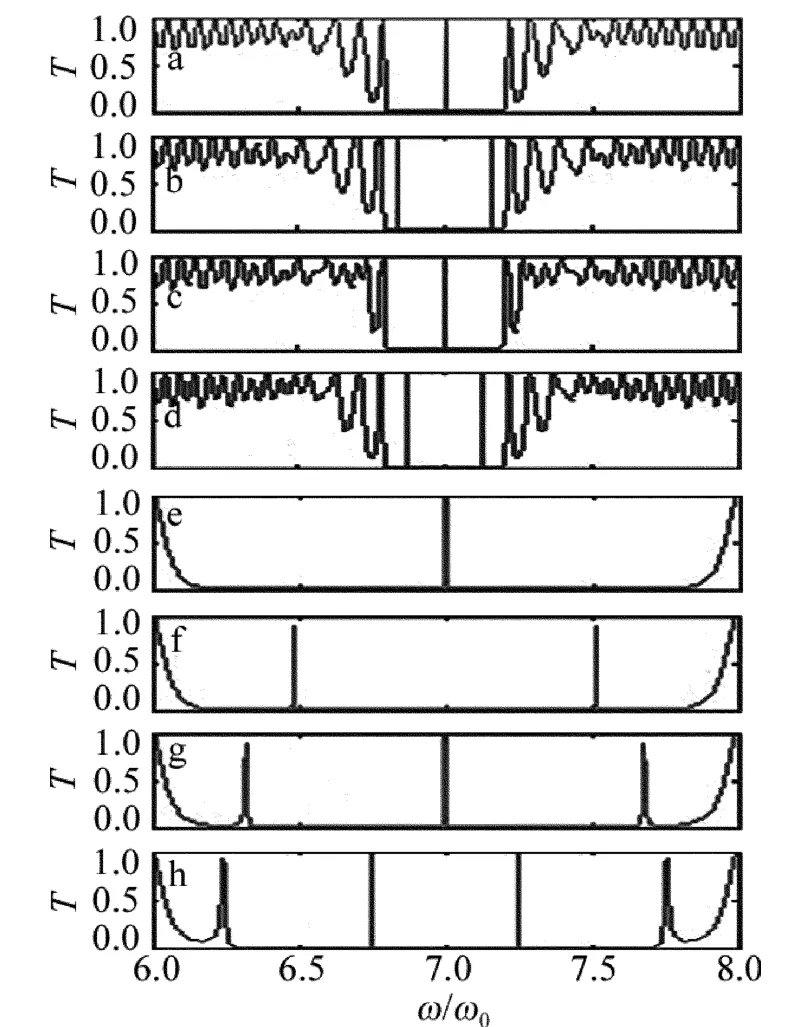
Fig.3 Transmission spectrum of B(AB)8(ACB)1(AB)8 B 1-D photonic crystalwhen the optical thickness ofmedium C increasing a—nB=1.45，k=1 b—nB=1.45，k=2 c—nB=1.45，k=3 d—nB=1.45，k=4 e—nB=-1.45，k=1 f—nB=-1.45，k=2 g—nB=-1.45，k=3 h—nB=-1.45，k=4

为进一步说明问题，在其它参量不变的情况下，图4中给出了正入射、且 nB=-1.45，m=8，n=4时，C层介质的光学厚度nCdC从1×(λ0/4)增加到6×(λ0/4)的透射谱。由图4可以看出，分别取k=1，2，3，4，5，6 时，禁带内分别有 4 × 1，4 × 2，4 × 3，4×4，4×5，4×6条透射峰，正好都有相应的 n×k条透射峰。结合图3e、图3f、图3g、图3h和图4可知，在所选的模型中，当介质A，B和C分别为正、负和正折射率材料，且各介质层的光学厚度满足nAdA=时，每个禁带内有n×k条透射峰，这些缺陷模以k组的形式出现，每组都有n条透射峰，总的缺陷模数有n×k条。

Fig.4 Transmission spectrum of B(AB)8(ACB)4(AB)8 B 1-D photonic crystalwhen the optical thickness ofmedium C increasing a—n=4，k=1 b—n=4，k=3 c—n=4，k=5 d—n=4，k=2 e—n=4，k=4 f—n=4，k=6

由上述现象可知，对于正负折射率介质交替排列的1维光子晶体B(AB)m(ACB)n(AB)mB，可通过调整(ACB)n的重复周期数n和C层介质的光学厚度nCdC，使禁带内出现所需的n×k条透射峰。与相同结构的正折射率材料交替排列的光子晶体相比，当n=1，且nCdC分别为λ0/4的奇数倍和偶数倍时，通道数分别增大为原来的k倍和k/2倍，信道容纳能力得到很大的提高。

3 多滤波通道形成的原因

为了明确多滤波通道形成的原因，以下从理论上分析滤波通道形成的机理。

该结构相当于在正和负折射率介质A和B周期性排列的结构中插入了n块介质C，介质C充当了缺陷，光子禁带中会出现光场局域，导致在缺陷处由于共振隧穿，产生缺陷模［3］，由于有n个缺陷，故有与n对应的n套缺陷模。当C层介质的光学厚度nCdC正好等于λ0/4时，正好有n条缺陷模。

对于两端的周期结构来说，一块缺陷介质C相当于就是一个法布里-珀罗微腔［18-19］，入射波在微腔内作往返反射和透射，以相同入射角θ入射过来的光线平行透射出去，由于多光束干涉可以得到干涉图样。本文中所取参量满足，则相邻两束出射光的光程差为:

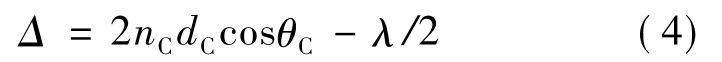
式中，θC是C层介质内光线与法线之间的夹角。

当复色光平行入射时，由于多光束干涉，只有在某些特定的频率附近出现了光强的极大值［20］，即亮条纹，也就是缺陷模，这些光强极大值对应的相邻两光束的光程差满足:

式中，j取整数。相应的角频率ωj和角频率间隔Δω分别满足:

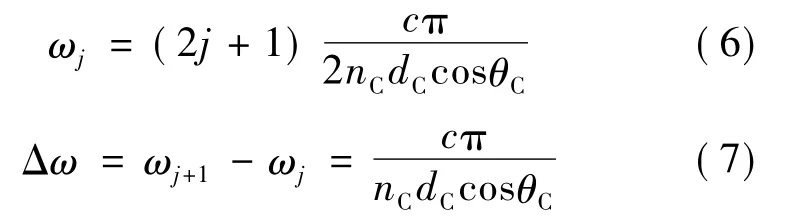
式中，c是真空中的光速。由此可见，每个缺陷形成一系列等频率间距的缺陷模。由(7)式可知，当缺陷介质C层的光学厚度增大时，相邻缺陷模的角频率间隔将减小，同一个禁带内容纳得下更多的缺陷模，相当于缺陷模分裂。为了结合前面的数值计算结果，以下仅考虑正入射情况。

(1)当 n=1，nCdC=1 ×(λ0/4)，且光束正入射时，由(7)式可知，缺陷模的归一化角频率和相邻缺陷模的归一化角频率间隔分别为:

(2)当 n=1，即 nCdC=k× (λ0/4)，且正入射时，由(7)式可知，相邻缺陷模的归一化角频率间隔变为:

而根据图2可知，在本文中所取的模型和结构参量下，当nB=-1.45时，每个禁带的归一化角频率宽度正好为2，因此只含一个缺陷层C时，每个禁带都容纳得下k个缺陷模，这与图3e、图3f、图3g和图3h一致。

(3)当n≥2，nCdC=1 ×(λ0/4)，且正入射时，每个禁带内每个缺陷块C产生一个缺陷模，因此每个禁带内有n个缺陷模;而nCdC=k×(λ0/4)时，每个缺陷模分裂为k条，故每个禁带内会出现n×k条缺陷模，于是出现了图4中每个禁带内有k组透射峰，每组透射峰由n条缺陷模组成的现象。

值得注意的是，根据上述分析可知，每个缺陷层在禁带内的缺陷模应以等间距出现，但图4中的每个禁带内，同一组透射峰的间距基本相等，而相邻两组间相邻的透射峰间距明显不等于同一组的间距。这是因为，缺陷个数为n，每个缺陷都产生k个缺陷模，因此每个缺陷对应的缺陷模在k组透射峰的每组里有1条，故相邻缺陷模间的角频率间隔应指相邻两组透射峰对应缺陷模间的角频率间隔。那么，缺陷模等间距应指相邻两组透射峰对应缺陷模间的角频率间隔相等(如每一组透射峰从左向右数的第2条透射峰到下一组透射峰的第2条透射峰的角频率间隔相等，每一组透射峰从左向右数的第3条透射峰到下一组透射峰的第3条透射峰的角频率间隔相等)。从图4b～图4f也可以看出，相邻两组的对应缺陷模间的角频率间隔基本相等，但不是严格相等，这可能是因为，缺陷模不仅受到缺陷的影响，还受到整体结构的影响，要从解析公式表示该影响，还有待进一步深入研究。

正好说明了图2e和图3e中，每个禁带内都有一个透射峰，且都位于(ω/ω0)的奇数倍的位置。

4 结论

(1)在本文中所取参量下，每个禁带的归一化角频率宽度为2，每个禁带内都出现了与各参量相关的缺陷模，具有超窄带多通道滤波的特性。

(2)当k=1时，随着(ACB)n重复周期数n的增大，每个禁带都出现了n条超窄带缺陷模。

(3)当k≥2，n=1时，每个禁带内都出现了k条超窄带缺陷模。

(4)当 n≥2，nCdC=k×λ0/4时，每个禁带内有k组透射峰，每组透射峰都有n条缺陷模，每个禁带内总计有n×k条缺陷模，实现了多通道滤波的功能。与相同结构模型和相同结构参量下正折射率光子晶体的透射谱相比，一方面禁带宽度得到了展开，另一方面，其信道容纳能力得到了提高。

对于该光子晶体模型，禁带内窄带滤波器的通道数由(ACB)n重复周期数n(也就是缺陷的个数)和缺陷C的光学厚度nCdC共同决定。根据所需传输信息的信道数和信息所处的波段，可以调整缺陷的个数和厚度，以及其它介质的厚度，使光子晶体的结构满足信息传输的需求。这对基于1维光子晶体窄带多通道滤波器的设计和制备具有一定的参考价值。

［1］YABLONOVITCH E.Inhibited spontaneous emission in solid-state physics and electronics［J］.Physical Review Letters，1987，58(20):2059-2061.

［2］JOHN S.Strong localities of photons in certain disordered dielectric super lattices［J］.Physical Review Letters，1987，58(23):2486-2489.

［3］SU A.Defectmodes of one-dimensional photonic crystal for realizablemultiple channeled filter［J］.Laser ＆ Infrared，2010，40(5):532-536(in Chinese).

［4］SU A.Transmission spectrum of one-dimensional photonic crystal for realizing high-performance optical transmission function［J］.Infrared and Laser Engineering，2011，40(6):1101-1104(in Chinese).

［5］XIAO P，XIAO J.Tunable polarization filter based on one-dimensional photonic crystalwith liquid crystal defect［J］.Laser ＆ Optoelectronics Progress，2013(7):072301(in Chinese).

［6］DONG Q Y，MA S Y，WANG H，et al.Polarization band-pass filters based on one-dimensional dielectric and magnetic photonic crystals［J］.Acta Photonica Sinica，2011，40(7):1076-1081(in Chinese).

［7］DENG X H，LIU N H，AN L P.Tunablemultiple-channel filters based on photonic heterostructures using single-negative materials［J］.Chinese Science Bulletin，2009，54(10):1405-1409(in Chinese).

［8］DENG L E，WANG Y Sh，ZHOU X R.Multiple-channeled filters based on one-dimensional photonic crystal superlattice［J］.Journal of Beijing Jiaotong University，2008，32(3):53-55(in Chinese).

［9］CHEN Y H，MAO X H.Omnidirectional and a multiple-channeled filters of photonic quantum-well structures containing singlenegativematerials［J］.Acta Photonica Sinica，2009，38(3):576-580(in Chinese).

［10］SU A.Photonic crystal quantum wellwith function ofmulti-channel photonic filtering and amplifying［J］.Infrared and Laser Engineering，2013，42(3):727-732(in Chinese).

［11］LIU Q N.Analytical study on total reflection tunnel effect of1-D photonic crystal［J］.ActaOptica Sinica，2012，32(2):0219002(in Chinese).

［12］LIU Q N，HU Ch H.Polarization and total reflection tunnel effect of flat-panel photonic crystal［J］.Laser Technology，2012，36(1):114-117(in Chinese).

［13］ZHONG Y C，FANG Y T.Multi-channel frequency filter with high-Q value basing on ordinary one-dimensional photonic crystal［J］.Journal of Synthetic Crystals，2010，39(3):737-740(in Chinese).

［14］LIW S，ZHANGQ，HUANGH M，etal.Multi-channel frequency-multiplication filter based on photonic crystal［J］.Journal of Synthetic Crystals，2012，41(4):1125-1129(in Chinese).

［15］WANG X D，YAN K Zh，LIU F.Study of relations between band gap of photonic crystalsand the ratio of dielectric index［J］.Journal of Optoelectronics·Laser，2003，14(10):1063-1065(in Chinese).

［16］WANG TB，LIUNH.Band structuresand electric fieldsof onedimensional photonic crystals composed of alternate layers of lefthanded and right-handed materials［J］.Acta Physica Sinica，2007，56(10):5878-5882(in Chinese).

［17］BORN M，WOLF E.Principles of optics［M］.7th ed.Beijing:Publishing House of Electronics Industry，2009:59-61(in Chinese).

［18］LIU Q N.A new method of study the defectmode of one-dimensional photonic crystal［J］.Laser＆ Infrared，2008，38(8):799-801(in Chinese).

［19］LIU Q N.Resonace theory of the defectmode of1-D doping photonic crystal［J］.Acta Photonica Sinica，2012，41(4):446-450(in Chinese).

［20］ZHAO K H.New concept physics tutorial optics［M］.Beijing:Higher Education Press，2004:149(in Chinese).