基于多面循环Gerchberg-Saxton算法相位复原研究

彭金锰，李志鹏

(中国人民解放军69213部队21分队，喀什844900)

引 言

光在传输过程中，受传播介质、光学仪器误差、光学元件热或力影响下的变形等因素影响，光波会产生畸变，这些因素综合作用的结果就是成像模糊不清、分辨率降低［1］。高能激光系统中，受大气湍流带来的波前畸变影响，激光光束在远处无法有效聚焦，不能得到接近衍射极限的输出激光光束，激光在湍流大气中传输时，湍流将对它产生各种效应，如光强闪烁、相位畸变、光斑扩展和漂移等，这些效应均会导致激光光束质量的严重退化［2］，因此在实际的光学系统中，常需要测量畸变波前，为自适应校正等应用提供依据。

Gerchberg-Saxton(GS)算法在20世纪70年代由GERCHBERG和 SAXTON共同提出［3-4］，通过测量光瞳面和成像面的光强分布，利用迭代算法进行相位恢复。在实际应用中，GS算法可能会面临着光瞳面光强无法测量的情况，必须利用其它两个或多个位置处的光强信息，首先恢复这些位置的相位信息，然后利用光传输理论得到光瞳处的相位和振幅分布。在利用得到的相位信息计算光瞳的光场时，往往会增加误差，因此，必须提高焦面或离焦面的相位恢复精度。

作为一种局部搜索算法，GS算法极易陷入局部极值，而不能得到理想的精度［5-7］，尤其是在被恢复的相位比较复杂时。为了得到更精确的解，GU等人利用中间某两次的迭代得到的相位值进行加权作为下次迭代的初始条件，得到了更为准确的结果［8］。HUANG等人利用了3个面(1个输入面和2个输出面)的光强信息，采用与GS算法类似的迭代算法，并将当次的相位迭代值与上次的迭代值之差作为梯度方向，在下次循环中引入了该方向的一个附加值，大幅提升了收敛的速度［9］。本文中提供了一种扩展的循环GS算法，增加一个面的光强信息，使算法有机会跳出极值，达到比较高的精度。

1 光场传输理论

假定平面j的相位是 θj(j=1，2，…)，振幅分布为Fj且已知，则其光场为:

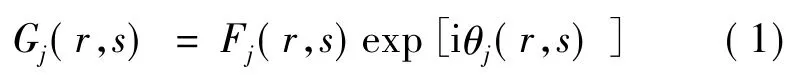
式中，r=1，2，3…，M;s=1，2，3…，N;M 和 N 分别为平面j两个方向的采样点数。使用角谱传输的方法，第 k个面的光场［10］为:

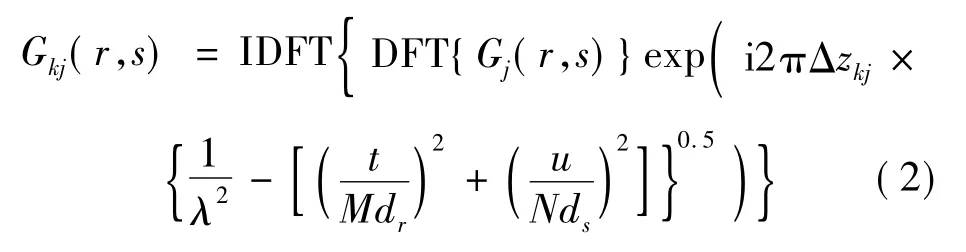
式中，DFT(discrete Fourier transform)和 IDFT(inverse discrete Fourier transform)分别表示正反离散傅里叶变换，λ为波长，t和u为傅里叶变换系数，dr和ds为第j个面的横向和纵向采样间距，与第k个面一致。Δzkj为第k个面到第j个面的传输距离。由第j个面计算第k个面光场，公式为:

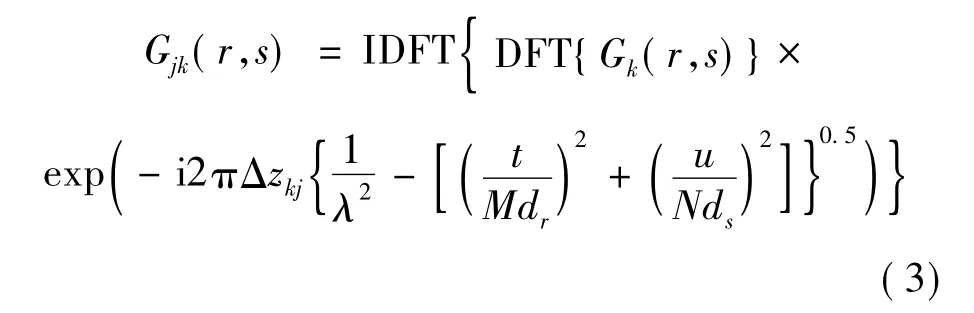
透镜后的光场可以由焦平面或离焦面光场通过(3)式计算，而通过透镜后，振幅可以认为不变，只是增加了一个相位因子θ:

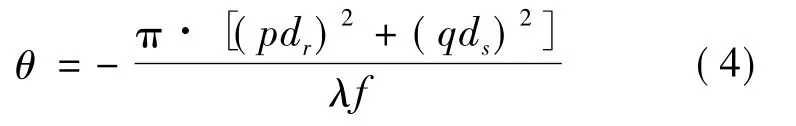
式中，f表示透镜焦距，p和q表示采样点坐标。

2 算法描述

光路中任意位置的两个或多个面光强分布已知的情况下，都可以利用GS算法得出这些面的相位分布，进而计算出其它位置的光场。本文中选择了焦平面和两个离焦面光强，如图1所示，对光瞳处的光场进行恢复。算法流程如下:(1)给定平面1的初始尝试相位φ0，与平面1的振幅结合;(2)利用(2)式计算平面2的光场，保留相位信息，与平面2的振幅结合;(3)利用(3)式，计算平面1的光场，保留相位信息，与平面1的振幅结合;(4)循环第2步至第3步至给定步数或评价函数达到给定值。

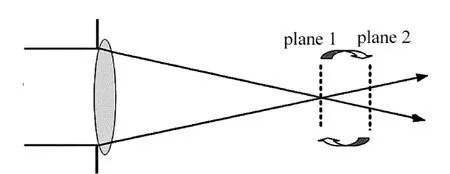
Fig.1 Schematic diagram of GS algorithm

只利用两个面的光强信息时，往往迭代几十次后收敛，得到的精度比较低，增加迭代次数并不能解决问题。为了能跳出局部极值，达到理想精度，这里提供了一种简单的循环方式，利用了3个面的光强信息进行迭代，如图2所示。首先利用平面1和平面2进行迭代，收敛后利用得到平面2的相位作为初始值，与平面2的振幅结合，进入平面2与平面3之间的迭代，得到新的平面2的相位信息。循环上述过程几次。最后以计算得到的平面2的光场，利用(3)式和(4)式逆向计算光瞳处的光场。

Fig.2 Schematic diagram of circulatory GS algorithm

3 改进算法仿真结果与分析

3.1 高斯光束恢复

透镜前的光场振幅为高斯分布，波前由4阶至10阶ZERNIKE多项式［11］生成，系数分别为 2.9，0.72，-1.2，0.72，-0.96，-0.72，0.72 和 -0.24，光瞳区域内波长畸变约为0.3λ，以后的例子中，光瞳处波前分布一致。波长为1.064μm，透镜焦距500mm，光瞳直径6mm，采样点数为512×512。定义振幅误差R为:

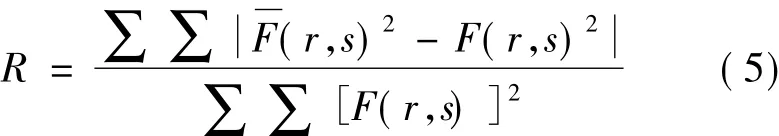
焦平面和距离焦平面150mm和300mm处得到的振幅分布，如图4所示。

Fig.3 Amplitude and phase of round pupil plane a—amplitude b—phase

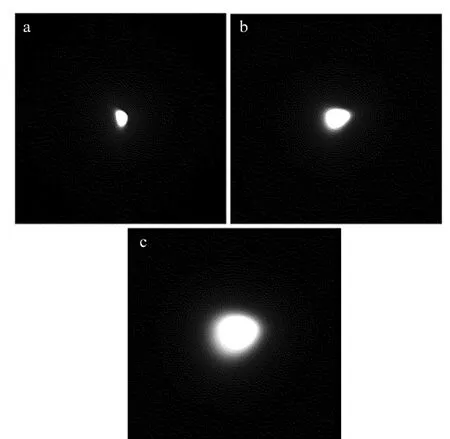
Fig.4 Amplitude of focal plane and two defocused planes a—focal plane b—150mm c—300mm

以零相位面作为算法的初始值，采用改进GS算法，最终恢复出来的透镜前的振幅和分布(见图5)，图5c表示复原出的波前残差，单位为λ，后文中同此表示。

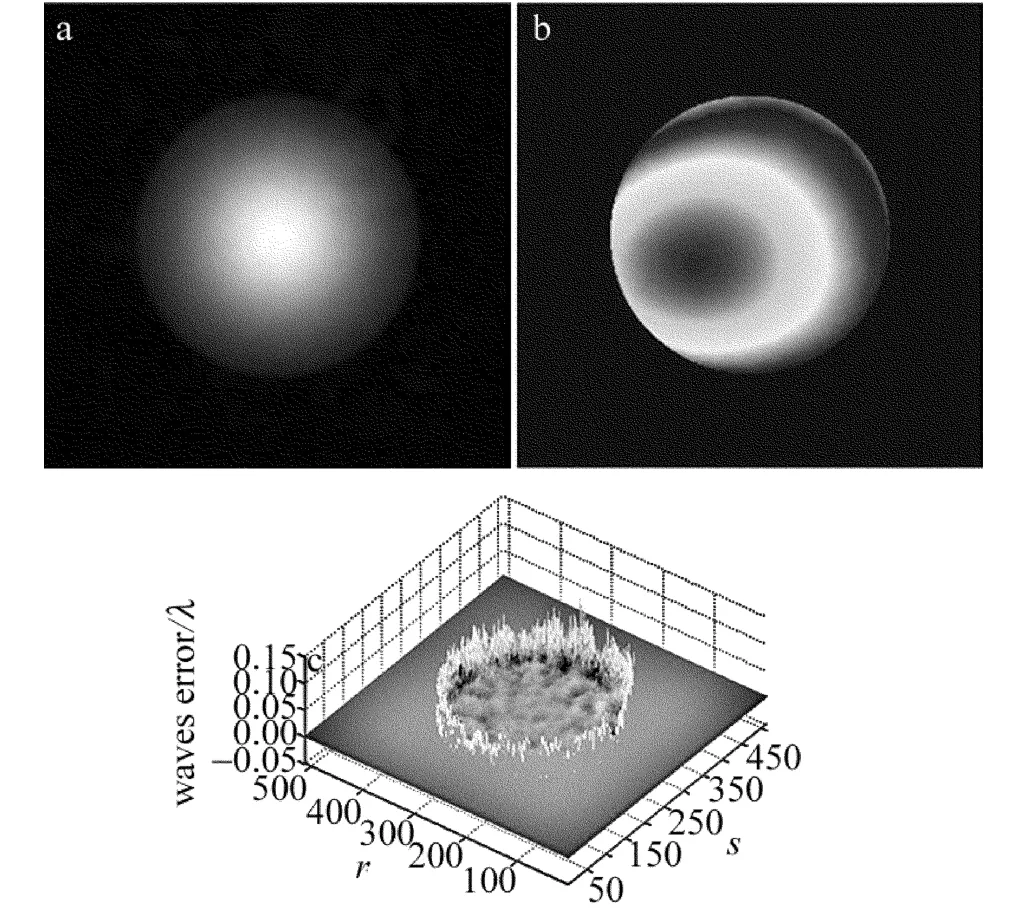
Fig.5 Retrieved amplitude，phase and residual phase error of round pupil planea—amplitude b—phase c—phase error

恢复出的波前误差为 0.007λ，如果不考虑0.4mm的边缘区域，光强在峰值的0.035以内区域精度达到了0.002λ。

尽管透镜前的光场未知，但在仿真中仍然可以监视光瞳平面的恢复出的振幅与实际振幅分布的误差，如图6所示。

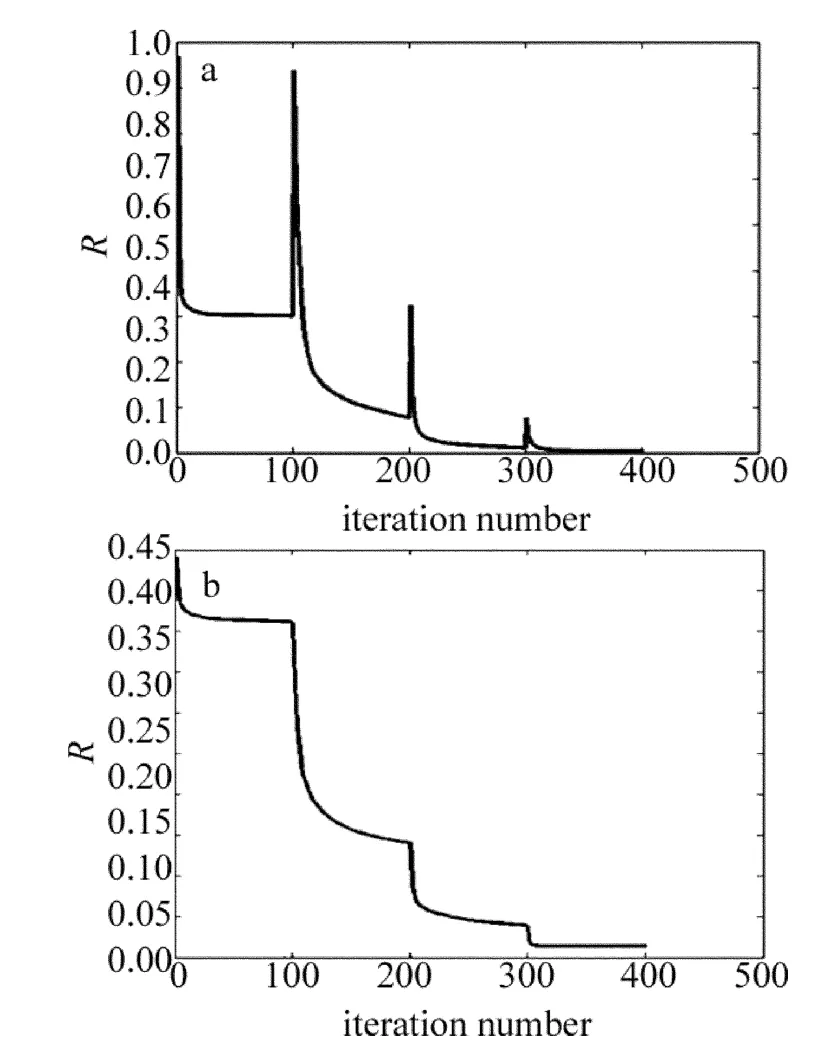
Fig.6 Amplitude error of plane 2 and round pupil plane vs.iteration numbera—plane2 b—pupil plane

前100次迭代即为GS算法，由图6a可以看出，GS算法迭代几十次后左右陷入极值，复原出的振幅误差较大，复原出的波前分布几乎无参考价值。这种情况在进行迭代的光场波前相对复杂时更容易发生。改进后，进入下次循环，算法跳出了局部极值，最初平面2振幅误差大幅增加，随后迅速下降，收敛到更小的值。而透镜前的振幅误差一直下降，表明复原出的光场更接近实际分布。

3.2 圆形平顶光束恢复

对圆形平顶光束进行相位恢复时，GS算法更容易陷入局部极值，在经过10次循环后，最终波前误差为0.0049λ。恢复结果如图7所示。

与高斯光束波前恢复相比，需要更多循环次数，而且振幅和相位恢复结果弱于高斯光束恢复效果。

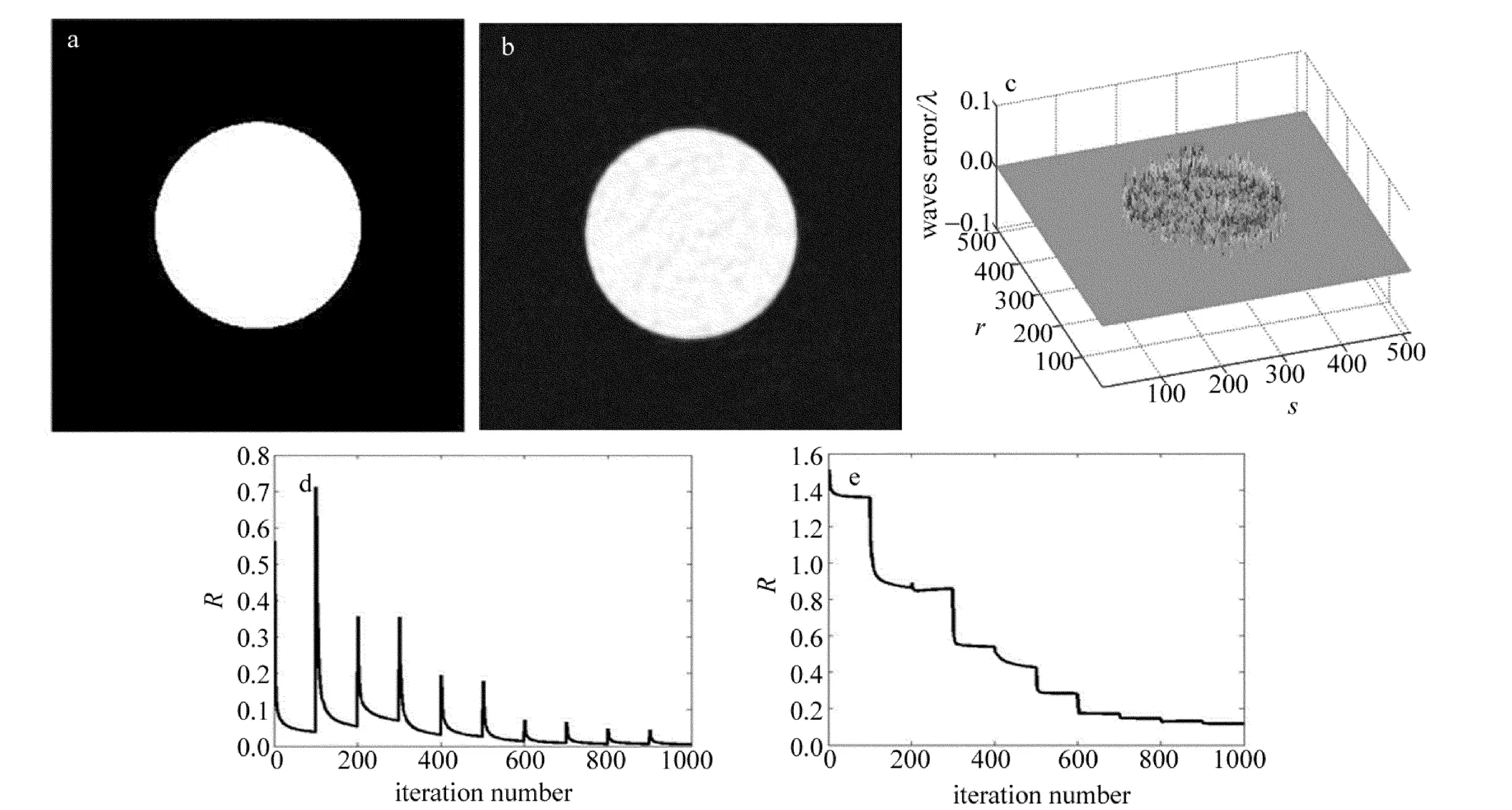
Fig.7 a—real amplitude of pupil plane b—retrieved amplitude of pupil plane c—phase error of pupil plane d—amplitude error of plane2 vs.iteration number e—amplitude error of pupil plane vs.iteration number

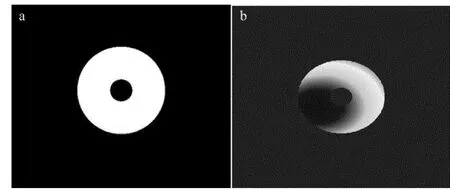
Fig.8 Amplitude and phase of annulus pupil plane a—amplitude b—phase

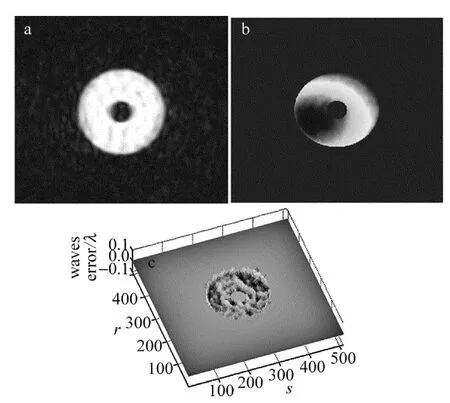
Fig.9 Retrieved amplitude，phase and phase error of annulus pupil plane a—amplitude b—phase c—phase error

3.3 圆环光束恢复

光瞳处的圆环内径1mm，外径4mm。光束如图8所示。恢复出的振幅和波前残差如图9所示，最终波前误差为0.0064λ。

在对内径为2mm、外径4mm的圆环光束进行恢复时，算法经过多次循环后精度未有提升，算法在多循环中，只在两个局部极值间变动，不能进一步提高精度，这与首次循环迭代得到的结果精度不高有关。

4 结论

在光瞳处振幅未知的情况下，采用用GS算法，利用焦平面和附近一个平面上的光强信息对光瞳平面上的光场进行复原，误差较大，以至于无参考价值。增加一个平面后，可以比较准确地重建光瞳光场，事实上，每一处的光场都可以得到准确复原，优于只利用两个面光强信息的迭代得到的结果。信息量的增加，使得算法能够有效地跳出局部极值，达到更准确的结果。

［1］WANG X，ZHAO D Z，MAO H，et al.The developmentof phase diversity［J］.Optical Technique，2009，35(3):454-460(in Chinese).

［2］GE X L，FENG X X，FAN Ch Y.Progress of the study of phase discontinuity of laser propagation through atmosphere［J］.Laser Technology，2012，36(4):485-489(in Chinese).

［3］GERCHBERG RW，SAXTON W O.Phase determination from image and diffraction plane pictures in electron microscope［J］.Optik，1971，34(3):237-246.

［4］GERCHBERG RW，SAXTONW O.A practical algorithm for determination of phase from image and diffraction plane pictures［J］.Optik，1972，35(2):275-284.

［5］FIENUP JR.Phase retrieval algorithms:a comparison［J］.Applied Optics，1982，21(15):2758-2769.

［6］FIENUP JR.Phase-retrieval algorithms for a complicated Optical system［J］.Applied Optics，1993，32(10):1737-1746.

［7］RODDIER C，RODDIER F.Combined approach to the hubble space telescopewave-front distortion analysis［J］.Applied Optics，1993，32(15):2992-3008.

［8］GU X，XU K Sh.Some improvements on the GS algorithm in phase retrieval problem［J］.Journal of Fudan University，2000，33(2):205-211(in Chinese).

［9］HUANG L X，YAO X，CAID M，et al.A high accuracy and fast iterative algorithm for phase retrieval［J］.Chinese Journal of Lasers，2010，37(5):1218-1221(in Chinese).

［10］BRADY G R，FIENUP JR.Nonlinear optimization algorithm for retrieving the full complex pupil function［J］.Optics Express，2006，14(2):474-486.

［11］NOLL R J.Zernike polynomial and atmospheric turbulence［J］.Journal of the Optical Society of America，1976，A66(3):207-211.