非对称光学图像加密系统的已知公钥攻击

丁湘陵，袁 倩，张乐冰

(怀化学院物理与信息工程系，怀化418008)

引 言

伴随着计算机软硬件技术的快速发展和网络的广泛使用，信息安全问题变得越来越严峻。近年来，由于光学加密技术具有并行的内在特性和光学信号处理的多维特性，在某种意义上比数字方法更具有优越性，因而探索和开发光学加密技术具有更高的学术和应用价值。当前讨论最多的都是基于1995年REFREGIER和JAVIDI提出的双随机相位编码加密技术［1］(double random phase encoding technique，DRPE)，例如分数傅里叶变换系统、扩展分数傅里叶变换系统和菲涅耳衍射系统等［2-7］。然而，这些基于DRPE的加密技术都是通过在加密过程中增加一系列额外的密钥来提供更多的信息安全。但是，它们依然基于DRPE加密技术，因此它们特有的线性特性导致其不能抵抗某种特定的攻击、例如已知明文攻击，选择明文攻击或唯密文攻击等［8-11］。从加密学观点看，基于DRPE技术提出的加密方法［2-7］都是加密密钥和解密密钥相同的对称加密系统，在网络环境下对称加密系统容易遭受一些安全问题，例如密钥的安全分发和管理。为了克服这种情况，2010年WANG和PENG等人利用相位截断的非线性操作改变DRPE的线性特性，并提出基于相位截断傅里叶变换(phase-truncated Fourier transform，PTFT)的非对称光学图像加密系统［12］。在该系统的加密过程中，通过使用相位截断处理和两个公开的随机相位掩膜产生具有实值和白噪声特性的密文;在解密过程中，使用两个加密过程中利用振幅截断处理非线性产生的与加密密钥完全不同的解密密钥来恢复原文［12-13］。尽管相位截断的非线性操作使得基于PTFT的非对称光学图像加密系统具有很强的健壮性，可是WANG和ZHAO等人通过“特殊攻击”的办法可以分析得到非对称光学图像加密系统的明文和解密密钥［14］。“特殊攻击”需要攻击者首先截获密文，再在攻击实施过程中使用傅里叶迭代算法恢复明文和解密密钥，难度较大且复杂。

本文中通过分析非对称光学图像加密系统的安全性提出一种已知公钥的攻击方法。相对于WANG和ZHAO等人提出的基于傅里叶迭代算法的“特殊攻击”［14］，本文中所提出的攻击方法仅仅只需要公开的加密密钥，从而获得非对称光学图像加密系统的通用解密密钥，再利用该通用解密密钥破解非对称光学图像加密系统，恢复明文。整个攻击过程实施的难度大大降低，除了公开的加密密钥，无需额外的资源。

1 非对称光学图像加密系统的已知公钥攻击

1.1 非对称光学图像加密系统

基于相位截断傅里叶变换的非对称光学图像加密系统也同样利用4f系统来实现。在加密过程中，输入图像f(x，y)首先在空间域受到随机相位掩膜R1(x，y)(输入平面密钥)的调制;调制后的图像经过傅里叶变换和非线性的相位截断操作后，在频率域被随机相位掩膜R2(u，v)(频谱面密钥)滤波;滤波后的图像经过傅里叶逆变换和非线性的相位截断操作后，在输出平面上得到密文。整个加密过程表示为:

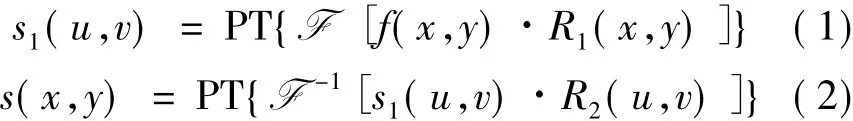
式中，f(x，y)，s1(u，v)和 s(x，y)分别表示输入图像、傅里叶平面的光强分布和密文，R1(x，y)和R2(u，v)分别定义为 exp［i2πb(x，y)］和 exp［i2πn(u，v)］，b(x，y)和 n(u，v)是均匀分布在［0，1］上的两个独立噪声序列，PT{}，{}和{}分别表示相位截断操作，傅里叶变换和傅里叶逆变换。

在加密过程中同时也会产生两个解密密钥W1(x，y)和 W2(u，v)，产生过程如下:

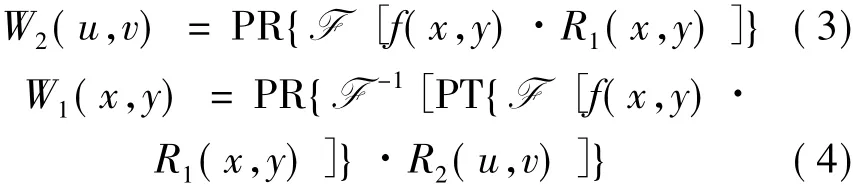
式中，PR{}表示振幅截断操作。

解密过程中，首先将密文s(x，y)置于非对称光学图像加密系统的输入平面，在空间域受到解密密钥W1(x，y)的调制;调制后的密文经过傅里叶变换和相位截断操作后，在频率域用解密密钥W2(u，v)滤波;滤波后的结果再经傅里叶逆变换和相位截断操作，就能恢复出明文f(x，y)。整个解密过程产生如下:

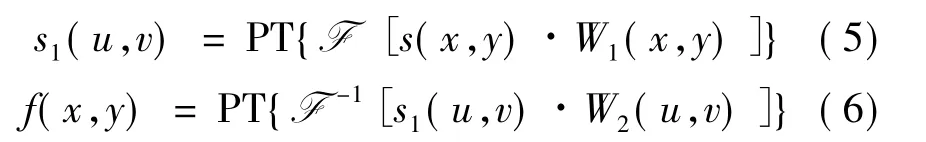
1.2 非对称光学图像加密系统的已知公钥攻击

在对密码系统进行安全性分析时，通常认为攻击者已经截获所需的密文，同时知晓密码系统加密、解密算法的整个工作原理［15］。下面利用本文中提出的已知公钥攻击方法来分析基于相位截断傅里叶变换的非对称光学图像加密系统的安全性。假定攻击者已经获取公钥 R1(x，y)和 R2(u，v)，并且选择一幅幅值全为1的实值图像，攻击过程由如下两个步骤组成。

1.2.1 利用已知公钥获得通用解密密钥 在已知公钥(R1(x，y)和 R2(u，v))的条件下，攻击者利用一幅幅值全为1的原始实值图像c(x，y)，对c(x，y)使用已知公钥(R1(x，y)和R2(u，v))在空间域调制和频率域滤波，利用振幅截断操作获取通用解密密钥，步骤如下:

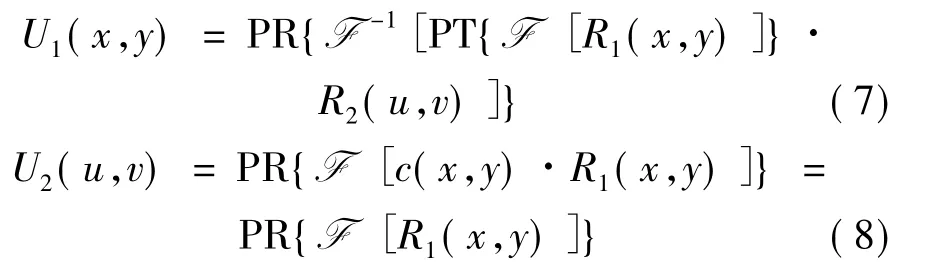
式中，R1(x，y)定义为 exp［i2πb(x，y)］，R2(u，v)定义为 exp［i2πn(u，v)］，b(x，y)和 n(u，v)是均匀分布在［0，1］上的两个独立噪声序列。

1.2.2 利用通用解密密钥获得明文 由第1.2.1节中得到，通过利用(7)式和(8)式能获取进行解密所需的通用解密密钥U1(x，y)和U2(u，v)。而本文中所提出的攻击方法就是在解密过程中将通用解密密钥 U1(x，y)和 U2(u，v)分别替换(5)式和(6)式中的解密密钥W1(x，y)和W2(u，v)，而解密过程不作任何改变。破解过程如下:

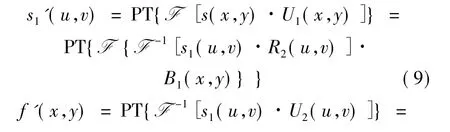
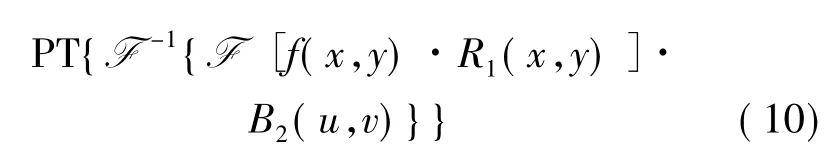
式中，B1(x，y)和 B2(u，v)为模糊因子，表示如下:

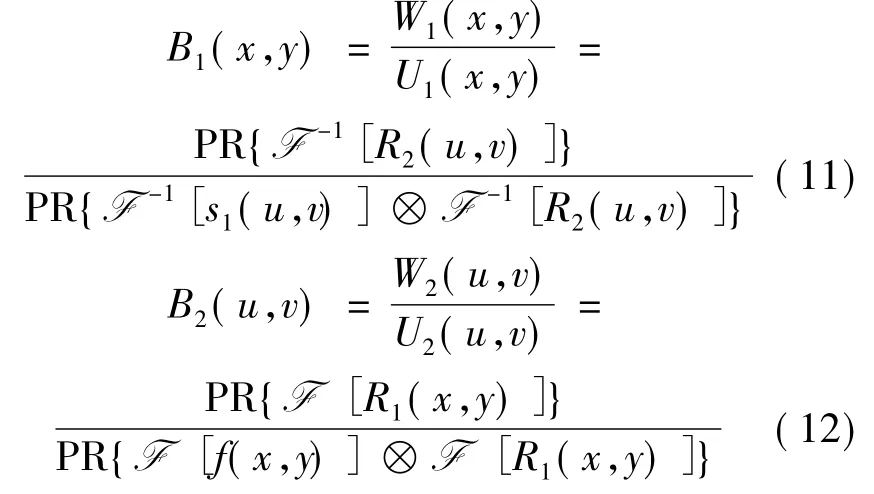
2 实验仿真

为验证本文中提出的已知公钥攻击方法的有效性，在MATLAB 7.0环境下进行仿真。首先利用已经公开的用于加密的两块随机相位掩膜R1(x，y)和R2(u，v)(如图1a和图1b所示)，应用相位截断操作获得通用解密密钥;然后利用通用解密密钥和非对称光学图像加密系统的解密过程解密截获的密文，从而得到明文。图2a是灰度实值明文图像，图2b是图2a加密后的密文，图2c是使用本文中所提方法破解后的结果。图3a是二值明文图像，图3b是图3a加密后的密文，图3c是使用本文中所提方法破解后的结果。图4a是通过低频滤波处理的具有大量低频分量的灰度实值明文图像，图4b是图4a加密后的密文，图4c是使用本文中所提方法破解后的结果。由图2～图4可知，无论明文图像是否具有大量低频分量，本文中提出的已知公钥攻击方法都能获得较好的破解效果。

Fig.1 Two public random phasemasks of asymmetric optical cryptosystema—R1(x，y) b—R2(u，v)

Fig.2 The simulation results of gray-plaintext imagea—original cameraman image b—encrypted cameraman image c—the result of the known-public key attack

Fig.3 The simulation results of binary-plaintext imagea—original circle image b—encrypted circle image c—the result of the known-public key attack

Fig.4 The simulation results of filtered-plaintext imagea—filtered-plaintext image b—encrypted image c—the result of the known-public key attack

为进一步说明本文中所提攻击方法的破解效果，引入归一化均方误差(normalizedmean square error，NMSE)N 和图像逼真度(image fidelity，IF)I来评价破解结果的质量。分别定义如下:

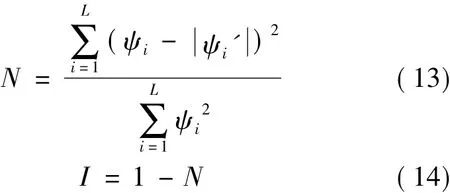
式中，ψi和ψi'分别表示图像中的某个像素点灰度值和对应的破解结果值，L表示图像中具有的像素总数。由(13)式和(14)式可知，归一化均方误差值越小，破解图像与原始图像的差异就越小，图像逼真度值就越高。根据(13)式和(14)式对灰度图像、二值图像和通过低频滤波处理的具有大量低频分量的灰度实值明文图像进行NMSE和IF值计算，计算结果见表1。

从表1可以看出，使用已知公钥攻击方法得到的解密结果，灰度图像的解密效果比二值图像解密效果更好。主要的原因在于灰度图像的模糊因子B1(x，y)和 B2(u，v)的平均结果分别为 2.9172 和2.6137;二值图像的模糊因子 B1(x，y)和 B2(u，v)的平均结果分别为6.4703和8.5429;而通过低频滤波处理的具有大量低频分量的灰度实值明文图像的模糊因子B1(x，y)和B2(u，v)的平均结果分别为0.9804和0.9171。由此可得，模糊因子值越逼近1，破解效果越好，仿真结果与理论推导一致。

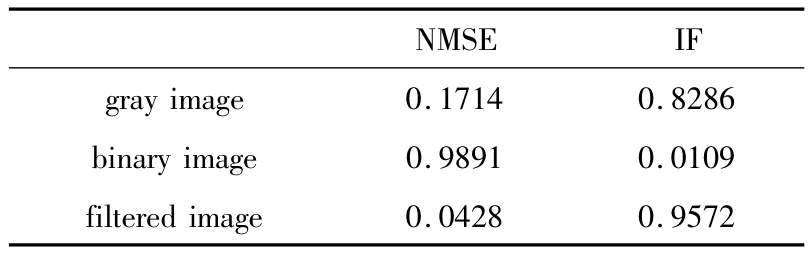
Table 1 Calculation results

3 结论

阐述了基于相位截断傅里叶变换的非对称光学图像加密系统的已知密钥攻击方法的理论推导过程，虽然推导出的通用解密密钥与真实密钥相差一个模糊因子，但如果输入图像是实值图像且具有大量低频分量，其模糊因子基本上逼近1，从而可以达到较好的破解效果。通过模拟实验证明，虽然相位截断的非线性操作使得基于PTFT的非对称光学图像加密系统具有很强的健壮性，但是，一旦将加密密钥公布出来，通过使用已知公钥攻击方法依然能恢复原图像，所以其安全性并没有提高。同时，与特殊攻击方法相比，本文中提出的已知密钥攻击方法只需要公开的加密密钥，无需额外的资源，因此更具实际意义。

［1］REFREGIER P，JAVIDIB.Optical image encryption based on input plane and Fourier plane random encoding［J］.Optics Letters，1995，20(7):767-769.

［2］SITU G H ，ZHANG J J.Double random phase encoding in the Fresnel domain ［J］.Optics Letters，2004，29(14):1584-1586.

［3］LIN R，LIU Q N，ZHANG C L.A new fast algorithm for gyrator transform［J］.Laser Technology，2012，36(1):50-53(in Chinese).

［4］WANG X G，ZHAODM，CHEN L F.Image encryption based on extended fractional Fourier transform and digital holography technique［J］.Optics Communications，2006，260(2):449-453.

［5］HWANG H E，CHANG H T，LIE W N.Fast double-phase retrieval in Fresnel domain using modified Gerchberg-Saxton algorithm for lensless optical security systems［J］.Optics Express，2009，17(16):13700-13710.

［6］DENG X P，ZHAO D M.Multiple-image encryption using phase retrieve algorithm and inter-modulation in Fourier domain［J］.Optics and Laser Technology，2012，44(2):374-377.

［7］HENNELLY B，SHERIDANJT.Optical image encryption by random shifting in fractional Fourier domains ［J］.Optics Letters，2003，28(4):269-271.

［8］PENG X，WEI H Zh，ZHANG P.Chosen plaintext attack on double random-phase encoding in the Fresnel domain［J］.Acta Physica Sinica，2007，56(7):3924-3930(in Chinese).

［9］PENG X，ZHANG P，WEIH Zh，et al.Known-plaintext attack on double phase encoding encryption technique［J］.Acta Physica Sinica，2006，55(3):1130-1136(in Chinese).

［10］WEIH Zh，PENG X，ZHANG P，etal.Chosen-Plaintext attack on double phase encoding encryption technique［J］.Acta Optica Sinica，2007，27(5):824-829(in Chinese).

［11］PENG X，TANG H Q，TIAN J D.Ciphertext-only attack on double random phase encoding optical encryption system ［J］.Acta Physica Sinica，2007，56(5):2629-2636(in Chinese).

［12］WANG Q，PENG X.Asymmetric cryptosystem based on phasetruncated Fourier transforms［J］.Optics Letters，2010，35(2):118-120.

［13］DING X L.Asymmetric optifcal image cryptosystem based on sphericalwave illumination［J］.Laser Technology，2013，37(5):577-581(in Chinese).

［14］WANG X G，ZHAO D M.A specific attack on the asymmetric cryptosystem based on the phase-truncated Fourier trans-forms［J］.Optics Communications，2012，285(6):1078-1081.

［15］STALLINGSW.Cryptography and network security:principles and practice［M］.2nd ed.Upper Saddle River，New Jersey，USA:Prentice Hall，1999:24-26.