基于极坐标变换的相位扫描定中方法

马国鹭， 赵 斌

(华中科技大学 机械科学与工程学院， 武汉 430074 )

基于极坐标变换的相位扫描定中方法

马国鹭， 赵 斌*

(华中科技大学 机械科学与工程学院， 武汉 430074 )

为了实现无衍射光斑作为直线基准在复杂噪声背景下仍能快速精确定中的目的，采用相位扫描的方法来获得极坐标系下的无衍射光斑相位角随极角的振荡起伏，对无衍射光斑在环向上的相位与标准正弦条纹的相位对比获得其偏离量，通过多次迭代便实现了无衍射光斑的定中，并进行了理论分析与测试实验。结果表明，该算法具有良好的抗噪能力、较低的计算时耗和亚像素级的定中精度。

图像处理；信号处理；衍射；相位扫描；无衍射光斑

引 言

光束在工程中常被作为直线的基准(譬如高斯光束)，但是传统的方式在工程应用中受到多种局限[1-3]。DURNIN将麦克斯韦波动方程下一簇沿传播方向的截面上光强分布不变的特解定义为无衍射光，由于其在无源的自由空间中可保持恒定不变的空间传输特性(无离焦、无畸变、抗背景干扰和高定心精度等特性)，因此，无衍射光斑中心传播轨迹可作为理想的直线基准，尤其是在精密工程中，譬如姿态角测量[4]与大尺度空间中的直线度测量[5]。而在基于无衍射光束作为基准的应用中,关键就是对无衍射光斑中心的定中处理。

目前，适用于无衍射光斑定中算法有如下几种：(1)图像灰度重心法[6]，这种方法计算简单，符合理论上的无衍射中心位置处光斑最强的分布特性，但在波阵面存在误差时，衍射的光斑光强分布难以预计，因此实际上图像的灰度重心有相当大的不确定范围；另一方面直接根据灰度值来确定中心，其位置极限精度最高为一个探测单元的尺度(对现有图像探测器，探测单元尺寸约为5μm)，这往往达不到某些精密测量的要求;(2)基于图像边缘提取的Hough变换的圆检测法[7]与圆拟合法[8],Hough圆检测法是将图像空间中的边缘点映射到参量空间中，然后将在参量空间中得到的所有坐标点元素对应的累加值进行累加统计，根据累加值判断圆的大小和圆心所在位置，该方法具备良好的鲁棒性和圆识别能力；而圆拟合法则是根据最小二乘原理拟合逼近圆，计算速度快；然而这两种圆检测方式都是依赖于边缘提取的质量，并且传统Hough圆检测法存在计算量大、耗费内存空间、参量空间峰值点被次峰值点包围、易造成漏检或误检等缺陷，而圆拟合法不具备圆的识别能力，在对背景噪声点多的情况下拟合偏差较大;(3)直接对灰度图进行处理的数字莫尔条纹扫描定中算法[9]与基于圆环滤波的匹配定中算法[10]。该方法类比计量光学中的莫尔条纹技术，采用环形数字光栅与无衍射光图像重叠，合成莫尔条纹效应，通过相位扫描获得图像各点对应的相位锥，根据相位锥与中心点的映射关系实现对无衍射光斑的定中。这种方法具有良好的鲁棒性和亚像素的定心精度，但相位锥的计算耗费巨大，全部图像数据都参与每步迭代计算导致计算收敛缓慢。并且上述的所有算法都无法自动判断与剥离在无衍射光斑中心区域受破坏的环形纹理区域。

作者针对无衍射光斑同心圆环的纹理特征，结合工程实际中其中心区域更易受噪声影响，提出一种基于极坐标变换的相位扫描定中算法。该方法通过分区相位对比可自动识别并剥离受噪声影响的无衍射光斑中心环区，由外圆环向内的搜索机制，降低了计算时耗的同时，还保证了定中精度，且其收敛性不依赖于初始坐标。该方法更能适应于实际工程需要。

1 定中原理

理论上无衍射光束的光强分布在径向上呈第一类零阶贝塞尔函数分布，其理论中心就出现在光强最大处，也即贝塞尔函数的极大值点位置，如图1a所示。然而实际中合成的近似无衍射光斑常因光束照射强度、图像传感器的采样位数及其曝光时间、增益等参量的设置等因素，导致图像中心区域性饱和；因光束的倾斜照射，导致无衍射光斑中心分裂[11]；因axicon锥面形貌的加工误差，引起同心环形条纹波动起伏或断裂[12-13]。图1b中展示了受影响的无衍射光斑图像。

Fig.1 Image of non-diffraction beam

a—ideal non-diffracting was generated by using numerical simulation b—non-diffracting spot was affected by noise

尽管实际无衍射光斑在径向上的光强服从贝塞尔函数分布受到了破坏，但是合成的近似无衍射光斑在轴向上的传播恒定不变、圆环的同心以及径向上的整体起伏趋势特性依然完好，则沿无衍射光斑理论中心点[xc,yc]将图像展开成极坐标形式：

(1)

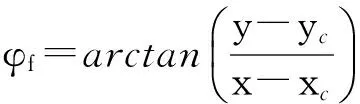
使用计算机合成角频率为 ωf的一个正弦gs=sin(ωfρ+φg)和余弦gc=cos(ωfρ+φg)数字条纹，其中φg为初始相位信息,是一个常量。将极坐标转换后的图像f(ρ,φf)逐点乘以正弦数字条纹gs可得如下：

(2)

对(2)式沿极径ρ进行整倍数周期n定积分可得：

(3)

类似地将gc乘上无衍射光束图像，并对其极径ρ的整倍数n周期定积分：

(4)

联立(3)式与(4)式便求解得出在极角φf处的初始相位角为：

(5)

故此在理论中心坐标位置(xc,yc)处时，各极角向上的相位为合成的数字条纹为初始相位φg与无衍射光斑初始相位φf之和，是一个常量，也即：∂η(ωf)/∂ωf=0。

如图2a所示，当图像极坐标变换原点从(xc,yc)偏移至(xc′,yc′)后，图像灰度映射关系如图2b所示，描述如下：

(6)

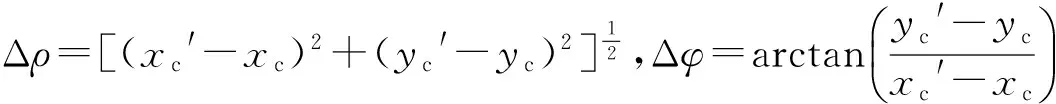
(7)

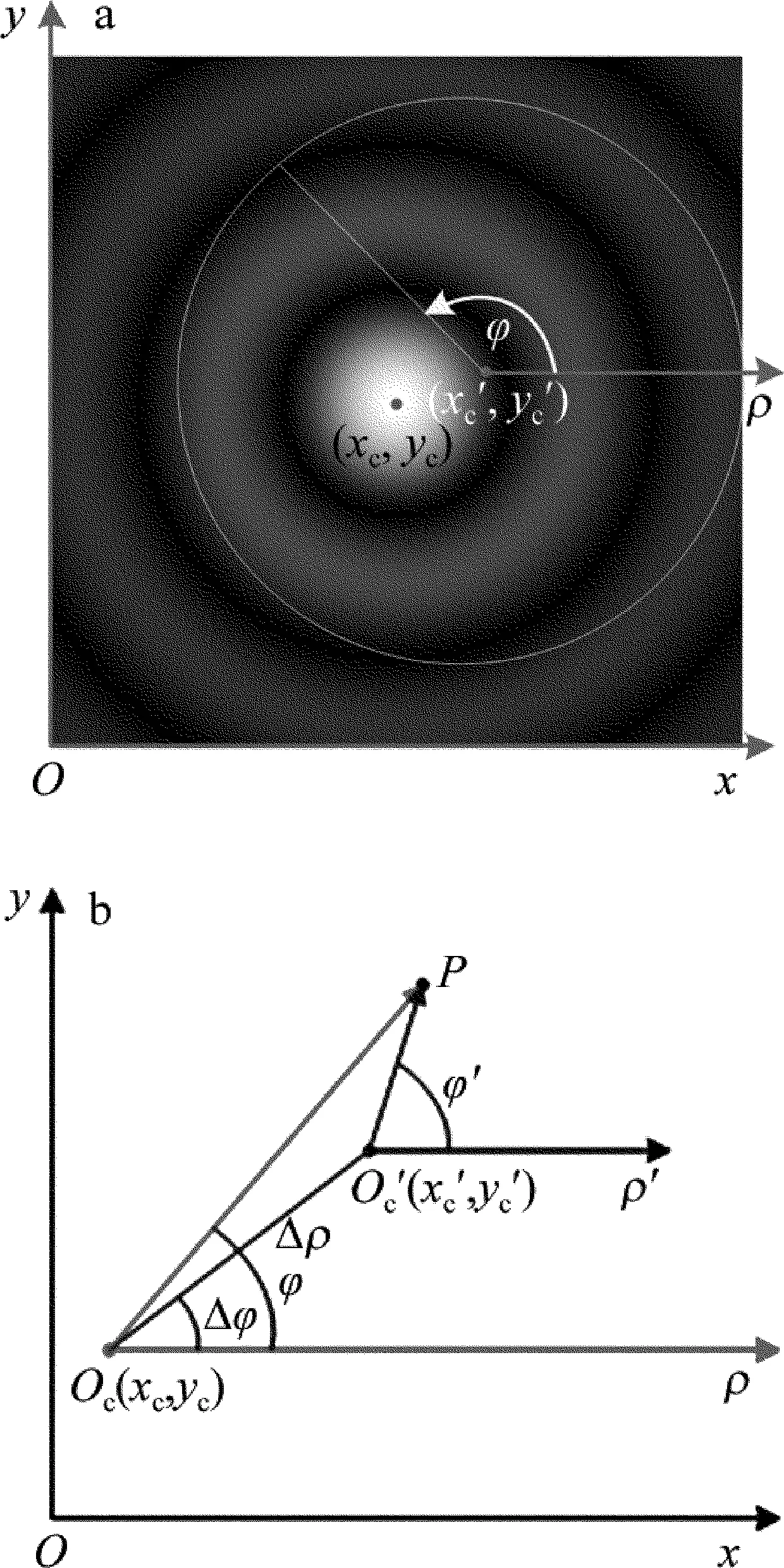
Fig.2 Polar coordinate transformation

a—theimageofthenon-diffractingbeamwasexpandedinthepositionofidealcentreandoutoffb—therelationshipofpolarcoordinateinpositioncommoncentreandoutoff

(8)

类似(1)式,对(8)式按(2)式～(4)式的步骤进行处理，可得以点(xc′,yc′)进行极坐标变换后各径向上相位角分布与偏移量Δρ的关系：

(9)

(9)式表明,当圆周内的各径向上的相位是一个带有恒定偏置量(初始相位之和φg+φf)呈余弦起伏变化的曲线，而其振幅大小正比于距理想中心的偏离量值Δρ，也即▽η′(φf′)∝Δρ；故此当Δρ=0，也即在理论中心展开后的无衍射光斑图像的相位分布为直线，如图3a所示。采用方差来衡量在坐标(xc′,yc′)点处对无衍射光斑进行极坐标后相位函数的起伏量，如下：

(10)

式中，E(η′)，D(η′)分别表示的是变量η′的数学期望与方差。

(10)式表明,评价相位起伏量ν(xc′,yc′)与周向角φf′和偏离角Δφ不相关，仅与偏离理论中心的平方成正比，在理论中心时最小且为0，如图3b所示。

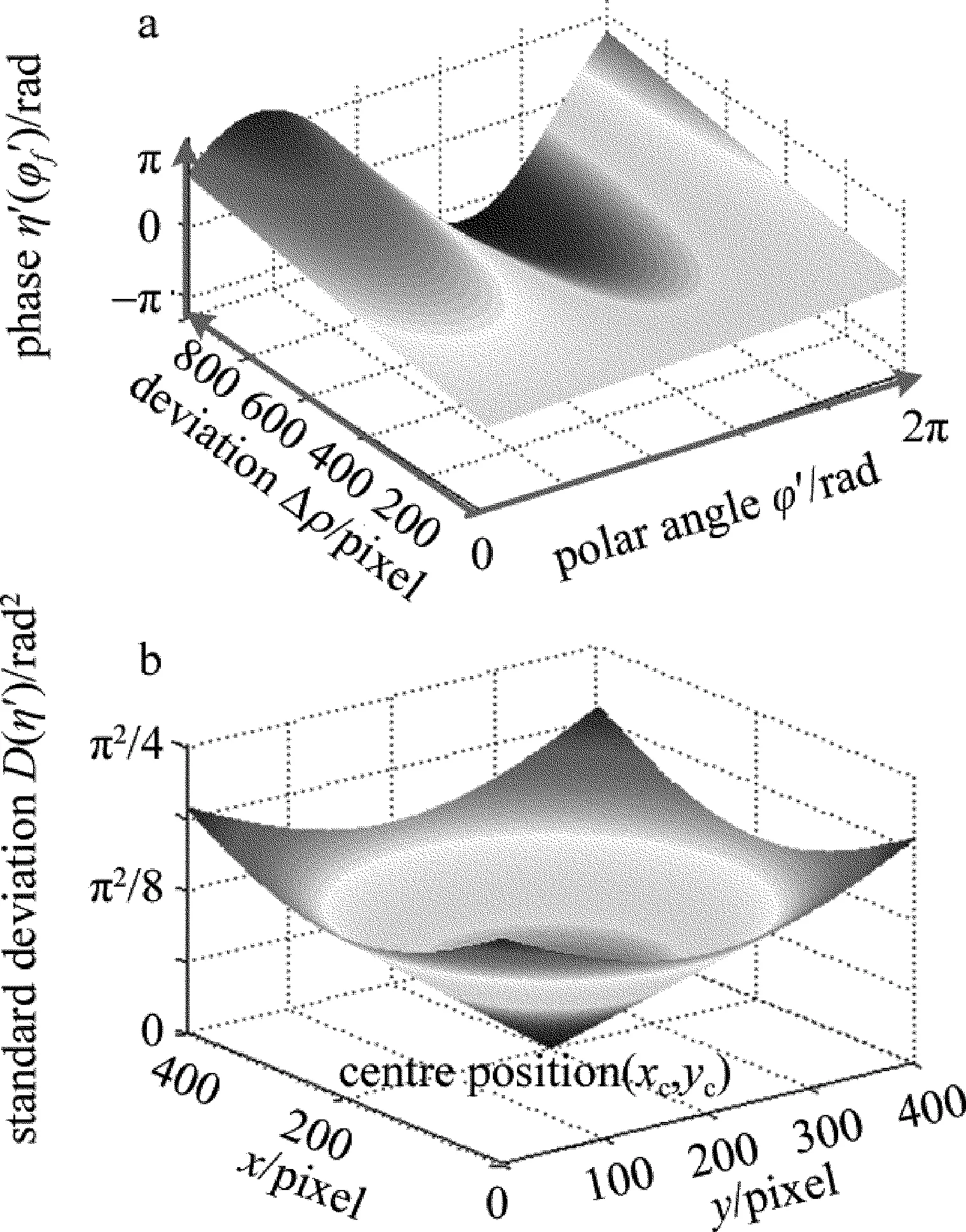
Fig.3 Distribution of phase along with deviation

a—the phase along deviation and polar angle b—the standard deviation of phase along deviation in the plane of non-diffracting image

假设当图像中存在光强分布为N(ρ,φf)的背景噪声时，由其导致的各径向上的相位误差为φN(φf′)，则各径向上相位角分布为：

(11)

结合(10)式则得整理η′(φf′)方差如下：

(12)

由(12)式表明,在背景噪声时，相位评价函数仅添加了一项常数项，而依然正比于距离理想中心的偏离量Δρ，并且在理论中心处最小但不为0。

2 算法实现

根据上述理论，具体算法实现步骤见下。

(1)采用重心法计算出无衍射光斑图像光斑的大致初始位置中心坐标(xc″,yc″) ，对尺寸为m×n大小的无衍射光斑图像Mf，初始中心计算如下：

(13)

(2)将图像Mf以(xc″,yc″)为初始中心，转换为极坐标系下的灰度图Mρ(ρi,φj)。其中呈清晰波浪纹理是由于初始中心的偏离理论中心所致，而在图中靠近极径区域且呈椭圆形亮斑，是由于初始中心偏离理论中心的距离远大于零级衍射环半径，椭球形光斑愈大表明偏离的环极就愈多。

(14)

(3)沿极径将图像Mρ(ρi,φj)等分成两部分，即Mρ,up(ρi,φj)与Mρ,down(ρi,φj)，将生成的正弦与余弦矩阵信号Ms与Mc也分别分成对应的上下两部分Ms,up(ρi),Ms,dowm(ρi)与Mc,up(ρi),Mc,down(ρi)信号，并分别与变换后的极坐标系下的灰度图进行如(5)式～(7)式的求解上下两部分图像的相位角η0，up′(φj′),η0，down′(φj′)，离散计算式如下：

(15)

(4)按如下计算式对η0,up′(φj′)和η0,down′(φj′)进行解包络计算,得到上下两幅图像的解包络相位角ηup′(φj′),ηdown′(φj′)：

(16)

(5)对解包络后的相位ηup′(φj′),ηdown′(φj′)进行方差计算:

(17)

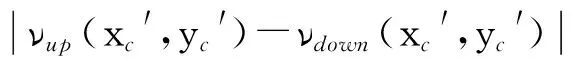
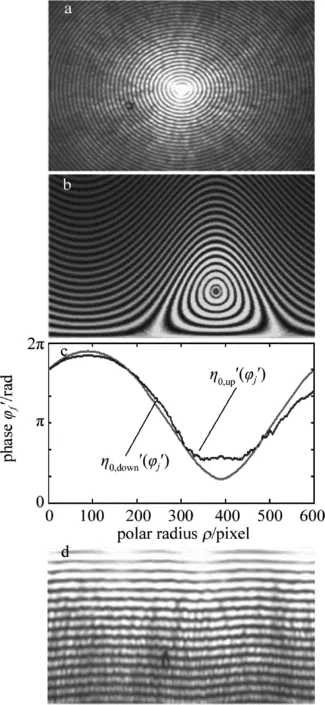
Fig.4 Calculation procedure of the phase scanning centering

a—theoriginphotographofnon-diffractingbeamf(x,y)b—thef(x,y)polartransformtof(ρ,φf)inposition(xc″,yc″)farawayfromidealcentrec—thedistributionofphaseη0′(φj′)alongpolarangled—thenon-diffractingimagewastransformedtopolarcoordinateinpositionofcommoncentre(xc,n,yc,n)

(7)重复步骤(3)～步骤(6)通过多次迭代寻找ν(xc′,yc′)在最小值时的坐标位置。

图4a中显示了在实际工程应用中捕获的无衍射光斑图像，因受多重因素干扰，在根据灰度重心法计算的初始中心坐标，存在偏离理论中心多个周期之外的可能，而极坐标系下的无衍射光斑灰度图在小极径区域纹理的不再是波浪条纹而是呈椭圆形亮斑状，如图4b所示，相应的其相位信息也遭受到破坏，然而在较大极径区域保持完好，如图4c所示。

故此，在迭代搜索计算中心初期，可按照上述步骤选择极径较大的图像少量无衍射光斑图像数据进行计算，获得初始较为准确的光斑中心坐标(在无衍射光斑零级环内)；再由步骤(1)～步骤(6)将整幅图像数据计算获得最终的中心坐标，此时极坐标变换后的图像，见图4d。这样不但减少了计算耗费，消除了对初始坐标的依赖；还实现对受噪声干扰的图像中心区域自动识别与剥离，以保证定中的计算精度。

3 算法的数字验证

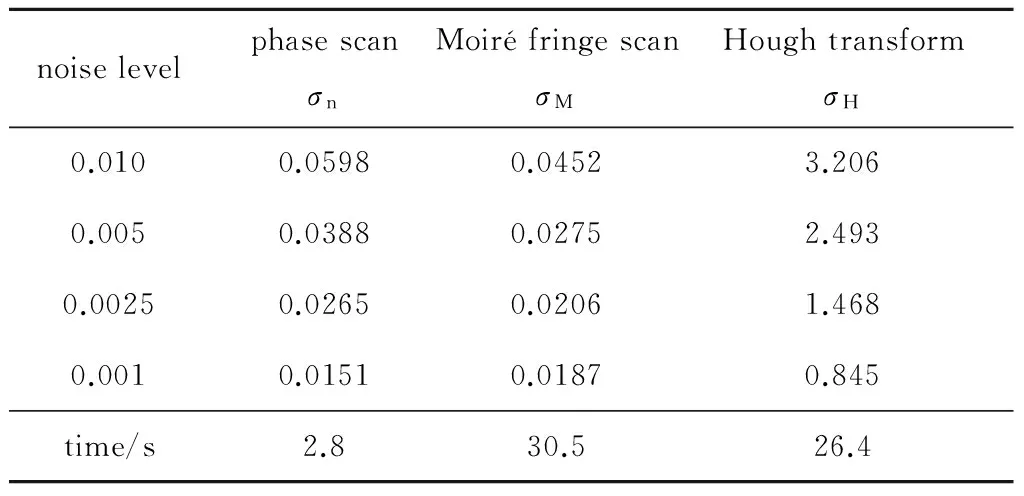
为了测试本文中所提出定中算法的有效性，首先由程序合成一幅理论中心已知的理想无衍射光图片；再添加不同的噪声水平，并分别采用本文中所提出的算法与数值莫尔条纹扫描定中算法、Hough圆检测算法进行模拟测试计算并对比。在对上述测试实验中，基于MATLAB软件平台下完成的，图片像素尺寸为200×200，采用函数imnosie添加各种噪声水平，对图像灰度分布在0～1在0.01的均方噪声下，对无衍射光斑图像影响是相当严重的，如图5所示，图中δ表示高斯噪声的方差，其计算结果如表1所示。

表1中，σn,σM和σH分别为相位扫描法、莫尔条纹扫描定中算法和Hough变换定中位置与理论中心的偏离量。

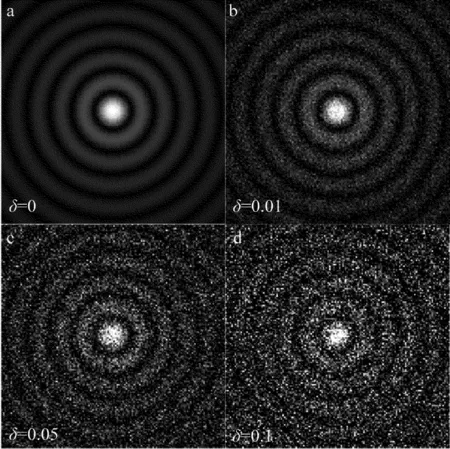
Fig.5Theidealnon-diffractionimagesunderdifferentnoiselevels,wheretheδrepresentsthevarianceofwhitenoise

Table 1 Numerical simulation of different algorithms under different noise

noiselevelphasescanσnMoiréfringescanσMHoughtransformσH0.0100.05980.04523.2060.0050.03880.02752.4930.00250.02650.02061.4680.0010.01510.01870.845time/s2.830.526.4

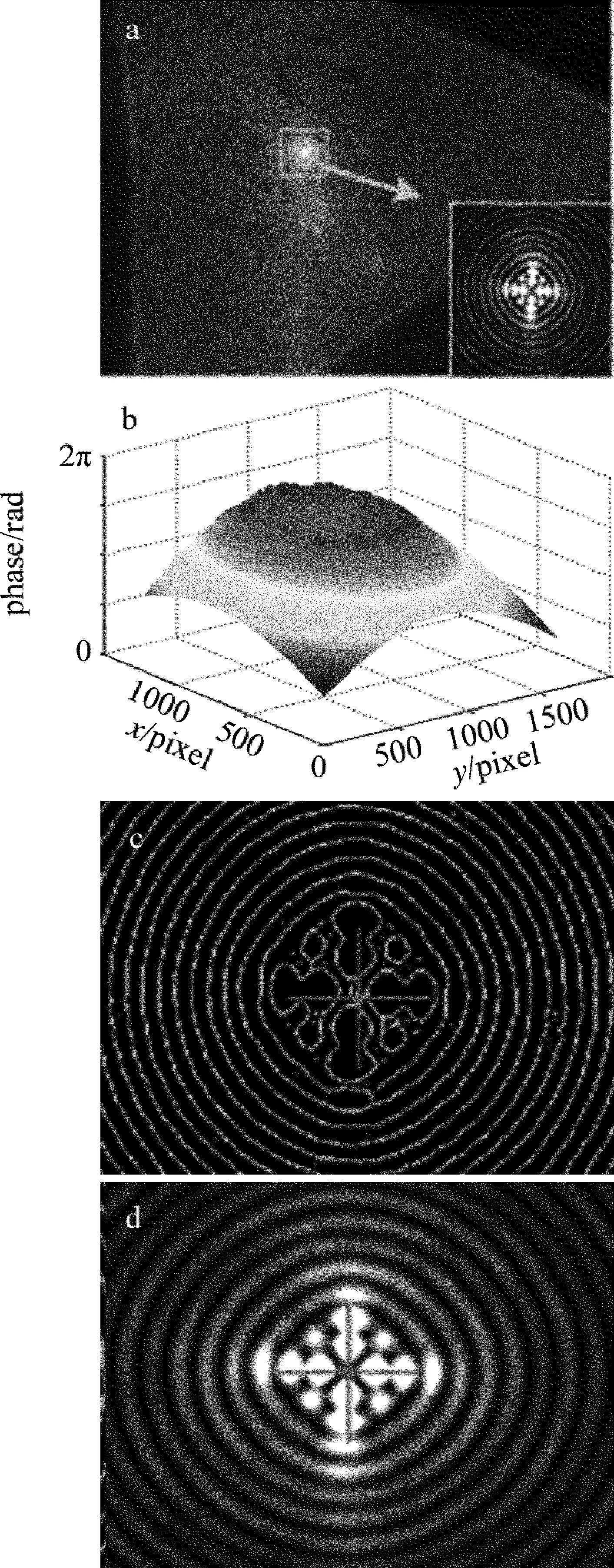
Fig.6 The centering results for non-diffraction images with complex background noise with different methods

a—the non-diffracting image was effected by background noise b—the cone of phase for origin non-diffracting image through digital Moiré fringe-scanning method c—the center position was obtained through traditional Hough transformation d—through polar transformation based phase-scanning method

计算结果表明，本文中所提出的定中算法在同等噪声水平的情况下具有稳定的亚像素定中计算水平，鲁棒性与计算时间优于Hough变换；较抗噪能力与精度与莫尔条纹扫描定中算法相当，但计算时间大大降低。

实际工程应用中的无衍射光斑图像，不是简单噪声叠加，axicon锥面表面形貌的加工质量、光照过饱和、倾斜入射、光束反射等综合因素引起的复杂背景下的无衍射光斑图像，如图6a所示。为了进一步检测算法，采用上述3种算法对多张类似图6a包含无衍射光斑纹理特征的复杂背景图像进行了计算，其中图6b～图6d分别为莫尔条纹扫描定中算法下的相位锥、边界提取并进行Hough圆变换定中算法下的计算中心与本文中所提出的极坐标变换下相位扫描定中计算下的中心。尽管无法得知实际中无衍射光斑的理论中心，但是将计算结果与肉眼对无衍射光斑同心环形纹理的观测中心对比，发现本文中所提出的基于极坐标变换的相位扫描定中算法明显地更靠近目测的中心。

4 结 论

所提出的基于极坐标变换的相位扫描定中算法运算量小、速度快，自适应中心区域纹理特征不规则的图像定中，能有效适应于复杂的背景下无衍射光斑的定中计算(譬如基于无衍射光斑的超场距离的直线度测量)，为无衍射光斑作为空间直线基准在实际的应用中提供一种新的有效的定中方法。

[1] FAN K C, ZHAO Y. A laser straightness measurement system using optical fiber and modulation techniques [J]. International Journal of Machine Tools and Manufacture,2000,40(14): 2073-2081.

[2] LIN S T. A laser interferometer for measuring straightness [J]. Optics and Laser Technology,2001,33(3): 195-199.

[3] SHERRINGTON I, SMITH E H. The significance of surface topography in engineering [J]. Precision Engineering, 1986,8(2):79-86.

[4] MA G L, ZHAO B, FAN Y Y. Non-diffracting beam based probe technology for measuring coordinates of hidden parts [J]. Optics and Lasers in Engineering, 2012,51(5): 585-591.

[5] ZHANG X B, ZHAO B, LI Zh. Measurement method of spatial straightness error using non-diffracting technology and moiré-fringe technology [J]. Journal of Optics,2004,A6(1):121-126.

[6] LI Zh W, WANG C J, SHI Y Sh. An algorithm for detecting center of structured light stripe combining gradient sharpening with barycenter method [J]. Journal of Image and Graphics,2008,13(1):64-68(in Chinese).

[7] YUEN Sh Y, MA Ch H. An investigation of the nature of parameterization for the Hough transforms [J]. Pattern Recognition, 1997,30(6):1009-1040.

[8] KONG B, WANG Zh, TAN Y Sh. Algorithm of laser spot detection based on circle fitting[J].Infrared and Laser Engineering,2002,31(3):275-279(in Chinese).

[9] ZHAO B.Digital Moiré fringe-scanning method for centering a circular fringe image [J]. Applied Optics, 2004, 43(14):2833-2839.

[10] BI X W, ZHU L M, ZHAO B. A center detection algorithm of non-diffracting beam based on ring filtering [J]. Journal of Shanghai Jiaotong University,2010,44(1):106-110(in Chinese).

[11] ZHAO B, LI Zh. Diffraction property of an axicon in oblique illumination [J]. Applied Optics, 1998, 37(13): 2563-2568.

[12] ZHOU L P, ZHAO B, LI Zh. Influence of manufacture error of an axicon on beam transmission [J]. Journal of Huazhong University of Science and Technology,2001,29(3):61-63(in Chinese).

[13] ZHANG H Zh, YAO M, LEI P,etal.Research of image processing method of far-field laser spots[J]. Laser Technology, 2013, 37(4):460-463(in Chinese).

Phase scanning centering based on polar coordinate transformation

MAGuolu,ZHAOBin

(School of Mechanical Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

In order to realize fast and precise centering with non-diffracting spot as straight-line datum under complex background noise, the fluctuation of phase angle of non-diffraction spot with polar angle under polar coordinates was obtained with the phase scanning method. The deviation was the difference between the phase of non-diffraction spots on the ring direction and the phase of standard sinusoidal stripes. Finally, the centering of the non-diffraction spot can be realized after a number of iterations. Theoretical analysis and experimental verification show the method has the good ability of anti-noise, less time consumption and sub-pixel level accuracy.

image processing; signal processing; diffraction; phase scanning; non-diffraction spot

1001-3806(2014)04-0449-06

国家九七三重点基础研究发展计划资助项目(2013CB035405)

马国鹭(1981-)，男，博士研究生，主要从事精密测量方面的研究。

*通讯联系人。E-mail: zhaobin63@sohu.com

2013-09-04；

2013-10-10

TN911.73

A

10.7510/jgjs.issn.1001-3806.2014.04.004