N个并联耦合线圈的等效自感公式*

周国全

(武汉大学物理科学与技术学院 湖北 武汉 430072)

相互耦合的并联与串联线圈的等效自感问题，是电磁学与电工学研究中有关电磁感应与耦合线圈的重要内容之一[1～4]．相互没有耦合的并联线圈的等效自感系数可通过交流电的复阻抗的并联公式简单计算．在N个线圈串联耦合情形，其等效自感系数可用磁场等效储能法简单求出，目前文献中已有关于N=2情形的结论,并可很容易地推广到N>2情形[1～4]；在并联耦合情形，文献[3～5]给出了无直流内阻的两个自感线圈并联耦合时的等效自感公式

(1)

其中L1，L2为两线圈的自感系数,M为两线圈的互感系数．文献[3～5]还讨论了两个有直流内阻的自感线圈并联耦合的等效去偶电路及其等效自感问题．在多个线圈之间自感与互感交叉并存的情形，我们无法通过业经解决的两耦合并联线圈的已有结论加以归纳推理．

本文基于电磁感应的基本原理，运用线性代数中高阶矩阵与行列式的若干技巧，和齐次线性微分方程组的非平庸解的存在性条件，成功地推导出N个相互耦合、无直流内阻的并联线圈的等效自感系数，即由它们的自感与互感系数构成的两个分别为N阶与N-1阶的矩阵的行列式之比；给出了存在反向耦合情形的符号规则；并对若干特例情形进行了具体计算，所得结论也与文献已有结果相符．对其特例的研究表明，相互之间完全没有耦合的N个并联线圈的等效自感系数,与通过交流电的复阻抗的并联公式求出的结果相符；而对完全耦合这一极限情形，本文也分类做了分析与讨论．

1 N个并联耦合线圈的等效自感系数的一个定理

由于第i，j两个线圈之间的互感系数是满足所谓Neumann关系:Mij=Mji, 出于理论推导与数学表达的简洁、紧凑与对称性的考虑，可将第i个线圈的自感系数Li重新标记为Li≡Mii，i=1,2,…,N, 即自感系数亦可理解为一个线圈自己对自己的互感．于是有如下定理:

(2)

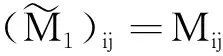
(3)

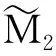
(i,j=1,2,…,N-1)

(4)

兹证明如下：如图1所示是N=3时的示意图, 运用法拉第电磁感应定律，根据并联耦合电路的总感应电动势ε(t)与各支路感应电动势εi(t)、瞬时总电流与瞬时支路电流Ii(t)的关系，忽略各线圈的直流内阻，考虑自感与互感同时存在的一般情形，并设Le代表N个并联耦合线圈的等效自感系数，有如下等式

图1 并联耦合感应线圈示意图

ε(t)=ε1(t)=ε2(t)=…=

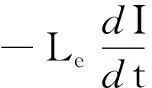
(5)

I(t)=I1(t)+I2(t)+…IN(t)

(6)

(7a)

(7b)

………

(7c)

根据式(5)、(6)，方程组7(a)～7(c)即如下矩阵形式

(8)

这个N元一阶齐次线性微分方程组又可表述为如下矩阵形式

(8b)

注意式(8)与式(8a)、(8b)中的系数矩阵是一个实对称矩阵，这是因为其中Mij=Mji,Mii=Li,i,j=1,2,…,N．根据N元一阶齐次线性微分方程组的非平庸解的存在性条件，如果对任意的时变电流(如任意频率的交流电)，方程组(8)与(8a)、(8b)均有非平庸解(平庸解即对应于直流稳恒情形，各导数为零)，则其系数矩阵的行列式必定为零

(9)

这一方程表观上是Le的一元N次方程，难以求解．实际上研究发现，它只是Le的一元一次方程．运用行列式的性质，将式(9)左边第2，3，…，N行减去第一行，其值不变，即得式(10)

(10)

再运用行列式的行加法性质，将上式左边按第一行拆分为两项之差，并移项，提取右边行列式第一行的公因子Le，可得式(11)

(11)

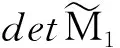
(12)

将式(11)右侧行列式的第2，3，…，N列减去第1列, 其值不变，再按第一行余子式展开, 即得如下N-1阶行列式

(13)

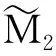
(14)

2 存在反向耦合情形的符号规则

在用基尔霍夫回路定理处理存在互感的交流回路时, 应遵守同名端规则[1～4 ]．如图2所示，在计算存在反向耦合的并联感应线圈的等效自感系数时，我们面对同样的复杂问题．

图2 反向并联耦合线圈

基于如下两个基本事实: 即两个顺向(反向)耦合的并联载流线圈的互感储能为正(负)的，以及无论两线圈是顺向或反向耦合，每个载流感应线圈的自感储能均为正值，可以推断公式(2)与矩阵(3)、(4)中线圈之间的互感项的符号取法，即应落脚于互感项相对于其自感项的符号的比较而定，正像N个耦合载流线圈的磁场储能公式一样，有

(15a)

其中Ii是第i个线圈的电流．我们可在每个自感与互感系数前添加一符号因子εij=±1，据此将磁场储能公式(15a)改写为

(15b)

比较(15a)、(15b)两式，可对矩阵(3)、(4)的元素订立如下符号规则

亦即εii=1

(16a)

(16b)

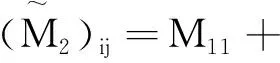
εi+1,1Mi+1,1-ε1,j+1M1,j+1i,j=1,2,…,N

(16c)

3 N=2, 3时的若干特例情形的具体结论

M11M22-M12M21=L1L2-M2

(17)

(18)

将(17)、(18)二式代入公式(2)可得式(1)，正是文献[3～5]所给的已知结果, 表明我们所推导的公式(2)对两个线圈的并联耦合情形是正确无误的．在两个线圈反向耦合时，如图2所示，按本文第三部分的符号规则，可知

(19)

即得反向耦合的并联感应线圈的等效自感系数表达式[3～5 ]

(20)

当N=3时，即对3个耦合的并联感应线圈，有

M11M22M33+M12M23M31+M21M32M13

-M32M23M11-M31M22M13-M21M12M33=

(21)

L1+M32-M21-M31L1+M23-M12-M13

(22)

再将式(21)、(22)代入公式(2)，即得3个顺向耦合的并联线圈的等效自感系数的计算公式．

4 完全不耦合的并联线圈的等效自感系数

当N个线圈并联但完全不耦合时，(仅限于顺向并联情形)，即Mij=Mji=0，(i,j=1,2,…,N，且i≠j)，此时并联线圈的等效自感系数由

(23)

+L1L2…LN-2LN+L1L2…LN-1=

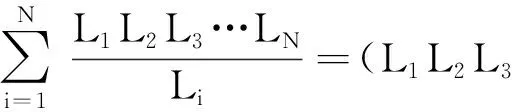
(24)

(25a)

即得

(25b)

这显然与用交流电的复阻抗的并联公式计算去耦(Decoupled)并联感应线圈的等效复阻抗的结果是彼此一致的，再一次证明我们所得公式(2)的正确性与有效性．

5 全同对称的并联耦合情形的等效自感系数

所谓全同对称的并联耦合情形，即

L1=L2=…=Ln≡L

Mij=Mji=M(i,j=1,2,…，N)

但L≠M的情形，此时，有

[L+(N-1)M](L-M)N-1

(26)

(27)

(28)

计算出(26)与(27)式中行列式的结果是需要一定的数学技术的．它们可化成两个递推数列之通项的求解问题．限于篇幅，我们将它们留给读者自己完成．在N=2时，按式(28)，有

(29)

这显然也与用公式(1)在全同对称情形的化简结果彼此一致．

再如N=3时

(30)

(31)

故有

(32)

这再次表明我们所得公式(2)与 (28)的正确性与有效性．

6 完全耦合的并联线圈的等效自感的一点讨论

文献[1～6 ]等均指出或证明两个线圈之间若完全耦合, 则其互感系数必为彼此自感系数的比例中项．即

Li≡LMij=Mji=M(i,j=1,2,…N)

Le=L=L1=L2=…=LN

(33)

7 结论与前瞻

在最一般的情形，耦合线圈之间可以是既有并联又有串联的混合联接方式．任意N个串联且相互耦合的线圈的等效自感系数可通过磁能等效法简单求出，[参考式(15a)、(15b)]，且同样可通过本文给定的符号规则来解决存在反向耦合的等效自感问题．本文的定理[公式(2)]成功解决了N个并联且相互耦合线圈的等效自感问题，其对各种特例情形的具体结论，均与文献中已有的结果相符，检验和证实了理论的正确性．这为进一步处理混联且相互耦合的线圈的等效自感问题奠定了理论基础，并将有益于电磁场、电路分析及电工学的教学与研究．

参考文献

1 贾起民，郑永令，陈暨耀. 电磁学.北京：高等教育出版社，2001, 223～230

2 胡友秋，程福臻，刘之景.电磁学.北京： 高等教育出版社，1994.319～324

3 Charles K Alexander;Matthew N.O.Sadiku.Funda-

mentals of Electric Circuits,the McGraw-Hill Companies.Inc.2000,(First Edition),528～530,535～537,569～571

4 刘南平, 齐兆艺. 电路基础. 北京: 科学出版社, 2005.

148～151

5 史祥蓉、杨绍华.并联线圈的等效自感和电流分配问题的讨论. 大学物理，2010, 29 (1):31～35

6 刘佑昌.关于互感系数M的讨论.物理与工程，1995, 5(2):6～8