一种基于多元探测器阵列的分块图像压缩传感算法

张智诠,丁晟,2,金伟其

(1.装甲兵工程学院控制工程系,北京 100072;2.73021部队,浙江杭州 310023; 3.北京理工大学光电成像技术与系统教育部重点实验室,北京 100081）

一种基于多元探测器阵列的分块图像压缩传感算法

张智诠1,丁晟1,2,金伟其3

(1.装甲兵工程学院控制工程系,北京 100072;2.73021部队,浙江杭州 310023; 3.北京理工大学光电成像技术与系统教育部重点实验室,北京 100081）

针对压缩传感理论应用于单元探测成像时图像重构时间随图像尺寸增大而迅速增大的问题,提出了一种利用数字微镜和多元探测器进行编码测量,利用最小全变分法进行图像重构的分块图像压缩传感算法,并对重构分块图像进行灰度拉伸,提高了图像的峰值信噪比和结构相似度。仿真实验结果表明:算法具有计算时间短、重构图像质量高的特点,对于16图像分块,至少可缩短40%重构时间;通过分块图像灰度拉伸,重构图像的峰值信噪比和平均结构相似度较不拉伸时分别提高70%和11%.文中算法为高分辨压缩成像的应用研究提供了一种有效的技术参考。

信息处理技术;压缩传感;图像稀疏与重构;多元探测器;平方约束最小全变分法;等式约束最小全变分法

0 引言

由于压缩传感[1](CS)能在采样过程中实现数据压缩,大大降低了数据存储和传输的代价,因而受到人们的广泛关注,并在单像素压缩成像[2]、编码孔径成像[3]、光谱成像[4]中得到应用。随着探测器技术的发展,多元探测器阵列被广泛应用于可见光和红外热成像领域,对大阵列图像压缩传感的需求会越来越多。但CS理论在对大尺寸图像应用时,存在压缩采样和重构时间过长、存储量过大,甚至出现超出计算机内存限制的问题。

本文利用CS理论探讨一种基于数字微镜(DMD)和多元探测器的分块图像CS成像方法,探讨DMD的光调制分布形式、微镜数量与光电探测器、信号采集A/D转换精度的关系,旨在提高压缩成像的性能,获得更高分辨率的图像,推进CS理论对实际光学成像系统的应用。

1 CS理论及算法

为了保持信号的完整性,传统的信号采集频率必须大于或等于奈奎斯特频率,而CS理论利用信号在某些变换域下呈现的稀疏性(即大部分信号为0或接近于0),实现信号采样的同时完成信号的压缩。当然,为了由压缩测量值获得原图像,还需要经过重构计算。

设x为二维图像信号,Φ为测量矩阵,Ψ为稀疏基,CS理论用矩阵可表示为[1]

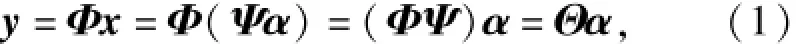
式中:y为测量值,其维度小于图像x;Θ=ΦΨ为传感矩阵。图1为(1)式的矩阵图形表示。

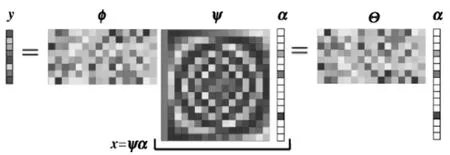
图1 CS过程示意图Fig.1 Schematic diagram of CS progress

为了由(1)式精确重构图像信号,要求传感矩阵Θ满足约束等距性条件(RIP)[5],或等价为测量矩阵Φ和稀疏基Ψ不相关(即Φ的行和Ψ的列不相关)。

由于线性方程组y=Θα是欠定的,需增加约束条件缩小解的范围。例如,采用正则化方法[6],由罚函数J(x)对所有x进行估计,获得使J(x)最小的解x,即将重构过程转化为求解最优化问题

考虑到实际场景辐射和光学系统成像的特点,本文采用在时域中测量、在变换域中稀疏的最优化模型[7]

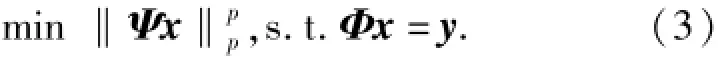
时域中的图像信号x经过稀疏基Ψ变换,在变换域下可等价表示为α,

式中:Ψ†为Ψ的逆变换矩阵。(3)式的解Ψ^x是图像x在变换域下的等价表示:

最后,经逆变换Ψ†即可求得时域下的重构图像

由上可以看出,图像重构就是从低维测量数据y精确或近似精确地恢复出原始高维图像^x.现有图像重构算法大致分为基于l1范数最小化的凸优化算法和贪婪算法两类[8-11]。研究表明,基于最小全变分(Min-TV)的图像重构方法可以获得较好的图像质量[12]。Min-TV法依据约束条件不同分为平方约束最小全变分(TVQC)法、等式约束最小全变分(TVEQ)法及丹齐格Min-TV法等。

2 图像分块CS算法

单像素CS相机[13]利用DMD对场景调制,每改变一次微镜0-1排列形式,光电二极管输出一个测量值,经多次测量后,利用Min-TV算法重构原始图像。其优点是只需一个光电探测器,信号处理电路较为简单,但测量次数较多,特别是当DMD微镜数量(即图像像素数)较多时,对探测器的灵敏度和响应速度要求较高,且重构计算时间较长。

2.1 多元探测器压缩成像

如图2所示,本文利用多元探测器阵列替代单像素探测器,将DMD反射后的场景辐射,由多元探测器阵列进行压缩采样,然后通过适当的优化方法进行图像重构。这样不仅降低了对探测器灵敏度和响应速度的要求,而且缩短了图像重构时间。

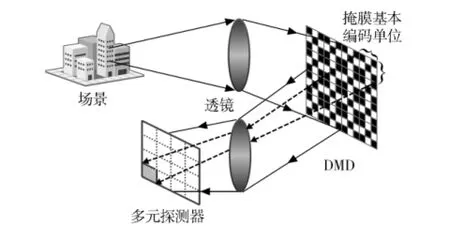
图2 采用DMD的多元探测器高分辨成像系统示意图Fig.2 Schematic diagram of high-resolution imaging systembased on multi-element detector with DMD

2.2 编码测量

图3是用DMD形成的某一编码掩膜形式,其只包含1和0两种元素,分别对应微镜不同的反射状态,当反射的场景辐射被探测器接收时,掩膜值为1,反之为0.一个掩膜基本编码单位包含多个微镜。

图3 用DMD形成的某一编码掩膜形式Fig.3 Coded mask pattern formed by DMD

设多元探测器阵列的光敏元数为N×N,fi,j为投射到第i个基本编码单位中第j个微镜上的光强, yi为第i个探测器输出的测量值,则掩膜编码测量过程可表示为

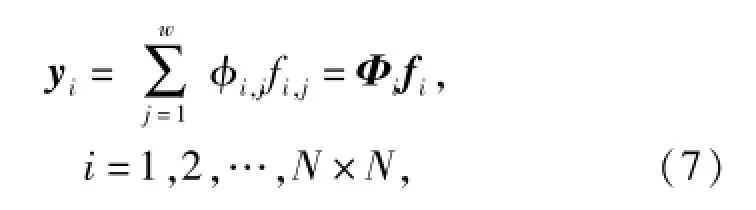
式中:φi,j为Φ的矩阵单元;w为基本编码单位内的微镜数;乘积φi,jfi,j在第i个基本编码单位内进行。

由(7)式知,若重构图像为8位灰度,即投射到掩膜每一微镜上的光强fi,j最大值也为8位二进制,则测量值yi的最大值为log2(w×fi,j)位二进制。例如,w=8×8,则yi的最大值为14位二进制,即当基本编码单位内的微镜数为64时,若重构图像为8位灰度,则要求A/D的转换精度为14位二进制。

由于基本编码单位的一种形式(如图3所示)只能获得一次测量值yi,要重构图像x,就需要不断改变基本编码的形式,进行多次压缩采样。考虑到DMD实现的可能性,本文采用0-1高斯随机矩阵[14]作为掩膜基本形式。

上述多元探测器阵列压缩成像过程可理解为是N×N个单元探测器成像的组合,且每个探测单元只接收一个基本编码单位反射的辐射能量。

由图2可知,重构图像的分辨率由DMD的微镜数量决定,而不是由探测器光敏元的数量决定。若增加DMD的微镜数量,就能有效提高多元探测器成像的分辨率。

2.3 稀疏与重构

由调和分析理论知,图像x可表示为某组基函数{ψk}的线性组合:

(8)式中的非零系数项αk越少,图像就越稀疏,即在变换Ψ下,可用较少的数据近似表示原图像x.本文选用一维离散傅里叶变换(DFT)作为图像x的稀疏变换。

综合考虑TV法重构图像,特别是对实际景物图像重构的性能,本文分别采用TVQC和TVEQ进行图像重构。

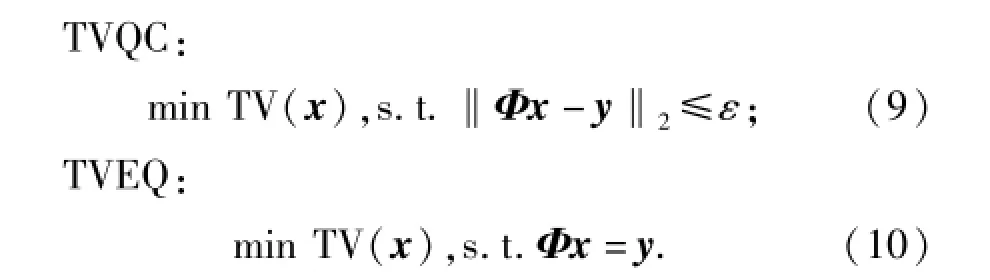
由于(9)式、(10)式是典型的二阶圆锥规划(SOCPs)问题,本文采用对数障碍法(LBA)[12]求解。

2.4 图像分块CS算法

(7)式～(10)式即为对整幅图像进行CS成像的数学描述,为了考查上述算法重构图像的质量,本文以图4(a)(256×256像素的8位灰度图像baboon)为例进行仿真计算。图4(b)和图4(c)分别为采用(7)式～(10)式对图4(a)进行编码测量(测量次数为总像素数的50%,即采样率)和重构(LBA法)的图像,其计算时间、峰值信噪比PSNR和平均结构相似度MSSIM列于表1、表2中的第2列。

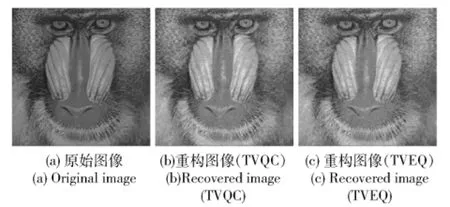
图4 baboon整体图像数值重构结果Fig.4 The reconstructed results of baboon image

针对CS算法对大尺寸图像整体重构耗时较长的问题,本文提出一种对实际成像范围进行分块的CS算法,即通过分块,减小单次图像重构的规模,也减少了计算时间,其主要步骤如下:

1)按多元探测器的光敏元数N×N对成像范围进行分块,并将第k个成像子块(其像素数为n)展为列向量形式xk(xk∈Rn×1,k=1,2,…,N×N).

2)对每一子块进行步骤3～步骤6的测量与重构操作,并遍及整个图像。

3)用与第k个子块对应的掩膜基本编码单位形成的测量矩阵Φk∈Rm×n(m≪n)对子图像列向量xk进行压缩采样,得到测量值yk(yk∈Rm×1).

4)选择DFT为稀疏基Ψ,由(4)式有

式中:传感矩阵~Θk是由测量矩阵Φk和稀疏基Ψ的逆变换矩阵Ψ†组成的复合矩阵。

对第k个子块,(9)式和(10)式可写为

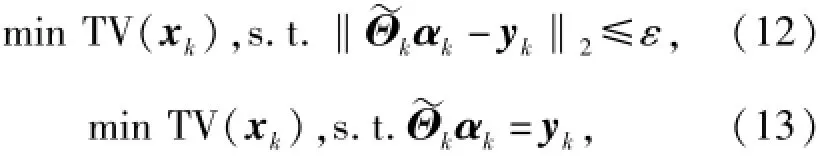
式中:αk(αk∈Rn×1)是子图像列向量xk在Ψ下的稀疏表示。

5)对第k个子块,(12)式和(13)式中的全变分TV(xk)定义为灰度梯度幅值之和:

式中:Dh;ijxk和Dv;ijxk分别为第k个子图像灰度的水平差分和垂直差分。引入TV(x)的上界t= (tij)并使其最小化,则(12)式、(13)式转化为SOCPs问题

6)利用牛顿迭代法求解(18)式或(19)式。其主要思想是[12]:当障碍参数τ→［时,(18)式或(19)式的极小解t(τ)趋向于最优解^t,对应的^αk即为该式的最优解。迭代过程中,若第p次迭代(对应的障碍参数为τp)的对偶间隙m/τp满足精度要求: m/τp＜η,则停止迭代,且^αk即为所求的最优解;若不满足要求,则继续新的迭代计算,直至满足要求或达到最大迭代次数,停止迭代。

3 仿真计算

为了检验本文提出的分块CS算法的有效性,分析图像分块数与图像重构质量和计算效率的关系,对图4(a)进行4、16、64和256分块,然后对每一子块进行编码测量(采样率为50%)和LBA法重构,并用PSNR及MSSIM评价重构图像质量[15]。

以下采用Matlab 2008,在Intel Core I3,CPU 3.30 GHz,内存4 GB的台式机上进行仿真计算。

3.1 TVQC重构分块图像计算

表1和图5为TVQC重构分块图像的计算结果和重构图像。

表1 图5的TVQC重构计算结果Tab.1 The results in Fig.5 reconstructed via TVQC

图5 TVQC模型对图4(a)进行不同分块的重构图像Fig.5 Baboon images in different blocking modes in Fig.4(a)reconstructed via TVQC

由于TVQC重构图像时,需对分块图像进行归一化和均值平移,故重构后拼接图像时无参考灰度,本文采用对每一子块进行0～255拉伸显示。

3.2 TVEQ重构分块图像计算

表2和图6为TVEQ重构分块图像的计算结果和重构图像。

由图5和图6可看出:1)图像分块相同时,两种方法计算的PSNR和MSSIM值较为接近,但TVEQ的计算时间比TVQC分别多28.2%、34.4%、40.7%、50.5%和63.0%.2)图像16分块时,计算时间最短。3)随着分块数增加,分块间的灰度差异增大,“马赛克”现象越来越明显,图像可视性变差。

3.3 图像灰度拉伸方法

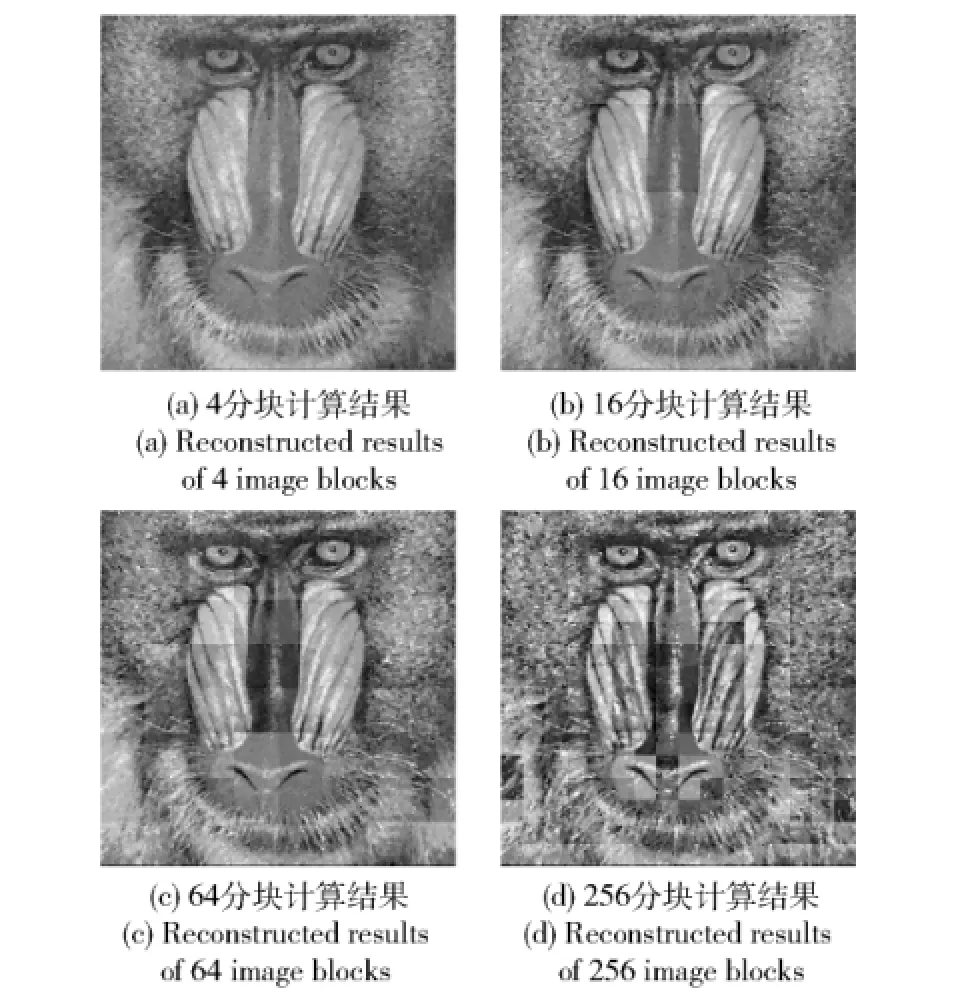
图6 TVEQ模型对图4(a)进行不同分块的重构图像Fig.6 Baboon images in different blocking modesin Fig.4(a)reconstructed via TVEQ

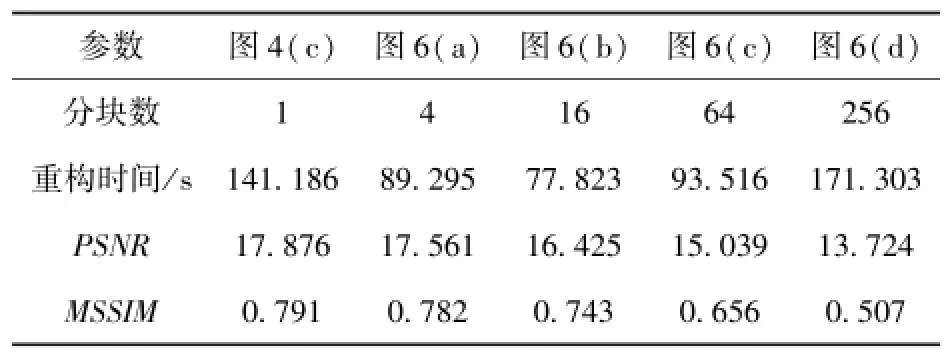
表2 图6的TVEQ重构计算结果Tab.2 The results of baboon images in Fig.6 reconstructed via TVEQ

针对重构子图像间的“马赛克”现象,本文进一步提出一种参考相邻子图像进行灰度拉伸的方法。如图7所示,首先选定基准块,并由基准块与相邻块邻域的平均灰度差对相邻块进行灰度拉伸,然后将拉伸后的块作为新的基准块,对次邻分块进行拉伸,直至整个图像。

基准块与相邻块邻域的平均灰度差定义为相邻边界两列(或两行)灰度差的平均值

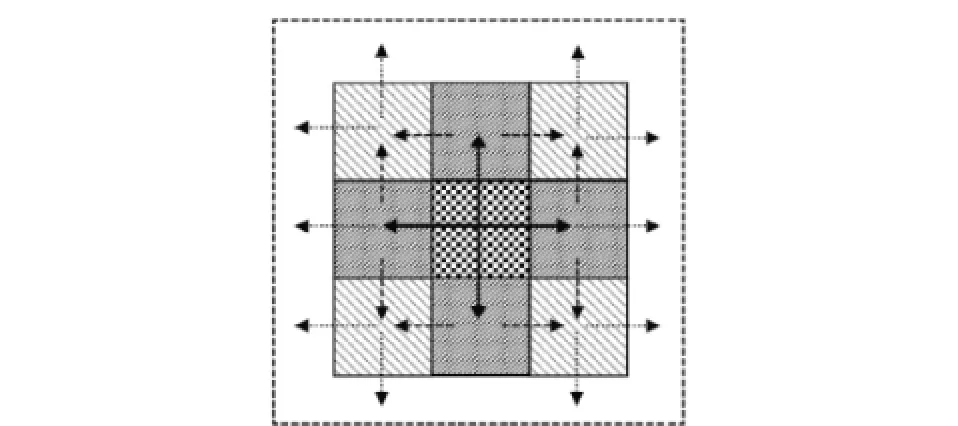
图7 参考分块图像邻域进行灰度拉伸示意图Fig.7 Schematic diagram of gray stretching

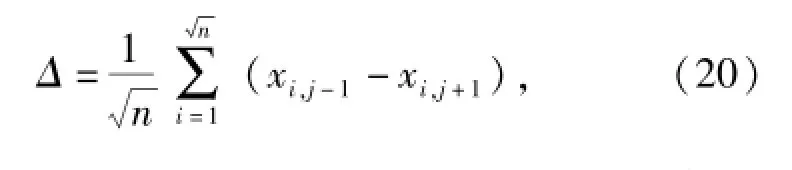
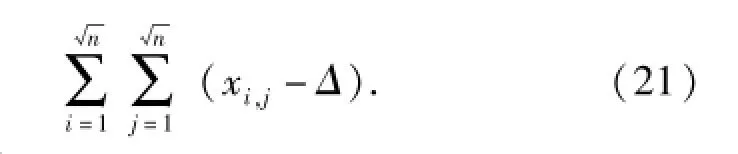
图8和图9分别为按TVEQ和TVQC重构,然后按(21)式灰度拉伸后的图像,表3和表4为相应的计算结果,其重构时间包含图像灰度拉伸时间。

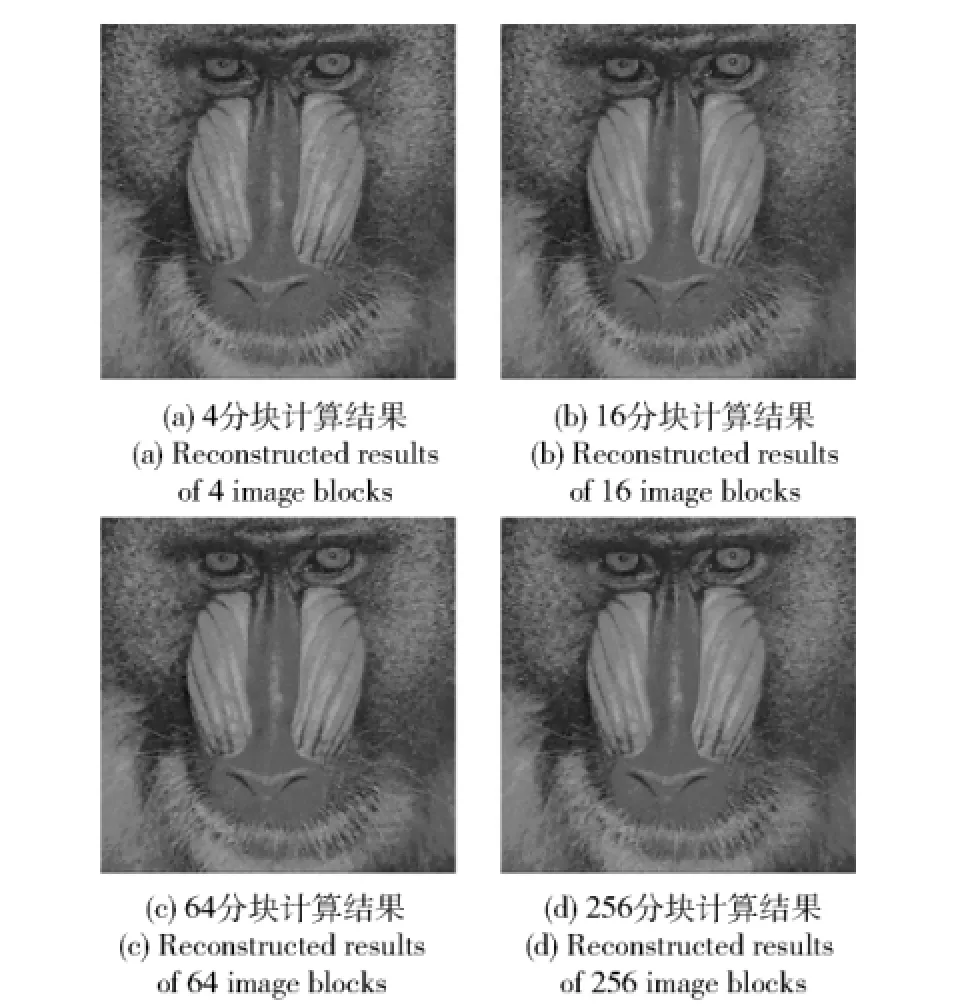
图8 经灰度拉伸后的重构图像(TVQC)Fig.8 The results of gray stretched baboon images reconstructed via TVQC

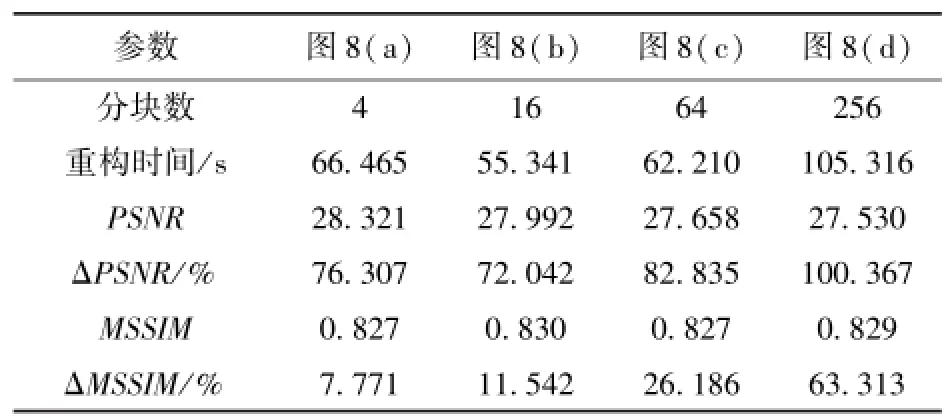
表3 图8经灰度拉伸的重构计算结果Tab.3 The results of gray stretched images in Fig.8 reconstructed via TVQC

由图8和图9可看出,经灰度拉伸后,“马赛克”现象基本消除,PSNR、MSSIM值相应增加,重构图像质量得到进一步提升。

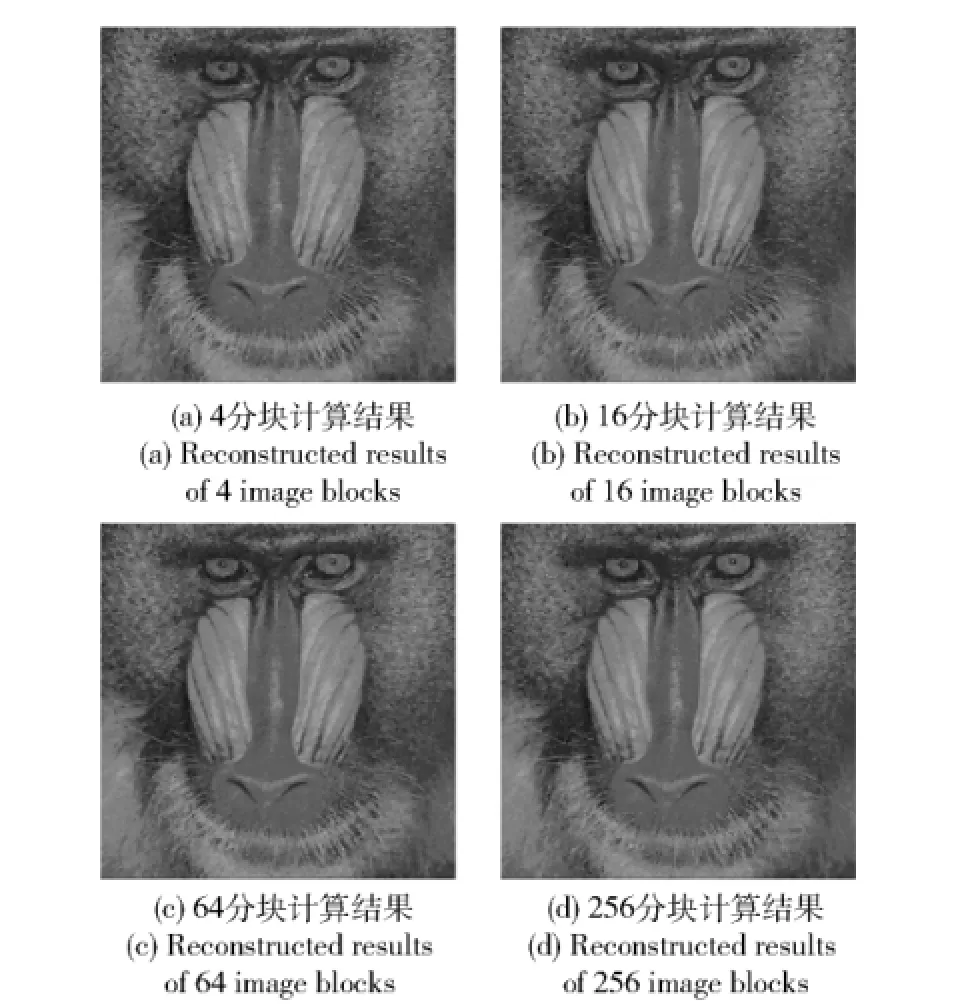
图9 经灰度拉伸后的重构图像(TVEQ)Fig.9 The results of gray stretched baboon imagesreconstructed via TVEQ

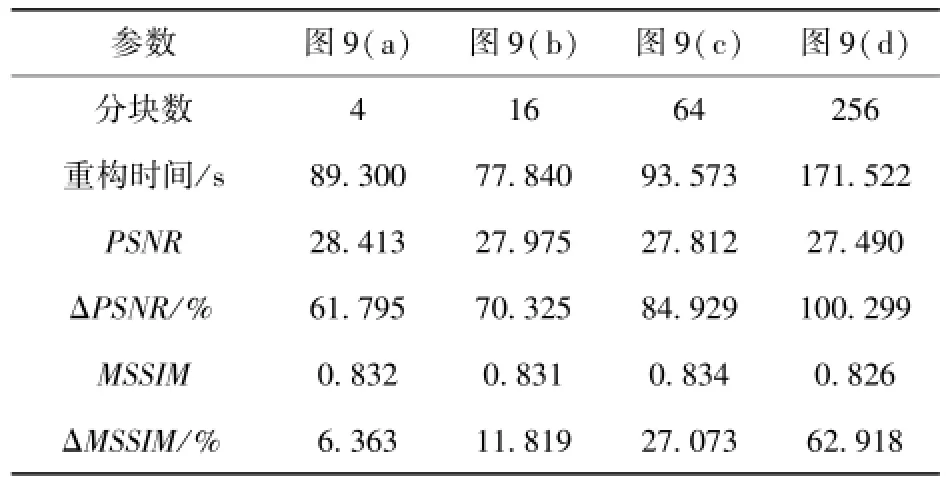
表4 图9经灰度拉伸的重构计算结果Tab.4 The results of gray stretched images in Fig.9reconstructed via TVEQ

3.4 其他参考图像的仿真计算

为了进一步验证上述算法的稳定性,本文还对256×256像素的8位灰度图像lena(见图10(a))和barbara(见图10(b))进行仿真计算。

表5～表8为按3.1～3.3节的图像分块方法进行编码测量、TVQC和TVEQ重构,以及图像灰度拉伸的重构计算结果。

图10 Lena和Barbara原始图像Fig.10 Lena and Barbara's original images

由表5～表8可以看出,图像Lena和Barbara的计算结果与Baboon的计算结果相仿,分块特性规律也一致,说明本文算法具有较好的有效性、稳定性和一致性。另外,由表1～表8还可看出,当分块数为16时,重构时间最短,且与图像内容无关。究其原因是因为重构中一部分计算与矩阵大小有关,而另一部分则与图像分块数有关,二者综合结果导致重构总时间的非线性,并在16分块时出现极小。

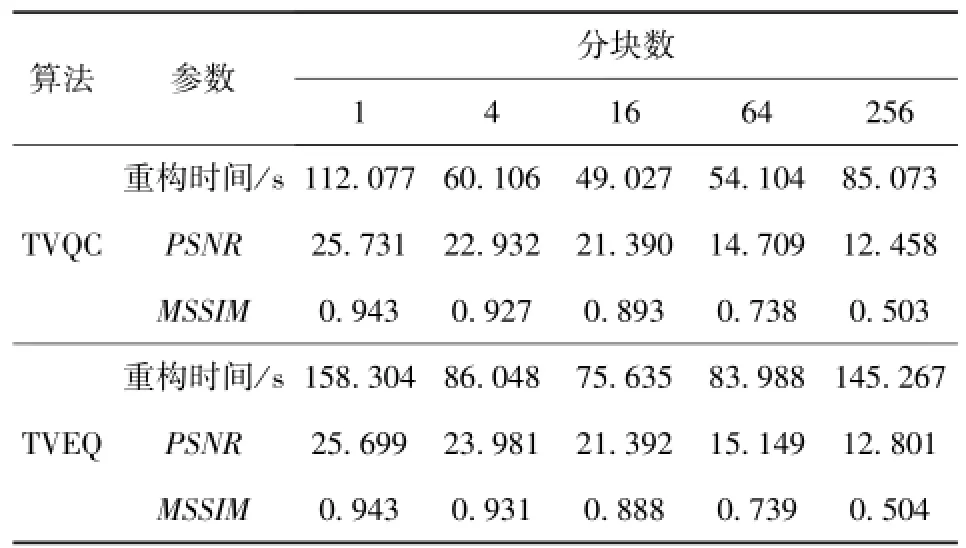
表5 Lena图像重构计算结果Tab.5 The reconstructed results of Lena's image

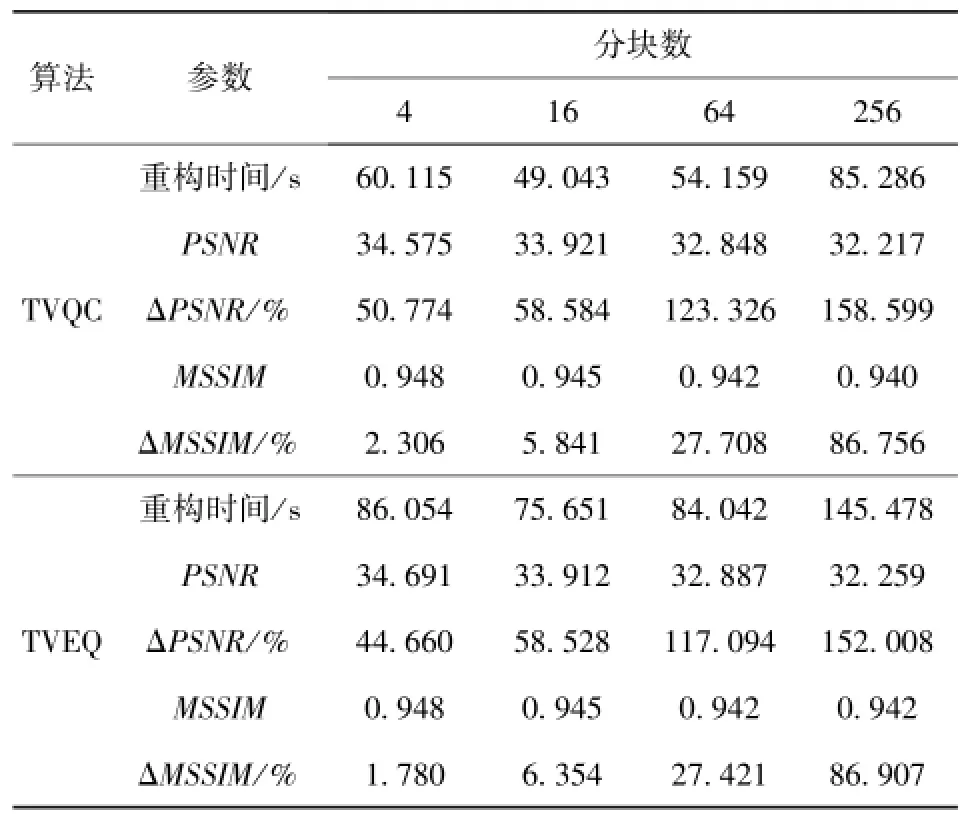
表6 Lena图像经灰度拉伸的重构计算结果Tab.6 The reconstructed results of gray stretchedLena's image

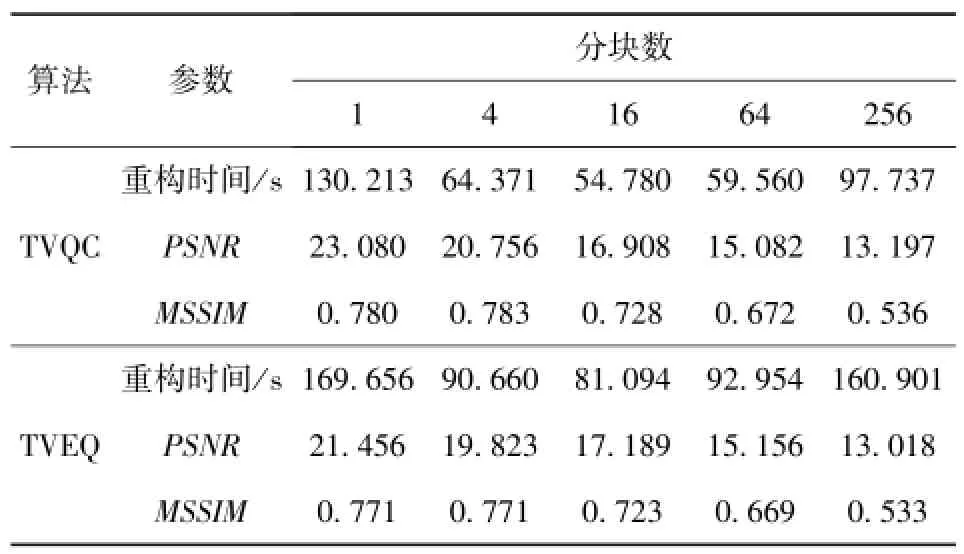
表7 Barbara图像重构计算结果Tab.7 The reconstructed results of Barbara's image

表8 Barbara图像经灰度拉伸的重构计算结果Tab.8 The reconstructed results of gray stretchedBarbara's image

4 结论

综上所述,本文提出的基于DMD和多元探测器阵列的分块CS成像算法,从实际光学系统的结构和特点出发,采用0-1高斯随机分布构成测量矩阵,通过DMD与多元探测器阵列组合实现光学系统在图像采集的同时完成图像的压缩,通过图像分块解决大阵列图像重构占用内存过大、重构时间过长的问题,为CS成像理论的实际应用提供了有益的技术参考。

仿真实验结果验证了本文算法对不同分块大小、不同场景图像进行编码测量和图像重构的稳定性和有效性,所提出的分块图像灰度拉伸方法,有效提高了重构图像的PSNR、MSSIM值和可视性。

另外,由仿真实验可看出,虽然TV法能高概率、高质量地恢复实际景物图像,但限于TV法的复杂性,其图像重构时间比其他方法长,因此,该算法适用于准静态实际景物的压缩成像、对后续图像重构时间要求不高的场合。

References)

[1] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1290-1305.

[2] 陈涛,李正炜,王建立,等.应用压缩传感理论的单像素相机成像系统[J].光学精密工程,2012,20(11):2523-2530.

CHEN Tao,LI Zheng-wei,WANG Jian-li,et al.Imaging system of single pixel camera based on compressed sensing[J].Optics and Precision Engineering,2012,20(11):2523-2530.(in Chinese)

[3] 肖龙龙,刘昆,韩大鹏,等.压缩感知理论在光学成像中的应用[J].应用光学,2012,33(1):71-77.

XIAO Long-long,LIU Kun,HAN Da-peng,et al.Application of compressed sensing in optical imaging[J].Journal of Applied Optics,2012,33(1):71-77.(in Chinese)

[4] 冯燕,贾应彪,曹宇明,等.高光谱图像压缩感知投影与复合正则重构[J].航空学报,2012,33(8):1465-1472.

FENG Yan,JIA Ying-biao,CAO Yu-ming,et al.Compressed sensing projection and compound regularizer reconstruction for hyperspectral images[J].Acta Aeronautica et Astronautica Sinica, 2012,33(8):1465-1472.(in Chinese)

[5] Candès E J,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2): 489-509.

[6] Elad M.Sparse and redundant representations:from theory to applications in signal and image processing[M].Berlin,Germany: Springer,2010.

[7] Dai Q,Sha W.The physics of compressive sensing and the gradient-based recovery algorithms[EB/OL].[2013-05-07].http:∥arxiv.org/abs/0906.1487.

[8] Tropp J A,Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.

[9] Needell D,Vershynin R.Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit [J].IEEE Journal of Selected Topics in Signal Processing,2010, 4(2):310-316.

[10] Do T T,Lu Gan,Nguyen N,et al.Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]∥42nd Asilomar Conference on Signals,Systems&Computers.California,US:IEEE,2008:581-587.

[11] Needell D,Tropp J A.CoSaMP:iterative signal recovery from incomplete and inaccurate samples[J].Applied and Computational Harmonic Analysis,2009,26(3):301-321.

[12] Candes E,Romberg J.l1-magic:recovery of sparse signals via convex programming[EB/OL].[2013-05-07].http:∥users. ece.gatech.edu/justin/l1magic/downloads/l1magic.pdf.

[13] Duarte M F,Davenport M A,Takhar D,et al.Single-pixel imaging via compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):83-91.

[14] Do T T,Lu Gan,Nguyen N H,et al.Fast and efficient compressive sensing using structurally random matrices[J].IEEE Transactions on Signal Processing,2012,60(1):139-154.

[15] 佟雨兵,张其善,祁云平.基于PSNR与SSIM联合的图像质量评价模型[J].中国图象图形学报,2006,11(12):1758-1763.

TONG Yu-bing,ZHANG Qi-shan,QI Yun-ping.Image quality assessing by combining PSNR with SSIM[J].Journal of Image and Graphics,2006,11(12):1758-1763.(in Chinese)

A Block Compressed Sensing Method Based on Multi-element Detector Array

ZHANG Zhi-quan1,DING Sheng1,2,JIN Wei-qi3
(1.Department of Control Engineering,Academy of Armored Force Engineering,Beijing 100072,China;
2.No.73021 Unit of PLA,Hangzhou 310023,Zhejiang,China;
3.Ministry of Education Key Laboratory of Photo Electronic Imaging Technology and System, Beijing Institute of Technology,Beijing 100081,China)

A block compressed sensing method is proposed considering that the calculation time of image reconstruction increases rapidly with the image size when compressive sensing(CS)theory is applied in single-pixel imaging.In the method,a digital micro-mirror device(DMD)and a multi-element detector array are used for encoding and measuring,and a total variation minimization method is used for image reconstruction,where the peak signal-to-noise ratio(PSNR)and the structural similarity(SSIM)of recovered images are improved by using gray stretch technique.Simulation results show that the method has the characteristics of shorter calculation time and higher recovered image quality.For 16 image blocks, the calculation time can be shorten by 40%at least.The PSNR and mean SSIM values of recovered images can be improved by 70%and 11%,respectively,through gray stretching of image blocks.

information processing;compressive sensing;sparse representation and reconstruction; multi-element detector array;total variation minimization with quadratic constraints;total variation mini-mization with equality constraints

TN214

:A

1000-1093(2014)05-0654-08

10.3969/j.issn.1000-1093.2014.05.012

2013-08-21

张智诠(1959—),男,教授,博士生导师。E-mail:zhangzhq123@sina.com