基于Rife法的线性调频连续波雷达测距算法及实现
詹启东,涂亚庆
(后勤工程学院后勤信息工程系,重庆 401311)
基于Rife法的线性调频连续波雷达测距算法及实现
詹启东,涂亚庆
(后勤工程学院后勤信息工程系,重庆 401311)
介绍了基于Rife法的线性调频连续波(LFMCW)雷达测距算法的原理,给出该算法的实现步骤,并从理论上分析了算法的测距性能。结合可编程门阵列(FPGA)EP3C55F484C8N芯片,进行该算法的编程实现,并将算法嵌入高精度LFMCW雷达中。利用LFMCW雷达进行现场测距实验,实验结果验证了该算法的有效性。
雷达工程;雷达测距;Rife法;线性调频连续波;可编程门阵列
0 引言
高精度线性调频连续波(LFMCW)雷达测距一直是近年的研究热点,已广泛应用于军工领域[1-4]。根据雷达测距原理,LFMCW雷达的发射信号与反射信号混频输出的差拍信号存在规则区和非规则区,通过采用高精度的频率估计方法估计规则区差拍信号的频率,对提高雷达测距精度起着重要作用[5-6]。
目前主要有4类高精度频率估计方法:比值法[7]、能量重心法[8]、快速傅里叶变换(FFT)+傅里叶变换(FT)谱连续细化分析FT法[9]和相位差法[10]。实际工程应用中的LFMCW雷达主要采用可编程门阵列(FPGA)进行差拍信号的处理,由于FPGA片内资源有限和雷达实时性的要求,使得差拍信号的处理不能过于复杂。很多算法因较为复杂,如其他算法具有求相位、求离散时间傅里叶变换(DTFT)、复数乘加法等环节都不易进行FPGA实现,不适用于雷达差拍信号的处理;而Rife法[11]作为比值法的一种,具有原理简单、易于工程实现等优点,非常适合于差拍信号的处理。
基于提高LFMCW雷达测距精度的需要,本文给出一种基于Rife法的LFMCW雷达测距算法,探索将该算法实现于LFMCW雷达中,并通过雷达的现场测距实验验证本文算法的有效性。
1 测距算法
1.1 算法原理
差拍信号作为LFMCW雷达提取距离信息的信号源,为避免其非规则区对雷达测距精度的影响,本文仅针对规则区差拍信号进行分析处理。
理想情况下,规则区差拍信号为单一频率正弦形式,故设在0~T(T为调频周期)时间内,噪声环境中规则区差拍信号经采样后为
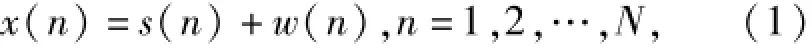
式中:s(n)=acos(2πf0n/fs+θ0),其中a、f0、θ0分别为规则区的差拍信号的幅度、频率和初相;fs为采样频率;w(n)为噪声序列;N为样本数。
x(n)的N点FFT为X(k)=S(k)+W(k)(k= 0,1,…,N-1),鉴于实序列FFT的对称性,故仅对X(k)的前N/2点进行幅值搜索。记X(k)幅度最大值为A1,对应的谱线位置为k1,幅度次大值为A2,其位置为k2,且k2=k1±1.则采用Rife法得到的规则区差拍信号频率估计值[11]为

式中:当k2=k1+1时,r= 1;当k2=k1-1时,r=-1.
对于LFMCW雷达,以锯齿波调频为例,雷达的距离测量值[6]

式中:K=cT/2B,c为电磁波传播速度,B为调频带宽。
1.2 算法步骤
根据算法原理,可得算法实现步骤如下:
1)获取规则区差拍信号x(n).实现方法为:采用同步技术,记录压控振荡器(VCO)调频信号的起始调频时刻;采用时间窗技术,仅截取规则区差拍信号x(n).
2)对信号x(n)做N点FFT,找出X(k)前N/2点中的最大幅值A1和次大幅值A2,及其各自的位置k1和k2.
3)利用(2)式估计信号x(n)的频率^f0.
4)利用(3)式计算距离R.
1.3 算法性能
为便于分析本文算法的测距性能,给出FFT距离谱的概念及其获取方式如下:假设FFT幅度谱的横轴变量为频率fi=iΔf(i=0,1,…,N-1),纵轴变量为傅里叶系数的绝对值|X(i)|,将其横轴变量fi转换为距离Ri=Kfi,纵轴变量保持不变,所得新FFT谱本文将其称之为FFT距离谱,如图1所示。

图1 FFT距离谱Fig.1 FFT range spectrum
图1中ΔR=KΔf为相邻谱线之间的间隔,即距离分辨力,Δf为频率分辨率;δR为真实距离与距离谱中最大谱线所对应距离的差值与ΔR的比值。
在理想无噪声环境下,X(k)幅度最大值A1= |S1|,次大值A2=|S2|,第3大值A3=|S3|,k3= k2±2.不加窗(即加矩形窗)FFT距离谱中最大谱线和次大谱线始终位于sinc函数的主瓣内,第3大谱线则位于最大谱线另一侧的第1旁瓣内,可证明始终有A2>A3[12].文献[12]表明在无噪声环境下Rife法可获得准确的频率估计值,故根据(3)式本文算法同环境下可准确获得距离值。
但在实际工程应用中,信号不可避免存在噪声的干扰,A1、A2和A3确切应表示为

式中:W1、W2、W3分别为迭加在S(k)幅度最大值、次大值、第3大值处的噪声。
噪声环境下算法的性能分析可分为2种情况:
1)当δR接近0时,即真实距离位于量化距离点附近时,|S2|与|S3|均接近0,由于存在迭加噪声W2和W3,故可能出现A2<A3的情况。此时测距误差较大,其误差主要是因噪声引起次大谱线误判而导致的插值方向错误所致。如:假设真实距离为R0= (k0-δR)ΔR,则本文算法得到的距离值可能为^R0=(k0+δR)ΔR,距离测量将出现(2δR)ΔR的误差。
2)当δR不接近0时,即真实距离不位于量化距离点附近时,|S2|较大且|S2|≫|S3|,即使存在迭加噪声W2和W3也不会出现A2<A3的情况。此时测距误差较小,其误差主要来源于噪声对|S1|和|S2|幅值估计的影响。
2 算法实现
实验室现有LFMCW雷达应用FPGA进行规则区差拍信号的处理,FPGA型号为Altera公司的CycloneⅢ系列EP3C55F484C8N.基于该FPGA芯片探索实现本文算法,并将算法嵌入LFMCW雷达中。
2.1 FPGA设计
利用QuartusⅡ软件新建一个目标器件为EP3C55F484C8N的可编辑工程文件,针对该器件进行程序设计、编译、绑定管脚和再编译等步骤,得到的设计结果如图2所示。

图2 FPGA设计的RTL图Fig.2 RTL diagram of design for FPGA
程序设计主要由1个FFT模块、2个控制模块、1个功率计算模块、2个RAM模块、2个功率谱搜索模块和1个距离计算模块组成。各模块功能如下:
1)控制模块1用于控制FFT模块仅对规则区差拍信号做FFT运算;
2)功率计算模块用于实现FFT模块输出的实部和虚部到功率的换算,并输出功率值;
3)控制模块2用于实现将功率值同时存入2个RAM模块中;
4)2个功率谱搜索模块用于实现对2个RAM模块中功率值的搜索,找出最大功率值和次大功率值,并记录其各自的位置;
5)距离计算模块用于实现对功率值进行开方,并根据(2)式和(3)式获得距离值。
设计中FFT模块通过配置FFT IP核来实现,其他模块采用VHDL语言编程实现。此外,规则区差拍信号以16位二进制表示,FFT运算点数为4 096,时钟频率取500 kHz.
2.2 FPGA资源消耗
应用QuartusⅡ软件对所建工程文件进行编译,得到FPGA资源使用情况如表1所示。

表1 FPGA资源消耗表Tab.1 Resource consumption of FPGA
可见,本文算法能够在FPGA EP3C55F484C8N芯片内进行编程实现,且占用资源较少,同时该芯片备有富余资源以供进一步改进算法。
2.3 算法嵌入
将本文算法嵌入实验室LFMCW雷达中(雷达实物见图3),实现步骤如下:
1)应用QuartusⅡ软件将2.1节的FPGA设计嵌入LFMCW雷达的可编辑工程文件中;
2)对该工程文件进行编译,获得下载文件(即SOF文件);
3)应用USB-Blaster下载器将SOF文件下载至LFMCW雷达中,即实现本文算法的嵌入。
图3 LFMCW雷达实物图Fig.3 Diagram of LFMCW radar
3 算法实验
为检验本文算法的测距性能,并与工程中广泛应用的FFT法(利用FFT距离谱中最大谱线对应的距离作为目标距离估计值)的测距性能进行对比。
利用LFMCW雷达进行现场测距实验。LFMCW雷达参数为:采用锯齿波调制,信号中心频率f0= 25 GHz,调频带宽B=1 GHz,调频周期T=10 ms,采样频率fs=500 kHz,FFT点数N=4 096.该雷达有效测距范围5~20 m,实际距离分辨力ΔR=167 mm.

如表2所示,给出了本文算法和FFT法的实验结果,表中δR=(Rn-R0)/ΔR.
如图4所示为本文算法和FFT法的误差分布。
由表2和图4可看出:
1)当Rn位于6.300~6.340 m区域,即δR位于-0.14~+0.10区域时,本文算法误差范围约20~40 mm,略大于FFT法的误差。
2)当Rn位于6.260~6.300 m或6.340~6.380 m区域,即δR位于-0.38~-0.14或+0.10~+0.34区域时,本文算法误差范围约10~20 mm,略小于FFT法的误差。
3)当Rn位于6.240~6.260 m或6.390~6.407 m区域,即δR位于-0.50~-0.38或+0.40~+0.50区域时,本文算法误差在10 mm以内,远小于FFT法的误差。

表2 实验结果明细表Tab.2 Experimental results

图4 误差分布图Fig.4 Diagram of error distribution
4)采用本文算法和FFT法进行测距,所得结果均方根误差分别为18.6 mm和44.1 mm,平均绝对误差分别为17 mm和40 mm.
与FFT法的计算量相比,本文算法在FFT法的基础上,增加了(2)式的计算。引起的计算量变化为:本文算法比FFT法增加了4次乘法和2次加法运算,增加的计算量较小,可忽略不计。因此,本文算法的计算速度与FFT法相当,且本文算法原理简单,同样易于工程实现。
4 结论
基于提高LFMCW雷达测距精度的需要,本文给出一种基于Rife法的LFMCW雷达测距算法。与工程中广泛应用的FFT法相比,本文算法可在一定程度上改善雷达的测距精度。
实验结果表明:当0.14∞|δR|∞0.5时(占整个距离谱的72%),本文算法的精度高于FFT法的精度;当|δR|<0.14时(占整个距离谱的28%),真实距离位于有限量化距离点附近,本文算法的精度略低于FFT法的精度。
因此,通过确定一个算子以判定当真实距离位于量化距离点附近时,采用FFT法进行测距,其他区域均采用本文算法,可进一步改善雷达的测距精度。
References)
[1] Liu Y,Deng Y K,Wang R,et al.Bistatic FMCW SAR signal model and imaging approach[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(3):2017-2028.
[2] 蒋留兵,林和昀,柴林峰,等.多目标LFMCW车载前向防撞雷达的实现[J].现代雷达,2012,34(6):26-29.
JIANG Liu-bing,LIN He-yun,CHAI Lin-feng,et al.Implementation of multiple target LFMCW vehicle forward anticollision radar[J]. Modern Radar,2012,34(6):26-29.(in Chinese)
[3] Xu Q,Wang Y L,Ren K C,et al.Study on rapid linearity detection of LFMCW radar[C]∥2011 International Conference on E-lectric Information and Control Engineering.Wuhan:IEEE,2011: 1738-1741.
[4] 侯志,缪晨,吴文,等.一种对称三角线性调频连续波雷达的校正算法[J].兵工学报,2010,31(12):1546-1550.
HOU Zhi,MIAO Chen,WU Wen,et al.A kind of calibration algorithm of symmetrical triangular linear frequency modulated continuous wave radar[J].Acta Armamentarii,2010,31(12):1546-1550.(in Chinese)
[5] 丁鹭飞,耿富录,陈建春.雷达原理[M].第4版.北京:电子工业出版社,2009:273-280.
DING Lu-fei,GENG Fu-lu,CHEN Jian-chun.Radar principle [M].4th ed.Beijing:Publishing House of Electronics Industry, 2009:273-280.(in Chinese)
[6] 崔占忠.调频测距信号分析[J].探测与控制学报,2006, 28(5):1-3.
CUI Zhan-zhong.Analysis of frequency modulation ranging[J]. Journal of Detection&Control,2006,28(5):1-3.(in Chinese)
[7] 柏林,董鹏飞,刘小峰,等.比值法的频率估计精度分析[J].重庆大学学报,2010,33(10):7-13,31.
BO Lin,DONG Peng-fei,LIU Xiao-feng,et al.Accuracy analysis for frequency estimation of amplitude ratio method[J].Journal of Chongqing University,2010,33(10):7-13,31.(in Chinese)
[8] 丁康,江利旗.离散频谱的能量重心校正法[J].振动工程学报,2001,14(3):354-358.
DING Kang,JIANG Li-qi.Energy centrobaric correction method for discrete spectrum[J].Journal of Vibration Engineering,2001, 14(3):354-358.(in Chinese)
[9] 刘进明,应怀樵.FFT谱连续细化分析的傅里叶变换法[J].振动工程学报,1995,8(2):162-166.
LIU Jin-ming,YING Huai-qiao.Zoom FFT spectrum by Fourier transform[J].Journal of Vibration Engineering,1995,8(2): 162-166.(in Chinese)
[10] 丁康,钟舜聪.通用的离散频谱相位差校正方法[J].电子学报,2003,31(1):142-145.
DING Kang,ZHONG Shun-cong.Auniversal phase difference correcting methods on discrete spectrum[J].Acta Electronica Sinica,2003,31(1):142-145.(in Chinese)
[11] Rife D C,Vincent G A.Use of the discrete Fourier transform in the measurement of frequencies and levels of tones[J].Bell System Technical Journal,1970,49(2):197-228.
[12] 齐国清,贾欣乐.插值FFT估计正弦信号频率的精度分析[J].电子学报,2004,32(4):625-629.
QI Guo-qing,JIA Xin-le.Accuracy analysis of frequency estimation of sinusoid based on interpolated FFT[J].Acta Electronica Sinica,2004,32(4):625-629.(in Chinese)
Analysis and Implementation of Rife-based Ranging Algorithm for Linear Frequency Modulated Continuous Wave Radar
ZHAN Qi-dong,TU Ya-qing
(Department of Logistical Information and Engineering,Logistical Engineering University,Chongqing 401311,China)
A rife-based ranging algorithm for linear frequency modulated continuous wave(LFMCW)radar is proposed.The principle and implementation step of algorithm are presented,and the ranging performance of algorithm is discussed.The implementation method of algorithm is explored in conjunction with the chip of field programmable gate array(FPGA)EP3C55F484C8N,and the algorithm is embed in LFMCW radar.Finally,the experimental results derived from the field ranging experiment of LFMCW radar prove the validity of the algorithm.
radar engineering;radar ranging;Rife method;linear frequency modulated continuous wave;field programmable gate array
TN959.1
:A
1000-1093(2014)05-0748-05
10.3969/j.issn.1000-1093.2014.05.025
2013-07-15
国家自然科学基金项目(61271449、61302175);重庆市自然科学基金项目(CSTC2011BA2015、CSTC2012jjA40006)
詹启东(1988—),男,硕士研究生。E-mail:zhanqd@syvip.com;
涂亚庆(1963—),男,教授,博士生导师。E-mail:yqtcq@sina.com

