人-枪系统中不同自动方式对枪械后坐作用影响研究

王长庚,徐万和,徐诚

(南京理工大学机械工程学院,江苏南京 210094）

人-枪系统中不同自动方式对枪械后坐作用影响研究

王长庚,徐万和,徐诚

(南京理工大学机械工程学院,江苏南京 210094）

为了研究枪械在人-枪系统中后坐作用的特性和影响因素,基于不同自动方式下枪械的内弹道特性、后坐机理以及枪机运动,结合刚体动力学和碰撞动力学,分别建立了在立姿射击时,考虑人-枪作用的导气式和自由枪机式两种枪械后坐作用的动力学模型,并对枪械在人-枪作用过程中的后坐作用力、后坐速度、肩部水平位移等特征物理量进行数值分析和实验分析。研究结果表明:两种不同自动方式的枪械后坐作用力、射手的后坐速度和位移随后坐时间的变化规律、最大值出现的次数和时间并不相同。

兵器科学与技术;枪械;后坐作用;动力学;数值分析

0 引言

枪械的后坐作用是枪械考核的一个重要技术指标。而在人-枪系统中,枪械的自动方式是影响枪械后坐作用的一个因素。现有的研究工作在分析自动方式对枪械后坐作用影响时,并没有考虑发射过程中自动机运动对人-枪系统和枪械后坐作用的影响,针对后坐作用过程进行细致的分段建立模型。

本文针对枪械在人-枪系统射击过程中,根据自动机不同阶段的运动状态,基于相同的约束条件,分别建立了立姿射击时,导气式和自由枪机式这两种自动方式的动力学模型,并对其进行数值和实验分析,研究其对枪械后坐作用的影响。

1 枪械后坐作用动力学模型

为了便于分析计算,将立姿射击时,枪械后坐作用模型简化,如图1所示。

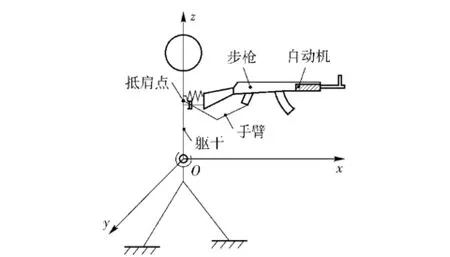
图1 枪械后坐作用力学模型示意图Fig.1 Mechanical model of gun recoil effect

在立姿射击时,射手手臂将枪械抵于射手肩部,进行射击。根据以往实验观察和数据[1-3],对模型做出以下假设:

1)将射手躯干等效为一绕z轴水平旋转和绕y轴俯仰转动的刚体质量块。

2)枪托和抵肩点之间用一个弹性约束和一个阻尼器来描述;枪托和抵肩点之间无相对水平旋转。

3)假设射手紧握枪械,枪械和射手手臂之间无相对运动,并将射手手臂质量转换成枪械的等效质量。

4)假设以射手臀腰为坐标原点O,射手躯干绕臀腰转动、手臂绕躯干转动,且其之间的阻尼系数为常数,并用一个阻尼器来描述。

5)将射手对枪械的预紧作用假设为分别作用在腰部水平转动、俯仰转动以及枪械相对肩部的俯仰转动上的预紧力偶和手臂对枪械水平方向上的预紧力;预紧力偶具有摩擦力的一些特性,在枪械后坐运动过程中仅起到阻力的作用。

根据以上假设,结合多刚体动力学,建立枪械立姿射击下,后坐作用的动力学模型,如图2所示,点A、B、E分别为枪械(不含自动机)、躯干以及自动机的质心。点D为抵肩支撑点;K为肩部约束刚度系数;C为肩部水平约束的阻尼系数;C1为躯干俯仰转动的阻尼系数;C2为躯干水平旋转的阻尼系数;C3为枪械相对肩部俯仰转动的阻尼系数;M1为躯干俯仰转动的预紧力偶;M2为躯干水平自转的预紧力偶; M3为枪械相对肩部的俯仰转动的预紧力偶。

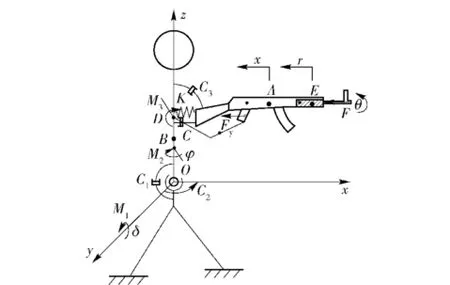
图2 枪械后坐作用动力学模型Fig.2 Dynamic model of gun recoil effect

根据多刚体动力学理论,模型为3刚体5自由度,假设,x、r、θ、δ以及φ为系统的5个广义坐标。其中:x为步枪的水平后坐位移;r为自动机的相对机匣的后坐位移;θ为枪械绕抵肩点的俯仰转动角度;δ为躯干绕腰部的俯仰转动角度;φ为躯干绕腰部的水平转动角度。同时,考虑导气式枪械的开锁机构,仅就导气式枪械后坐作用模型添加一个广义坐标r1,r1为枪机框开锁前的相对机匣的后坐位移。

2 导气式枪械后坐作用分析

导气式是利用导出的膛内火药燃气使枪机后坐的自动方式[4]。弹丸击发后,在弹丸未经过导气孔时,枪机还未开锁,此时枪机和机匣在膛内压力的作用下一起后坐,故可将该阶段称之为开锁前期;当弹丸经过导气孔,枪机框开始在导气室内的燃气压力下,后坐运动完成开锁动作,此阶段,自动机开始解锁,故称之为开锁阶段;开锁后,自动机开始惯性后坐,直至自动机后坐到位,撞击机匣,故可称之为自动机惯性后坐阶段;最后自动机在复进簧作用下复进,直到复进到位,撞击机匣,进行下次射击动作。

根据上述分析,可将导气式枪械的划分为:开锁前期、开锁阶段、自动机惯性后坐阶段以及自动机复进阶段。

2.1 开锁前期

开锁前期这一阶段,从弹丸击发开始,到弹丸经过导气孔结束。该阶段,由于枪机还未开锁,可以将枪机、枪机框和机匣看为一个整体,受膛内火药燃气的压力,射手受到枪械后坐产生的后坐作用力(矩)和预紧力(偶)。该阶段,系统的动力学方程为

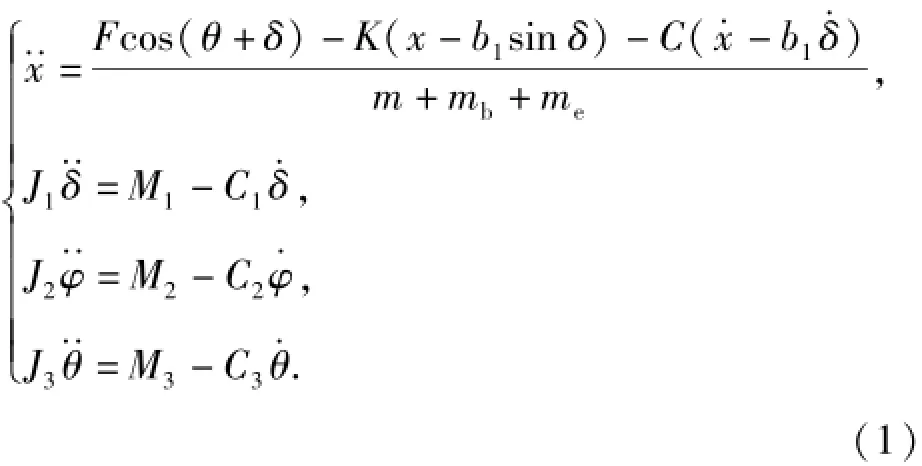
式中:me为枪械的等效质量(不包含自动机);m为枪机框质量;mb为枪机质量;F为膛内火药燃气压力,F=S·p,S为线膛横截面积,p为膛内平均压力[5];J1为躯干绕腰部O点的俯仰转动惯量;J2为躯干绕腰部O点的水平转动惯量;J3为步枪绕支撑点D的转动惯量;M1为躯干受到的俯仰转动合力矩; M2为躯干受到的水平转动合力矩;M3为枪械受到的相对肩部俯仰转动的合力矩;b1为抵肩点到腰部的直线距离OD.

2.2 开锁阶段

开锁阶段,是从枪机框开始自由行程到枪机完全开锁,枪机和枪机框一起开始惯性后坐。该阶段,枪机框在导气室内燃气压力和复进簧的作用下后坐,在走完开锁前自由行程后,撞击枪机,完成开锁,并和枪机一起开始惯性后坐,同时,在枪机还未开始相对机匣后坐时,枪机依然和机匣一起,在膛内火药燃气的作用下继续后坐,直至枪机框撞击枪机,使得枪机和机匣分离。

由于枪机框撞击枪机开锁时,弹头早已飞出膛口,膛内压力急剧下降,故简化计算,可忽略开锁时的抽壳阻力和此时的膛内火药燃气压力。在此阶段,机匣受到气室内火药燃气对气室前端面的作用力Fs,其数值近似等于枪机框所受到的气室内燃气压力,整个系统的动力学方程为

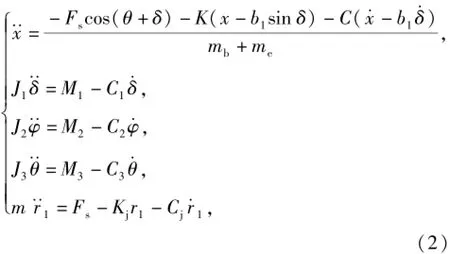
式中:Kj为复进簧刚度;Cj为复进簧阻尼系数;Fs为导气室内火药燃气压力,Fs=Ss·ps,Ss为导气室横截面积,ps为气室内平均压力[5],pd为弹头经导气孔瞬

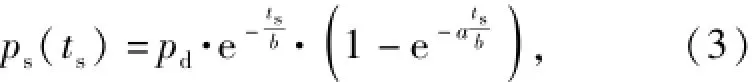
式中:ts为开锁阶段的总时间,从弹丸经过导气孔开始,到枪机框走完开锁前自由行程结束;a为结构系数;b为时间系数。

2.3 自动机惯性后坐阶段

自动机惯性后坐阶段,是从枪机和枪机框开始惯性后坐到其后坐到位撞击机匣。该阶段,机匣和自动机惯性后坐,受到复进簧力,而射手也惯性后坐,受到预紧力偶的阻力,此时,系统的动力学方程为间的膛内平均压力。采用布拉文的经验公式[5]

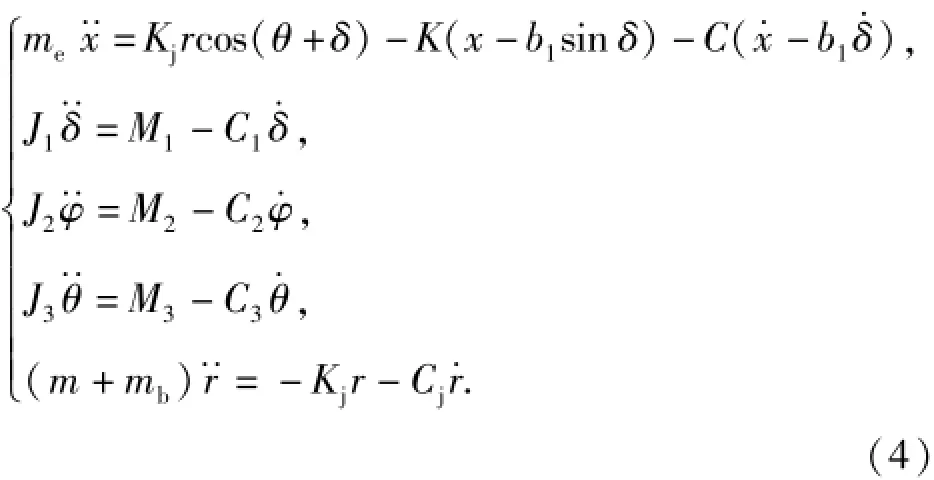
该阶段方程未知变量的初始值应该为上一阶段的终止值,但由于枪机框撞击枪机开锁,导致枪机框和枪机的速度发生瞬间变化,故该阶段自动机的初始速度应该为碰撞后的瞬时值,同时,该碰撞为碰撞结合,其碰撞恢复系数b0可取为0,碰撞后的速度由(10)式可得。

2.4 自动机复进阶段

自动机复进阶段,是从枪机和枪机框开始复进到其复进到位撞击机匣前端。该阶段,系统只受到射手的预紧力(偶)和复进簧力,此时,系统的动力学方程为

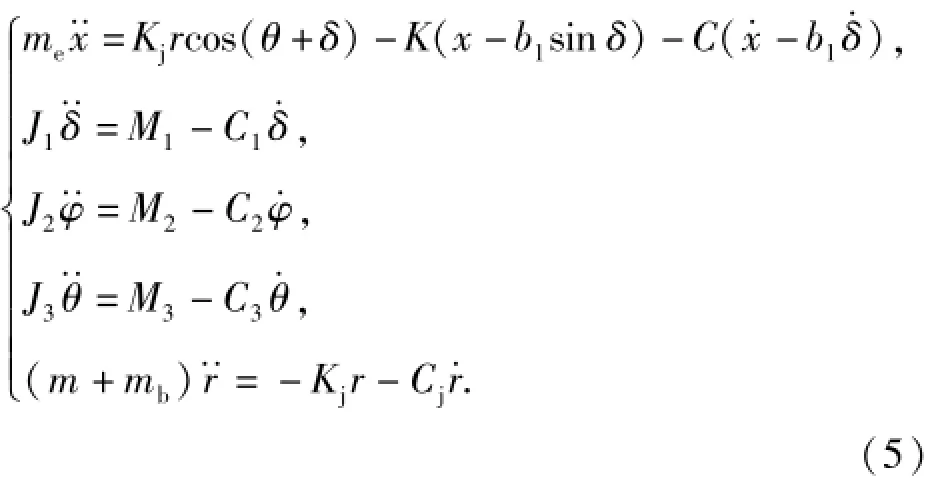
该阶段方程未知变量的初始值应为自动机撞击机匣后的瞬时值,而该碰撞为撞击分离,根据(10)式和碰撞原理,可得碰撞后各构件的瞬时速度。而该阶段,复进到位碰撞后,各构件的瞬时速度将作为下一循环的初始值。

3 自由枪机式枪械后坐作用分析

自由枪机式是利用枪机后坐运动能量进行工作的自动方式[4]。自由枪机式枪械,当枪弹击发后,枪机在膛内火药燃气的作用下就开始后坐,同时,完成抽壳动作,直到枪机后坐到位,撞击机匣;然后在复进簧的回复力的作用下,枪机开始复进,直至复进到位,撞击机匣,进入下一次射击动作。

根据自由枪机式枪械的后坐过程,整个过程可分为:抽壳阶段、枪机自由后坐阶段以及枪机复进阶段3个阶段。

3.1 抽壳阶段

该阶段,枪弹击发时,由于枪机是靠惯性闭锁,没有相应机构限制其后坐运动,故枪机在膛内火药燃气和膛壳间摩擦力的作用下,开始后坐运动。但抽壳过程中,膛壳间的摩擦阻力较为复杂,为了简化计算,引入了枪机质量虚拟系数。

此阶段,整个系统的动力学方程为

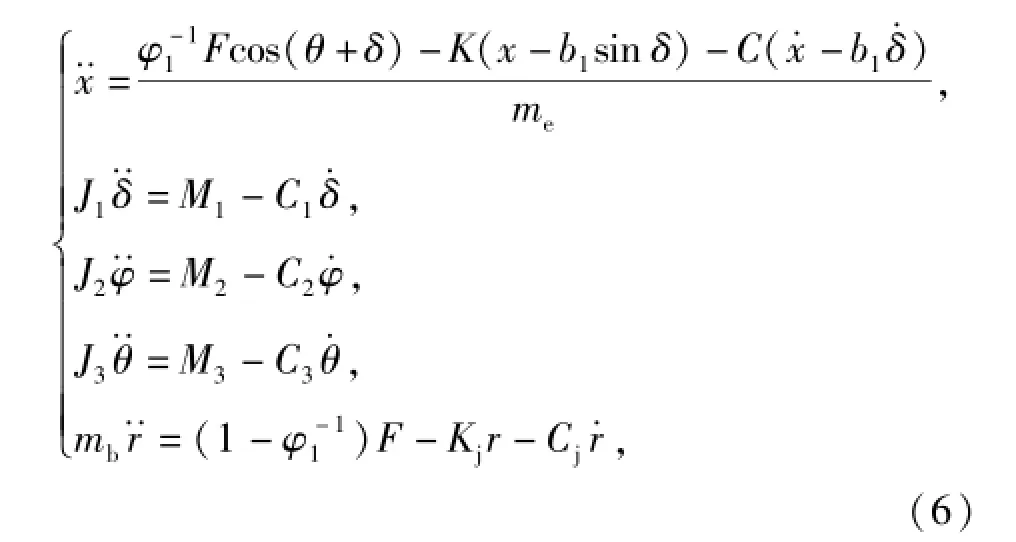
式中:φ1为枪机质量虚拟系数[5],可取为1.3.

式中:v0为碰撞后枪机和机匣的前冲速度;v1为碰撞前枪机的前冲速度,根据击发前,复进簧的压缩量和枪机质量近似计算获得。

自由枪机常采用前冲式击发,使得枪械在枪弹击发前已经具有一定的速度,由于从枪弹击发到枪机撞击机匣前端面的时间很短,枪机和机匣所受外力相对碰撞力较小,为便于分析,可以认为系统所受合外力为0.根据碰撞理论,可得

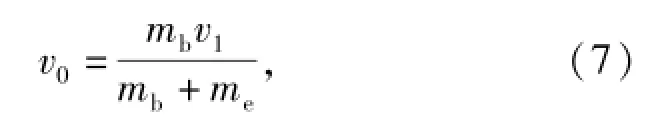
3.2 枪机惯性后坐阶段

枪机惯性后坐阶段,从内弹道结束到枪机后坐到位,撞击机匣。该阶段的初始时期,虽然弹壳还未完全从膛内抽出,但膛内压力已经急剧下降,弹壳所受的合外力也急剧下降,为便于分析,可认为此时枪机仅在复进簧的作用下惯性后坐,系统的动力学方程为

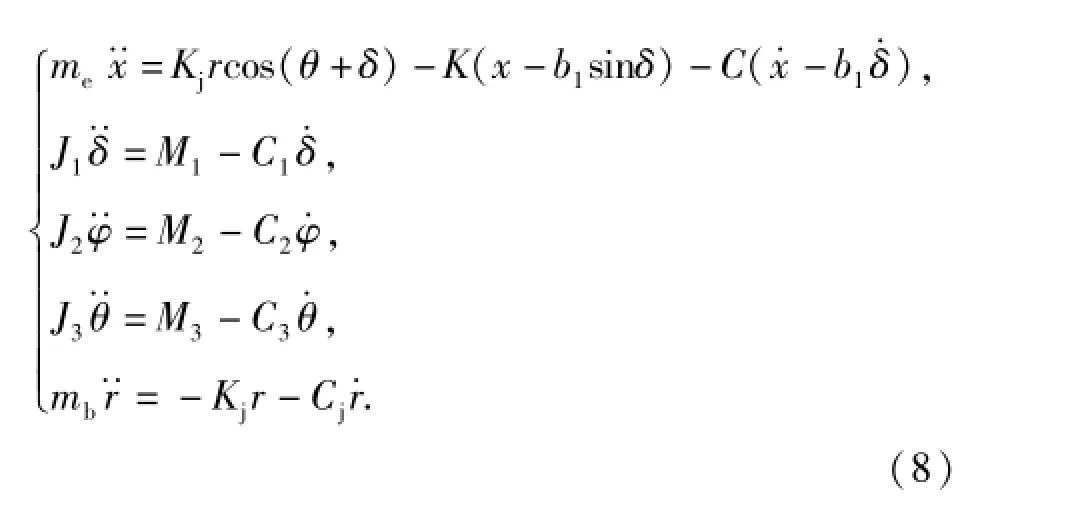
3.3 枪机复进阶段

枪机复进阶段,从枪机开始复进到枪机复进到位,撞击机匣前端。该阶段,枪机仅在复进簧的作用下自由后坐。此时系统的动力学方程为

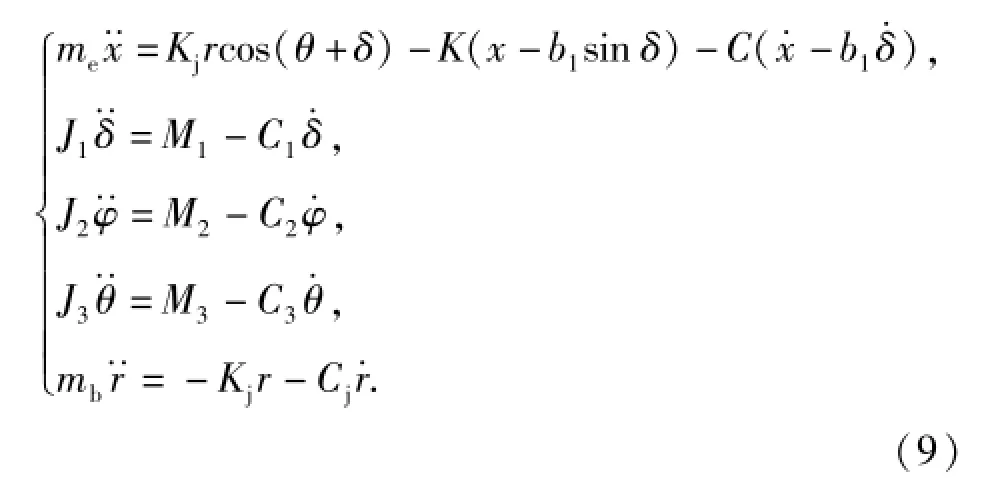
该阶段方程未知变量的初始值应为自动机撞击机匣后的瞬时值,而该碰撞为撞击分离,根据(10)式和碰撞原理,可得碰撞后各构件的瞬时速度。而该阶段,复进到位碰撞后,各构件的瞬时速度将作为下一循环的初始值。

4 数值计算与分析

枪械后坐作用的动力学方程为微分方程组。本文采用4阶龙格-库塔的数值计算方法,借用Matlab软件进行数值分析。同时,根据模型的特性,在动力学方程的求解过程中,考虑了碰撞计算和约束的判定。

4.1 碰撞计算

在枪械后坐运动中,会出现多次碰撞,这些碰撞不仅作用时间极短,而且往往引起构件速度的急剧变化。为了便于分析计算,本文采用将每次碰撞作为各个阶段的初始点或者中止点。考虑到碰撞时,系统所受合外力远小于碰撞力,可认为系统合外力为0,根据碰撞理论,可得碰撞件碰撞后的速度

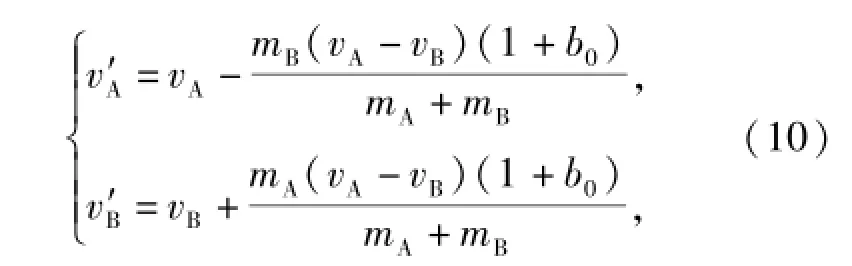
式中:mA、mB分别为碰撞件A、B的质量;vA、vB分别为碰撞件A、B撞击前的速度;b0为碰撞恢复系数。

4.2 约束判定

在立姿射击中,由于射手对枪械的预紧力偶具有与摩擦力相似的力学特性,所以需要在每一个阶段动力学方程的求解过程中,对支撑体所受的合外力矩进行判定。以躯干绕腰部的俯仰力矩为例,其判定条件如下:

1)当躯干俯仰速度为0,同时,躯干受到的动力矩M1d小于预紧力偶My时,其合外力矩M1为0.

2)当不满足条件1时,由于整个系统受力平衡,躯干所受合外力矩M1为

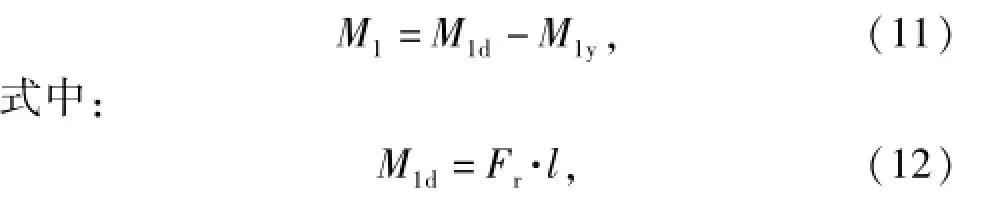
式中:l为枪械后坐作用力到腰部回转轴的力臂;Fr为枪械后坐作用力,其值为

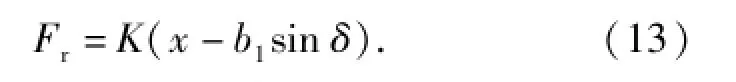
同理,躯干水平转动的合力矩M2以及枪械相对肩部俯仰转动的合力矩M3,都可依据该方法进行判定。

4.3 计算参数诸元

为了直观地表现不同自动方式对枪械后坐作用的影响,本文以使用同一种枪弹的79式冲锋枪和85式冲锋枪作对比。

由于射手射击时的相关结构参数的非确定性,同时,为了便于分析,本文根据相关文献资料[6],确定了立姿射击动力学方程中的主要相关诸元以及两种枪械的主要相关参数,如表1、表2所示。

表1 约束主要相关诸元Tab.1 Main data of constraint

表2 枪械主要相关参数Tab.2 Main data of gun

4.4 仿真结果与分析

在表1、表2所示诸元下,85式冲锋枪和79式冲锋枪的后坐作用力Fr随时间t的变化曲线如图3所示。

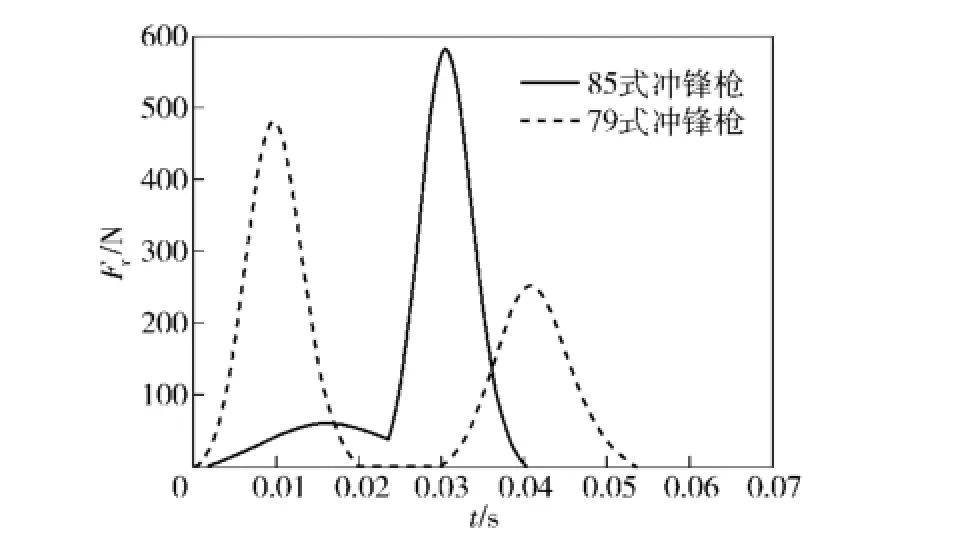
图3 后坐作用力对比曲线Fig.3 Curves of recoil forces

导气式枪械由于其自动方式的原因,在弹头未经过导气孔时,枪机还未开锁,膛内火药燃气压力通过枪机作用于整个枪械系统,当出现最大膛压后,产生后坐作用力峰值,但由于射手躯干的运动,导致这一峰值的最大数值降低以及作用时间增加;随着自动机后坐到位时,枪机及枪机框撞击机匣时的碰撞力,作用在整个系统上,产生后坐作用力峰值。

自由枪机式枪械由于自动方式的原因,在枪弹击发后,机匣受到的主动力仅为膛壳间的摩擦力,这一主动力相对膛内火药气体压力较小,故其后坐作用力幅值也较小;抽壳动作完成后,枪机自由后坐到位后,枪机撞击机匣,出现了较大的后坐作用力峰值。

图4所示为两种自动方式下,枪械水平速度·x的对比曲线,由图4可知:两种枪械在后坐过程中的速度都发生了两次突变,其峰值出现的时间相比枪械后坐作用力峰值出现的较早,说明枪肩的约束具有明显的缓冲作用。

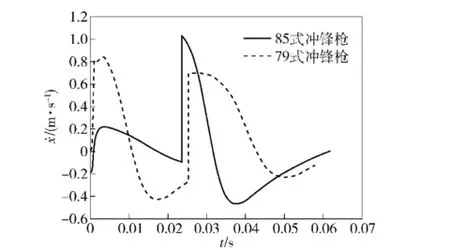
图4 枪械水平速度对比曲线Fig.4 Speed curves of guns

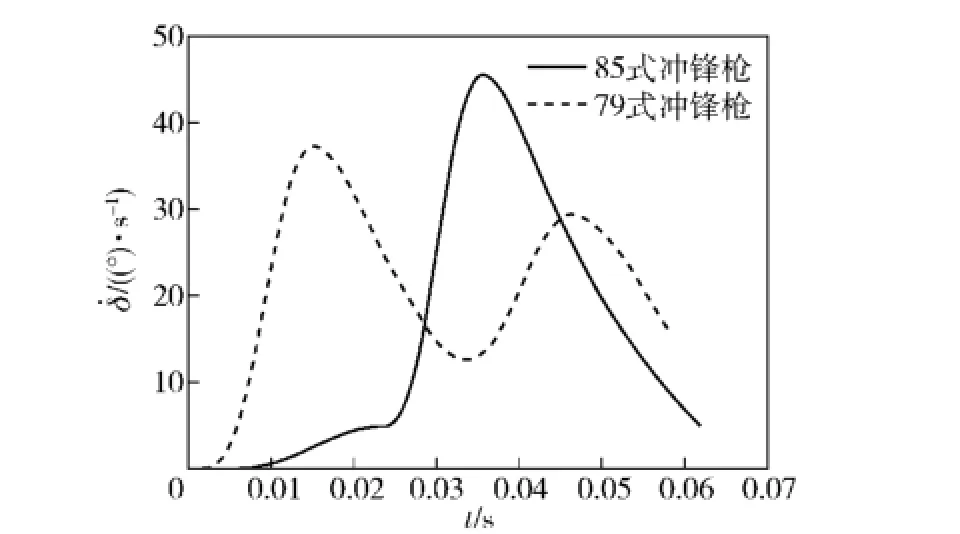
图5 躯干俯仰角速度对比曲线Fig.5 Curves of pitching angular velocity of body

图6所示为射手肩部的水平位移s对比曲线,由图6可知,虽然两种不同自动方式的枪械,其射击时,射手肩部水平位移的变化趋势都是逐渐增大的,但其增大的规律并不一样。导气式枪械射击时,射手肩部开始水平移动后,其数值先急剧增大,而后其增大速率有所放缓,然后再增大;而自由枪机式枪械,其数值先增大,而后其增大速率逐渐放缓。

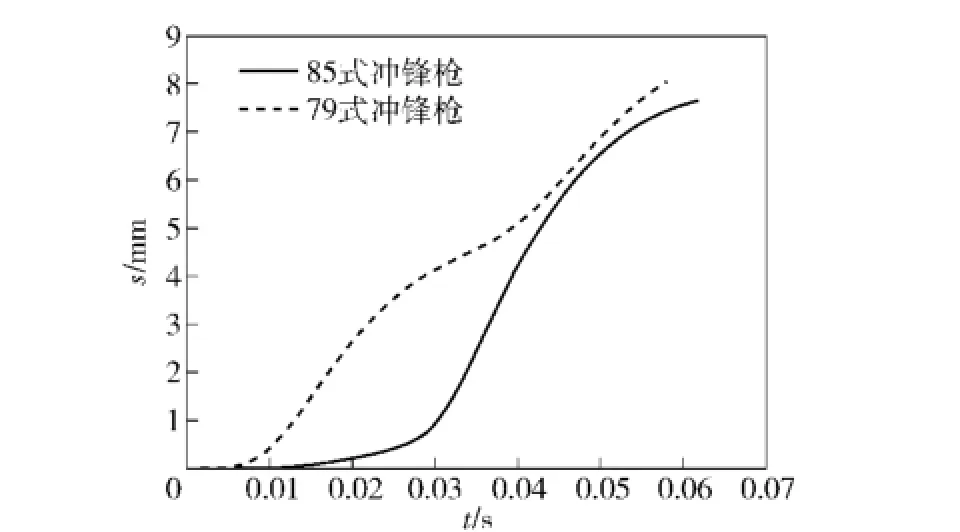
图6 肩部水平位移对比曲线Fig.6 Curves of shoulder horizontal displacement

5 实验结果与分析

5.1 实验原理

实验以79式冲锋枪和85式冲锋枪为例,采用射手射击的方式进行测量,如图7所示。射击时,枪托底部连接压电式传感器,传感器另一端抵于射手肩部上。击发后,整个系统开始后坐,传感器传出相应的电荷信号,通过电荷放大器,将信号转换成电压信号,显示于示波器中,并记录下来,同时,利用高速摄影记录射击时,射手肩部的水平位移。

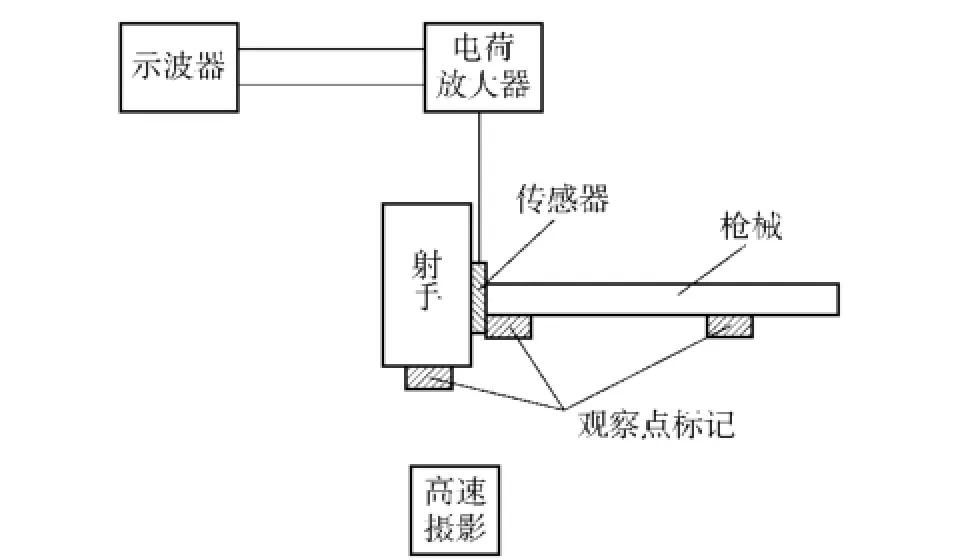
图7 射击实验原理图Fig.7 Illustrative diagram of firing experiment

5.2 实验结果分析

图8和图9所示,分别为79式冲锋枪后坐作用力实验曲线和85式冲锋枪后坐作用力实验曲线。

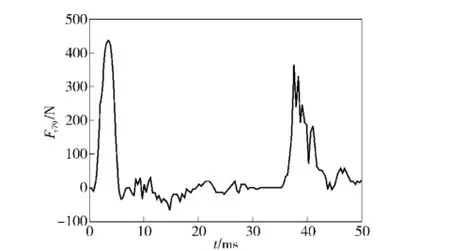
图8 79式冲锋枪后坐作用力实验曲线Fig.8 Experimental curve of recoil force of 79 type submachine gun

由图8和图9可以看出:在该实验条件下,79式冲锋枪的后坐力曲线出现两次峰值,其最大后坐作用力为435.8 N.85式冲锋枪的最大后坐作用力为487.6 N.

图10所示为两种枪械肩部水平位移s的实验曲线。由图10可知,85式冲锋枪在该条件下射击时,射手肩部最大水平位移为6.55 mm;79式冲锋枪在该条件下射击时,射手肩部最大水平位移为7.58 mm.

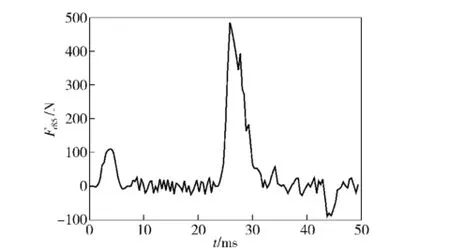
图9 85式冲锋枪后坐作用力实验曲线Fig.9 Experimental curve of recoil force of 85 type submachine gun

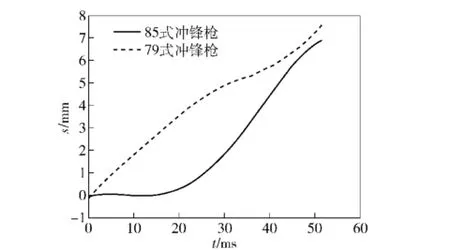
图10 两种枪械肩部水平位移实验曲线Fig.10 Experimental curves of shoulder horizontal displacements of 79 and 85 type submachine guns

由于为了便于分析,模型建立中进行了简化,故实验数据与仿真结果相比有一定的差异,但枪械后坐作用力的作用规律基本一致。

6 结论

1)本文建立了立姿射击时,考虑人-枪相互作用的两种不同自动方式枪械后坐作用理论模型,为枪械后坐作用精细化的预测提供了基本方法。

2)在使用同一种枪弹以及约束条件相同的情况下:导气式枪械,第一后坐冲量引起的后坐力明显大于自动机第二后坐冲量引起的后坐力;自由枪机式枪械,第一后坐冲量引起的后坐力远远小于枪机后坐到位冲击引起的后坐力。

3)基于不同自动方式,后坐力的作用规律并不相同,人体躯干的运动状态也不相同,导气式自动方式下,射手躯干的俯仰角速度有两次明显的峰值;而自由枪机自动方式下,射手躯干的俯仰角速度只有一次明显的峰值。

4)两种自动方式下,不同后坐作用力规律和射手躯干的运动规律对连发射击时需要的稳定操控方式以及枪械后坐作用的测评提供了一定的理论参考。

References)

[1] Schiehlen W,Guse N,Seifried R.Multibody dynamics in computational mechanics and engineering applications[J].Computer Methods in Applied Mechanics and Engineering,2006,195(41/ 42/43):5509-5522.

[2] Slavic J,Boltezar M.Simulating multibody dynamics with rough contact surfaces and run-in wear[J].Nonlinear Dynamics,2006, 45(3/4):353-3115.

[3] 姚养无,王刚,师翼,等.弹簧液压式延迟后坐枪机的动力学仿真[J].兵工学报,2008,29(5):518-520.

YAO Yang-wu,WANG Gang,SHI Yi,et al.Dynamic simulation of spring-hydraulic delayed bolt[J].Acta Armamentarii,2008, 29(5):518-520.(in Chinese)

[4] 欧学炳,殷仁龙,王学颜.自动武器结构设计[M].北京:兵器工业出版社,1992:174-189.

OU Xue-bing,YIN Ren-long,WANG Xue-yan.Automatic weapons structure design[M].Beijing:Publishing House of Ordnance Industry,1992:174-189.(in Chinese)

[5] 甘高才.自动武器动力学[M].北京:兵器工业出版社,1990: 30-75.

GAN Gao-cai.Automatic weapons dynamics[M].Beijing:Publishing House of Ordnance Industry,1990:30-75.(in Chinese)

[6] 包建东,王昌明,何云峰,等.人-枪模型的建立及仿真分析[J].兵工学报,2009,30(5):513-517.

BAO Jian-dong,WANG Chang-ming,HE Yun-feng,et al.Foundation of man-gun model and simulation analysis[J].Acta Armamentarii,2009,30(5):513-517.(in Chinese)

Research on the Influence of Different Automatic Action of Gun on Its Recoil Effect in Man-gun System

WANG Chang-geng,XU Wan-he,XU Cheng
(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)

In order to study the characteristics and influence factors of recoil effect of gun in the man-gun system,two dynamic models for the recoil effects of gas-operated and simple blowback bolt type guns for firing at the standing position are established in consideration of man-gun interaction.The models are based on gun interior ballistic properties,recoil mechanism and bolt movement in different automatic ways,rigid-body dynamics and collision dynamics.The gun recoil force,recoil velocity and shoulder horizontal displacement in man-gun system are numerically and experimentally analyzed.The research results show that the rules of the changes of gun recoil force and the shooter'recoil velocity and displacement withe recoiling time,and the number of occurrences and time of the maximum are not same for two different kinds of automatic gun.

ordnance science and technology;firearms;recoil effect;dynamics;numerical analysis

TJ156

:A

1000-1093(2014)05-0741-07

10.3969/j.issn.1000-1093.2014.05.024

2013-08-10

王长庚(1985—),男,博士研究生。E-mail:1380516@163.com;

徐万和(1954—),男,教授,硕士生导师。E-mail:xuwanhe@mail.njust.edu.cn