电磁线圈发射器相似模型及模型实验研究
邹本贵,孙学锋,曹延杰,谭乐祖,曾家有
(海军航空工程学院指挥系,山东烟台 264001)
电磁线圈发射器相似模型及模型实验研究
邹本贵,孙学锋,曹延杰,谭乐祖,曾家有
(海军航空工程学院指挥系,山东烟台 264001)
模型实验是研究电磁线圈发射器(EMCL)工作特性的有效方法,要将模型实验结果应用于EMCL原型的研究,必须弄清模型与原型各物理参数间的相似关系。以EMCL数学模型为基础,根据相似理论推导出EMCL相似模型的模型设计条件;对发射器的相似模型进行仿真分析;进行了单级EMCL相似模型实验研究,实验测得的放电回路电流、电枢速度均满足相似模型的模型设计条件。研究结果表明:EMCL各物理参数的相似系数均可由尺度比例系数表示且与尺度比例系数成函数关系;只要给定EMCL原型结构参数和尺度比例系数,可以推导结构相同、尺度不同的EMCL缩比模型的工作特性;也可以根据EMCL缩比模型的结构参数和尺度比例系数反推EMCL原型的工作特性,为模型实验设计奠定了理论基础。
兵器科学与技术;电磁线圈发射器;相似模型;尺度比例系数;模型实验
0 引言
电磁线圈发射器(EMCL)是一种新概念动能武器,具有弹丸和炮管无机械接触、力学结构合理、效率高等诸多优点,特别适合低速、大质量载荷的发射,如导弹、无人机等的弹射,具有广阔的军事应用前景[1-4]。
EMCL发射过程是一个毫秒量级的瞬态高压放电过程,不仅涉及变参数电路中的暂态过程,还涉及急剧变化的动力学过程,彼此又通过磁场紧密耦合在一起[5]。采用全尺寸EMCL进行大载荷的发射实验是非常困难的,而且实验结果往往只能得出个别量之间的规律性关系,难以发现和抓住现象的全部本质,从而无法向实验条件范围以外的同类现象推广[6]。一个替代的方法是EMCL缩比模型实验,由实验得到的结果外推到全比例设备上,可以大幅度减少实验工作量和费用,而且易于实验数据的整理与分析。将EMCL模型实验结果推广到原型实验中,必须要弄清模型与原型各物理参数间的相似关系。
模型实验的理论基础是相似理论,只有掌握并正确运用相似理论的基本原理,才能保证模型实验取得预期结果[6]。相似理论应用于EMCL方面的研究文献较少,主要集中在轨道炮方面[7-10]。美国桑迪亚国家实验室通过模型实验研究EMCL原型的工作特性[11-13];武汉大学对EMCL相似关系进行了研究,推导出了EMCL缩比因数可用尺度比例系数和初始电压的比例系数表示[14]。经过分析发现初始电压的相似系数与尺度比例系数也呈相似比例关系,故本文以EMCL数学模型为基础,根据相似理论推导EMCL相似模型的模型设计条件;利用模型设计条件对EMCL相似模型进行仿真分析;在理论和仿真研究的基础上,开展单级EMCL相似模型的实验验证。
1 EMCL相似模型
1.1 EMCL等效电路
EMCL工作机理是发射线圈中变化的电流产生的磁场与电枢中感应的涡流相互作用产生电磁力推动电枢加速运动。假设电枢沿z轴运动,n级发射线圈依次馈电触发,当第m级(m=1,2,…,n)发射线圈馈电时EMCL发射过程的等效电路如图1所示。
图1中:U0m和Cm是第m级电容器初始放电电压和电容量;Um为t时刻第m级电容器的电压;v是弹丸速度;R0为回路固有电阻(包括电容器电阻、放电开关电阻和接线电阻);L0为回路固有电感(包括电容器电感、放电开关电感和接线电感);Rdm和Ldm分别为第m级发射线圈的电阻和电感;Rp和Lp分别为电枢的电阻和电感;Mdmpm为第m级发射线圈与电枢之间的互感;D为续流硅堆;idm和ipm分别为第m级发射线圈中放电回路电流和电枢中的涡流。
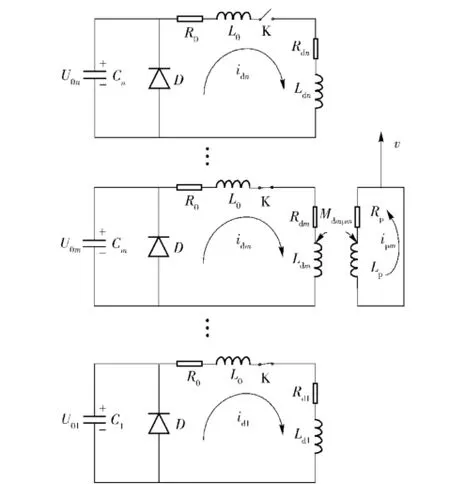
图1 EMCL等效电路Fig.1 Equivalent circuit of EMCL
1.2 EMCL原型与模型
设x表示EMCL原型中的物理量,某一时刻t,当给第m级发射线圈馈电时,EMCL原型等效电路方程为


(4)式~(16)式中:mp为弹丸质量;Fz为电磁力;i为电流;a(t)为弹丸的加速度;y(t)为弹丸运动的距离;η为发射效率;ρ为电阻率;l0为导线长度;A为导线截面积;μ为磁导率;dl1和dl2分别为发射线圈和电枢线圈的等效长度元;r为距离矢量;H是磁场强度;B为磁感应强度;E为电场强度;J为电流密度;σ为电导率;S为应力张量。
设x′表示EMCL模型中的物理量,将x′代入(1)式~(16)式则得到某一时t′,当给第m级发射线圈馈电时EMCL模型的数学模型。
1.3 EMCL模型设计条件
由相似第一定理可知,两个物体的现象相似,其对应物理量互成比例[15],则

式中:cx为物理量x所对应的相似系数。
根据量纲一致性原理将对应物理量相似系数带入(1)式~(16)式并与EMCL模型的数学模型进行比较,消去式中物理量,可得到EMCL各物理量的相似系数关系,即

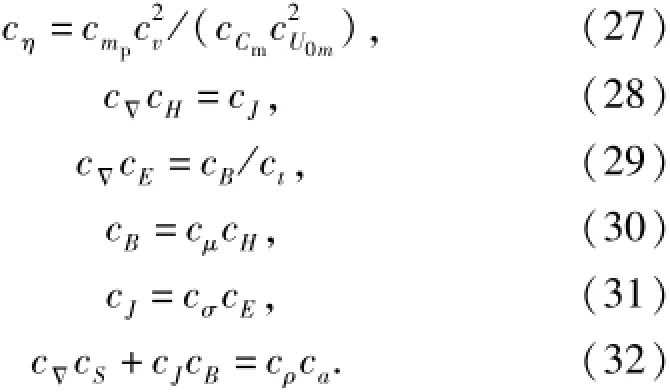
假设在EMCL发射过程中发射线圈和电枢不发生弹塑性变形,同时忽略非线性现象包括:磁扩散、热损失和摩擦产生的影响。假设EMCL尺度比例系数为cl,则cz=cy=cr=cl1=cl2=cl0= cl.假设模型与原型所用材料相同,则cμ=cσ= cρ=ck=1,cmp=cρcV=c3l,其中V为体积。发射线圈匝数N量纲为1,则cN=1.哈密顿算子在直角坐标系中表示为

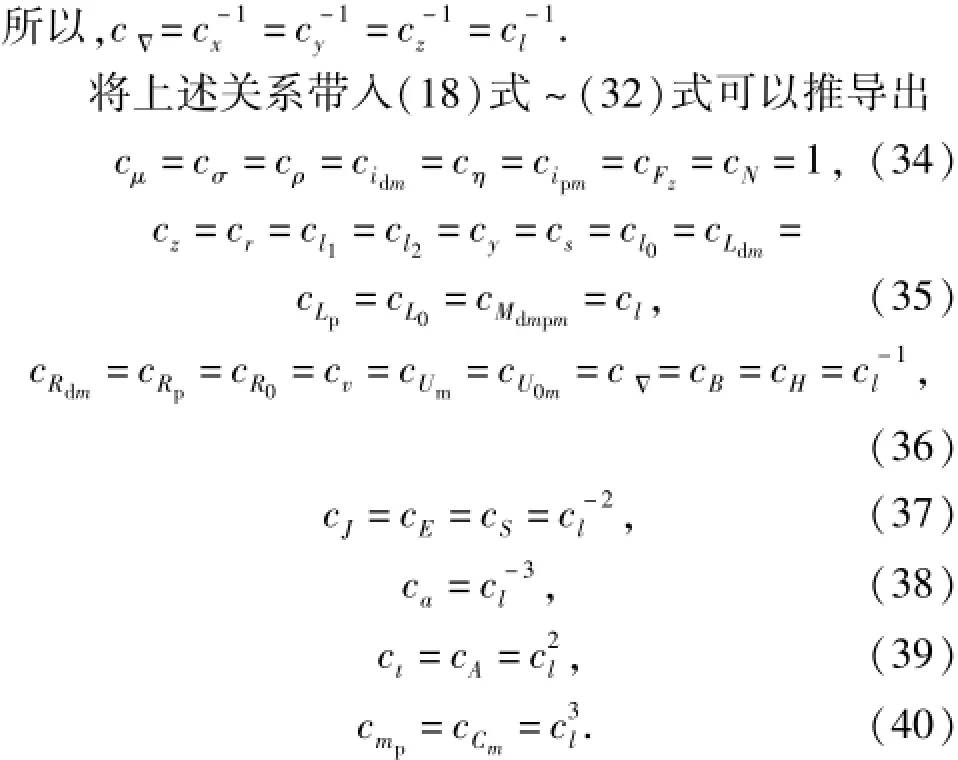
由(34)式~(40)式可知,EMCL各物理参数的相似系数不是任意选择的,它们之间是相互关联的;只要给定了尺度相似系数cl,其他各物理参数的相似系数均可表示为cl的函数。
2 EMCL相似模型仿真
2.1 EMCL模型结构及参数
设计了一种新型EMCL,该发射器模型结构如图2所示。该发射器在电磁线圈发射器的底部加注了一个弹射线圈以提高弹丸进入第1级驱动线圈的速度。为了便于书写,文中弹射线圈和驱动线圈统称为发射线圈,其中i1、i2、i3…in分别为第1级发射线圈(即弹射线圈)、第2级发射线圈(即第1级驱动线圈)、第3级发射线圈(即第2级驱动线圈)、…、第n级发射线圈(即第n-1级驱动线圈)的电流。

图2 新型EMCL模型Fig.2 The new EMCL model
根据EMCL模型与原型各物理参数的相似关系,模型参数与相似比例系数的关系如表1所示。

表1 EMCL相似模型参数Tab.1 Parameters of EMCL scale model
2.2 仿真结果及分析
分别令cl=1(原型)、cl=2、cl=5和cl=10,按照表1中EMCL相似模型参数进行仿真,仿真得出回路电流、电枢受力、弹丸速度及位移随时间的变化规律如图3~图6所示,具体物理参数数值比较如表2所示。这里特别说明图3~图6中横坐标时间轴t″=lgt.
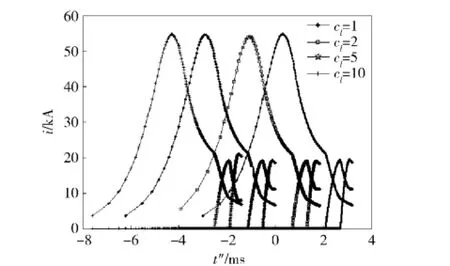
图3 回路电流随时间变化Fig.3 Loop current vs.time

图4 电枢受力随时间变化Fig.4 EM force acting on armature vs.time

图5 弹丸速度随时间变化Fig.5 Projectile velocity vs.time
对10匝的弹射线圈分别按照cl=1和cl=0.2的相似系数进行有限元仿真,加载的电流波形如图3所示。仿真得出弹射线圈的磁场、应力和变形随尺度比例系数的变化规律如图7~图9所示,电枢的涡流密度、应力和变形如图10~图12所示,具体物理量数值比较如表2所示。

图6 弹丸位移随时间变化Fig.6 Projectile displacement vs.time

表2 物理参数值比较Tab.2 Comparison of physical quantity values
由图3~图12和表2~表3可以看出,根据尺度比例系数cl建立的EMCL模型的物理参数是可以用cl表示的且与cl是成比例关系的。只要给定原型结构参数和尺度比例系数cl,可以研究与之结构相同、尺度不同的EMCL模型的工作动态特性;反之,可以根据EMCL缩比模型的结构参数和尺度比例系数cl反推EMCL原型的工作动态特性,这为模型实验的设计奠定了理论基础。

图7 弹射线圈磁场随尺度比例系数的变化Fig.7 The catapult coil distributions of magnetic flux density vs.cl
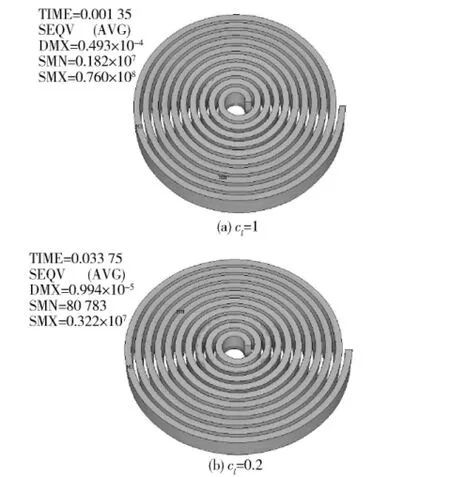
图8 弹射线圈应力随尺度比例系数的变化Fig.8 Catapult coil Von Mises stress vs.cl
3 相似模型实验验证
3.1 实验参数
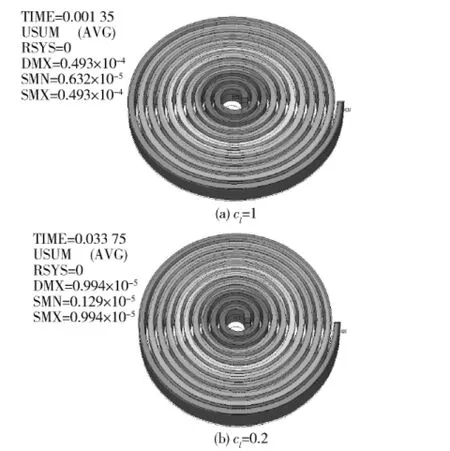
图9 弹射线圈变形随尺度比例系数的变化Fig.9 Catapult coil deformation vs.cl

图10 电枢涡流密度随尺度比例系数的变化Fig.10 Armature eddy current density vs.cl
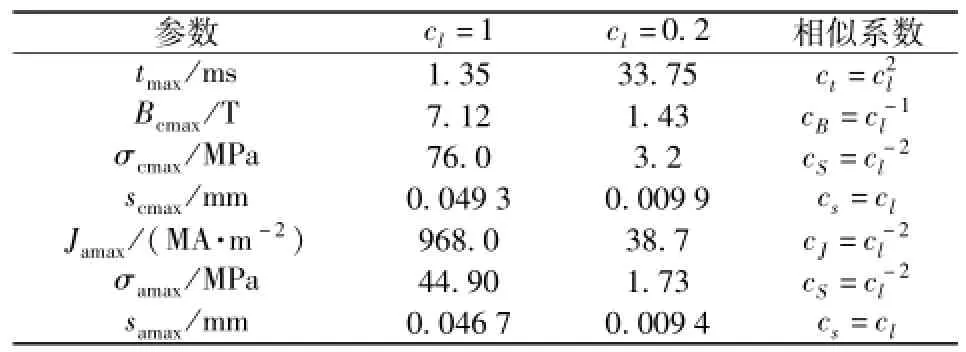
表3 单级EMCL有限元仿真结果比较Tab.3 Comparison of FEM simulation resultsof single-stage EMCL
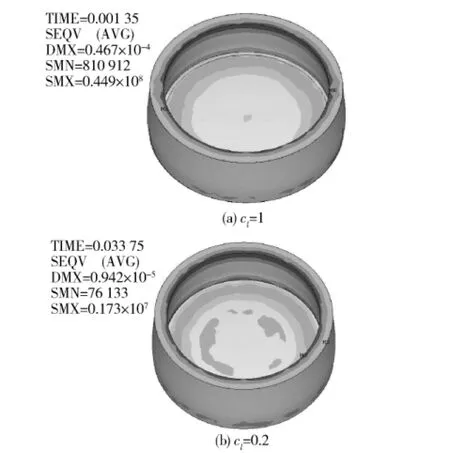
图11 电枢应力随尺度比例系数的变化Fig.11 Armature Von Mises stress vs.cl
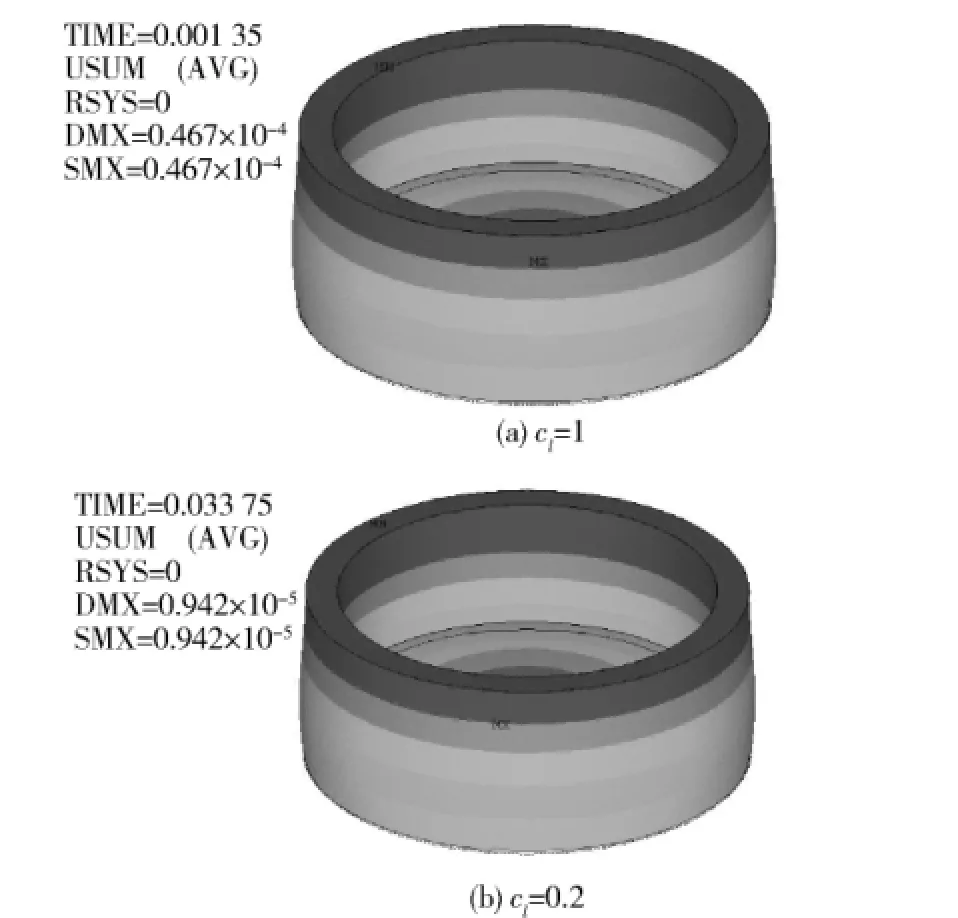
图12 电枢变形随尺度比例系数的变化Fig.12 Armature deformation vs.cl
根据EMCL相似模型的模型设计条件,并考虑到实际加工过程中的条件限制,以尺度比例系数为3∶4制作的弹射线圈和电枢如图13和图14所示。弹射线圈和电枢的结构参数以及实验时外置电路参数如表4所示。
3.2 实验结果及分析
分别对EMCL模型1和模型2进行了3次放电实验,测量得到一组模型1和模型2的回路电流,如图15和图16所示,电枢经过网靶的时间如图17和图18所示。通过计算得出6次发射实验的实验结果如表5所示。

图13 弹射线圈Fig.13 Catapult coils

图14 电枢Fig.14 Armatures

表4 实验装置的结构参数和电路参数Tab.4 Structure and circuit parameters of experimental devices
由表5可以看出,实验中测量得到的模型1和模型2的回路电流相差很小。随着发射次数的增加,回路电流逐渐减小,这说明回路电流产生的热量导致线路电阻增大,所以随着发射次数的增大,回路电流变小,如果忽略温升对回路电阻的影响,可以认为两个模型中的回路电流近似相等,即证明ci=1.模型1经过3次发射后电枢的平均速度为26.7 m/s,模型2经过3次发射后电枢的平均速度为20.3 m/s,

图15 模型1回路电流信号Fig.15 The loop current measured in Model 1

图16 模型2回路电流信号Fig.16 The loop current measured in Model 2

图17 模型1测得的时间信号Fig.17 The time measured in Model 1

图18 模型2测得的时间信号Fig.18 The time measured in Model 2
v1/v2=26.7/20.3=1.32;模型1和模型2的尺寸比例为3/4,即:l1/l2=3/4.根据EMCL相似模型中的结论cv=,有v1/v2=/l=l2/l1=4/3=1.33,与实验结果v1/v2=1.32基本相符,这说明实验结果与理论分析结果基本相符。

表5 实验结果Tab.5 Experimental results
4 结论
以EMCL数学模型为基础,根据相似理论推导出了EMCL相似模型的模型设计条件。只要给定原型结构参数和尺度比例系数cl,就可以研究与之结构相同的EMCL模型的工作动态特性。同样,可以根据EMCL模型的结构参数和尺度比例系数cl反推EMCL原型的工作动态特性。进行了单级EMCL相似模型验证实验,实验测得的放电回路电流、电枢速度均满足相似模型的模型设计条件,有效验证EMCL相似模型的正确性。
References)
[1] Kaye R J,Tuman B N,Shope S L.Applications of coilgun electromagnetic propulsion technology[J].IEEE Transactions on Magnetics,2002,38(1):703-707.
[2] Lockner T R,Kaye R J,Tuman B N.Coilgun technology,status, applications,and future directions at Sandia National Laboratories [J].IEEE Transactions on Magnetics,2004,40(1):119-121.
[3] Burps T J,Cnarc E C,Obcrkampf W L,et al.The electromagnetic θ gun and tubular projectiles[J].IEEE Transactions on Magnetics,1982,18(1):46-59.
[4] 王莹,肖峰.电炮原理[M].北京:国防工业出版社,1995:96-97.
WANG Ying,XIAO Feng.Theory of electric gun[M].Beijing: National Defense Industry Press,1995:96-97.(in Chinese)
[5] 张海燕.线圈炮电磁过程动态仿真技术研究[D].哈尔滨:哈尔滨理工大学,2005.
ZHANG Hai-yan.The dynamic simulation of electromagnetic process in coilgun[D].Harbin:Harbin University of Science and Technology,2005.(in Chinese)
[6] 袁文忠.相似理论与静力学模型试验[M].成都:西南交通大学出版社,1998:7-8.
YUAN Wen-zhong.Similarity theory and statics model experiments [M].Chengdu:Southwest Jiaotong University Press,1998:7-8. (in Chinese)
[7] James T E.Efficiency,performance limits and scaling of rail launchers[J].IEEE Transactions on Magnetics,1999,35(1): 403-408.
[8] Hsieh K T,Kim B K.One kind of scaling relations on electromechanical systems[J].IEEE Transactions on Magnetics,1997, 33(1):240-244.
[9] Satapathy S,Vanicek H.Energy partition and scaling issues in a railgun[J].IEEE Transactions on Magnetics,2007,43(1): 178-185.
[10] Yun H D.EM gun scaling relationships[J].IEEE Transactions on Magnetics,1999,35(1):484-488.
[11] Aubuchont M S,Lockner T R,B N Turman.Results from Sandia National Laboratories/Lockheed Martin electromagnetic missile launcher(EMML)[J].IEEE Transactions on Magnetics,2005, 41(1):75-78.
[12] Padilla M.Sandia,Lockheed Martin develop electromagnetic missile launcher for naval shipboard operations[J].Sandia Lab News,2005,57(2):1-4.
[13] Skurdal B D,Gaigler R L.Multi-mission electromagnetic launcher[J].IEEE Transactions on Magnetics,2009,45(1):458-461.
[14] ZHANG Ya-dong,WANG Ying,RUAN Jiang-jun.Capacitor-driven coil-gun scaling relationships[J].IEEE Transactions on Plasma Science,2011,39(1):220-224.
[15] 谭庆明.量纲分析[M].合肥:中国科学技术大学出版社, 2005:17-18.
TAN Qing-ming.Dimensional analysis[M].Hefei:University of Science and Technology of China Press,2005:17-18.(in Chinese)
Scale Model and Model Experiment of Electromagnetic Coil Launcher
ZOU Ben-gui,SUN Xue-feng,CAO Yan-jie,TAN Le-zu,ZENG Jia-you
(Department of Command,Naval Aeronautical and Astronautical University,Yantai 264001,Shandong,China)
Model experiment is an effective method to investigate the working process of electromagnetic coil launcher(EMCL).The model experiment results are used for prototype study of EMCL after the scaling factor relations of the physical parameters of model and prototype are mastered.Based on mathematical model of EMCL and similarity theory,the requirements for designing the model of EMCL are derived.The scaling model is researched by simulation.The experiment verification of the single-stage EMCL is conducted.The simulation of EMCL and experimental results show that the scaling factor relations of physical parameters are expressed as functions of the length scale factor.The working characteristics of EMCL sub-scale model can be deduced if the structure parameters of EMCL prototype and the length scale factors are given,and vice versa.The research results lay the theoretic foundation for model experiment.
ordnance science and technology;electromagnetic coil launcher;scale model;length scale factor;model experiment
O 303;TM866
:A
1000-1093(2014)05-0733-08
10.3969/j.issn.1000-1093.2014.05.023
2013-03-11
国防预先研究项目(9140A25070208JB1402)
邹本贵(1981—),男,讲师。E-mail:se-sky@163.com

