感应电机无传感器矢量控制系统中的参数静止辨识

郑爱莲，徐枝新

（1.国家电网温州供电公司电力调度中心，浙江温州325000；2.浙江科技学院理学院，浙江杭州310023）

1 引言

感应电机无速度传感器矢量控制（SVC）由于免去了速度传感器带来的麻烦，提高了系统可靠性，降低了系统成本，因此受到了国内外学者广泛而深入的研究［1-3］。目前，该项控制技术已成为通用恒转矩应用的选择，基本上所有的低压通用变频器厂家以及部分高压变频器厂家都提供该技术模式。虽然实现无传感器控制的方法很多，但是它们在转速估算时都用到定/转子电阻、漏感及互感等电机参数。众所周知，电机参数对低频段（额定转速的10%以下）矢量控制系统性能影响较大［4］，因此为了改善低速性能大多数矢量控制变频器采用传统的空载和堵转测量电机参数。但是很多场合负载和电机已经连接，且不能拆卸或很难拆卸时，就要求变频器能够在电机不转动的情况下精确辨识电机参数。目前，国内外有些品牌的变频器同时提供参数静止自辨识和旋转自辨识两种选择，如日本安川变频器、深圳蓝海华腾变频器、正弦SINE变频器等。但是这些变频器在产品说明书中都注明如果用在控制精度较高的场合，用户必须采用旋转法辨识电机参数。

在电机参数辨识中，定子电阻、漏感的辨识方法相对简单且容易获得与实际相近的值，而转子电阻、互感的辨识较为困难，不同的方法测出的数值偏差较大。文献［5］采用一种自适应算法对误差电压进行补偿提高了参数辨识精度，文献［6］采用双低频电流激励法并利用解方程的办法同时得到了互感和转子电阻值。

本文在感应电机T 型等效模型基础上，给出了电机静止状态下定转子电阻、漏感、互感的辨识方法。利用通用变频器平台进行参数辨识，并把辨识出来的参数用于无传感器矢量控制系统中，变频器优异的低速性能表明参数辨识是准确的。

2 静止法电机参数辨识

静止状态下感应电机的T型等效模型如图1所示，其中，Rs为定子电阻，Rr为转子电阻，L1s，L1r为定、转子漏感，Lm为互感，I为电机相电流，U为电机相电压。

图1 静止状态下感应电机的等效模型Fig.1 Equivalent model of induction motor at standstill

2.1 定子电阻的辨识方法

通常定子电阻采用简单的直流伏安法就可测得，也就是在电机任意两相绕组间通低压直流电，测量绕组上的电压U 和通过绕组电流I 的大小。在低压变频器中，获得低压直流电的方法是对数百伏的直流母线电压进行斩波，斩波得到的高频脉冲经过定子绕组的电感滤波后就变成一个脉动很小的直流电了。电压源型变频器和电机系统如图2所示。

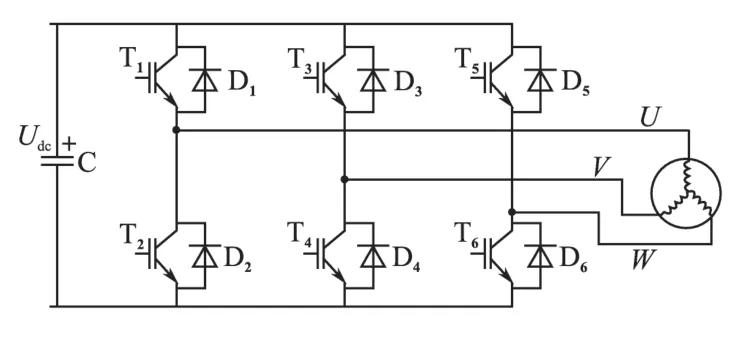
图2 电压源型变频器和电机系统Fig.2 Voltage source inverter for motor drives

在图2 中使T1一直导通，T2，T3，T5，T6一直关断，而T4采用PWM调制，则在电机UV相间产生1个单向电压脉冲序列。Ts为1个PWM周期，脉冲宽度为t，则脉冲占空比D=t/Ts，绕组上的电压平均值等于D·Udc，这时的定子电阻值为

由于测量定子电阻时等效电压很低，这时IGBT的导通压降UIGBT和续流二极管的导通压降UDIODE都不能忽略。当T4导通时，电流将流经2个IGBT，这时加在电机UV相电压为Udc-2·UIGBT；当T4截止时，电流将流经1个IGBT和1 个续流二极管，这时加在电机UV相的电压为-(UIGBT+UDIODE)。这样，UV绕组上得到的直流电压平均值应为

考虑IGBT 导通、关断延时，式（2）中的占空比D=(t-ton+toff)/Ts。通常设UIGBT=UDIODE，则式（2）可以简化为

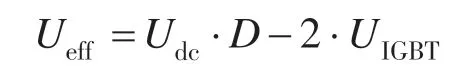
为了消除死区、管子开关延时、管子压降给定子电阻测量带来的影响，一般取2个不同的占空比，得到定子电阻值：

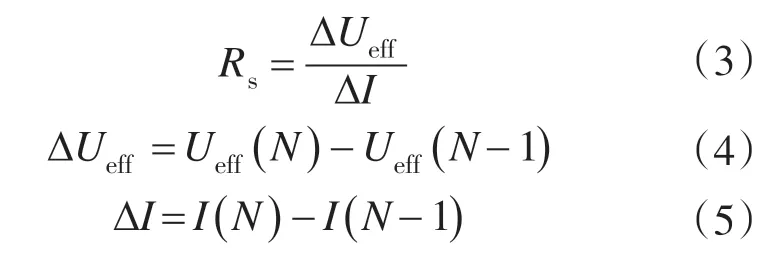
式中：Ueff(N)，Ueff(N-1)分别为第N，N-1 个电压有效值；I(N)，I(N-1)分别为第N，N-1个电流值。最后对得到的N-1个电阻值作算术平均，从而提高测量的精度。

2.2 漏感的辨识方法

通常漏感和转子电阻的测量都采用三相堵转法，但实际上堵转比较困难，因此采用单相短路试验代替三相堵转。当电机加上单相正弦电压时，没有电磁转矩产生，其电磁现象与三相堵转基本相同。图3为电机忽略励磁阻抗时的等效模型。

图3 堵转时的感应电机等效模型Fig.3 Equivalent model of induction motor at stall

图2 中，T5，T6一直关断。相位在0-π时，T1导通，T2，T3关断，T4采用SPWM 调制；相位在π-2π时，T2导通，T1，T4关断，T3采用SPWM 调制。由于电感的滤波作用，可以认为在UV端加了正弦电压。当电流达到稳定值后，选择电压相位为零的时刻对电流进行采样，存储一个周期的电流采样值，经快速傅里叶变换（FFT）得到Imsinφ和Imcosφ，其中：Im为电流基波幅值，φ为电流对电压的相位滞后。一般地，认为定子漏感与转子漏感相同，则有：

式中：Um为电压基波幅值；ω为基波频率。

为了降低励磁阻抗对测量的影响，ω一般取电机额定频率ωe的2～3倍。

2.3 转子电阻的辨识方法

在堵转实验中，正弦基波频率f 大小对辨识转子电阻的影响很大。考虑到实际运行中转子电流频率很低（等于转差频率），因此本文测转子电阻的交流电流信号频率一般取在电机的额定转差频率附近。电机这时每相的等效阻抗非常小，为了保证变频器、电机不过流，基波电压幅值通常只能取几V～几十V。在这种情形下，死区对基波电流的影响非常大。实验表明：如果不补偿死区，则经过FFT 后的基波电流幅值Im偏小，计算出转子电阻偏大；如果死区过补偿，那么FFT 提取的基波电流幅值Im偏大，导致计算的转子电阻偏小。由于每台变频器功率器件电气参数不可能一致，外围硬件电路也不相同，所以从理论上推导死区补偿公式是有困难的。经过本实验组数年的实践，发现补偿死区设定值的50%～70%比较适合。比如死区设定为2.5 μs，则实际死区补偿量取在1.25～1.75 μs 之间。利用FFT 法先求出定转子总电阻值，然后减去已经辨识的定子电阻值，就可以得到转子电阻值，计算公式如下：

2.4 互感的辨识方法

在定转子电阻、漏感都已辨识的情况下，利用图4 所示的电机Γ型等效模型就可以在静止条件下实现互感的辨识。Г型等效电路中的参数与T型等效电路的对应关系为

图4 电机Γ型等效模型Fig.4 Γ-model of induction motor

互感两端电压变化伴随着磁链的变化，设互感L′m两端电压为U，产生的等效磁链为Ψ′，它与磁链的关系为

若给单相绕组通入低频阶跃电压，由于电感的存在电流会经历缓慢的过渡过程，只要阶跃电压的周期足够长电流就可以进入稳态，见图5。

图5 低频方波激励与电流响应Fig.5 Low-frequency excitation and current response

若选择一个周期开始时刻作为t1，半周期结束时刻作为t2，且t1和t2处的电流均已进入稳态Im，那么，因此有

上式离散化为

3 实验验证

无速度传感器矢量控制特点之一就是低速区带载能力、转速精度对电机参数较敏感，因此把辨识出的参数应用于无传感器矢量控制，通过观测电机的低速带载能力、转速精度来判断参数辨识的正确性。实验用异步电机铭牌参数为：型号Y2-00P 180L-4，额定功率30 kW，额定转速1455 r/min，功率因数0.85，4 极，三角形接法，额定电流58.9 A。无传感矢量控制采用全阶自适应状态观测器观测磁链和转速估计［7］，无速度传感器矢量控制系统框图如图6所示。其中，AΨR为磁链PI调节器，ASR为转速PI调节器，2个AIR分别是励磁电流PI 调节器、转矩电流PI 调节器，usdc，usqc为d，q轴电压交叉解耦分量。

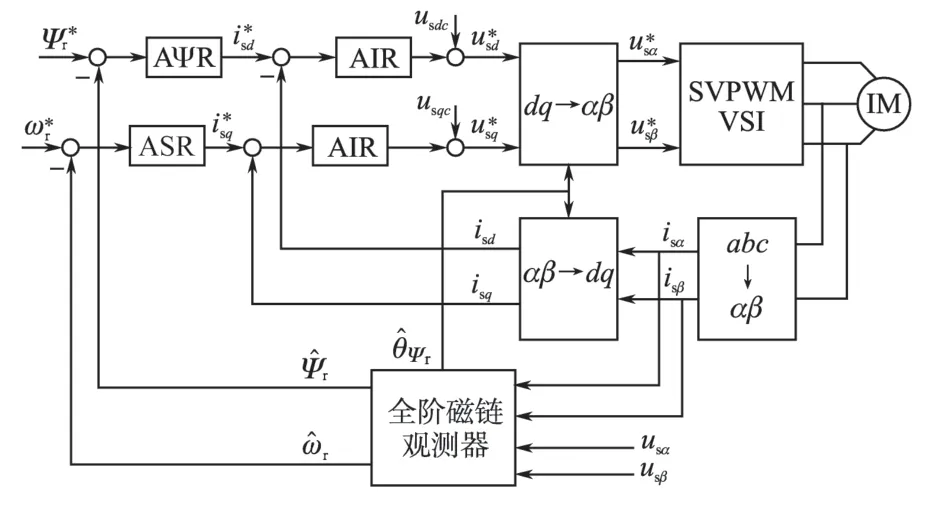
图6 基于全阶磁链观测器的无速度传感器矢量控制系统框图Fig.6 Block diagram of sensor-less vector control system using full-order observer

参数辨识和无速度矢量控制算法采用主频150 MHz 的TMS320F2812 DSP 来实现，PWM 调制频率为5 kHz，死区时间为2.93 μs。为确保系统的可靠性，除DSP核心板自制外，其余硬件均借助30 kW的通用变频器。带载采用2台相同型号的异步电机进行对拖，即作为负载的电机用带测速编码器矢量变频器控制并设为转矩模式，无速度算法控制的变频器则处于转速模式。型号为Y2-00P 180L-4的实验电机参数辨识结果见表1。

表1 电机参数辨识结果Tab.1 Identification of motor parameter

表1 中同时给出了空载法（电机运行频率40 Hz）测出的互感值。从表1 可以看出，静止法测出的互感值略高于空载法，原因是死区补偿有些不足，导致实测电流偏小，感抗变大。取5次测量值的算术平均，则型号为Y2-00P 180L-4 的实验电机参数为：定子电阻0.097 5 Ω，转子电阻0.085 Ω，定转子漏感0.8 mH，互感36.2 mH。最后，把辨识出的电机参数应用到图6 所示的全阶磁链观测器无传感矢量控制系统中。图7是工作频率分别为0.5 Hz，1 Hz，5 Hz 带150%额定负载时的电机线电流波形，电流正弦度很好，没有畸变。通过负载电机上的测速编码器可以得到，工作频率为0.5 Hz，1 Hz，5 Hz 时，实际运行频率分别为0.59 Hz，1.09 Hz，4.96 Hz。

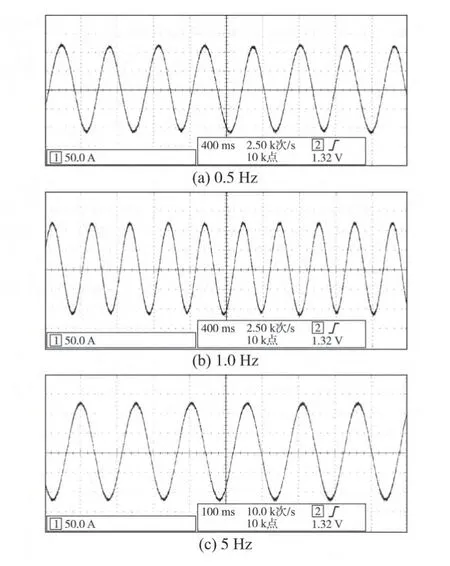
图7 150%额定转矩下电机线电流波形Fig.7 Current waveforms of motor at rated torque 150%

4 结论

本文针对变频器的实际工况提出了一套感应电机静止情况下的参数测量方法。通过无传感器矢量控制低速带载能力和转速精度的测试，证明参数辨识是比较准确的。考虑到定转子电阻随温度、电流等因素影响较大，要长时间保证无速度条件下的带载和转速精度，还是需要做到参数的在线辨识，这个问题在今后研究中着重解决。

［1］Joachim H，Juntao Q.Sensorless Vector Control of Induction Motors at Very Low Speed Using a Nonlinear Inverter Model and Parameter Identification［J］.IEEE Transactions on Industry Applications，2002，38（4）：1087-1095.

［2］付能.感应电机无速度传感器变频调速系统研究［D］.武汉：华中科技大学，2009.

［3］郑泽东，李永东，Maurice F.采用Kalman滤波器进行信号处理的高频信号注入法在电动机控制中的应用［J］.电工技术学报，2010，25（2）：54-59.

［4］Toliyat H A，Emil L，Mona R.A Review of RFO Induction Motor Parameter Estimation Techniques［J］.IEEE Transactions on Energy Conversion，2003，18（2）：271-283.

［5］陈伟，于泳，徐殿国，等.基于自适应补偿的异步电机静止参数辨识方法［J］.中国电机工程学报，2012，32（6）：156-162.［6］杨光，徐政，陈锐坚.感应电机参数静止辨识的误差特性分析［J］.电气传动，2013，43（2）：7-10.

［7］罗慧.感应电机全阶磁链观测器和转速估算方法研究［D］.武汉：华中科技大学，2009.