永磁直驱同步风力发电机滑模控制研究

刘军，吴琼

（西安理工大学自动化学院，陕西西安710048）

1 引言

风力发电系统可以分为两大类：恒速恒频［1］与变速恒频［2］发电系统。为了在宽广的风速变化范围内实现最大风能捕获，变速恒频机组应运而生。主流的变速恒频机组可以分为：基于双馈感应发电机和基于永磁同步发电机的直接驱动机组两类。随着电力电子器件的飞速发展以及价格的不断降低。从长远来看永磁直驱风力发电系统将会成为风力发电技术领域的重要发展方向［3］。本文主要讨论背靠背双PWM 拓扑结构的永磁直驱风力发电系统。

永磁同步风力发电机是一个多变量、强耦合、非线性的变参数复杂对象［4］，常规的PI 控制无法在系统参数变化以及外加干扰时满足高性能控制要求，并且PI控制易产生超调。为了解决上述问题，非线性控制被逐渐引入，例如神经网络控制［5］模糊控制［6］等。神经网络控制的控制效果过分依赖学习样本的质量和数量，且不易工程实现。模糊控制虽然可以改善超调但是会存在稳态误差，控制效果有限［6］。滑模变结构控制因其对模型精度要求不高，对参数摄动、外部扰动具有强鲁棒性等优点而受到越来越多的关注［7］。文献［8］把转速环和电流环结合成一个整体，设计了滑模控制器，并且采用常规指数趋近律减小抖振。常规指数趋近率的切换带为带状，系统最终不能趋近于原点而是趋近于原点的抖振，这可能激发系统的未建模高频分量。

为了简化控制保证电流的快速性，文献［9］将转速环PI控制器换为滑模控制器，将滑模控制器与PI 控制器结合起来。文献［10］采用新型趋近律克服了指数趋近律在滑模切换带上为带状的缺点。

为了简化控制保证电流的快速响应，本文转速环采用滑模控制器代替传统PI控制器，并且采用变速变指数趋近律，更好地减小抖振并且加快趋近速度，在削减抖振的同时，为了提高系统的鲁棒性。对滑模增益进行了分段设计。在Matlab/Simulink 环境下进行了仿真，仿真结果表明采用本文提出的基于变增益变速变指数趋近律的滑模变结构永磁同步风力发电机控制策略系统可以无超调地跟踪给定转速，并且响应速度快，转矩冲击小，系统鲁棒性强。

2 永磁同步风力发电系统最大风能跟踪控制

永磁同步风力发电系统首先将风能转化为旋转的机械能，然后发电机将机械能再转化为电能并入电网。

风力机的机械转矩可以表示为

由Pω=Tω×ω，可以得到相应的机械功率：

式中：ω为风轮的角速度，rad/s；R为风轮半径，m；v 为上游风速，m/s；Cp为风能利用系数；λ为叶尖速比；β为节距角。

叶尖速比的公式为

由式（2），式（3）可以得到如下结论：当风速一定时，风机所获得的机械功率与风能利用系数成正比。当风能利用系数取最大值时，风机获得的风能最大。在定桨距情况下风能利用系数只与叶尖速比有关，与风速的大小无关。Cp常用的近似计算公式如下［11］：

由式（4），式（5）可以得到定桨距角情况下叶尖速比与风能利用系数的关系如图1所示。

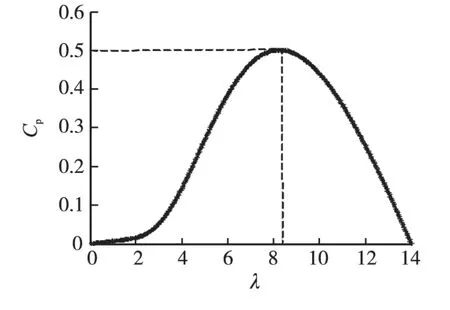
图1 Cp—λ关系曲线Fig.1 Relationship betweenCp—λ

由图1可以看出，Cp随着λ的变化而变化。大约在λ=8.1，Cp最大值接近0.5。由此可见无论在不同风速下，只要保持λ=λopt，就能维持风力机在Cpmax下运行，即保持风力机获得机械功率最大。所以在风速变化时，通过调整风力机的转速，可以使风力机工作在最佳叶尖速比状态下，实现最大风能跟踪［12］。

3 永磁同步风力发电机滑模变结构控制策略

3.1 永磁同步风力发电机数学模型

为了便于对永磁同步风力发电机进行分析，在建模时做如下假设［5］：

1）忽略空间谐波，设电机中是对称三相绕组，在空间互差120°（电角度）。输出三相正弦交流电相互对称；

2）忽略磁路饱和和铁心饱和，忽略整个系统电机中涡流及磁滞损耗的影响；

3）转子及安装在转子上的永磁体没有阻尼作用；

4）所产生磁动势沿气隙变化规律呈正弦分布；

5）不考虑频率及温度变化等外界因素对永磁体和绕组产生的影响。

经过坐标变换，PMSG 在dq 坐标系下，定子电压方程、磁链方程和电磁转矩方程分别如下式：

式中：ud，uq为定子电压在dq 轴上的分量；id，iq为定子电流在dq 轴上的分量；ψd，ψq为磁链在dq 轴上的分量；Ld，Lq为等效dq 轴电感；ψf为永磁体磁链。

把风力机与永磁同步发电机看作一个整体，其机械运动方程可以写为

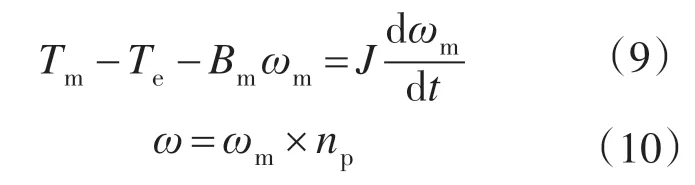
式中：Tm为风力机机械转矩；Te为永磁同步发电机电磁转矩；Bm为转动粘滞系数（在理想的状态下一般取值为零）；np为发电机极对数；ωm为风力机机械角速度（由于是直驱系统，所以其值与发电机机械角速度相等）；ω为发电机电角频率。

3.2 变增益变速变指数控制器设计

将旋转坐标系下永磁同步风力发电机改写为如下状态方程：

滑模控制的核心是找到一个控制量，通过控制量的切换使系统状态沿着滑模面滑动，使系统在受到外部干扰和参数摄动的时候具有不变性。通常滑模控制器的设计分3个步骤：

1）根据所给系统选择合适的滑模面；

2）计算控制量u；

3）验证滑模运动的稳定性。以下将详细介绍变增益变速变指数滑模控制器的设计。

3.2.1 滑模面设计

设滑模变结构控制器的输入为转速误差，输出为q轴电流的给定值。取系统状态变量为

式中：ω*为转子电角速度给定值；ω为发电机实际电角速度。

由式（10）、式（12）可得：

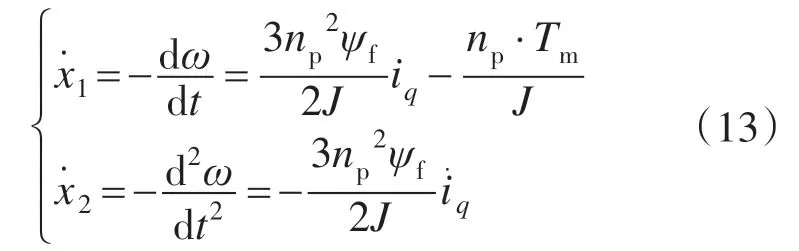
则上式可改写为如下状态方程：

不失一般性，为了使系统无超调达到稳定，选择一阶滑模面为

在滑模控制中滑模面参数c 满足Hurwitz 多项式，这里c>0，对s求导，则有：

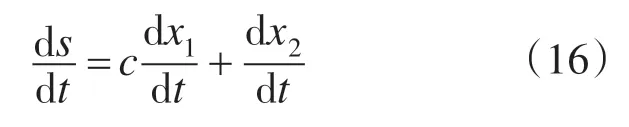
结合式（13）可以得出：

3.2.2 滑模控制率求取

滑模控制最大的缺点就是存在抖振问题。在各种抗抖振方法中趋近律方法相对比较简单，应用广泛［8］。指数趋近律表示如下：

其中，常数ε为系统的运动趋于切换面s=0 的速率；-ks为指数项，趋近速度从一个较大值逐步减小到零。但是单纯的指数趋近，运动点逼近切换面是一个渐进过程，不能满足滑模控制的可达性条件，切换面上也就不存在滑动模态了。因此增加了等速趋近项，当s→0 时，趋近速度是ε，可以保证切换面以外的点在有限时间达到切换面［13］。

指数趋近律虽然可以在一定程度上削弱抖振，但是由于切换带为带状，系统在切换带中向原点运动时，不能趋于原点而是趋于原点的一个抖振，这一现象可能引发系统未建模高频成分［11］。

为了解决这一问题，本文采用变增益、变速、变指数趋近律。此趋近律表示式如下：

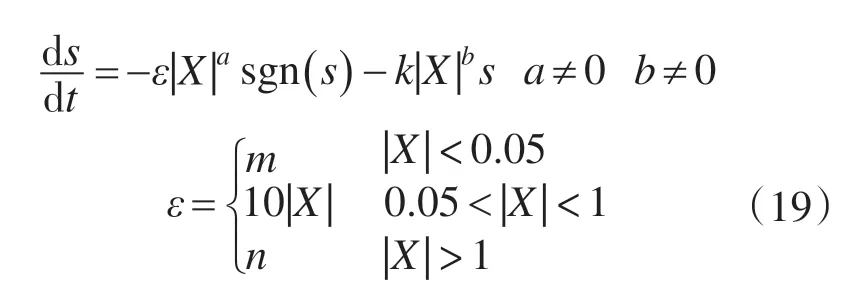
式中：a，b取值范围为1～4；X为引入的系统状态变量，为了避免趋近律中有微分项选择X=x1［13］，在本文为转速误差；m，n 为根据系统参数经过试验效果确定的。

采用变增益变速变指数趋近律，系统状态在远离滑模面时，可以加快状态变量的趋近速度。当接近滑模面时，系统进入切换带，此时穿越滑模面的速率与转速误差的幂函数成正比，因此幅度将越来越小，在理想情况下会稳定于原点，控制效果得到优化。另外滑模增益在系统状态量的不同区间采取分段赋值，可以大幅度削弱抖振，同时依然使系统具有较强的鲁棒性。

将式（19）代入式（17），可得：

3.2.3 稳定性分析

选择李雅普诺夫函数为：V=0.5s2。滑模控制要满足李雅普诺夫稳定性，则应有：

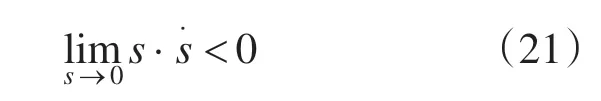
将式（15）、式（19）代入式（21）有：

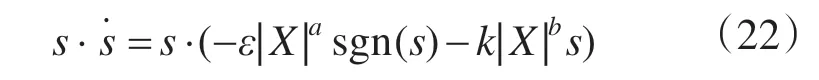
式中：k，ε均为大于零的常数，系统状态变量的幂函数也是大于零的常数，当s大于零时符号函数sgn（s）为正可以保证s导数是小于零的；当s小于零时，符号函数sgn（s）为负可以保证s导数是大于零的，从而满足了稳定性条件。

结合上述控制方案，基于变增益、变速、变指数趋近律的永磁直驱同步风力发电系统，机侧滑模控制系统结构框图如图2所示。

图2 永磁直驱同步风力发电机侧系统滑模控制总体框图Fig.2 Sliding mode control system of permanent magnet synchronous direct-drive wind power system

4 仿真与分析

本文基于Matlab/Simulink，构建了永磁同步风力发电系统机侧矢量控制仿真模型。并用上述基于变增益变速变指数趋近律的转速控制器代替传统矢量控制中的PI控制器。

风力机参数为空气密度ρ=1.225 kg/m2，风机半径R=31 m，桨距角β=0°。永磁同步风力发电机参数：定子电阻0.11 Ω，定子电感2e-4 L，极对数102，磁体磁通1.28 Wb，转动惯量1e3 kg·m2，粘滞系数0 N·m·s

仿真中风速模拟实际风场中风速的变化，风速在0.15 s由6 m/s跃升到8 m/s，再经过0.15 s阶跃到10 m/s。按照最大风能跟踪算法计算出对应的风力机转角速度的给定值分别为1.57 rad/s，2.09 rad/s，2.61 rad/s。

传统PI 控制与基于变增益变速变指数趋近律控制永磁同步风力发电机转速仿真曲线、定子三相电流仿真曲线以及转矩仿真曲线分别如图3～图8所示。

从仿真结果可以看出基于变增益变速变指数趋近律的滑模变结构控制永磁同步风力发电系统可以无超调地跟踪给定转速，并且响应速度快，转矩冲击小，系统鲁棒性强，参数选定方便容易。

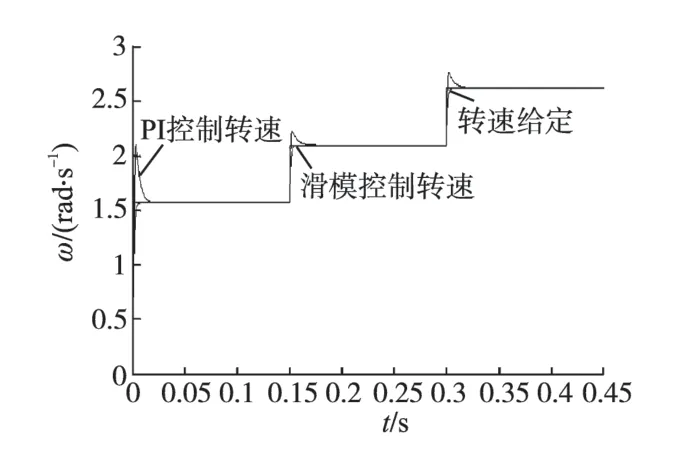
图3 风速变化时PI控制与滑模控制转速对比Fig.3 Compare of PI control and sliding mode control under variable wind

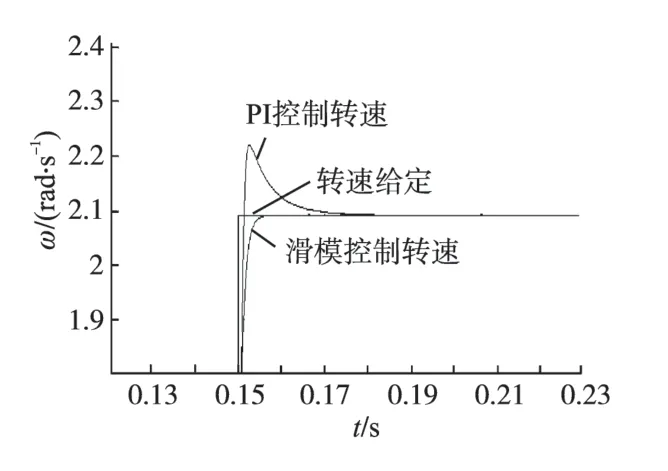
图4 风速为8 m/s时的PI控制与滑模控制的放大图Fig.4 Enlarge figure of PI control and sliding mode control of wind speed 8 m/s

图5 风速变化时PI控制下三相定子电流Fig.5 Three phase stator current of PI control under variable wind

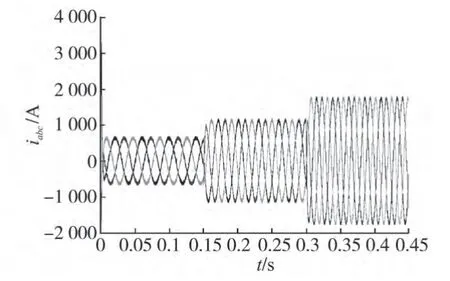
图6 风速变化时滑模控制下三相定子电流Fig.6 Three phase stator current of SMC control under variable wind

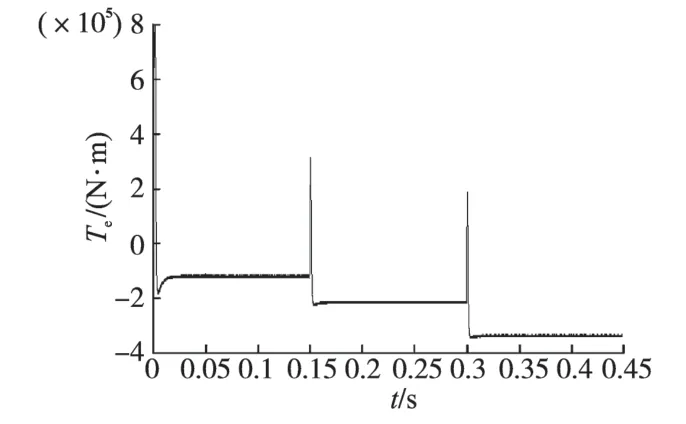
图7 风速变化时PI控制下发电机转矩Fig.7 Motor torque of PI control under variable wind

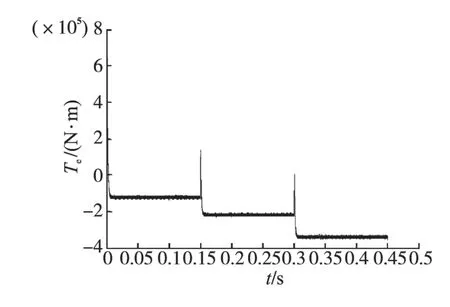
图8 风速变化时滑模控制下发电机转矩Fig.8 Motor torque of SMC control under variable wind

5 结论

本文针对永磁同步风力发电机矢量控制存在PI控制参数整定复杂，在外界扰动及内部参数变化下易产生超调，以及常规滑模控制存在的抖振问题，提出了一种基于变增益变速变指数趋近律的滑模转速控制策略的永磁同步风力发电机最大风能控制方案，设计了变增益变速变指数趋近律的滑模转速控制器。基于Matlab/Simulink构建了永磁同步风力发电机最大风能跟踪仿真模型，分别对常规矢量控制和基于变增益变速变指数趋近律的滑模变结构控制器的永磁同步风力发电机最大风能跟踪控制进行了仿真，仿真验证了改进控制策略是有效的。

［1］李建林，许洪华.风力发电中的电力电子变流技术［M］.北京：机械工业出版社，2008.

［2］吴晓丹，王宇，杨浩，等.变速恒频双馈风力发电系统控制研究［J］.电气传动，2012，42（2）：17-21.

［3］Polinder H，Van Der P，Frank F A.Comparision of Direct-drive and Geared Generator Concepts for Wind Turbines［J］.IEEE Transactions on Energy Conversion，2006，21（3）：725-733.

［4］陈伯时.电力拖动自动控制系统［M］.第4 版.北京：机械工业出版社，2009.

［5］任艳峰，毛开富，包广清.基于神经网络的直驱风力发电最大风能控制研究［J］.电气自动化，2009，31（6）：42-45.

［6］李小华.直驱风力发电网侧变流控制系统的研究与开发［D］.长沙：湖南大学，2009.

［7］朱家厅，王莉娜，薛飞.永磁同步电机的滑模PI模糊逻辑控制［J］.电气传动，2013，43（7）：43-48.

［8］王志宇，王长松，范普成，等.基于滑模变结构的永磁同步电动机调速系统设计［J］.微电机，2011，22（6）：52-56.

［9］张伦健，刘建坤，候圣语.基于滑模变结构控制的直驱永磁风力发电系统研究［J］.机电元件，2011，22（3）：15-19.

［10］刘军，王洋，黄盟芝.一种新型趋近律的滑模控制在同步电机中的应用［J］.青岛科技大学学报，2009，30（5）：457-464.［11］赵佩宏，李建林，鄂春良.变速风力机的最大风能捕获控制策略研究［J］.电气传动，2012，42（6）：3-6.

［12］Li Q，Pan Z P.The Modeling and Simulation of Brushless Doubly-fed Generator of Wind Power Generation System［J］.Power Electronics and Drive Systems，2001，2（4）：811-814.

［13］张晓光，赵克，孙力，等.永磁同步电机滑模变结构调速系统动态品质控制［J］.中国电机工程学报，2011，31（15）：47-52.