流化床内颗粒旋转特性的数值模拟
李 斌,宋小龙
(华北电力大学 能源动力与机械工程学院,保定071003)
流化床作为高效、低污染清洁燃烧技术在电力行业中得到了较为广泛的应用,但是其床内复杂的气固两相流流动行为还难以被人们充分了解.目前,关于流化床内颗粒速度、浓度分布的研究已相对成熟.由于受到不平衡力及颗粒间碰撞的作用,颗粒在床内平动的同时还会产生旋转,颗粒的旋转不仅会对自身的运动产生影响,还会对其所在的流场产生影响[1],因此颗粒旋转特性的研究作为颗粒速度和浓度等研究的深入对于全面认识气固两相流的流动特性具有重要意义.
随着研究的深入,流化床内颗粒的旋转逐渐引起人们的重视.目前,对颗粒旋转特性的研究主要通过试验研究和数值模拟方法,试验研究的关键在于如何准确测量颗粒的转速,有学者[2-4]对颗粒的旋转特性进行了试验研究,但是还需要进一步研究更精确地测量颗粒转速的方法.此外,也有学者采用硬球模型、直接蒙特卡罗法或双流体模型对流化床内颗粒的旋转特性进行了数值模拟[5-8],但是对流化床内颗粒旋转特性采用软球模型进行数值模拟的研究并未深入.
数值模拟的关键是建立正确的物理数学模型,流化床内气固两相流数值模拟的模型主要包括基于欧拉方法的双流体模型[9-10]和基于拉格朗日方法的颗粒轨道模型[11-12].笔者将基于欧拉-拉格朗日范畴的离散单元法和计算流体力学结合起来,在自行开发程序的基础上对流化床内颗粒的旋转特性进行了数值模拟,充分发挥离散单元法可以获得颗粒非常丰富的微观信息的优势,模拟得到床内气体的速度场、颗粒的速度场和平均体积分数以及颗粒平均转速的分布,分析了颗粒旋转对颗粒自身运动、流场、床层膨胀和床层空隙率的影响以及影响颗粒平均转速的因素,为全面认识和深入研究流化床内的气固两相流提供一定基础.
1 颗粒旋转机理
流化床中的颗粒在床内运动过程中主要受到以下力的作用:(1)颗粒与颗粒碰撞产生的碰撞力;(2)颗粒与壁面碰撞产生的力;(3)气体对颗粒产生的曳力;(4)颗粒自身重力.床内颗粒遇到以下情形时会发生旋转[5]:当2个颗粒发生偏心碰撞时,在接触点产生的碰撞力可分解成一个垂直于接触点与颗粒圆心连线方向的分力,该力产生转矩使颗粒发生旋转;当颗粒与壁面发生非垂直碰撞时,由颗粒与壁面间的摩擦力产生对颗粒圆心的转矩,使颗粒旋转;当颗粒在具有一定速度梯度的流场中运动时,在不平衡力的作用下也会发生旋转;此外,当一个旋转颗粒与一个非旋转颗粒发生碰撞时,在颗粒间摩擦力的作用下,也会使非旋转颗粒产生旋转.
根据文献[13],由颗粒碰撞引起的颗粒转速比由气体速度梯度引起的颗粒转速大得多,颗粒的碰撞成为引起颗粒旋转的主要因素.笔者在模型处理时只考虑由颗粒碰撞引起的颗粒旋转.
2 数学模型
将计算流体力学和基于欧拉-拉格朗日范畴的离散单元法相结合,对流化床内颗粒的旋转特性进行数值模拟.在欧拉坐标系下考察气相的运动,在拉格朗日坐标系下计算颗粒的运动,颗粒间的碰撞采用软球模型,根据牛顿第二定律建立每一个颗粒的运动方程,然后对每一个颗粒的运动方程进行求解,气固两相耦合采用牛顿第三定律.
2.1 颗粒间的碰撞力
软球模型中颗粒间的碰撞力包括弹性力和黏性阻尼力.根据物理学定律,颗粒间的碰撞力可分解为法向力fn,ij和切向力ft,ij.法向力包括法向弹性力fcn,ij和法向黏性阻尼力fdn,ij,切向 力ft,ij包括切向弹性力fct,ij和切向黏性阻尼力fdt,ij.
颗粒所受的法向力为

式中:kn为颗粒法向方向的弹性系数;Δδn为颗粒i和颗粒j之间的法向相对位移.

式中:ur为颗粒i相对颗粒j的速度矢量,ur=uiuj;ni为颗粒法向方向的单位矢量,方向由颗粒i的圆心指向接触点.
法向黏性阻尼力为

式中:ηn为颗粒法向方向的阻尼系数;un为颗粒i和颗粒j在接触点处的法向相对速度.

颗粒所受的切向弹性力为
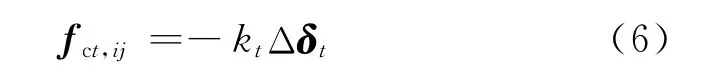
式中:kt为颗粒切向方向的弹性系数;Δδt为颗粒i和颗粒j之间的切向相对位移.

式中:ti为颗粒i切向方向的单位矢量;ωi为颗粒的旋转角速度,rad/s,规定逆时针方向为正;Ri为颗粒质心到接触点的矢量.
切向黏性阻尼力为

式中:ηt为颗粒切向方向的阻尼系数;ut为颗粒i和颗粒j在接触点的切向相对速度.
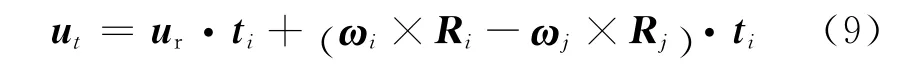
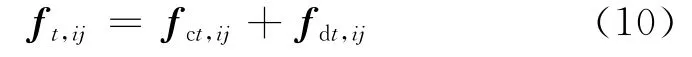
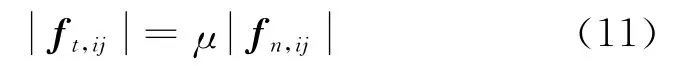
式中:μ为颗粒滑动摩擦因数.
当颗粒i与壁面发生碰撞时,将壁面看成是速度和角速度均为零的颗粒.
2.2 颗粒运动方程
颗粒在床内的运动可以分解为平动和转动.
平动运动方程为
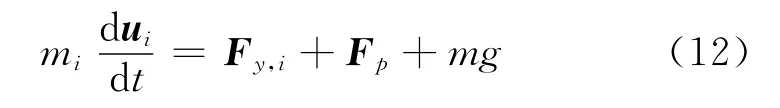
式中:Fy,i为流体对颗粒的曳力;Fp为颗粒间的碰撞力.
转动运动方程为
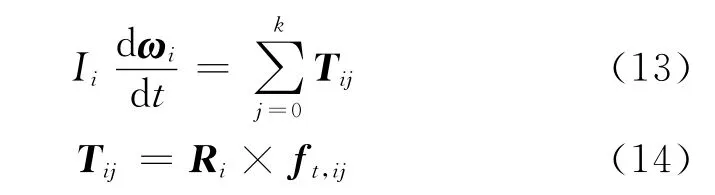
式中:Ii为颗粒i的转动惯量,对于球形颗粒Ii=2/5miR2i;Tij为颗粒i与颗粒j发生碰撞时对颗粒i产生的转矩;k为与颗粒i发生碰撞的颗粒个数.
当一个颗粒同时与周围的几个颗粒碰撞时,可以通过矢量叠加计算颗粒所受的合力及合力矩.
经过一个时间步长Δt后,颗粒i的速度、位移和角速度可由下式确定:
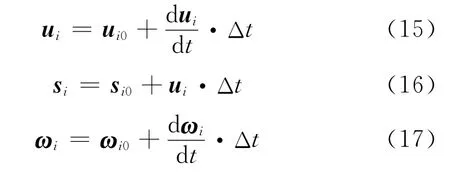
式中:ui0、si0和ωi0分别为上一时刻颗粒i的速度、位移和角速度.
2.3 气相控制方程
气相模型采用考虑气固两相耦合的Navier-Stocks方程,气相湍流模型采用k-ε两方程模型,并采用Simpler算法进行求解,详细求解模型参见文献[14]~文献[15].
2.4 模拟对象
所模拟的对象为150mm(x)×4mm(y)×900 mm(z)的矩形截面准三维流化床,床深(y方向)为颗粒直径,床层底部中心位置设置一个空气进口,空气进口宽度为10mm.计算区域的网格划分为17×1×92,水平方向(x方向)和垂直方向(z方向)的网格长度均为10mm.床料采用2 400个球形颗粒,其中颗粒的恢复系数e、弹性系数k和摩擦因数分别为0.9、200 N/m 和0.3,黏 性 系 数 采 用2×(m为等效质量)进行计算.空气密度为1.205kg/m3,动力黏度为1.8×10-5kg/(m·s).
2.5 模拟过程
首先确定床内颗粒的初始位置,方法如下:在床内随机生成2 400个颗粒位置,在只考虑重力和颗粒间碰撞力的作用下使其自由落体,颗粒最终的静止位置作为数值模拟过程中颗粒的初始位置.为了对比考虑颗粒旋转和未考虑颗粒旋转的情况,在模拟过程中将颗粒的旋转角速度随时清零,即可计算未考虑颗粒旋转的情况[5].
3 模拟结果
笔者模拟了空气进口速度为29m/s、颗粒直径为4mm 及密度为2 700kg/m3时床内颗粒的旋转特性,并对不同密度(直径均为4 mm,颗粒密度分别为3 900kg/m3、2 700kg/m3和1 500kg/m3)以及不同直径(颗粒密度均为2 700kg/m3,颗粒直径分别为3mm、4mm 和5mm)颗粒的旋转特性进行了数值模拟,得到不同密度及不同直径颗粒的平均转速分布.
3.1 流化过程图
首先模拟了空气进口速度为29m/s时考虑颗粒旋转和未考虑颗粒旋转的床内颗粒流化过程,得到加入流化气体后床内颗粒的流化过程图(图1和图2).对比图1和图2可以看出,考虑颗粒旋转后床层的膨胀高度比未考虑颗粒旋转时有所提高,且在床内更容易形成气泡.

图1 未考虑颗粒旋转的床内颗粒流化过程图Fig.1 Diagram of fluidization process without consideration of particle rotation
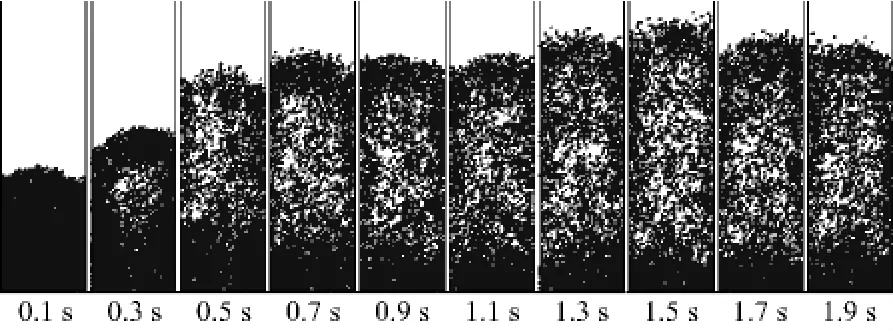
图2 考虑颗粒旋转的床内颗粒流化过程图Fig.2 Diagram of fluidization process with consideration of particle rotation
3.2 颗粒平均速度分布
图3和图4分别给出了空气进口速度为29m/s时颗粒垂直方向和水平方向平均速度的分布,其中h为床层高度(以下简称床高).从图3和图4可以看出,考虑颗粒旋转和不考虑颗粒旋转时颗粒垂直方向和水平方向的平均速度分布趋势一致.从图3还可知,在垂直方向上床层中心位置处的颗粒平均速度较大且为正值,颗粒向上运动;靠近壁面处的颗粒平均速度为负值,颗粒向下运动,从而形成流化床内颗粒环核流动,并且随床高的增加,颗粒垂直方向的平均速度减小.此外通过对比考虑颗粒旋转和不考虑颗粒旋转情况下颗粒垂直方向的平均速度可知,考虑颗粒旋转后床层中心位置处的颗粒平均速度变大,但是靠近壁面两侧的颗粒平均速度变小.从图4还可以看出,在水平方向上,靠近床层底部区域喷口中心位置左侧颗粒的平均速度为正值且向右侧运动,右侧颗粒的平均速度为负值且向左侧运动,两侧的颗粒向喷口中心位置聚集并进入主气流的喷射区,由于受到主气流的卷吸作用,该区域颗粒水平方向的平均速度较大,其他区域的颗粒分别向两侧扩散,床层表面的颗粒由于受到中间颗粒向上的排挤以及受周围颗粒的影响较小,其颗粒平均速度也较大.考虑颗粒旋转后颗粒水平方向平均速度较不考虑颗粒旋转时有所增大.

图3 颗粒垂直方向平均速度分布Fig.3 Vertical velocity distribution of particles
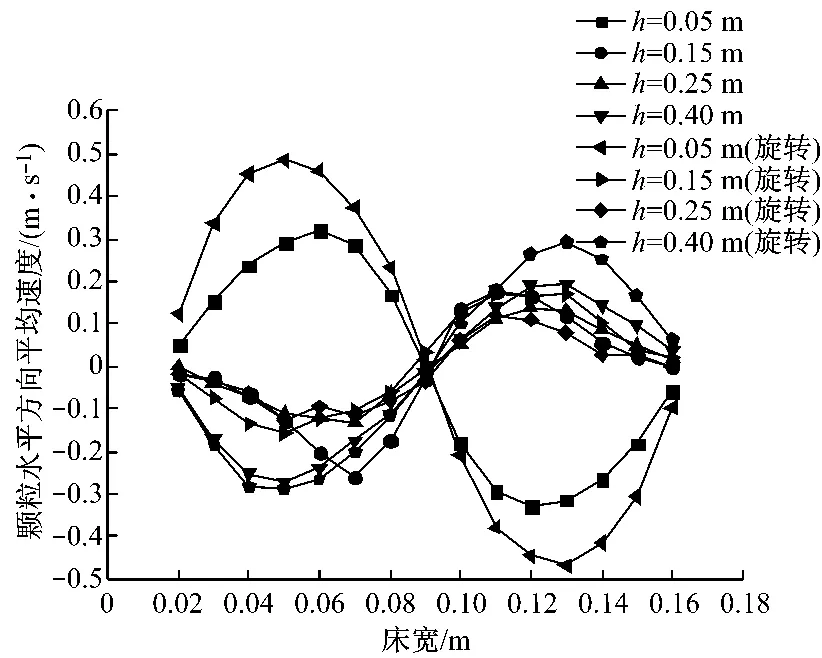
图4 颗粒水平方向平均速度分布Fig.4 Horizontal velocity distribution of particles
3.3 气体平均速度分布
图5和图6分别给出了空气进口速度为29m/s时气体垂直方向和水平方向平均速度的分布.从图5可知,垂直方向上中心位置处的气体平均速度较大且方向为正,两侧的气体平均速度较小且方向为负,并且气体平均速度随床高的增加而减小.气体水平方向平均速度以喷口为中心基本呈对称分布,喷口中心两侧的平均速度方向相反,在床层底部区域由于受主气流的卷吸作用,两侧的气体向喷口中心聚集,其他区域的气体向两侧扩散,并且随床高的增加气体水平方向平均速度减小.对比考虑颗粒旋转和不考虑颗粒旋转的情况可知,颗粒的旋转对气体水平方向平均速度的影响略大于对垂直方向平均速度的影响,但其规律并不明显.

图5 气体垂直方向平均速度分布Fig.5 Vertical velocity distribution of gas

图6 气体水平方向平均速度分布Fig.6 Horizontal velocity distribution of gas
3.4 颗粒平均体积分数分布
图7给出了考虑颗粒旋转和未考虑颗粒旋转时床内颗粒平均体积分数的分布.从图7可以看出,两种情况下颗粒平均体积分数的分布趋势相似,床内底部区域颗粒的平均体积分数较大且为浓相,上部区域颗粒的平均体积分数较小且为稀相,靠近壁面两侧的颗粒平均体积分数大于中心区域,呈现中心稀两侧密的特点.
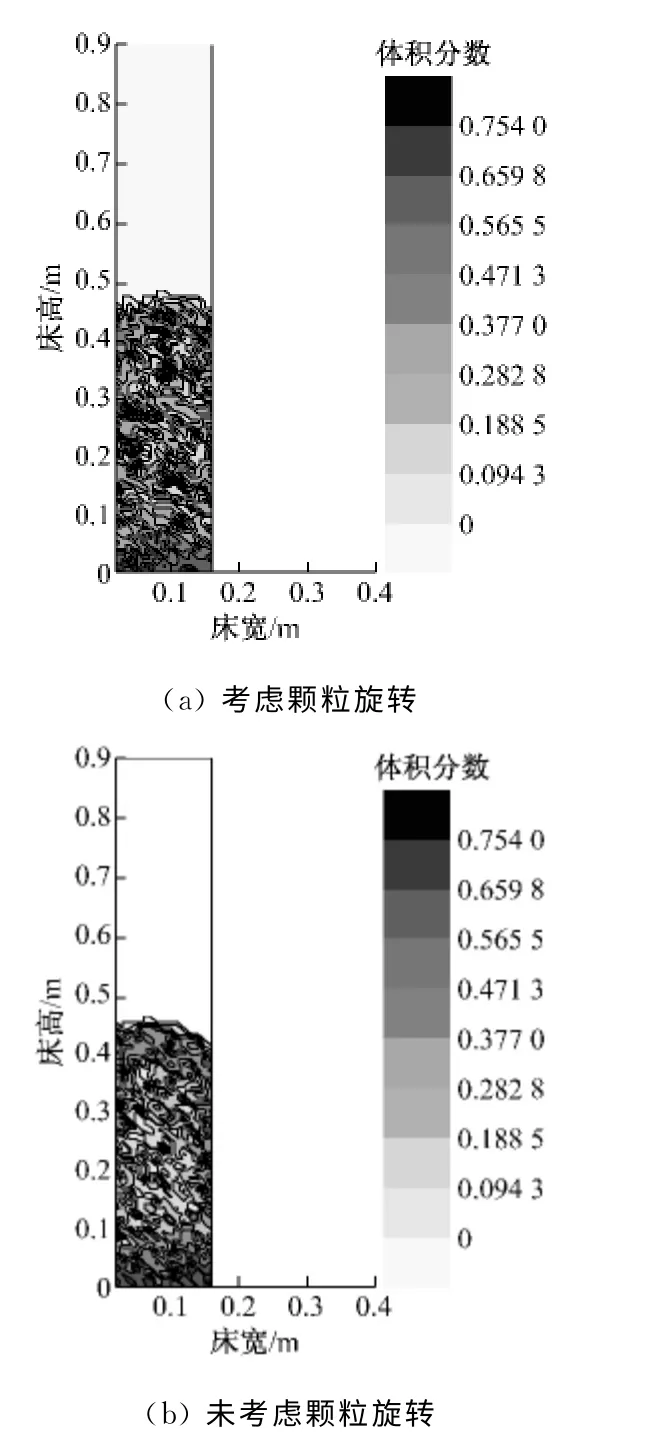
图7 颗粒平均体积分数的分布Fig.7 Distribution of average volume fraction of particles
3.5 床层平均空隙率随床高的变化趋势
图8给出了床层平均空隙率随床高的变化趋势.从图8可以看出,在床层底部考虑颗粒旋转时床层平均空隙率较未考虑颗粒旋转时有所增大,这与文献[5]采用硬球模型得到的结果基本一致,分析认为这是由于考虑颗粒旋转后床层底部区域颗粒平均速度增大的幅度较大,颗粒运动范围扩大,导致床层的平均空隙率增大.

图8 床层平均空隙率随床高的变化趋势Fig.8 Distribution of average bed void fraction along bed height
3.6 颗粒碰撞次数的分布
图9给出了0~2s内床内不同网格区域内颗粒沿床宽发生碰撞次数总和的分布趋势.从图9可以看出,颗粒的碰撞次数随着床高的增加而减小,两侧的碰撞频率略高于中心区域,这与颗粒平均体积分数的分布一致,这是由于颗粒平均体积分数较大区域的颗粒碰撞概率较高,颗粒碰撞次数增加.
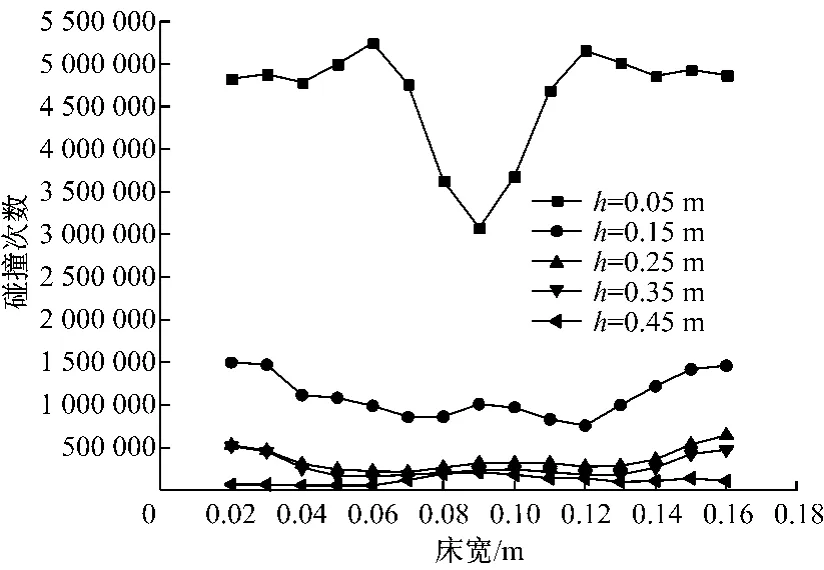
图9 考虑颗粒旋转时颗粒的碰撞次数Fig.9 Distribution of collision frequency with consideration of particle rotation
3.7 颗粒平均转速的分布
图10给出了不同床高处颗粒平均转速沿床宽的分布情况.从图10可以看出,床内喷口中心左侧颗粒的平均转速为正值,颗粒逆时针旋转;右侧颗粒的平均转速为负值,颗粒顺时针旋转,颗粒的平均转速分布与颗粒水平方向的平均速度分布趋势基本一致,水平方向平均速度较大颗粒的平均转速也较大,这是由于水平方向平均速度大的颗粒与其他颗粒和壁面的碰撞概率增加,颗粒经历的流场相对复杂,从而增加了颗粒增大平均转速的机会[3].随着床高的增加,颗粒平均转速减小,这与颗粒碰撞次数的分布相吻合,但靠近壁面处颗粒的平均转速小于两侧中心区域,分析认为这是由于颗粒的平均转速不仅与碰撞次数有关,还与颗粒间的碰撞强度有关,虽然靠近壁面处的颗粒体积分数较大,碰撞次数较多,但是靠近壁面处颗粒的平均速度较小,颗粒碰撞强度较弱,因此颗粒的平均转速相对较小.从图10还可以看出,颗粒平均转速与颗粒垂直方向平均速度的关系不大.

图10 颗粒平均转速的分布Fig.10 Average rotating speed distribution of particles
3.8 不同密度颗粒的平均转速随床宽的变化趋势
图11给出了空气进口速度为29 m/s、颗粒直径均为4mm 时不同密度颗粒的平均转速随床宽的变化.从图11可以看出,密度较大的颗粒的平均转速小于密度较小的颗粒,这是由于密度较大的颗粒转动惯量较大,在受到相同转矩时,颗粒的角加速度较小,因而颗粒角速度和平均转速较小.
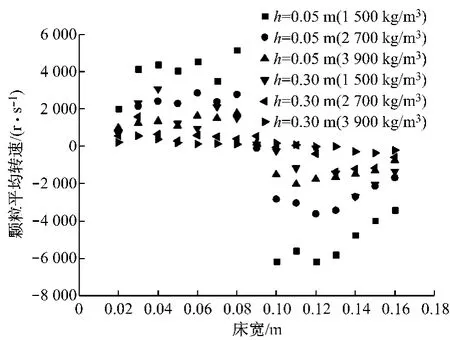
图11 不同密度颗粒的平均转速随床宽的变化趋势Fig.11 Distribution of average rotating speed along bed width for particles of different densities
3.9 不同直径颗粒的平均转速随床宽的变化趋势
图12给出了空气进口速度为29 m/s、颗粒密度均为2 700kg/m3时不同直径颗粒的平均转速随床宽的变化.从图12可知,直径小的颗粒平均转速大于直径大的颗粒,这与文献[3]的结果一致,这是由于在受到相同转矩时,直径较小的颗粒转动惯量较小,因而可以获得更大的平均转速.

图12 不同直径颗粒的平均转速随床宽的变化Fig.12 Distribution of average rotating speed along bed width for particles of different sizes
4 结 论
(1)考虑颗粒旋转和未考虑颗粒旋转时模拟得到的气体速度场、颗粒速度场和平均体积分数的分布趋势基本一致.
(2)考虑颗粒旋转后,在垂直方向上床层中心位置处的颗粒平均速度增大,靠近壁面两侧的颗粒平均速度减小,颗粒水平方向的平均速度较未考虑颗粒旋转时有所增大.
(3)与未考虑颗粒旋转情况相比,考虑颗粒旋转后床层膨胀高度有所增加,底部区域的床层平均空隙率增大.
(4)颗粒间的碰撞次数与床内颗粒平均体积分数分布趋势一致,颗粒碰撞次数随着床高增加而减小,靠近壁面两侧的颗粒碰撞频率略高于中心区域.
(5)床内喷口中心左侧的颗粒逆时针旋转,右侧的颗粒顺时针旋转,且颗粒的平均转速随床高的增加而减小,颗粒平均转速的分布与颗粒水平方向平均速度的分布趋势基本一致.
(6)颗粒的平均转速不仅与颗粒间的碰撞次数有关,还与颗粒间的碰撞强度有关,并且密度大的颗粒的平均转速相对较小,密度小的颗粒的平均转速相对较大,直径小的颗粒的平均转速大于直径大的颗粒.
[1]由长福,祁海鹰,徐旭常.煤粉颗粒所受Magnus力的数值模拟[J].工程热物理学报,2001,22(5):625-628. YOU Changfu,QI Haiying,XU Xuchang.Numerical simulation of Magnus lift on a coal particle[J].Journal of Engineering Thermophysics,2001,22(5):625-628.
[2]吴学成,王勤辉,骆仲泱,等.高速数字摄影应用于流化床内颗粒旋转特性的测试[J].中国电机工程学报,2005,25(17):72-77. WU Xuecheng,WANG Qinhui,LUO Zhongyang,et al.Measurement of particle rotation in CFB riser with high-speed digital video camera techique[J].Proceedings of the CSEE,2005,25(17):72-77.
[3]骆仲泱,吴学成,王勤辉,等.循环流化床中颗粒旋转特性[J].化工学报,2005,25(10):1869-1874. LUO Zhongyang,WU Xuecheng,WANG Qinhui,et al.Particle rotation characteristics in CFB riser[J].Journal of Chemical Industry and Engineering(China),2005,25(10):1869-1874.
[4]高琼.循环流化床内部颗粒流动特性的试验研究[D].杭州:浙江大学,2005.
[5]袁竹林,马明,徐益谦,等.离散数值模拟颗粒自转对流化床内颗粒流态的影响[J].燃烧科学与技术,2001,7(3):238-241. YUAN Zhulin,MA Ming,XU Yiqian,etal.Study on effect of particle rotation on fluidizing behavior using discrete numerical simulation method[J].Journal of Combustion Science and Technology,2001,7(3):238-241.
[6]郝振华,陈巨辉,白颖华,等.考虑颗粒旋转的颗粒动力学模拟提升管气固两相流动特性[J].高校化学工程学报,2010,24(5):776-782. HAO Zhenhua,CHEN Juhui,BAI Yinghua,etal.Numerical study on gas-solid flow in a riser using dynamic theory with consideration of particle rotation[J].Journal of Chemical Engineering of Chinese Universities,2010,24(5):776-782.
[7]SUN J,BATTAGLIA F.Hydrodynamic modeling of particle rotation for segregation in bubbling gas-fluidized beds[J].Chemical Engineering Science,2006,61(5):1470-1479.
[8]TRIESCH O,BOHNET M.Measurement and CFD prediction of velocity and concentration profiles in a decelerated gas-solids flow[J].Powder Technology,2001,115(2):101-113.
[9]HUILIN L,GIDASPOW D.Hydrodynamics of binary fluidization in a riser:CFD simulation using two granular temperatures[J].Chemical Engineering Science,2003,58(16):3777-3792.
[10]HUILIN L,YURONG H,GIDASPOW D.Hydrodynamic modelling of binary mixture in a gas bubbling fluidized bed using the kinetic theory of granular flow[J].Chemical Engineering Science,2003,58(7):1197-1205.
[11]XU B H,YU A B.Numerical simulation of the gassolid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics[J].Chemical Engineering Science,1997,52(16):2785-2809.
[12]田凤国,章明川,顾明言,等.流化床微观混合过程的定量评价[J].动力工程,2007,27(1):45-49. TIAN Fengguo,ZHANG Mingchuan,GU Mingyan,etal.Quantitative evaluation of micro-mixing processes in fluidized beds[J].Journal of Power Engineering,2007,27(1):45-49.
[13]WU X,WANG Q,LUO Z,etal.Theoretical and experimental investigations on particle rotation speed in CFB riser[J].Chemical Engineering Science,2008,63(15):3979-3987.
[14]李斌,纪律.流化床炉内颗粒混合的离散单元法数值模拟[J].中国电机工程学报,2012,32(20):42-48. LI Bin,JI Lü.Numerical simulation of particle mixing in circulating fluidized bed with discrete element method[J].Proceedings of the CSEE,2012,32(20):42-48.
[15]纪律.循环流化床流动及磨损特性的DEM 数值模拟[D].保定:华北电力大学,2011.

