新型3D⁃Turbo码原理分析与性能研究

姚如贵，高凡琪，张 昆，徐 娟

（1.西北工业大学电子信息学院，710072西安；2.长安大学电控学院，710064西安）

新型3D⁃Turbo码原理分析与性能研究

姚如贵1，高凡琪1，张 昆1，徐 娟2

（1.西北工业大学电子信息学院，710072西安；2.长安大学电控学院，710064西安）

为改善中高信噪比下传统Turbo的错误平台性能，介绍一种改进的Turbo码（3D⁃Turbo Codes），通过增加一个码率为1的后编码器，对传统Turbo编码器得到的部分校验比特进行后编码.给出3D⁃Turbo码的编码结构，分析了影响性能的主要因素，研究3D⁃Turbo码的迭代译码过程并详细推导了Max⁃Log-Map算法，最后对3GPP2标准下的3D⁃Turbo码性能进行仿真.研究结果表明，与3GPP2 Turbo码相比，3D⁃Turbo码通过增加很小的复杂度，可以有效改善错误平台性能.因此，在中高信噪比且对误码率要求严格的场景下，3D⁃Turbo码有广阔的应用空间.

3D⁃Turbo码；3GPP2；错误平台；收敛特性

Turbo码是最接近香农极限的信道编码方式之一［1］.Turbo码可以达到距离香农极限0.7 dB的优异性能，因此被应用到通信系统的很多领域［2］.Turbo码的误码率曲线在瀑布区有着优异的收敛性能，但是由于最小汉明距离（MHD）相对较小，导致在中高信噪比条件下，BER曲线变得平坦，出现错误平台.

改善高信噪比时的误码性能，需要增加最小汉明距离.通常用以下3种方式来实现：使用具有更多状态的成员编码器，设计更复杂的内交织器，或者增加Turbo码的维数.文献［3］提出了一种基于16状态子编码器的Turbo码，误帧率（FER）可以到达10-7.但是，在实现时间和存储复杂度上，几乎是8状态Turbo码的2倍.文献［4］提出DRP交织器能够得到更大的最小汉明距离.但是，复杂交织器一般不具备良好的结构特征，在工程实现时需要耗费大量存储资源.传统多维Turbo码增加并联成员编码器个数并不能有效改善错误平台特性［5-6］.基于此本文介绍一种新型3D⁃Turbo码［7］，采用混联结构，在传统Turbo码编码器的输出端添加一个码率为1的后编码器，抽取部分校验比特进行二次编码.相比于传统Turbo码，3D⁃Turbo码通过增加很小的译码复杂度和译码延迟，有效地改善了错误平台的性能.3D⁃Turbo码有广阔的工程实现前景，适用于一些对译码延迟不敏感，但对误码比较敏感的应用场景.例如，在深空通信中，采集的信息都十分珍贵，希望采集信息损失尽可能的小，在中高信噪比条件下，要求获得极低的误码率.

关于3D⁃Turbo码性能及优化研究［7-9］，均为ENST Bretagne学院Berrou团队发表，但是现有文献中对于译码算法中关键推导（如校验比特先验信息的使用、校验信息外信息的计算等）未给出，同时实现过程中关键模块（如抽取、译码信息传递等）也未进行明确说明.本文结合课题组研究结论，对上述关键推导和关键模块进行详细阐述.

1 3D⁃Turbo码编码结构

图1所示为基于3GPP2标准3D⁃Turbo码编码原理框图.虚线框所示部分为传统的Turbo码编码器，包括1个内交织器π和2个并行的分量编码器.分量编码器为8状态递归系统卷积码（RSC），生成多项式为（15，13）8.长度为K的信息序列U分为3路．第1路直接输出作为编码后的系统比特，用X来表示；第2路送到分量编码器1中进行编码产生校验比特，用Y1表示；第3路经过交织器π交织后送到分量编码器2中进行编码，产生校验比特Y2．编码后码字由系统比特X和校验比特Y1和Y2组成，码率R＝1／3．

图1 3D⁃Turbo码原理框图

3D⁃Turbo码是在传统的混联方式上发展而来.通过增加并串转换模块、后交织器π′和一个码率为1的后编码器，来实现对部分校验比特的后编码.通过后编码，可以有效减少码重较小的码字，以此提高整体码字的MHD［8］.

从校验比特Y1和Y2中，按照一定的比例和模式抽取部分比特，经过并串转换后，组成新的编码序列P，经π′交织后，送到码率为1的后编码器，进行二次编码．未被抽取的校验比特不需要进行后编码，直接送到删截器．用λ（0≤λ≤1）表示抽取率，即参与后编码的校验比特在总校验比特中所占的比例．为便于实现，一般采用规则的抽取方式．以λ＝1／4为例，对校验比特序列Y1、Y2，每4个比特抽取1个，组成帧送到后编码器中进行编码．抽取方式如图2所示．

图2 校验比特抽取示意

可看出，送到后编码器的校验比特个数可用L＝2λK来表示．剩余的未被抽取的2（1-λ）K个校验比特，与后编码器输出的校验比特一起送到删截器中．一般情况下，后编码器产生的校验比特含有更多的信息，尽量不做删除．

2 影响性能的因素

3D⁃Turbo码中，除了传统的码长、码率、生成多项式等因素影响性能外，渗透率、后编码器的生成多项式和交织器同样对性能的影响很大.

2.1 渗透率λ

渗透率λ的选择能够平衡译码器的收敛性能和错误平台性能.收敛性表征了译码性能从高误码率到低误码率变化的快慢.抽取校验比特的译码涉及到主译码器和预译码器之间的外信息传递，因此会出现错误传递现象.在低信噪比下校验比特出现错误的概率更大，所以错误传递在低信噪比下尤其突出.进一步反映在译码性能上时，就是在低信噪比的情况下，3D⁃Turbo码的收敛性能降低.因此，选择较大的λ值，可以获得更低的错误平台性能，但是译码器的收敛性却会降低.反之，选择较小的λ值，译码的收敛性能有所改善，但是错误平台较高［7］.

2.2 后编码器

后编码器对3D⁃Turbo码的性能有着极大的影响.后编码器的选取要综合考虑实现复杂度和性能两方面.首先，对应的预译码器结构必须简单，相比传统Turbo码，在软输入软输出（SISO）译码时，不能增加太多的实现复杂度.其次，考虑到第一次迭代译码时，没有可以利用的先验信息，所以对应的预译码器不能引入太多错误符号，避免降低收敛性能.综上，后编码器可以选择状态数较少的循环递归系统卷积码（CRSC）.文献［8］推荐了一种带有两个寄存器的线性编码器，后编码器的生成多项式为（5，4）8.

2.3 交织器π和π′

在设计Turbo码交织器时需要综合考虑两方面，一方面需要使Turbo码的距离特性得到最优化，提高纠错性能；另一方面需要考虑译码器的实现复杂度.3D⁃Turbo码中有两个交织器，一是传统Turbo码中的交织器π，本文中选择3GPP2标准中的内交织方案.另一个是后编码器部分的后交织器π′．交织器的性能是影响其译码性能的关键因素之一．后交织器π′的功能是将编码序列P进行交织，目的是为了防止预译码器译码时出现连续的错误，影响总体译码的性能．文献［7］给出一个π′的规则交织方式，具有简单的结构和良好的性能．设交织器π′的交织长度为L，i（1≤i≤L）和j（1≤j≤L）分别是自然顺序和交织后顺序的地址．π′可以用下列关系式表示：

式中i0是初始参数，且L0和L互质．

3 3D⁃Turbo码译码

3.1 译码过程

3D⁃Turbo码的译码原理与传统Turbo码相似，都是通过成员译码器之间互相传递互信息，来进行迭代译码.3D⁃Turbo码译码器由3个成员译码器构成，分别是4状态的SISO预译码器和两个分量译码器，译码原理框图如图3所示.

图3 3D⁃Turbo码译码器原理框图

假设参与后编码的输出比特W经过信道传输后为Wch．3D⁃Turbo码的译码迭代过程为：首次迭代时，预译码器开始工作.校验比特的先验信息初始化为0，此时预译码器仅利用接收到的信道信息Wch进行译码.将预译码器产生的外信息作为校验比特的先验信息送到主译码器中.主译码器利用信道信息和预译码器产生的外信息，进行第一次迭代译码.主译码器的两个分量译码器同传统的Turbo码译码器相同，产生关于系统比特的外信息，并作为先验信息相互交换.同时，主译码器还为预译码器提供关于后编码校验比特的外信息（可由式（16）计算）.之后的迭代过程中，预译码器和主译码器之间传递关于抽取校验比特的外信息，主译码器内部的分量译码器之间传递关于系统比特的外信息.当所有的分量译码器收敛或者最大的迭代次数完成时，停止迭代过程.

3.2 Max-Log-Map算法推导

由于后编码器的引入，3D⁃Turbo码主译码器的译码算法与传统的Turbo码相比略有不同.主要区别如下：在计算分支度量时，引入了关于校验比特的先验信息；计算对数似然比时，需要考虑关于校验比特的先验信息；需要输出关于校验比特的外信息.

基于BCJR算法［12］，本文详细推导了3D⁃Turbo码Max-Log-Map译码算法，推导过程也可以推广到Log-Map算法.下面分别给出主译码器和预译码器译码算法的推导过程.

1）主译码器

编码器的M个不同状态记为m（m＝0，1，…，M-1）．时刻t的状态为St，对应输出为，接收符号为．时刻t到t′的状态序列为，对应的输出序列为，接收序列为｛Y1，…，Yτ｝．信道为AWGN，噪声方差为σ2．

译码器通过检测接收序列Yτ1来预测马尔可夫过程的状态概率（式（2））和状态转移概率（式（3））．

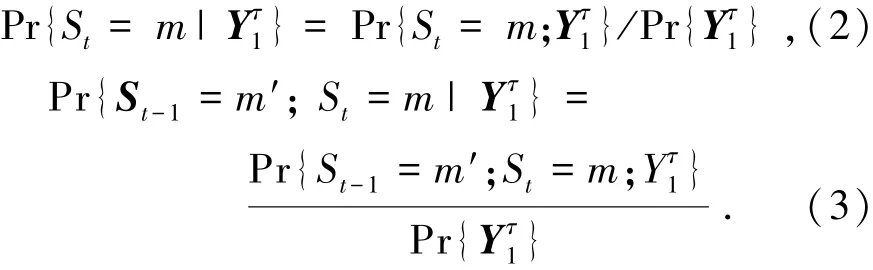
依据传统Turbo码算法，α和β可递归计算为

其递推关系可以进一步如图4表示.

图4 前向和后向路径度量的计算示意

从状态St-1→St，代表状态转移格图中的一条边，在3D⁃Turbo码中，主译码器既获得了系统比特的先验信息，也获得了校验比特的先验信息，所以状态转移概率可以同时利用系统比特和校验比特来表示.

先验信息Le（ut）＝ln（Pr｛ut＝＋1｝／Pr｛ut＝-1｝），所以ut的先验概率计算为

同理可得校验位χpt的先验概率为

由于信道的高斯随机过程特性，可以得到式（11），其中，A是一个取值与ut和取值无关的值．

定义信道置信因子Lc＝4Es／N0＝2／σ2，结合式（8）～（11），同时忽略共同项可得：

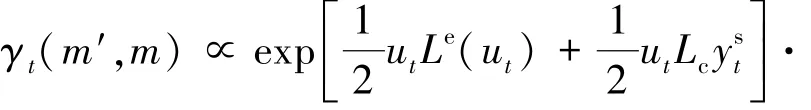
令At（m）＝ln αt（m），Bt（m）＝ln βt（m），Mt（m′，m）＝ln γt（m′，m），则可以得到MAP算法的对数域形式．为简化指数运算，Log-Map算法中引入max∗（χ，y）＝ln（eχ＋ey）＝max（χ，y）＋fc（｜χ-y｜），其中fc（χ）＝ln（1＋e-χ）为修正项．令fc（χ）＝0，则max∗（χ，y）可以进一步简化为max（χ，y），从而：

根据对数似然比定义，以及式（3）、（5），关于系统比特的对数似然比计算如下：

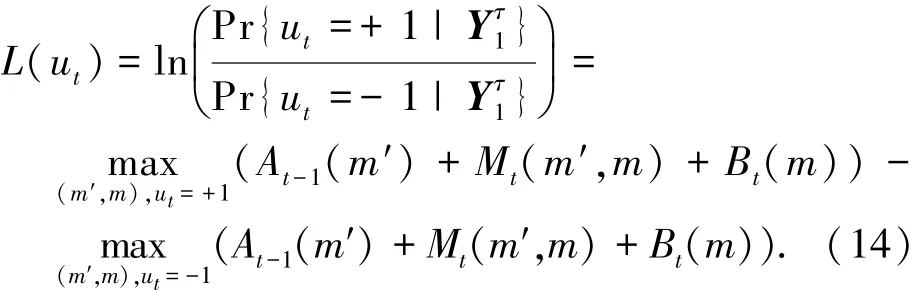
结合式（12）、（14），L（ut）还可以表示为如下形式，表征了对数似然比、系统信息、先验信息及外信息之间的关系．

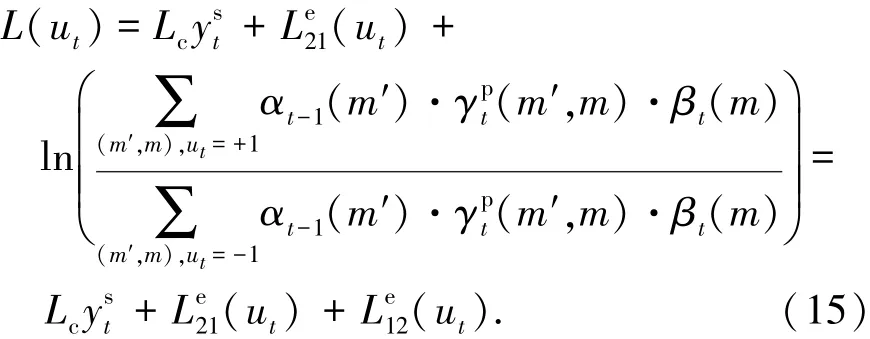
当上述关于分支度量、前向路径度量、后向路径度量和对数似然比的计算中采用max∗（χ，y）代替max（χ，y），即可获得Log-Map算法.

2）预译码器

因为后编码器是码率为1的编码器，即编码后码字只有校验比特，没有系统比特，所以对应预译码器的Max-Log-Map译码算法公式也与主译码器略有不同.分支度量计算为

式中：wt为进行后编码的校验比特，即为后编码器的输入；（wt）为主译码器经过π′交织后传给预译码器的先验信息．为后编码器产生的校验位，为对应的信道信息．关于前向路径度量和后向路径度量计算方法同主译码器．同理，后编码器关于校验比特外信息的计算公式为

由于后编码器没有输出系统信息，因此，上式中没有与系统信息对应的Lc归一化的信道输入.

3.3 复杂度与时延分析

由3.2节推导可知，与传统的Turbo码译码器相比，增加的复杂度主要来自预译码器和主译码器中计算关于后编码输入校验比特的外信息.表1给出了采用Max-Log-Map算法时，3D⁃Turbo码译码器对每比特译码额外增加的计算量统计.其中v和w分别为主编码器和后编码器的移位寄存器长度，主译码器中分量编码器输出n路．由表1可以看出，由于后编码器的存储深度w较小，因此复杂度增加不大．λ越大，预译码器需要计算的校验比特外信息的长度越大，复杂度相应的增加．另外，引入交织器π′的也会带来一定的复杂度，主要体现在交织图样的计算上.

表1 译码器计算量比较

3D⁃Turbo码的译码时延增加主要体现在计算校验比特的外信息上.在主译码器中，校验比特和信息比特的外信息可以并行计算，所以不需要消耗额外的时钟.在预译码器中，计算时延与参与后编码的校验比特的长度有关.如果主译码器的分量译码器译码时延为T，则预译码器的时延可以表示为2λT，整个时延为2（1＋λ）T．当λ＝1／4时，相对传统Turbo码时延增加25%.基于并行快速Turbo码译码算法的思路，若采用主译码器和预译码器并行运算，此时，3D⁃Turbo码的译码时延完全和传统Turbo译码器相同.而且可以预期这种并行算法对性能影响可以忽略不计.将在后续工作中进一步研究快速译码算法及其硬件实现方案.

4 仿真结果分析

本节评估3D⁃Turbo码在AWGN信道、BPSK调制时的性能，RSN为比特信噪比.3GPP2 Turbo码和3D⁃Turbo码的码长K＝570，码率R＝1／3，主编码器的生成多项式为（15，13）8，内交织器π参照3GPP2标准中的规则交织进行设计［13］. 3D⁃Turbo码的交织器π′按2.3节所述方案设计，其中，参数L0＝7，i0＝1．

3GPP2 Turbo码和3D⁃Turbo码的性能比较如图5所示，译码算法选择为Max-Log-Map算法，迭代次数设置为10.其中3D⁃Turbo码的渗透率λ＝1／4，后编码器的生成多项式为（5，4）8.

图5 3GPP2 Turbo码和3D⁃Turbo码性能比较

由图5中关于BER和FER的比较，在低信噪比的情况下，3GPP2 Turbo码的性能要好于3D⁃Turbo码.但是随着信噪比的增加（约为2.7 dB时），3GPP2 Turbo码出现错误平台，而3D⁃Turbo码仍然处于瀑布区，可以预计获得更低的错误平台.

图6显示了不同渗透率或者编码器结构对应的3D⁃Turbo码的性能.译码算法选择为Max-Log-Map算法，迭代次数设置为10.对比图6中的曲线差异，可以看出，当渗透率λ＝1／4时，3D⁃Turbo码在低信噪比下性能要略差于λ＝1／8对应的误码性能，但是可以获得更低的错误平台．这是因为较大的渗透率会得到更高的MHD，会使得错误平层更低［7］.后编码器的生成多项式为（5，4）8时，当第一次迭代时，产生的错误符号要少于后编码为（7，4）8产生的错误符号［8］，错误传递导致后者的误码性能较差.

图6 不同渗透率和后编码器结构对应的3D⁃Turbo码性能

图7 显示了不同译码算法下的3D⁃Turbo码的性能对比.迭代次数设置为10，渗透率λ＝1／4，后编码器的生成多项式为（5，4）8.对比图7中性能曲线的差异，在相同仿真条件下，Max-Log-Map算法的译码性能比Log-Map算法的译码性能要差，大约有0.3 dB的性能损失，这与传统Turbo码对应的结论一致.

图7 3D⁃Turbo码不同译码算法性能对比

5 结 语

为了获得比传统Turbo码更低错误平台，本文研究了一种改进的Turbo码—3D⁃Turbo码. 3D⁃Turbo码是在混合级联码的基础上发展的，综合了并行和串行级联码的优点.介绍了3D⁃Turbo码的编码结构，并详细推导了译码算法，具体分析了3D⁃Turbo码实现时的关键技术.仿真结果证明了3D⁃Turbo码的性能及其可行性，相比于传统的Turbo码，3D⁃Turbo码在高信噪比下，可以获得更低的错误平台.但是，由于后编码器、预译码器以及交织器π′的引入，增加了一些复杂度和时延.考虑到深空通信等应用场景，以少量的复杂度增加和相对传播时延较小的译码时延，可以获得极低的误码率，具有十分重要的工程应用价值.

［1］BERROU C，GLAVIEUX A，THITIMAJSHIMA P.Near shannon limit error⁃correcting coding and decoding：turbo⁃codes［C］／／ProceedingsofInternational Conference on Communications（ICC’93）.Geneva：IEEE，1993：1064-1070.

［2］王视环.LTE中Turbo码内部交织器的研究［J］.南京邮电大学学报，2010，30（4）：90-94.

［3］DOUILLARD C，BERROU C.Turbo codes with rate-m／（m＋1）constituent convolutional codes［J］.IEEE Transactions on Communications，2005，53（10）：1630-1638.

［4］CROZIER S，GUINAND P.High⁃performance low⁃memory interleaver banks for turbo⁃codes［C］／／Proceedings of 54th IEEE Vehicle Technology Conference（VTC’01）. Atlantic City：IEEE，2001：2394-2398.

［5］白宝明，马啸，刘丰，等.三维Turbo码的设计与性能分析［J］.西安电子科技大学学报，1998，25（5）：570-574.

［6］赵曾珠，张兴周，贾红轶.三维Turbo码性能的研究［J］.应用科技，2006，33（5）：12-13.

［7］BERROU C，GRAELL I AMAT A，OUID CHEIKH MOUHAMEDOU Y，et al.Adding a rate-1 third dimension to turbo codes［C］／／Proceedings of IEEE InformationTheoryWorkshop.TahoeCity：IEEE，2007：156-161.

［8］BERROU C，GRAELL I AMAT A，OUID CHEIKH MOUHAMEDOU Y，et al.Improving the distance properties of turbo codes using a third component code：3Dturbocodes［J］.IEEETransactionson Communications，2009，57（9）：2505-2509.

［9］ROSNES E，GRAELL I AMAT A.Performance analysis of 3-D turbo codes［J］.IEEE Transactions on Information Theory，2011，57（6）：3707-3720.

［10］KBAIER BEN ISMAIL D，DOUILLARD C，KEROUEDAN S. Analysis of 3⁃dimensional turbo codes［J］.Annual Telecommunications，2011，65（7）：257-268.

［11］KBAIER BEN ISMAIL D，DOUILLARD C，KEROUEDAN S. A survey of three⁃dimensional turbo codes and recent performance enhancements［J］.EURASIP Journal on Wireless Communications and Networking，2013，2013（115）：1-13.

［12］BAHL L，COCKE J，JELINEK F，et al.Optimal decoding of linear codes for minimizing symbol error rate［J］. IEEE Transactions on Information Theory，1974，20（2）：284-287.

［13］3GPP2，C.S0002⁃F.Physical layer standard for cdma2000 spread spectrum systems［S］.Seattle：Third Generation Partnership Project 2（3GPP2），2012：184-192.

（编辑 苗秀芝）

Theoretical analysis and performance study of 3-dimension Turbo codes

YAO Rugui1，GAO Fanqi1，ZHANG Kun1，XU Juan2

（1.School of Electronics and Information，Northwestern Polytechnical University，710072 Xi′an，China；2.School of Electronic and Control Engineering，Chang＇an University，710064 Xi′an，China）

In order to prevent high error floor of classic Turbo at middle and high SNRs，a modified Turbo codes，named as 3D⁃Turbo codes，is proposed in which some of the parity bits from the classical encoders are further encoded by a rate-1 post encoder.The encoder structure of 3D⁃Turbo Codes is introduced and analysis of main factors affecting performance is provided，then the iterative decoding process and detailed derivation of the Max-Log-Map algorithm of 3D⁃Turbo Codes is presented，performance based on 3GPP2 standards is simulated.The theoretical analysis and results show that 3D⁃Turbo Codes have lower error floor compared to 3GPP2 Turbo Codes，at the expense of a very small increase in complexity.Therefore，under middle or high SNRs and strict BER requirement，3D⁃Turbo Codes are expected to have extensive application prospects.

3D⁃Turbo Codes；3GPP2；error floor；convergence performance

TN911.2

：A

：0367-6234（2014）11-0095-06

2014-01-14.

国家高技术研究发展计划（2012AA120604）；航天支撑基金（2013-HT-XGD）；西北工业大学基础研究基金（JCY20130132）.

姚如贵（1980—），男，副教授.

姚如贵，yaorg＠nwpu.edu.cn.